Преобразование Звезда-Треугольник: схемы и расчет

Содержание страницы

1. Эквивалентная замена соединений обмоток источника питания
2. Эквивалентная замена соединений приемника (нагрузки)
3. Составление эквивалентных схем на одну фазу
4. Сравнительная таблица соединений
5. Преимущества и недостатки метода преобразования
6. Интересныех факты о трехфазных цепях
7. FAQ: Часто задаваемые вопросы
Заключение

Преобразование «звезда-треугольник» (и обратное ему) — это фундаментальный метод упрощения сложных электрических схем, который позволяет заменить три ветви, соединенные в общий узел (звезда), на три ветви, образующие замкнутый контур (треугольник), без изменения потенциалов узлов и токов во внешней цепи.

Историческая справка: Теоретическое обоснование этого метода было дано в конце XIX века. В 1899 году А.Е. Кеннелли доказал теорему о возможности замены звезды на треугольник. Однако практическое применение метода в трехфазных цепях тесно связано с именем Михаила Осиповича Доливо-Добровольского, который в 1880-90-х годах разработал все основные элементы трехфазных систем, включая генераторы и трансформаторы с различными типами обмоток.

Аналогия: Представьте сложную дорожную развязку. Соединение «Звезда» похоже на перекресток, где три дороги сходятся в одной центральной точке (нейтраль). Соединение «Треугольник» напоминает кольцевую дорогу, соединяющую три города напрямую друг с другом. Метод преобразования позволяет математически «перестроить» перекресток в кольцо (и наоборот), чтобы рассчитать пропускную способность трассы, не меняя при этом количество машин, въезжающих и выезжающих из этой зоны.

1. Эквивалентная замена соединений обмоток источника питания

На практике к одному трехфазному источнику энергии часто подключается группа различных приемников. Поскольку схемы соединения фаз источников и приемников могут различаться, для корректного расчета режима работы цепи применяют метод взаимного преобразования топологий.

При анализе трехфазных цепей инженеры часто сталкиваются с ситуацией, когда тип соединения обмоток генератора или трансформатора явно не указан. Для упрощения вычислений, особенно в случае симметричного источника, принято использовать эквивалентную схему замещения «Звезда».

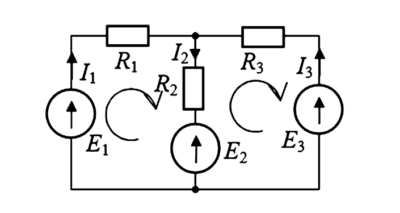
В силу свойств симметрии, схема, где обмотки источника собраны в треугольник, может быть математически заменена на эквивалентную схему «Звезда» относительно выходных клемм A, B, C (см. Рисунок 1). Это значительно облегчает расчет токов.

На рисунке слева показан источник, соединенный треугольником с ЭДС \( E_{AB} \), \( E_{BC} \), \( E_{CA} \). Справа показана его эквивалентная схема замещения звездой с фазными ЭДС \( E_A \), \( E_B \), \( E_C \) и нейтральной точкой.

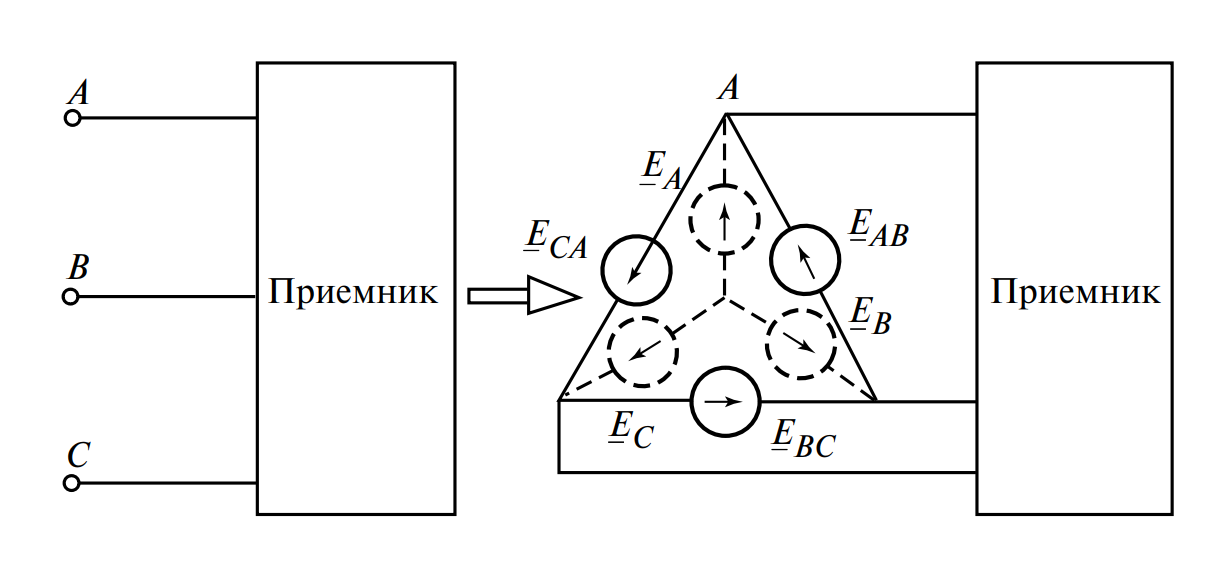
Рис. 1. Эквивалентная замена соединений обмоток источника

При таком переходе фазные ЭДС эквивалентной звезды \( E_A, E_B, E_C \) связаны с линейными ЭДС исходного треугольника \( E_{AB}, E_{BC}, E_{CA} \) следующим соотношением:

E_{AB} = E_A \cdot \sqrt{3}

Важно отметить, что положительные направления ЭДС при соединении треугольником традиционно принимаются против часовой стрелки.

В симметричной трехпроводной системе эквивалентная схема выбирается исключительно из соображений удобства вычислений. Выбранная модель не зависит от того, как физически соединены обмотки реального генератора «под крышкой». Главное — чтобы на зажимах напряжение было идентичным.

2. Эквивалентная замена соединений приемника (нагрузки)

Фазы потребителей электроэнергии также могут коммутироваться по схеме «Звезда» (Рис. 2, а) или «Треугольник» (Рис. 2, б).
Слева (а) показана схема соединения сопротивлений нагрузки \( Z_a \), \( Z_b \), \( Z_c \) в звезду с нейтральной точкой \( n \). Справа (б) показана схема соединения сопротивлений \( Z_{ab} \), \( Z_{bc} \), \( Z_{ca} \) в треугольник. Также на схемах могут быть обозначены сопротивления линий \( Z_л \).

Рис. 2. Варианты соединения фаз приемника: а) Звезда; б) Треугольник

Преобразование «Треугольник» в «Звезду»

Частая задача: дана схема с нагрузкой в виде треугольника (Рис. 2, б), но необходимо учесть сопротивление подводящих проводов \( Z_л \). В исходном виде это сделать сложно. Удобнее заменить треугольник сопротивлений \( Z_{ab}, Z_{bc}, Z_{ca} \) на эквивалентную звезду \( Z_a, Z_b, Z_c \).

Формулы для расчета сопротивлений лучей новой звезды выглядят следующим образом:

Z_a = \frac{Z_{ab} \cdot Z_{ca}}{Z_{ab} + Z_{bc} + Z_{ca}} \] \[ Z_b = \frac{Z_{ab} \cdot Z_{bc}}{Z_{ab} + Z_{bc} + Z_{ca}} \] \[ Z_c = \frac{Z_{bc} \cdot Z_{ca}}{Z_{ab} + Z_{bc} + Z_{ca}}

Результат: Мы получаем цепь, которая представляет собой последовательное соединение сопротивлений линии \( Z_л \) и сопротивлений новой, преобразованной звезды. Общее сопротивление фазы теперь найти легко:

Z_A = Z_л + Z_a \] \[ Z_B = Z_л + Z_b \] \[ Z_C = Z_л + Z_c

Преобразование «Звезда» в «Треугольник»

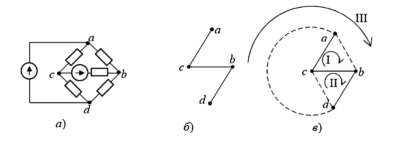
В сложных промышленных сетях часто встречаются смешанные соединения. Если в цепи есть несколько параллельных приемников с разной топологией (и звезда, и треугольник), целесообразно привести их к единому виду. Часто выгоднее преобразовать звезду в эквивалентный треугольник (см. Рис. 3).
На схеме показана исходная звезда \( Z_A \), \( Z_B \), \( Z_C \), преобразуемая в треугольник \( Z»_{AB} \), \( Z»_{BC} \), \( Z»_{CA} \). Этот новый треугольник оказывается включен параллельно с уже существующим треугольником нагрузки \( Z’_{AB} \), \( Z’_{BC} \), \( Z’_{CA} \).

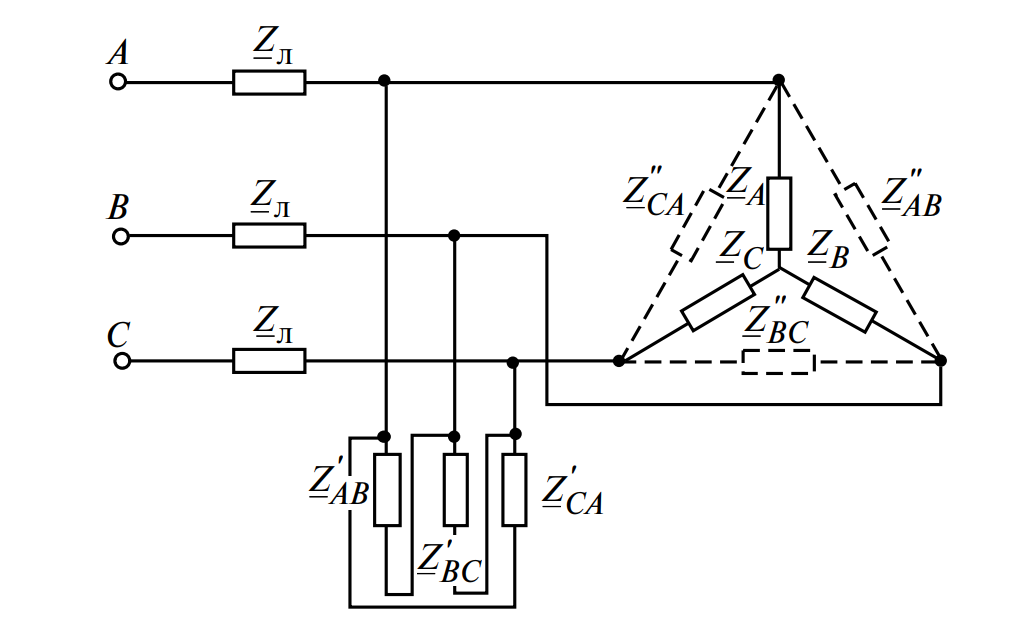
Рис. 3. Трехфазная цепь с несколькими разнородными приемниками

Сопротивления сторон эквивалентного треугольника \( Z» \) рассчитываются по формулам:

Z_{AB}» = Z_A + Z_B + \frac{Z_A \cdot Z_B}{Z_C} \] \[ Z_{BC}» = Z_B + Z_C + \frac{Z_B \cdot Z_C}{Z_A} \] \[ Z_{CA}» = Z_C + Z_A + \frac{Z_C \cdot Z_A}{Z_B}

После такой замены мы получаем два треугольника (исходный со штрихом и преобразованный с двумя штрихами), элементы которых соединены параллельно между точками A-B, B-C и C-A. Результирующее сопротивление эквивалентного треугольника находится по классической формуле параллельного соединения:

Z_{AB} = \frac{Z_{AB}’ \cdot Z_{AB}»}{Z_{AB}’ + Z_{AB}»} \] \[ Z_{BC} = \frac{Z_{BC}’ \cdot Z_{BC}»}{Z_{BC}’ + Z_{BC}»} \] \[ Z_{CA} = \frac{Z_{CA}’ \cdot Z_{CA}»}{Z_{CA}’ + Z_{CA}»}

В итоге мы приходим к схеме, аналогичной показанной на Рис. 2б, метод расчета которой уже известен.

Важное примечание: Взаимное преобразование соединений звезды и треугольника абсолютно корректно применять не только для симметричных, но и для несимметричных приемников. Однако после преобразования вы получите несимметричную эквивалентную схему, расчет которой потребует использования общих методов (например, метода узловых потенциалов).

3. Составление эквивалентных схем на одну фазу

Инженерная практика стремится к оптимизации. При расчете трехфазных цепей со строго симметричными приемниками нет нужды просчитывать все три фазы. Удобно составить расчетную схему только для одной фазы, например, фазы А.

Рассмотрим схему на Рис. 2б. При симметричной нагрузке потенциал общей точки приемников \( n \) (в звезде) становится равным потенциалу нейтральной точки источника \( N \). Это ключевой момент.

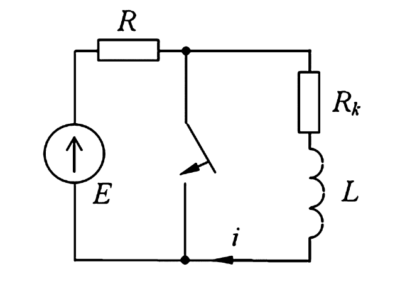
Показана одна линия с источником фазной ЭДС \( E_A \), сопротивлением линии \( Z_л \) и сопротивлением фазы нагрузки \( Z_a \). Точки \( N \) и \( n \) соединены виртуальным проводом.

Рис. 4. Эквивалентная расчетная схема для фазы А

Согласно законам электротехники, если две точки цепи имеют одинаковый потенциал, их можно мысленно (виртуально) соединить коротким замыканием без изменения режима работы схемы. Полученная цепь (Рис. 4) содержит виртуальный нулевой провод, что развязывает фазы друг от друга.

Ток в фазе А определяется по закону Ома:

I_A = \frac{E_A}{Z_л + Z_a}

Остальные токи в трехфазной системе находятся путем простого фазового сдвига полученного значения, так как модули токов равны:

Для фазы B: сдвиг на \(-120^\circ\) (или \(+240^\circ\)).
Для фазы C: сдвиг на \(+120^\circ\).

То есть: \( \dot{I}_B = \dot{I}_A \cdot e^{-j120^\circ} \); \( \dot{I}_C = \dot{I}_A \cdot e^{j120^\circ} \).

Важно помнить, что напряжение на входе такой однофазной схемы — это фазное напряжение \( U_ф \), а протекающий ток — это линейный ток \( I_л \).

Данный метод широко применяется при моделировании работы асинхронных двигателей, силовых трансформаторов и реакторов.

4. Сравнительная таблица соединений

Характеристика	Соединение «Звезда» (Y)	Соединение «Треугольник» (Δ)
Наличие нейтрали	Есть (реальная или виртуальная точка n)	Отсутствует
Связь токов	Линейный ток равен фазному (\( I_л = I_ф \))	Линейный ток в \(\sqrt{3}\) раз больше фазного (при симметрии)
Связь напряжений	Линейное напряжение в \(\sqrt{3}\) раз больше фазного	Линейное напряжение равно фазному (\( U_л = U_ф \))
Применение преобразования	Удобна для учета сопротивлений линий электропередач	Удобна для параллельного включения нагрузок
Преимущество схемы	Возможность получения двух напряжений (фазного и линейного)	Надежность: при обрыве одной фазы двигатель может продолжить вращение (с перегрузкой)

5. Преимущества и недостатки метода преобразования

Преимущества:

Резкое упрощение топологии цепи: уменьшается количество узлов.
Возможность сведения задачи к простой цепи смешанного соединения.
Универсальность: работает как для резисторов, так и для комплексных сопротивлений (импедансов).

Недостатки:

Исчезновение физической нейтральной точки при переходе к треугольнику.
Усложнение формул при несимметричной нагрузке (риск арифметических ошибок).
Потеря наглядности физических процессов в конкретных ветвях после их математического преобразования.

6. Интересныех факты о трехфазных цепях

ЭФФЕКТИВНОСТЬ И СТАНДАРТ: Трехфазная система была выбрана стандартом не случайно. Это минимальное число фаз, позволяющее создать вращающееся магнитное поле без дополнительных устройств и обеспечить постоянную мгновенную мощность генератора.
ПУСК ДВИГАТЕЛЕЙ: Преобразование «звезда-треугольник» часто используется аппаратно при пуске мощных электродвигателей для снижения пусковых токов в 3 раза.
СХЕМА «ЗИГЗАГ»: Существует не только звезда и треугольник, но и соединение «Зигзаг», применяемое в специальных трансформаторах для устранения перекоса фаз.
МНЕМОНИКА ДЛЯ ЗАПОМИНАНИЯ: Формулы преобразования звезды в треугольник мнемонически напоминают «сумму произведений пар, деленную на противолежащее».
ОПАСНОСТЬ ОБРЫВА НУЛЯ: При обрыве нулевого провода в «Звезде» при несимметричной нагрузке происходит «перекос фаз»: на одних приборах напряжение падает, на других — резко возрастает, что ведет к их сгоранию.
ЭКОНОМИЯ НА ЛЭП: Высоковольтные линии передач почти всегда работают без нейтрального провода (треугольник или звезда с заземленной нейтралью только на подстанциях) для экономии металла.
МЕЖДУНАРОДНАЯ МАРКИРОВКА: Символ звезды (Y) и треугольника (Δ) является международным стандартом маркировки клеммных коробок двигателей.

7. FAQ: Часто задаваемые вопросы

1. Можно ли применять эти формулы для цепей постоянного тока?

Да, формулы абсолютно универсальны. Для постоянного тока вместо импедансов \( Z \) используются активные сопротивления \( R \). Метод часто применяется для расчета мостовых схем.

2. Что будет, если перепутать формулы преобразования?

Расчет будет неверным. Сопротивление преобразованной звезды всегда меньше сопротивлений исходного треугольника (делим на сумму), а сопротивление треугольника всегда больше исходной звезды.

3. Влияет ли частота тока на формулы преобразования?

На саму структуру формул частота не влияет, но она влияет на значение индуктивных (\( X_L = \omega L \)) и емкостных (\( X_C = 1/\omega C \)) сопротивлений, входящих в \( Z \).

4. Почему в высоковольтных сетях предпочитают треугольник?

Это не совсем так. В сетях 110 кВ и выше часто используют звезду с глухозаземленной нейтралью для снижения требований к изоляции. Треугольник чаще встречается в распределительных сетях 6-35 кВ и во вторичных обмотках трансформаторов.

5. Можно ли использовать метод для расчета мощности?

Да, но с осторожностью. После преобразования схемы меняются токи в ветвях и падения напряжения на них. Мощность всей цепи сохранится (баланс мощностей), но распределение мощностей по элементам в эквивалентной схеме будет отличаться от реальной.

Заключение

Взаимное преобразование топологий «Звезда» и «Треугольник» является незаменимым инструментом в арсенале инженера-электрика и студента технического ВУЗа. Оно позволяет свести громоздкие сетевые задачи к набору простых последовательно-параллельных вычислений.

Понимание принципов эквивалентирования источников и приемников, а также умение грамотно переходить к однофазным расчетным схемам, закладывает базу для проектирования надежных систем электроснабжения, от бытовой проводки до магистральных линий электропередач.

Нормативная база

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». (Определяет базовые понятия фазы, линии, звезды и треугольника).
ГОСТ 2.702-2011 «Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем».
ГОСТ 29322-2014 «Напряжения стандартные».
ГОСТ 2.755-87 «ЕСКД. Обозначения условные графические в электрических схемах. Устройства коммутационные и контактные соединения».

Список рекомендуемой литературы

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2016.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — Л.: Энергоиздат, 1981.
Зевеке Г.В., Ионкин П.А. Основы теории цепей. — М.: Энергия, 1975.