Синусоидальный ток: определения, параметры, значения

Содержание страницы

1. Синусоидальная функция времени: базовые параметры
2. Действующее (среднеквадратичное) значение
3. Среднее значение и коэффициенты формы
4. Сравнительный анализ форм сигналов
5. Особенности реактивных элементов в цепях синусоидального тока
6. Преимущества и недостатки использования синусоидального тока
7. Интересные факты о синусоидальном токе
8. Часто задаваемые вопросы (FAQ)
Заключение

В современной электроэнергетике и электротехнике доминирующее положение занимают цепи переменного тока. В линейных электрических цепях источники, генерирующие синусоидальную электродвижущую силу (ЭДС), создают в ветвях стационарные синусоидальные токи и напряжения. Понимание базовых определений и математического аппарата, описывающего эти процессы, является фундаментом для расчета сложных инженерных систем, от бытовых сетей до промышленных установок.

Термин «линейная цепь» подразумевает, что параметры ее элементов (активное сопротивление $R$, индуктивность $L$, емкость $C$) не зависят от значений протекающих токов или приложенных напряжений. Именно в таких цепях форма сигнала (синусоида) остается неизменной при прохождении через элементы, изменяются лишь амплитуда и фаза. Наличие нелинейных элементов приводит к искажению формы синусоиды и появлению высших гармоник.

1. Синусоидальная функция времени: базовые параметры

Переменный ток (AC — Alternating Current) — это ток, который изменяется во времени как по величине, так и по направлению. Наиболее распространенной формой переменного тока является синусоидальная. Это обусловлено тем, что синусоидальная функция является единственной периодической функцией, которая не изменяет своей формы при операциях дифференцирования и интегрирования, характерных для цепей с реактивными элементами (индуктивностями и емкостями).

Мгновенное значение синусоидального тока $i(t)$ описывается выражением:

$$i(t) = I_m \sin(\omega t + \phi_0)$$

где:

$I_m$ (Амплитуда) — максимальное значение функции. Для тока измеряется в Амперах (А), для напряжения — в Вольтах (В).
$\omega$ (Угловая частота) — скорость изменения фазы колебаний, выраженная в радианах в секунду (рад/с). Связана с частотой $f$ соотношением $\omega = 2\pi f$.
$\omega t + \phi_0$ (Фаза колебания) — аргумент синуса в текущий момент времени $t$, определяющий состояние колебательного процесса.
$\phi_0$ (Начальная фаза) — значение фазы в момент времени $t=0$. Начальная фаза зависит от выбора начала отсчета времени.

Изображение графика синусоидального тока i(t) с обозначением амплитуды Im, периода T и начальной фазы ϕ

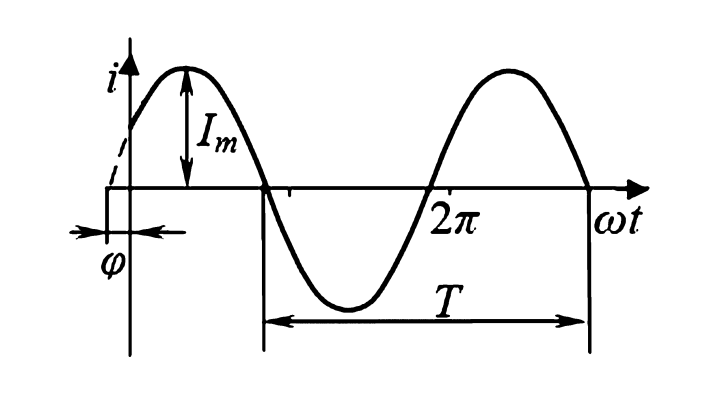
Рисунок 1. График синусоидальной функции времени и ее основные характеристики

Важнейшими временными характеристиками являются:

Период $T$ — наименьший интервал времени (в секундах, с), через который мгновенные значения функции повторяются: $i(t) = i(t+T)$.
Частота $f$ — число полных периодов колебаний в единицу времени. Измеряется в Герцах (Гц), где 1 Гц = 1 с^-1. Связана с периодом как $f = \frac{1}{T}$.

Согласно межгосударственному стандарту ГОСТ 29322-2014 (IEC 60038:2009), в электрических сетях стран СНГ и большей части Европы принята стандартная частота промышленного тока 50 Гц. В США, Канаде и ряде других стран стандартная частота составляет 60 Гц.

2. Действующее (среднеквадратичное) значение

Мгновенные значения тока неудобны для практических расчетов и оценки энергетической эффективности, так как они непрерывно изменяются. Для энергетической характеристики переменного тока используется понятие действующего (эффективного) значения.

Действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное одному периоду $T$, выделяет в том же активном сопротивлении $R$ такое же количество теплоты, что и данный переменный ток.

Количество теплоты $Q_{AC}$, выделяемое переменным током за период:

$$Q_{AC} = \int_{0}^{T} i^2(t) R dt = R \int_{0}^{T} I_m^2 \sin^2(\omega t) dt = R I_m^2 \frac{T}{2}$$

Количество теплоты $Q_{DC}$, выделяемое постоянным током $I$ за то же время:

$$Q_{DC} = I^2 R T$$

Приравнивая $Q_{AC} = Q_{DC}$, получаем выражение для действующего значения:

$$I = \sqrt{\frac{1}{T} \int_{0}^{T} i^2 dt} = \frac{I_m}{\sqrt{2}} \approx 0.707 I_m$$

Аналогично определяется действующее значение синусоидальной ЭДС и напряжения:

$$E = \frac{E_m}{\sqrt{2}} \approx 0.707 E_m; \quad U = \frac{U_m}{\sqrt{2}} \approx 0.707 U_m$$

Именно действующие значения показывают большинство электроизмерительных приборов (амперметры, вольтметры), и именно эти значения указываются в паспортных данных электрооборудования, если не оговорено иное.

3. Среднее значение и коэффициенты формы

Среднее значение переменного тока за полный период равно нулю. Поэтому под средним значением ($I_{ср}$) синусоидальной функции понимают ее среднее значение за положительный полупериод:

$$I_{ср} = \frac{1}{T/2} \int_{0}^{T/2} I_m \sin(\omega t) dt = \frac{2 I_m}{\pi} \approx 0.637 I_m$$

Это значение важно при расчетах выпрямительных устройств и в электрохимии.

Коэффициенты формы и амплитуды

Для характеристики формы периодических сигналов, отличных от синусоиды, используются безразмерные коэффициенты:

Коэффициент амплитуды ($k_a$) — отношение максимального значения к действующему: $k_a = \frac{I_m}{I}$.
Коэффициент формы ($k_\phi$) — отношение действующего значения к среднему: $k_\phi = \frac{I}{I_{ср}}$.

Для идеального синусоидального сигнала эти коэффициенты являются константами: $k_a = \sqrt{2} \approx 1.41$; $k_\phi = \frac{\pi}{2\sqrt{2}} \approx 1.11$. Отклонение от этих значений свидетельствует о наличии нелинейных искажений в сети.

4. Сравнительный анализ форм сигналов

В современной силовой электронике часто встречаются несинусоидальные токи. Сравнение их параметров приведено в таблице ниже.

Таблица 1. Параметры различных форм периодических сигналов
Форма сигнала	Действующее значение ($I$)	Среднее значение ($I_{ср}$)	Коэф. амплитуды ($k_a$)	Коэф. формы ($k_\phi$)
Синусоида	$I_m / \sqrt{2} \approx 0.707 I_m$	$2 I_m / \pi \approx 0.637 I_m$	1.414	1.11
Прямоугольный (меандр)	$I_m$	$I_m$	1.00	1.00
Треугольный (пилообразный)	$I_m / \sqrt{3} \approx 0.577 I_m$	$I_m / 2 = 0.500 I_m$	1.732	1.155

5. Особенности реактивных элементов в цепях синусоидального тока

В отличие от цепей постоянного тока, где установившийся режим определяется только активными сопротивлениями, в цепях переменного тока ключевую роль играют реактивные элементы, создающие сдвиг фаз между током и напряжением.

Индуктивность ($L$). При изменении тока ($di/dt \neq 0$) в катушке возникает ЭДС самоиндукции $e_L = -L \frac{di}{dt}$, которая препятствует изменению тока. В результате ток в идеальной индуктивности отстает от напряжения по фазе на $\pi/2$ (90°).
Емкость ($C$). Ток через конденсатор пропорционален скорости изменения напряжения на его обкладках: $i_C = C \frac{du_C}{dt}$. В идеальном конденсаторе ток опережает напряжение по фазе на $\pi/2$ (90°).

6. Преимущества и недостатки использования синусоидального тока

Преимущества:

Трансформация напряжения: Переменный ток легко трансформировать с помощью электромагнитных трансформаторов, что позволяет эффективно передавать энергию на большие расстояния при высоком напряжении и малых токах, минимизируя потери.
Генерация: Конструкция генераторов переменного тока (синхронных машин) проще, надежнее и дешевле, чем генераторов постоянного тока (отсутствует сложный коллекторно-щеточный узел).
Асинхронные двигатели: Создание вращающегося магнитного поля в трехфазных системах позволяет использовать простые и надежные асинхронные электродвигатели.

Недостатки:

Реактивная мощность: Наличие индуктивных и емкостных элементов приводит к циркуляции реактивной энергии, которая не совершает полезной работы, но загружает линии передачи.
Поверхностный эффект (скин-эффект): Переменный ток вытесняется к поверхности проводника, что уменьшает его эффективное сечение и увеличивает активное сопротивление.
Потери на излучение: Любая цепь переменного тока является источником электромагнитных волн, что может создавать помехи и приводит к дополнительным потерям энергии (особенно на высоких частотах).

7. Интересные факты о синусоидальном токе

Война токов: В конце XIX века шла ожесточенная конкуренция между Томасом Эдисоном (DC) и Николой Теслой с Джорджем Вестингаузом (AC). Победа переменного тока была обеспечена возможностью его эффективной передачи на дальние расстояния.
Почему 50 и 60 Гц? Частота 60 Гц была выбрана Вестингаузом как оптимальная для дуговых ламп того времени. В Европе немецкая компания AEG выбрала 50 Гц, так как это число лучше вписывалось в метрическую систему мер (100 полупериодов в секунду).
400 Гц в авиации: На борту самолетов и морских судов часто используют частоту 400 Гц. Это позволяет значительно уменьшить габариты и вес трансформаторов и двигателей, хотя и увеличивает потери в длинных линиях (которые на борту отсутствуют).
16.7 Гц для железных дорог: В некоторых странах (Германия, Австрия, Швейцария) в тяговых сетях железных дорог исторически используется пониженная частота 16.7 Гц (ранее 16 2/3 Гц) для улучшения коммутации коллекторных тяговых двигателей.
Смертельная опасность: Частота 50-60 Гц является одной из наиболее опасных для человека, так как может вызвать фибрилляцию желудочков сердца даже при относительно малых значениях тока (около 100 мА).
Идеальная синусоида — миф: В реальных электросетях форма напряжения всегда имеет незначительные искажения (гармоники) из-за нелинейных нагрузок (компьютеры, LED-лампы, частотные преобразователи). ГОСТ 32144-2013 нормирует эти искажения.
Звук сети: Характерный низкочастотный гул трансформаторов («гудение сети») вызван магнитострикцией — изменением геометрических размеров сердечника под действием переменного магнитного поля с удвоенной частотой сети (100 Гц для сети 50 Гц).

8. Часто задаваемые вопросы (FAQ)

В чем разница между приборами True RMS и обычными мультиметрами?

Обычные недорогие мультиметры измеряют среднее выпрямленное значение и просто умножают его на коэффициент формы синусоиды (1.11). Они показывают правильное действующее значение только для чистой синусоиды. Приборы класса True RMS измеряют истинное среднеквадратичное значение по сложной формуле и дают корректные показания даже при искаженной форме сигнала (например, на выходе диммера или ИБП).

Что такое мгновенная мощность в цепи синусоидального тока?

Это произведение мгновенных значений напряжения и тока: $p(t) = u(t) \cdot i(t)$. Она пульсирует с удвоенной частотой $2\omega$ относительно среднего значения, которое является активной мощностью.

Может ли действующее значение быть отрицательным?

Нет, действующее значение по определению является корнем из среднего квадрата, поэтому оно всегда положительно. Это энергетическая характеристика.

Почему в США 110-120 В, а в Европе 220-230 В?

Это исторически сложилось из первых ламп Эдисона, рассчитанных на 110 В постоянного тока. При переходе на AC в США сохранили этот уровень напряжения для безопасности. В Европе позже перешли на 220 В для снижения токов и экономии меди в проводах.

Что такое фазовый сдвиг $\phi$?

Это разность начальных фаз напряжения и тока: $\phi = \psi_u — \psi_i$. Он показывает, насколько ток отстает от напряжения или опережает его во времени, и определяет коэффициент мощности ($\cos\phi$).

Как связаны угловая частота $\omega$ и частота вращения генератора?

Для синхронного генератора частота тока $f = \frac{p \cdot n}{60}$, где $p$ — число пар полюсов, а $n$ — обороты в минуту. Угловая частота $\omega = 2\pi f$ жестко привязана к скорости вращения турбины электростанции.

Зависит ли сопротивление резистора от частоты?

В идеальной модели — нет. В реальности, при очень высоких частотах, активное сопротивление проволочных резисторов растет из-за скин-эффекта, а также проявляются их паразитные индуктивности и емкости.

Заключение

Понимание базовых определений синусоидального тока — амплитуды, частоты, фазы и действующих значений — является критически важным для любой работы в области электротехники. Эти параметры не просто математические абстракции; они напрямую связаны с физическими процессами тепловыделения, генерации и передачи энергии. В современных условиях, с ростом количества нелинейных нагрузок, особое значение приобретает корректное измерение этих параметров (True RMS) и контроль качества электроэнергии согласно действующим стандартам.

Нормативная база и литература

ГОСТ 29322-2014 (IEC 60038:2009) Напряжения стандартные.
ГОСТ IEC 60050-103-2024 Международный электротехнический словарь. Часть 103. Управление данными.
ГОСТ R 52002-2003 Электротехника. Термины и определения основных понятий.
ГОСТ 32144-2013 Нормы качества электрической энергии в системах электроснабжения общего назначения.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2016.