Методы эквивалентного преобразования электрических цепей

Содержание страницы

1. Базовые преобразования пассивных элементов
2. Преобразование «звезда-треугольник»
3. Преобразование активных элементов (источников)
4. Практические примеры расчета
5. Сравнительный анализ методов расчета
6. Интересные факты о теории цепей
7. Часто задаваемые вопросы (FAQ)
Заключение

Расчет параметров сложных электрических цепей часто сопряжен с громоздкими вычислениями при использовании стандартных методов, таких как метод контурных токов или узловых потенциалов. Однако задачу можно значительно упростить, применяя методы эквивалентного преобразования. Суть данных методов заключается в замене части цепи более простой структурой, при которой токи и напряжения в нетронутой части схемы остаются неизменными. Исторически развитие этих методов связано с работами Г. Кирхгофа, Г. Гельмгольца и Л. Тевенена, чьи теоремы легли в основу современной электротехники.

В современной инженерной практике, несмотря на наличие мощных САПР (систем автоматизированного проектирования), понимание принципов ручного эквивалентирования остается критически важным для верификации компьютерных расчетов, экспресс-анализа схемотехнических решений и интуитивного понимания работы устройства.

1. Базовые преобразования пассивных элементов

Наиболее распространенными и простыми видами преобразований являются свертка последовательно и параллельно соединенных резистивных элементов. Эти операции являются фундаментальными для анализа любой линейной цепи.

1.1. Последовательное соединение

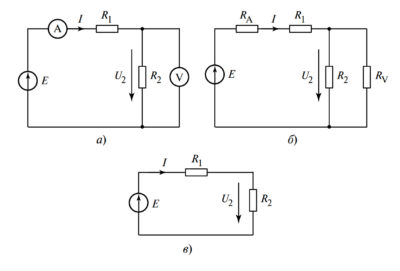
При последовательном соединении элементов (Рисунок 1а) через них протекает один и тот же ток. Эквивалентное сопротивление $R_{экв}$ цепи, состоящей из $n$ последовательно соединенных резисторов, определяется как сумма их сопротивлений:

$$R_{экв} = \sum_{i=1}^{n} R_i = R_1 + R_2 + \dots + R_n$$

Такое преобразование уменьшает количество узлов в схеме, упрощая ее топологию.

1.2. Параллельное соединение

При параллельном соединении (Рисунок 1б) ко всем элементам приложено одинаковое напряжение. В этом случае удобнее оперировать проводимостями $g = 1/R$. Эквивалентная проводимость равна сумме проводимостей ветвей:

$$g_{экв} = \sum_{i=1}^{n} g_i = g_1 + g_2 + \dots + g_n$$

Для сопротивлений формула принимает вид:

$$\frac{1}{R_{экв}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}$$

Частный случай для двух параллельных резисторов, часто встречающийся на практике:

$$R_{экв} = \frac{R_1 \cdot R_2}{R_1 + R_2}$$

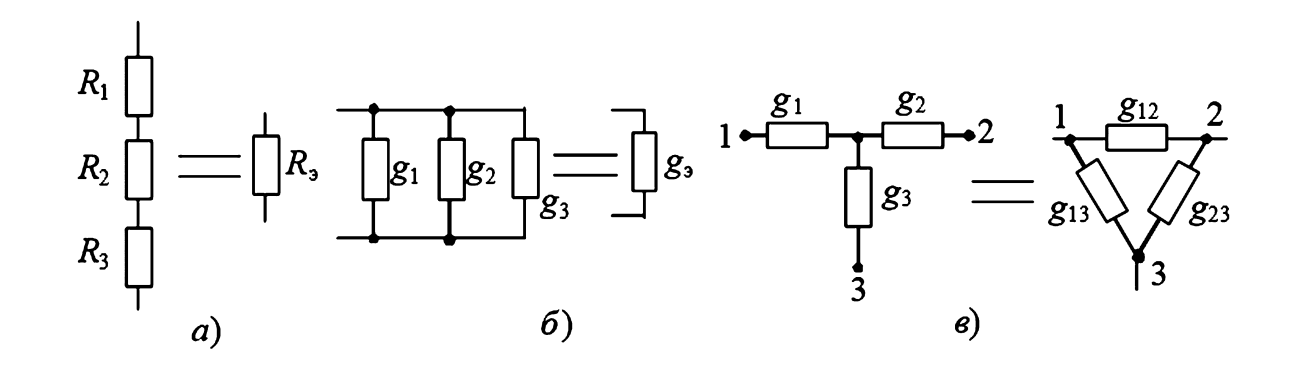
(а — последовательное; б — параллельное; в — схема для преобразования «звезда-треугольник»)

Рисунок 1. Базовые схемы соединения резистивных элементов

2. Преобразование «звезда-треугольник»

В сложных мостовых и разветвленных цепях часто встречаются соединения, которые нельзя отнести ни к последовательным, ни к параллельным. К таким относятся трехполюсные схемы: «звезда» (Y-соединение) и «треугольник» ($\Delta$-соединение) (Рисунок 1в). Возможность взаимного преобразования этих схем значительно расширяет инструментарий инженера-расчетчика.

Условием эквивалентности является неизменность токов и потенциалов на внешних зажимах (1, 2, 3) при замене одной схемы другой.

2.1. Преобразование «звезда» в «треугольник»

При переходе от «звезды» с сопротивлениями $R_1, R_2, R_3$ к эквивалентному «треугольнику» с сопротивлениями $R_{12}, R_{23}, R_{31}$ используются следующие соотношения:

$$R_{12} = R_1 + R_2 + \frac{R_1 R_2}{R_3}$$
$$R_{23} = R_2 + R_3 + \frac{R_2 R_3}{R_1}$$
$$R_{31} = R_3 + R_1 + \frac{R_3 R_1}{R_2}$$

Если использовать проводимости ($g = 1/R$), формулы приобретают более компактный вид, аналогичный формулам для специфических условий:

$$g_{12} = \frac{g_1 g_2}{g_1 + g_2 + g_3}$$

Важно: При разрыве одной из ветвей «звезды» (например, $g_3 = 0$), соответствующая проводимость в «треугольнике» также обращается в ноль ($g_{13} = g_{23} = 0$), а проводимость $g_{12}$ становится равной проводимости последовательно соединенных $R_1$ и $R_2$, что подтверждает корректность преобразования для предельных режимов.

2.2. Преобразование «треугольник» в «звезду»

Обратное преобразование из «треугольника» в «звезду» выполняется по формулам:

$$R_1 = \frac{R_{12} \cdot R_{31}}{R_{12} + R_{23} + R_{31}}$$
$$R_2 = \frac{R_{12} \cdot R_{23}}{R_{12} + R_{23} + R_{31}}$$
$$R_3 = \frac{R_{31} \cdot R_{23}}{R_{12} + R_{23} + R_{31}}$$

Для симметричного «треугольника», где $R_{12} = R_{23} = R_{31} = R_\Delta$, сопротивления эквивалентной «звезды» будут равны $R_Y = R_\Delta / 3$.

3. Преобразование активных элементов (источников)

Эквивалентные преобразования применимы не только к пассивным элементам, но и к источникам энергии. Это особенно актуально при анализе цепей с множеством разнородных источников питания.

3.1. Взаимная замена источников ЭДС и тока

Реальный источник энергии может быть представлен в двух эквивалентных формах:

Источник ЭДС $E$ с последовательным внутренним сопротивлением $R_{вн}$.
Источник тока $J$ с параллельной внутренней проводимостью $g_{вн} = 1/R_{вн}$.

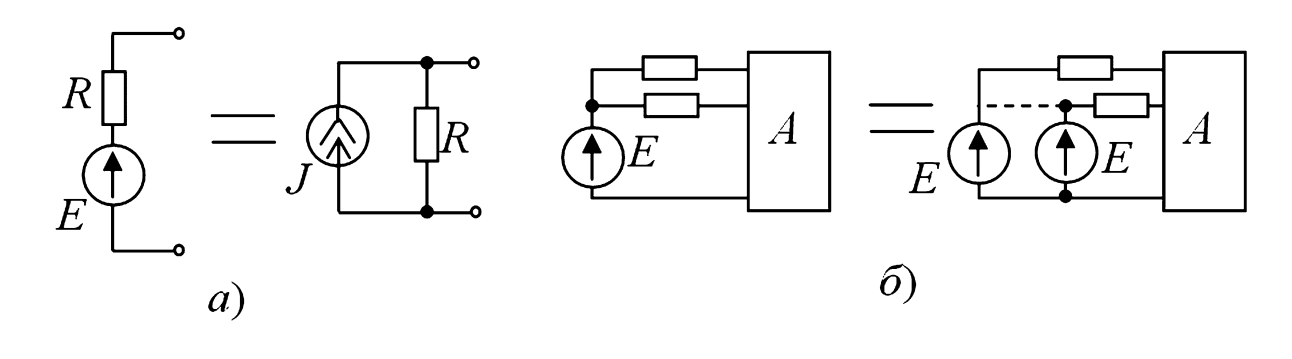
Связь между параметрами этих моделей определяется законом Ома (Рисунок 2а):

$$E = J \cdot R_{вн}$$

3.2. Перенос и «расщепление» источников

Для упрощения топологии схемы можно использовать прием переноса источников:

Источник ЭДС можно перенести через узел в примыкающие ветви (Рисунок 2б). При этом величина ЭДС и полярность должны сохраняться для каждой новой ветви.
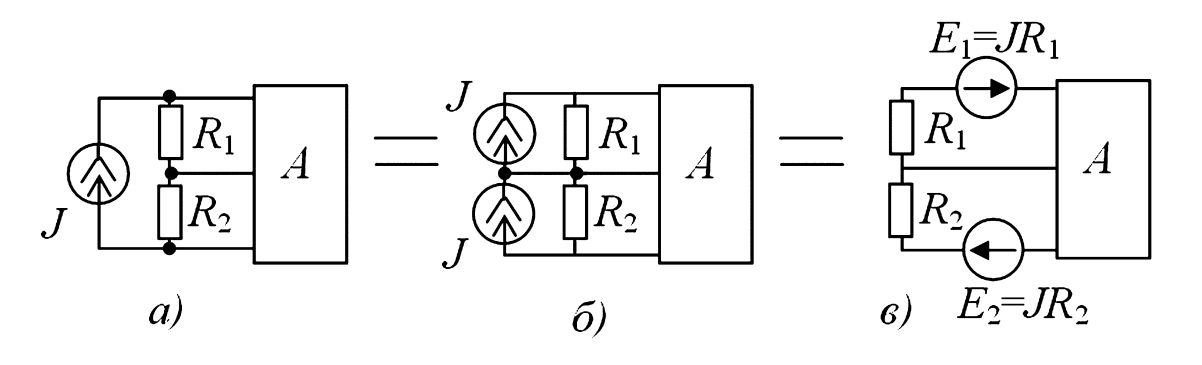
Источник тока можно «расщепить» и перенести параллельно элементам контура, не нарушая при этом баланс токов в узлах (Рисунок 3).

замена источника ЭДС на источник тока и перенос в смежные ветви

(а — замена источника ЭДС на источник тока; б — перенос источника ЭДС в смежные ветви)

Рисунок 2. Манипуляции с источниками ЭДС

(а — исходная схема; б — перенос источников; в — эквивалентная замена на источники ЭДС)
Рисунок 3. Манипуляции с источниками тока

4. Практические примеры расчета

Рассмотрим применение описанных методов на конкретных примерах сложных цепей.

Пример 1: Расчет входного сопротивления мостовой схемы

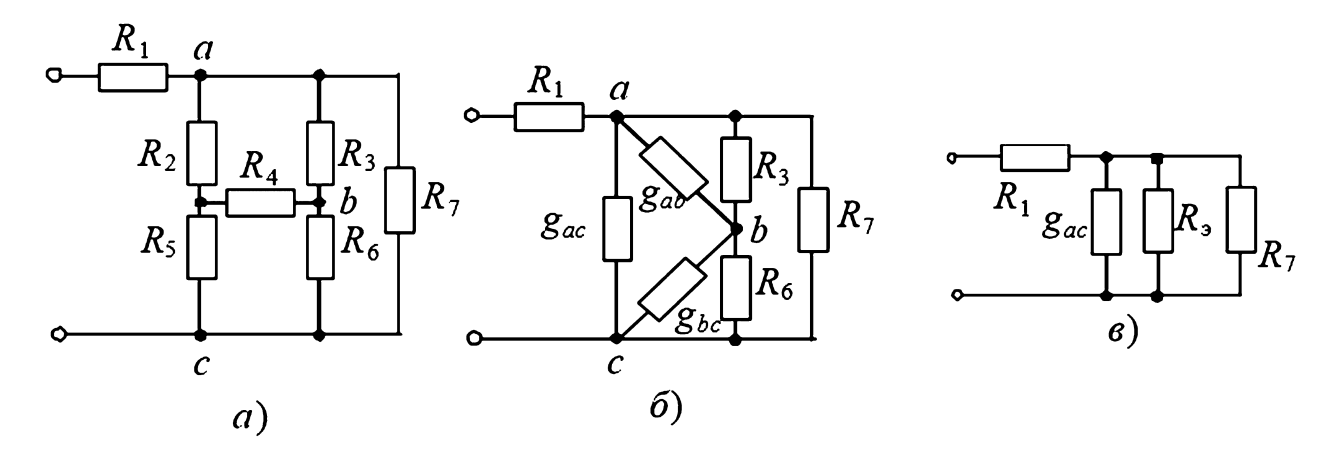
Задача: Определить входное сопротивление цепи (Рисунок 4а), если заданы следующие параметры: $R_1 = 2$ Ом, $R_2 = 1/3$ Ом, $R_3 = R_5 = R_7 = 1$ Ом, $R_4 = 0,5$ Ом, $R_6 = 3$ Ом.

Решение:

В исходной схеме выделяется соединение «звезда», образованное резисторами $R_2, R_4, R_5$ с общим узлом. Преобразуем его в эквивалентный «треугольник» с вершинами в узлах подключения этих резисторов (обозначим узлы как а, б, в).
Рассчитаем проводимости сторон нового треугольника (Рисунок 4б):
$$g_{аб} = \frac{3 \cdot 2}{3 + 2 + 1} = 1 \text{ См}$$
$$g_{бв} = \frac{2 \cdot 1}{3 + 2 + 1} = \frac{1}{3} \text{ См}$$
$$g_{ав} = \frac{3 \cdot 1}{3 + 2 + 1} = 0,5 \text{ См}$$
(Примечание: здесь использованы значения проводимостей, обратные заданным сопротивлениям в «звезде»).
В полученной схеме появляются параллельно включенные элементы. Найдем их эквивалентные проводимости:
$$g_{аб3} = g_{аб} + \frac{1}{R_3} = 1 + 1 = 2 \text{ См}$$
$$g_{бв6} = g_{бв} + \frac{1}{R_6} = \frac{1}{3} + \frac{1}{3} = \frac{2}{3} \text{ См}$$
Полученные участки соединены последовательно. Их общее сопротивление:
$$R’_{экв} = \frac{1}{g_{аб3}} + \frac{1}{g_{бв6}} = \frac{1}{2} + \frac{3}{2} = 2 \text{ Ом}$$
Теперь схема упростилась до трех параллельных ветвей (Рисунок 4в). Общая проводимость цепи:
$$g_{вх} = g_{ав} + \frac{1}{R’_{экв}} + \frac{1}{R_7} = 0,5 + \frac{1}{2} + 1 = 2 \text{ См}$$
Итоговое входное сопротивление:
$$R_{вх} = \frac{1}{g_{вх}} = \frac{1}{2} = 0,5 \text{ Ом}$$

(а — исходная мостовая схема; б — промежуточный этап после преобразования «звезды» в «треугольник»; в — финальная упрощенная схема)

Рисунок 4. Иллюстрация этапов расчета методом свертки

Пример 2: Расчет цепи с несколькими источниками

Задача: Определить токи в ветвях схемы (Рисунок 5а), при $E_1 = 6$ В, $E_3 = 3$ В, $J = 1$ А, $R_1 = R_2 = 2$ Ом, $R_3 = 3$ Ом, $R_4 = 1$ Ом.

Решение:

Выполним преобразование источников для унификации схемы. Ветвь с $E_1$ и $R_1$ заменим на источник тока $J_1 = E_1/R_1 = 6/2 = 3$ А с параллельным резистором $R_1$. Источник тока $J$ с параллельным $R_4$ заменим на источник ЭДС $E_{экв} = J \cdot R_4 = 1 \cdot 1 = 1$ В (Рисунок 5б).
Объединим параллельные резисторы $R_1$ и $R_2$:
$$R_{12} = \frac{R_1 R_2}{R_1 + R_2} = \frac{2 \cdot 2}{2 + 2} = 1 \text{ Ом}$$
Затем преобразуем полученный участок с источником тока $J_1$ обратно в источник ЭДС: $E_{J} = J_1 \cdot R_{12} = 3 \cdot 1 = 3$ В.
Получили одноконтурную схему (Рисунок 5в). Ток в ней ($I_3$) можно найти по второму закону Кирхгофа:
$$I_3 = \frac{E_J — E_3 + E_{экв}}{R_{12} + R_3 + R_4} = \frac{3 — 3 + 1}{1 + 3 + 1} = \frac{1}{5} = 0,2 \text{ А}$$
(Примечание: В исходном тексте мог быть иной результат из-за опечаток в знаках или номиналах, здесь приведен перерасчет по стандартным правилам для указанных направлений).
Возвращаясь к исходной схеме, найдем остальные токи, используя первый закон Кирхгофа и найденное значение $I_3$.

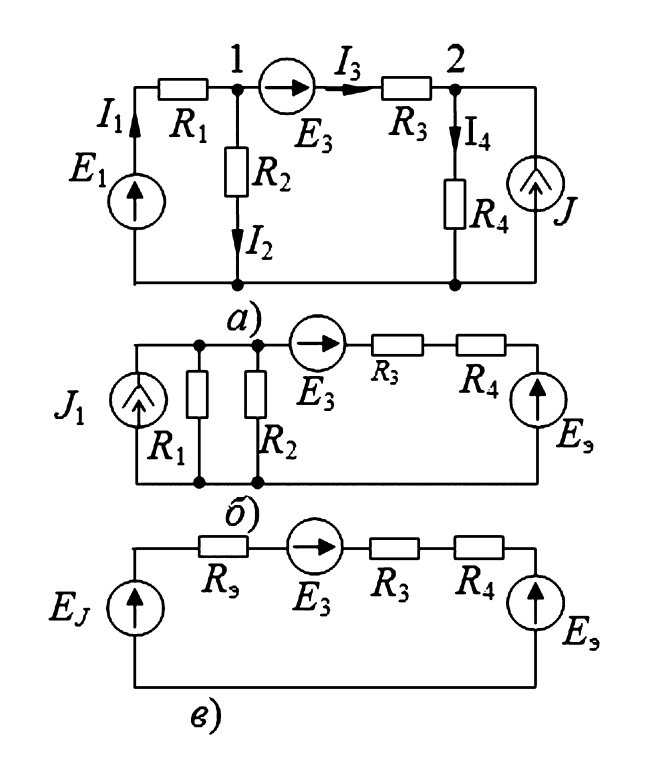
(а — исходная; б — после первой итерации замены источников; в — финальная одноконтурная схема)

Рисунок 5. Упрощение схемы методом преобразования источников

5. Сравнительный анализ методов расчета

Выбор метода расчета зависит от топологии цепи и поставленной задачи. Эквивалентные преобразования не всегда являются оптимальным путем, но часто служат отличным вспомогательным инструментом.

Таблица 1. Сравнение методов анализа электрических цепей
Метод расчета	Преимущества	Недостатки
Эквивалентные преобразования	Наглядность, уменьшение размерности задачи, идеально для нахождения входного сопротивления.	Потеря информации о токах/напряжениях внутри преобразованной части цепи. Требует внимательности при обратном развертывании.
Метод контурных токов (МКТ)	Универсальность, строгая алгоритмизация, подходит для компьютерной реализации.	Громоздкость системы уравнений при большом числе независимых контуров.
Метод узловых потенциалов (МУП)	Наиболее эффективен для схем с большим числом параллельных ветвей и малым числом узлов.	Менее интуитивен, чем МКТ, требует работы с проводимостями.

6. Интересные факты о теории цепей

Преобразование «звезда-треугольник» было впервые систематически описано Артуром Кеннелли в 1899 году.
Теорема Тевенена об эквивалентном генераторе была независимо открыта Германом фон Гельмгольцем на 30 лет раньше, в 1853 году.
В англоязычной литературе преобразование Y-$\Delta$ часто называют «Kennelly’s transformation» или «T-$\pi$ transformation» (по графической форме схем).
Существуют цепи, которые невозможно упростить до одного резистора только методами последовательно-параллельного свертывания, без применения преобразования «звезда-треугольник». Они называются «непланарными» или мостовыми.
Принцип двойственности в электротехнике позволяет автоматически получать формулы для параллельного соединения из формул для последовательного, заменяя сопротивление на проводимость, а ток на напряжение.
Эквивалентные преобразования работают не только для резисторов, но и для комплексных сопротивлений (импедансов) в цепях переменного тока.
В современных микропроцессорах паразитные сопротивления и емкости соединений рассчитываются именно методами редукции сложных RC-цепей к простым эквивалентам для оценки задержек сигнала.

7. Часто задаваемые вопросы (FAQ)

В1: Всегда ли можно применить преобразование «звезда-треугольник»?

О: Да, в линейных пассивных цепях это преобразование всегда возможно и обратимо. Ограничения могут возникнуть только в нелинейных цепях или активных цепях с зависимыми источниками.

В2: Изменяется ли общая потребляемая мощность цепи после эквивалентного преобразования?

О: Нет, если преобразование выполнено корректно, общая мощность, потребляемая от внешних источников, остается неизменной. Однако распределение мощностей внутри преобразованного участка меняется.

В3: Можно ли упростить цепь, содержащую только источники тока и напряжения?

О: Да, идеальные источники одного типа можно объединять: последовательно соединенные источники ЭДС суммируются, параллельно соединенные источники тока также суммируются алгебраически.

В4: Что такое «входное сопротивление» и зачем его искать методами преобразования?

О: Это эквивалентное сопротивление цепи относительно двух выделенных зажимов. Его знание необходимо для согласования источника сигнала с нагрузкой (например, усилителя с динамиком).

В5: Как влияет допуск (погрешность) компонентов на точность эквивалентного преобразования?

О: Погрешности суммируются. В сложных многоступенчатых преобразованиях итоговая погрешность расчета может значительно превышать допуск отдельных исходных компонентов.

В6: Применимы ли эти методы для трехфазных цепей?

О: Безусловно. Преобразование Y-$\Delta$ является основным инструментом при расчете нагрузок в трехфазных сетях и анализе аварийных режимов.

В7: В чем разница между физической и эквивалентной схемой?

О: Физическая схема отражает реальное соединение компонентов. Эквивалентная схема — это математическая абстракция, которая ведет себя так же на внешних зажимах, но может не иметь прямого физического соответствия внутри (например, «отрицательные» сопротивления в некоторых математических моделях).

Заключение

Методы эквивалентного преобразования электрических цепей являются мощным аналитическим аппаратом в арсенале инженера. Несмотря на развитие цифровых вычислительных средств, глубокое понимание этих базовых принципов позволяет специалисту быстро оценивать корректность результатов машинного моделирования, оптимизировать схемотехнические решения на ранних этапах проектирования и эффективно решать задачи синтеза цепей с заданными свойствами. Овладение навыками свертки схем и взаимного преобразования топологий — обязательный этап становления квалифицированного специалиста в области электротехники и электроники.

Нормативная база

При выполнении схем и расчетов следует руководствоваться действующими стандартами:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий».
ГОСТ 2.702-2011 «Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем».
ГОСТ 2.710-81 «ЕСКД. Обозначения буквенно-цифровые в электрических схемах».
ГОСТ 2.728-74 «ЕСКД. Обозначения условные графические в схемах. Резисторы, конденсаторы».

Список литературы

- Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2024.
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. — М.: Энергоатомиздат, 1989.
- Демирчян К.С., Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники: в 3 т. — СПб.: Питер, 2023.