Ферромагнитные материалы: теория, расчет, характеристики

Содержание страницы

1. Фундаментальные основы ферромагнетизма
2. Гистерезис: Магнитная память и потери
3. Материаловедение: Чем заполнить сердечник?
4. Потери в магнитопроводе: Математика тепла
5. Работа в импульсном режиме и подмагничивание
6. Высокочастотные эффекты в обмотках
7. Паразитные параметры и современные технологии
8. Практический пример: Расчет силового импульсного трансформатора
9. Интересные факты о ферромагнетизме и трансформаторах
10. FAQ: Часто задаваемые вопросы
Заключение

Данный материал представляет собой глубокое погружение в мир магнитных материалов и пассивных компонентов, являющихся сердцем любого источника питания, инвертора или преобразователя частоты. Мы пройдем путь от фундаментальной физики доменов и спинов до инженерных расчетов высокочастотных трансформаторов. Вы узнаете, почему сталь греется, как «память» металла (гистерезис) влияет на КПД устройства, и почему на высоких частотах обычный провод перестает работать эффективно. Мы рассмотрим эволюцию от массивного железа 19-го века до современных нанокристаллических сплавов и планарных технологий.

1. Фундаментальные основы ферромагнетизма

1.1. Природа магнитной индукции и напряженности

В основе работы любого индуктивного элемента лежит взаимодействие магнитного поля с веществом. Ключевыми характеристиками здесь выступают вектор магнитной индукции \( B \) и вектор напряженности магнитного поля \( H \). Ферромагнитные материалы — это особый класс веществ (железо, никель, кобальт и их сплавы), которые обладают уникальной способностью многократно усиливать внешнее магнитное поле.

Аналогия: Представьте толпу людей (атомы вещества), каждый из которых держит в руках маленький компас (магнитный момент). В обычном материале (дерево, медь) эти компасы смотрят в хаотичные стороны, и их усилия компенсируют друг друга. В ферромагнетике же существуют целые группы «людей», которые уже договорились смотреть в одну сторону — это называется магнитными доменами. Когда вы прикладываете внешнее поле (команду «Смотреть на Север!»), эти группы охотно и дружно поворачиваются, создавая мощный общий поток.

Связь между индукцией и напряженностью в вакууме линейна, но в ферромагнетиках она носит сложный нелинейный характер. Это описывается фундаментальными уравнениями:

B = \mu_a H $$ $$ B = \mu_0 (H + M)

Где:

\( \mu_a \) — абсолютная магнитная проницаемость среды.
\( \mu_0 = 4\pi \cdot 10^{-7} \) Гн/м — магнитная постоянная (проницаемость вакуума).
\( M \) — намагниченность вещества, показывающая вклад самого материала в итоговое поле.

На практике инженеры чаще оперируют понятием относительной магнитной проницаемости \( \mu_r \), которая показывает, во сколько раз материал «лучше» вакуума проводит магнитный поток:

\mu_a = \mu_0 \mu_r

1.2. Кривая намагничивания и насыщение

Процесс намагничивания не бесконечен. Зависимость индукции \( B \) от напряженности \( H \) называется основной кривой намагничивания (КН). Она представляет собой геометрическое место вершин частных циклов перемагничивания. Для магнитомягких материалов эта кривая практически совпадает с начальной кривой намагничивания, которую получают при первом включении поля для абсолютно размагниченного образца.

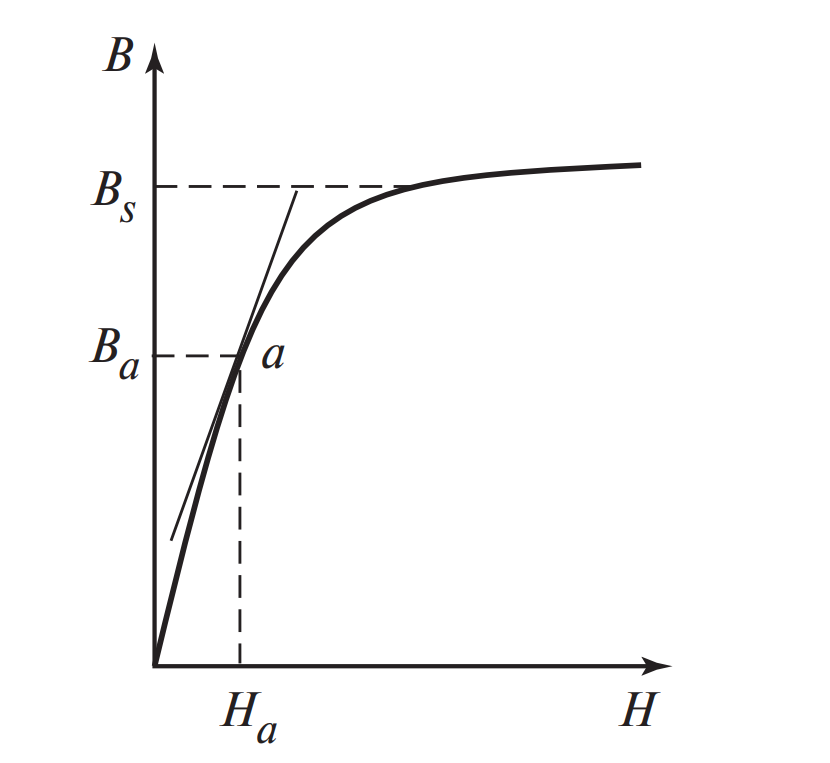
Рис. 1. Основная кривая намагничивания ферромагнетика. Точка \( B_a, H_a \) показывает рабочую точку на линейном участке, \( B_s \) — область насыщения.

Рассмотрим Рисунок 1. При увеличении напряженности \( H \) индукция сначала растет круто (область легкого смещения доменных границ), затем рост замедляется. Пологий участок кривой соответствует режиму насыщения.

Замечание: Насыщение наступает, когда практически все магнитные домены уже ориентированы по полю. Вектор намагниченности \( M \) достигает своего предела \( M_s \). При дальнейшем увеличении тока в обмотке (росте \( H \)) индукция продолжает расти только за счет «вакуумной» составляющей \( \mu_0 H \), что ничтожно мало. Производная в этой зоне \( dB/dH \approx \mu_0 \). Для силовой электроники вход в насыщение часто означает аварию: индуктивность падает, ток лавинообразно растет, ключи сгорают.

В конкретной рабочей точке \( a \) с координатами \( H_a \) и \( B_a \) (см. Рис. 1) поведение материала при малых сигналах описывается дифференциальной магнитной проницаемостью:

\mu_d = \frac{dB}{dH}

Это значение не является константой и меняется по мере движения вдоль кривой, стремясь к минимуму в зоне насыщения. Также различают статическую проницаемость (для постоянного поля) и динамическую (для переменного), о чем мы поговорим ниже.

2. Гистерезис: Магнитная память и потери

2.1. Статическая петля гистерезиса (СПГ)

Ферромагнетики «помнит» свою историю. Если намагнитить материал до насыщения, а затем начать снижать поле до нуля, индукция не вернется к нулю по той же траектории. Она пойдет «выше», сохраняя остаточную индукцию \( B_r \). Это явление называется гистерезисом (от греч. «отставание»).

Рис. 2. Предельная статическая петля гистерезиса. Показаны ключевые точки: коэрцитивная сила \( H_c \) и остаточная индукция \( B_r \).

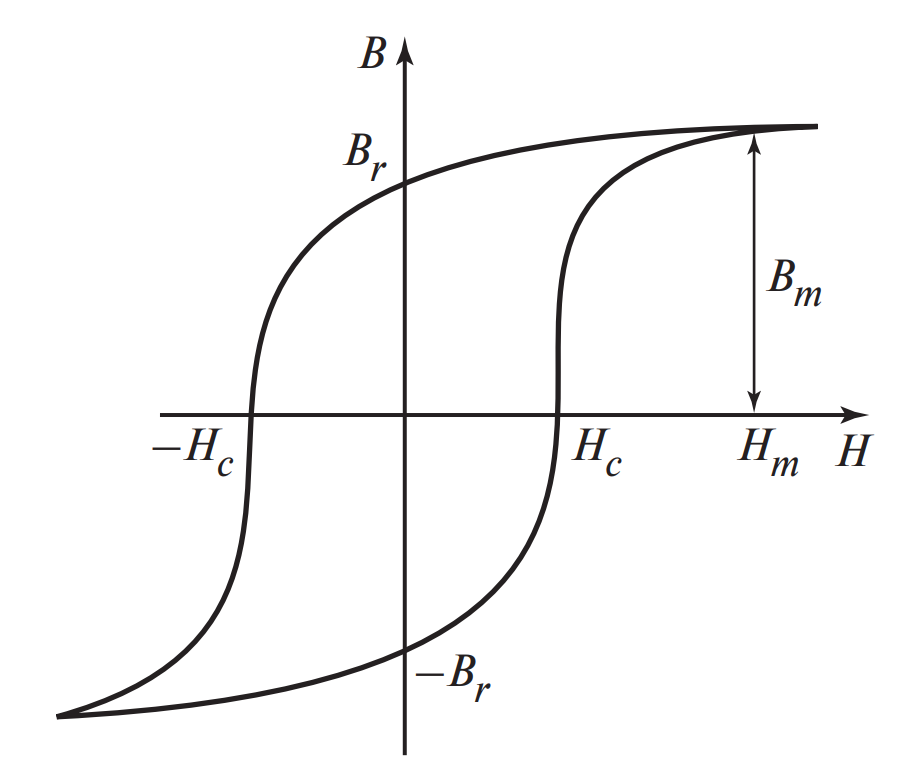
На Рисунке 2 изображена предельная статическая петля гистерезиса (СПГ). Она получается при очень медленном изменении поля (\( dH/dt \approx 0 \)).
Основные параметры петли:

Индукция насыщения (\( B_s \)): Максимально достижимое значение индукции.
Остаточная индукция (\( B_r \)): Значение индукции при выключенном внешнем поле (\( H=0 \)). Именно благодаря \( B_r \) существуют постоянные магниты.
Коэрцитивная сила (\( H_c \)): Напряженность поля обратного знака, которую нужно приложить, чтобы полностью размагнитить материал (довести \( B \) до нуля).

Участки от \( B_m \) до \( -H_c \) соответствуют размагничиванию, а от \( -H_c \) до \( B_m \) — намагничиванию. Чем «квадратнее» петля, тем лучше материал подходит для запоминающих устройств или магнитных усилителей. Это оценивается коэффициентом прямоугольности:

K_{pr} = \frac{B_r}{B_m}

2.2. Динамическая петля гистерезиса (ДПГ)

В реальной силовой электронике процессы протекают быстро. Частоты коммутации достигают сотен килогерц и мегагерц. В этих условиях статическая петля уже не описывает реальность корректно. Используется понятие Динамической петли гистерезиса (ДПГ).

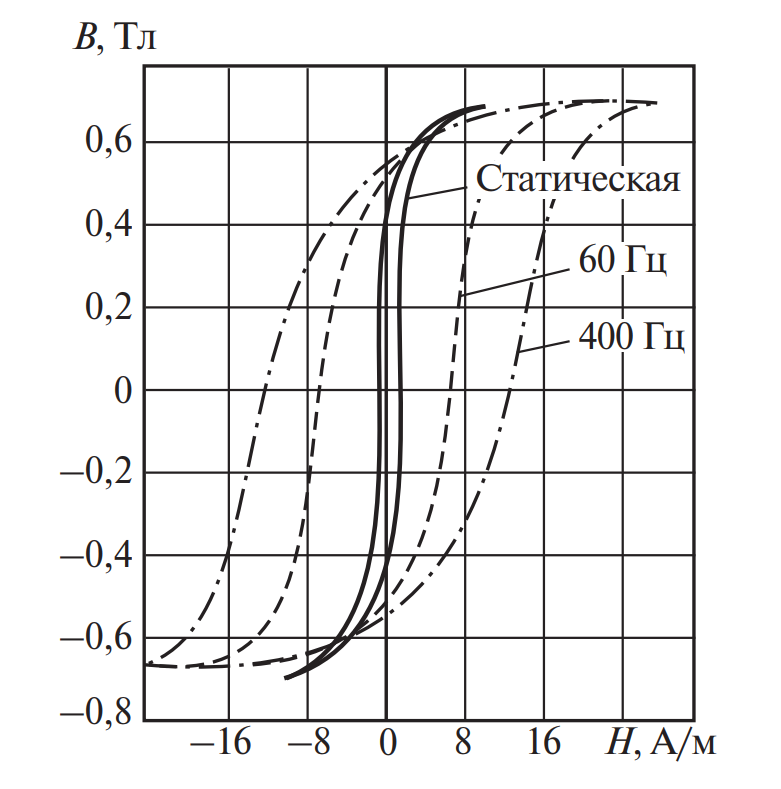
Рис. 3. Трансформация петли гистерезиса с ростом частоты. Внутренняя петля — статическая, внешние — динамические при 400 Гц и выше. Видно уширение петли.

Как видно из Рисунка 3, с ростом частоты петля «раздувается». Это происходит по двум основным причинам:

Магнитная вязкость: Домены имеют инерцию. Они не успевают мгновенно развернуться вслед за быстро меняющимся полем. Это создает эффект запаздывания фазы индукции относительно напряженности.
Вихревые токи (Токи Фуко): Переменное магнитное поле, согласно закону Фарадея, наводит электрические токи в самом теле сердечника. Эти токи создают собственное контрмагнитное поле (правило Ленца), которое препятствует проникновению внешнего поля внутрь материала.

Важно: Площадь внутри петли гистерезиса пропорциональна энергии, теряемой в материале за один цикл перемагничивания. Чем шире петля (ДПГ), тем сильнее греется сердечник. Это основа потерь в стали, которые инженеры стремятся минимизировать.

3. Материаловедение: Чем заполнить сердечник?

Выбор материала зависит от рабочей частоты и требуемой индукции. Современная промышленность предлагает широкий спектр решений.

3.1. Электротехнические стали и Пермаллои (Низкие частоты)

В диапазоне от 50 Гц до 5 кГц королем остается железо.

Кремнистая сталь (Electrical Steel): Добавка кремния (Si) повышает удельное сопротивление железа, снижая вихревые токи. Бывает изотропной (для моторов) и анизотропной (текстурированной, для трансформаторов), где зерна ориентированы вдоль проката.
Пермаллои (Fe-Ni): Сплавы железа с никелем. Обладают феноменально высокой проницаемостью (до 100 000 и выше) и очень узкой петлей гистерезиса (\( H_c < 4 \) А/м). Идеальны для датчиков тока, экранирования и прецизионных трансформаторов.

3.2. Ферриты (Высокие и Сверхвысокие частоты)

Когда частота превышает 10-20 кГц, вихревые токи в металлах становятся катастрофическими. Решением стали ферриты — оксидная керамика.

Ферриты — это не металлы, а полупроводники или даже диэлектрики. Их химическая формула обычно \( MO \cdot Fe_2O_3 \), где \( M \) — двухвалентный металл (Mn, Zn, Ni). Благодаря ионным связям, электроны в них связаны жестко, что обеспечивает огромное электрическое сопротивление (на порядки выше, чем у стали). Вихревые токи в них практически отсутствуют.

MnZn (Марганец-Цинк): Рабочие лошадки силовой электроники. Высокая проницаемость, высокая индукция насыщения (0.3-0.5 Тл). Работают до 1-2 МГц.
NiZn (Никель-Цинк): Имеют очень низкую проницаемость, но огромное сопротивление. Работают на частотах 10 МГц и выше, но чувствительны к температуре и имеют низкий \( B_s \).

3.3. Магнитодиэлектрики и Порошковые материалы

Для дросселей фильтров и реакторов коррекции коэффициента мощности (PFC) нужны материалы, которые тяжело насытить (пологая кривая намагничивания). Раньше для этого пилили физический зазор в феррите. Сейчас используют распределенный зазор.

Альсифер (Sendust): Сплав Al-Si-Fe, размолотый в порошок и склеенный диэлектриком. Каждая частичка металла изолирована, что создает миллионы микрозазоров. Материал имеет низкую проницаемость \( \mu_r \), но линейно работает при огромных токах подмагничивания. Ссылка на стандарты: ГОСТ 19693-74 «Материалы магнитные».

3.4. Аморфные и Нанокристаллические сплавы

Вершина эволюции материалов. Их получают методом быстрой закалки (литье расплава на вращающийся холодный барабан), скорость охлаждения — миллион градусов в секунду. Атомы не успевают построить кристаллическую решетку, застывая в хаосе («металлическое стекло»).

Экстремально низкие потери (в разы меньше ферритов и стали).
Высокая индукция насыщения (1.2 — 1.5 Тл).
Идеальны для миниатюрных, но мощных преобразователей.

Сравнительная таблица магнитных материалов

Материал	Состав	\( B_{sat} \) (Тл)	\( \mu_r \)	Частотный диапазон	Применение
Электротехническая сталь	Fe + Si (3-4%)	1.8 — 2.0	~1 000 — 40 000	50 Гц — 1 кГц	Сетевые трансформаторы, двигатели
Пермаллой	Fe + Ni (~80%)	0.7 — 0.8	50 000 — 100 000+	до 20 кГц	Датчики, экраны, УЗО
Феррит MnZn	Fe, Mn, Zn oxides	0.3 — 0.5	1 000 — 15 000	10 кГц — 2 МГц	Импульсные трансформаторы SMPS
Альсифер (Kool Mµ)	Al, Si, Fe	~1.0	26 — 125	до 500 кГц	Дроссели групповой стабилизации, PFC
Нанокристаллические	Fe, Cu, Nb, Si, B	1.2 — 1.3	20 000 — 80 000	до 100-200 кГц	Компактные трансформаторы, EMI фильтры

4. Потери в магнитопроводе: Математика тепла

Расчет потерь — критический этап проектирования. Перегрев может привести к пробою изоляции или переходу материала через точку Кюри (потеря магнитных свойств).

Классическая эмпирическая формула Штейнмеца (с модификациями) используется повсеместно для оценки удельных объемных потерь \( P_{vol} \) (Вт/см³):

P_{vol} = K \cdot f^{\alpha} \cdot B_m^{\beta}

В тексте стандарта часто встречается нормированная запись, например формула (2.76):

P_{ud} = A_0 \left(\frac{f}{f^*}\right)^{\alpha} \left(\frac{B_m}{B_m^*}\right)^{\beta}

Где \( \alpha \) (обычно 1.2-1.7) и \( \beta \) (обычно 2.0-2.7) — коэффициенты материала. Из формулы видно, что потери растут нелинейно. Удвоение частоты увеличивает потери более чем в два раза, а удвоение индукции — почти в четыре!

При несинусоидальном сигнале (например, ШИМ) спектр напряжения богат высшими гармониками. Потери нужно считать суммированием вклада каждой гармоники:

P_{\Sigma} = \sum_{n=1}^{\infty} P_n(f_n, B_n)

5. Работа в импульсном режиме и подмагничивание

В импульсных источниках питания (однотактных прямоходовых и обратноходовых) трансформатор работает в сложных условиях однополярного намагничивания.

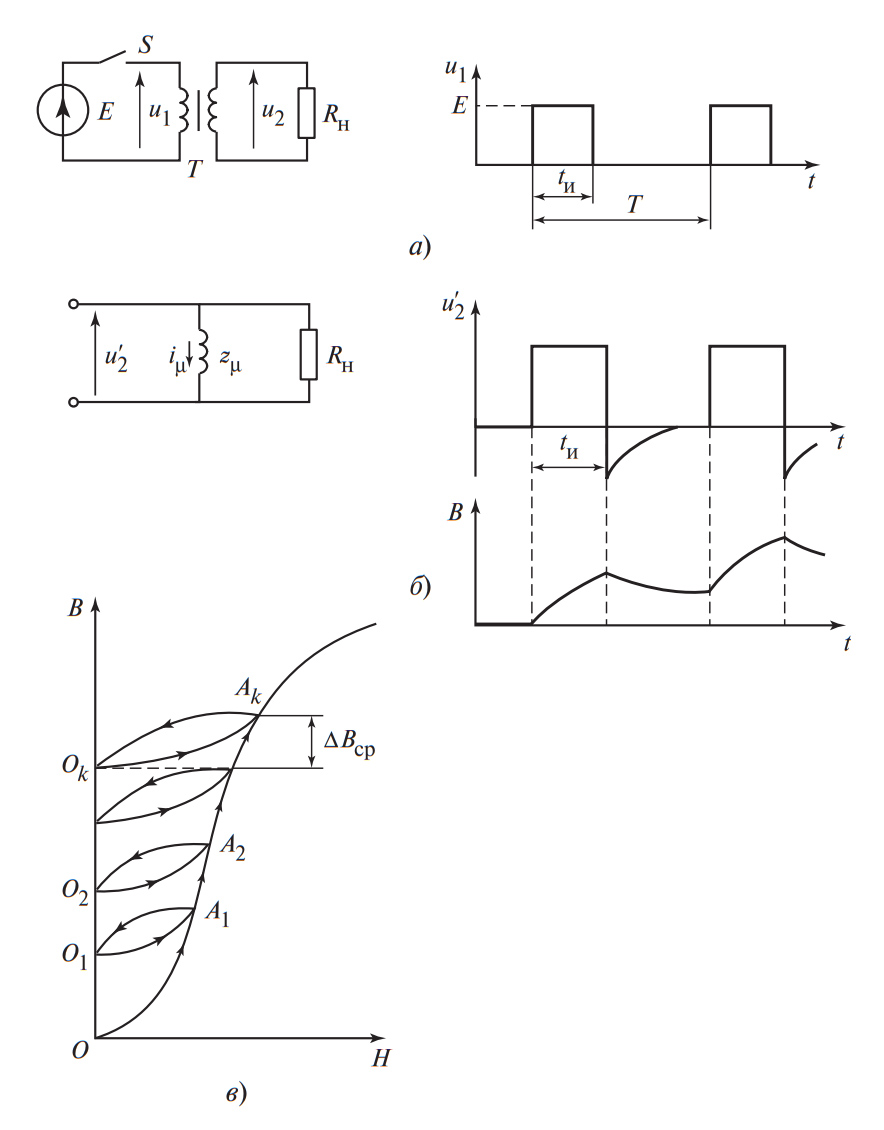
Рис. 4. Процессы в импульсном трансформаторе: а) Схема с ключом S; б) Эквивалентная схема замещения; в) «Блуждание» рабочей точки по петле гистерезиса с выходом на частный цикл.

5.1. Динамика намагничивания (Физика процесса)

Рассмотрим схему на Рис. 4. Когда ключ \( S \) замыкается, к обмотке прикладывается постоянное напряжение \( E \). Согласно закону индукции, поток в сердечнике начинает линейно нарастать. За время импульса \( t_u \) индукция изменится на величину:

\Delta B = \frac{E \cdot t_u}{N_1 \cdot S_m}

Где \( N_1 \) — число витков, \( S_m \) — сечение керна.
На графике (Рис. 4в) рабочая точка движется из \( O \) в \( A_1 \).

5.2. Проблема размагничивания (Reset)

Когда ключ размыкается, магнитный поток должен куда-то деться. Если не обеспечить путь для разрядки энергии (цепь размагничивания или кламп), возникнет огромный выброс напряжения, пробивающий ключ. При наличии цепи сброса, рабочая точка возвращается из \( A_1 \) в \( O_1 \).

Если время паузы недостаточно или цепь размагничивания неэффективна, к началу следующего импульса точка не вернется в ноль. С каждым тактом индукция будет «шагать» вверх (из \( O_1 \) в \( A_2 \), из \( O_2 \) в \( A_3 \)), пока сердечник не влетит в насыщение.

Опасно: Введение немагнитного зазора в магнитопровод помогает «наклонить» петлю гистерезиса (уменьшить остаточную индукцию \( B_r \)), что критически важно для однотактных схем. Это увеличивает диапазон рабочей индукции \( \Delta B \).

6. Высокочастотные эффекты в обмотках

Потери в меди на высоких частотах часто превышают потери в сердечнике. Виной тому два эффекта: скин-эффект и эффект близости.

6.1. Скин-эффект (Поверхностный эффект)

Переменный ток стремится протекать по поверхности проводника, так как в центре вихревые токи компенсируют основной ток. Эффективное сечение провода падает, сопротивление растет. Глубина проникновения тока (скин-слой) \( \delta \) определяется формулой:

\delta = \sqrt{\frac{2\rho}{\omega\mu_0\mu_r}}

Для меди при 100°C:

50 Гц: \( \delta \approx 9 \) мм
50 кГц: \( \delta \approx 0.3 \) мм
1 МГц: \( \delta \approx 0.07 \) мм

Использовать провод толще \( 2\delta \) бессмысленно — середина не работает. Решение — литцендрат (жгут из множества тонких изолированных жил).

6.2. Эффект близости (Proximity effect)

Магнитное поле от соседних витков также наводит вихревые токи. Это явление часто более губительно, чем скин-эффект, особенно в многослойных обмотках.

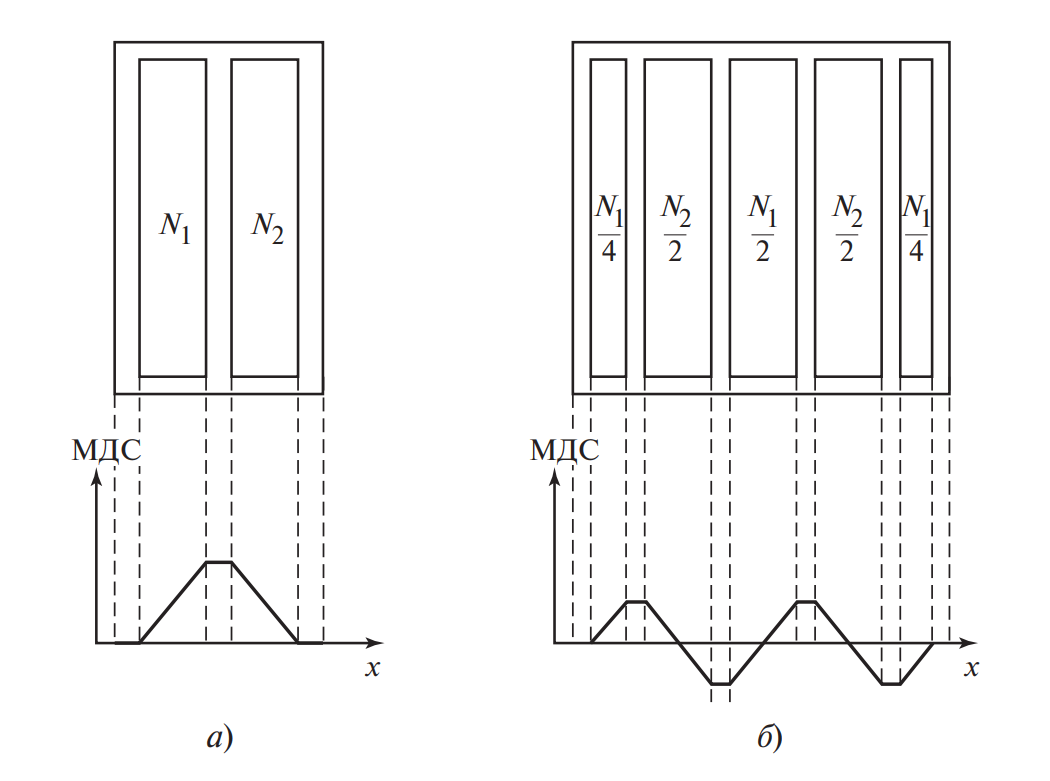
Рис. 5. Распределение МДС в окне намотки. а) Простая намотка: МДС растет треугольником, потери максимальны в слоях у зазора между первичкой и вторичкой. б) Секционирование (сэндвич) разбивает треугольник МДС, снижая пиковую напряженность и потери в разы.

Как показано на Рис. 5, правильное чередование слоев (Первичная-Вторичная-Первичная) радикально снижает потери за счет уменьшения локальной напряженности поля.

7. Паразитные параметры и современные технологии

7.1. Эквивалентная схема с паразитными элементами

На высоких частотах трансформатор — это не просто индуктивность. Это сложная колебательная система (Рис. 6).

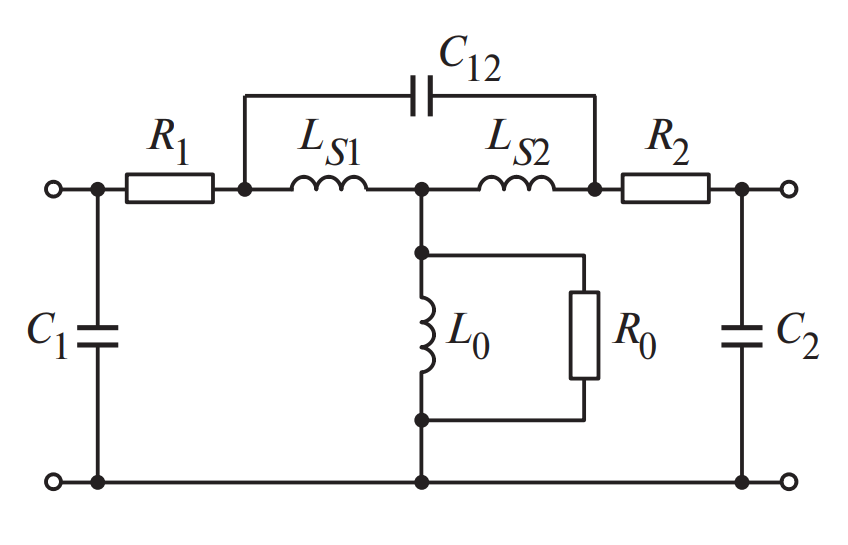
Рис. 6. Полная высокочастотная модель трансформатора: \( L_{S1}, L_{S2} \) — индуктивности рассеяния, \( C_{12} \) — межобмоточная емкость, \( C_1, C_2 \) — собственные емкости обмоток.

Индуктивность рассеяния (\( L_s \)): Энергия поля, которая не сцепилась со вторичной обмоткой. Она вызывает выбросы напряжения при коммутации.
Межвитковая емкость: При резких фронтах напряжения ток течет через изоляцию (ток смещения), минуя индуктивность.

7.2. Планарные трансформаторы

Современный тренд — отказ от намоточных проводов в пользу печатных плат (PCB) или штампованных медных пластин. Планарная технология позволяет «впечатать» обмотки внутрь многослойной платы, а сердечник надеть поверх (конструкции E-Planar).

Преимущества:

Идеальная повторяемость параметров (индуктивности рассеяния).
Низкий профиль (плоские).
Отличный теплоотвод на радиатор.
Высокая механическая прочность.

Это ключевая технология для создания DC/DC преобразователей высокой плотности мощности (сотни ватт на кубический дюйм).

8. Практический пример: Расчет силового импульсного трансформатора

Чтобы закрепить теоретический материал, проведем полный цикл расчета реального трансформатора для импульсного источника питания (ИИП).

8.1. Техническое задание (ТЗ)

Спроектируем трансформатор для классического полумостового преобразователя (Half-Bridge), который часто используется в блоках питания компьютеров и мощных зарядных устройствах.

Входное напряжение: Сеть 230 В (после выпрямителя на конденсаторах полумоста будет делиться пополам: \( U_{in} \approx 155 \) В).
Выходное напряжение (\( U_{out} \)): 24 В.
Выходная мощность (\( P_{out} \)): 500 Вт (Ток нагрузки \( I_{out} \approx 21 \) А).
Рабочая частота (\( f \)): 50 кГц.
Максимальная температура перегрева: +40°C относительно среды.

8.2. Шаг 1: Выбор материала и сердечника

Поскольку частота 50 кГц, электротехническая сталь не подходит из-за огромных потерь на вихревые токи. Выбираем феррит марки N87 (или аналог PC40, 3C90) — это стандартный марганец-цинковый (MnZn) материал для силовой электроники.

Для мощности 500 Вт на частоте 50 кГц необходимо выбрать сердечник с достаточной габаритной мощностью. Используем популярную методику оценки произведения площадей \( A_p \) (произведение площади окна на площадь сечения керна).
Опытным путем для 500 Вт выбираем сердечник типоразмера ETD 44/22/15.

Справочные данные сердечника ETD 44:
Эффективное сечение магнитопровода: \( A_e = 173 \, \text{мм}^2 \).
Площадь окна для намотки: \( A_w = 213 \, \text{мм}^2 \).

8.3. Шаг 2: Расчет витков первичной обмотки

Это самый критический этап. Нам нужно найти баланс: мало витков — сердечник войдет в насыщение (взрыв ключей); много витков — перегрев обмотки и лишние потери меди.
Используем фундаментальный закон электромагнитной индукции Фарадея для прямоугольного импульса:

N_1 = \frac{U_{in(min)} \cdot t_{on}}{\Delta B \cdot A_e}

Где:

\( U_{in(min)} \) — минимальное амплитудное напряжение на первичной обмотке (учитываем просадки сети). Возьмем \( 140 \) В.
\( t_{on} \) — время длительности импульса. При частоте 50 кГц период \( T = 20 \) мкс. В полумосте макс. коэффициент заполнения \( D \approx 0.45 \) (оставляем «мертвое время» для защиты от сквозных токов).
\( t_{on} = 20 \cdot 0.45 = 9 \) мкс.
\( \Delta B \) — размах индукции. Феррит N87 насыщается при \( 0.39 \) Тл (при 100°C). Для надежности и снижения потерь на гистерезис выбираем рабочую амплитуду \( B_{max} = 0.15 \) Тл. Так как схема двухтактная, индукция меняется от \( -0.15 \) до \( +0.15 \), итого размах \( \Delta B = 0.3 \) Тл.

Подставляем значения:

N_1 = \frac{140 \cdot 9 \cdot 10^{-6}}{0.3 \cdot 173 \cdot 10^{-6}} = \frac{1.26 \cdot 10^{-3}}{51.9 \cdot 10^{-6}} \approx 24.27

Округляем до ближайшего целого. Примем \( N_1 = 24 \) витка.
Проверим реальную амплитуду индукции: \( B_{real} = \frac{140 \cdot 9}{24 \cdot 173} \approx 0.303 \) Тл (размах), или \( \pm 0.151 \) Тл амплитуды. Это безопасный режим, далекий от насыщения (0.39 Тл).

8.4. Шаг 3: Расчет вторичной обмотки

Определяем коэффициент трансформации \( n \). Нам нужно получить 24 В на выходе.
Однако нужно учесть падение напряжения на выпрямительных диодах Шоттки (\( V_d \approx 0.6 \) В) и падение на дросселе и проводах (\( V_{loss} \approx 1 \) В).
Требуемое напряжение вторички: \( U_2 = 24 + 0.6 + 1 = 25.6 \) В.

n = \frac{U_{in(nom)}}{U_2} = \frac{155}{25.6} \approx 6.05

Номинальное напряжение на первичке принимаем 155 В.
Число витков вторичной обмотки:

N_2 = \frac{N_1}{n} = \frac{24}{6.05} \approx 3.96

Округляем до 4 витков.

Уточнение: Так как выход 24 В двухполупериодный (со средней точкой), нам нужно мотать 4 + 4 витка.

8.5. Шаг 4: Борьба со скин-эффектом (Выбор провода)

Теперь определим диаметр провода. Вспоминаем про скин-эффект. Глубина проникновения тока \( \Delta \) в медь при 50 кГц:

\Delta_{Cu} = \frac{66.1}{\sqrt{f}} = \frac{66.1}{\sqrt{50000}} \approx 0.296 \, \text{мм}

Это значит, что использовать провод диаметром более \( 2 \cdot \Delta \approx 0.6 \) мм бессмысленно — его центр не будет проводить ток, а будет только греться.
Оптимальный диаметр жилы выбираем 0.5 мм.

8.6. Шаг 5: Расчет сечения обмоток по току

Зададимся плотностью тока \( J \). Для импульсных трансформаторов с естественным охлаждением нормой считается \( J = 4 \dots 5 \) А/мм². Возьмем \( 4 \) А/мм².

Для первичной обмотки:

Мощность 500 Вт. Средний ток потребления: \( I_{in} \approx 500 / 155 \approx 3.2 \) А.
Эффективный ток (RMS) с учетом формы импульса будет выше, примерно 4 А.
Требуемое сечение: \( S_{cu1} = 4 / 4 = 1 \, \text{мм}^2 \).
Сечение одного провода Ø0.5 мм: \( S_{wire} = \pi \cdot 0.25^2 \approx 0.196 \, \text{мм}^2 \).
Количество жил в жгуте (литцендрат): \( 1 / 0.196 \approx 5.1 \). Берем 5 жил по 0.5 мм.

Для вторичной обмотки:

Ток нагрузки 21 А.
Требуемое сечение: \( S_{cu2} = 21 / 4 = 5.25 \, \text{мм}^2 \).
Количество жил в жгуте: \( 5.25 / 0.196 \approx 26.7 \).
Берем 27 жил по 0.5 мм (или готовую «косичку»).

8.7. Шаг 6: Проверка на собираемость (Коэффициент заполнения окна)

Влезет ли вся эта медь в окно сердечника ETD 44?

Площадь меди первички: \( 24 \text{ витка} \cdot 5 \text{ жил} \cdot 0.196 \approx 23.5 \, \text{мм}^2 \).
Площадь меди вторички: \( (4+4) \text{ витка} \cdot 27 \text{ жил} \cdot 0.196 \approx 42.3 \, \text{мм}^2 \).
Итого «чистой» меди: \( 23.5 + 42.3 = 65.8 \, \text{мм}^2 \).

Площадь окна \( A_w = 213 \, \text{мм}^2 \).
Коэффициент заполнения по меди:

K_{fill} = \frac{65.8}{213} \approx 0.31

Вывод: \( K_{fill} = 0.31 \) — это отличный результат. Реально с учетом изоляции проводов (лак), межслойной изоляции (майларовая лента) и неплотности намотки (круглое к круглому) окно будет заполнено примерно на 60-70%. Трансформатор собирается легко.

Результат расчета

Параметр	Значение
Сердечник	Ferrite ETD 44 (Material N87)
Первичная обмотка (230В)	24 витка, жгут 5×0.5 мм
Вторичная обмотка (24В)	4 + 4 витка, жгут 27×0.5 мм
Зазор	0 мм (сердечник смыкается плотно, без прокладки)
Максимальная индукция	0.15 Тл (далеко от насыщения)

9. Интересные факты о ферромагнетизме и трансформаторах

Магнитный «голос». Характерное гудение мощных трансформаторов, которое мы слышим на подстанциях, вызвано явлением магнитострикции. Под действием переменного магнитного поля геометрические размеры кристаллической решетки сердечника меняются (материал то сжимается, то расширяется) с частотой сети, заставляя воздух вибрировать.
Замораживание хаоса. Производство аморфных сплавов (металлических стекол) напоминает сцену из научной фантастики: расплавленный металл выливают на вращающийся барабан, охлаждая его со скоростью миллион градусов в секунду. Атомы просто не успевают выстроиться в решетку, застывая в хаотичном состоянии, что дает материалу уникальные магнитные свойства.
Немецкие корни. Термин «литцендрат» (многожильный провод для борьбы со скин-эффектом) происходит от немецких слов Litzen (пряди) и Draht (проволока). Эта технология, разработанная еще в начале XX века для радио, сегодня является стандартом для сверхбыстрых зарядок электромобилей.
Точка невозврата. У каждого ферромагнетика есть своя температура Кюри. Если нагреть обычный магнит выше этой температуры (для железа это 770°C), тепловое движение атомов разрушит порядок магнитных доменов, и материал мгновенно превратится в парамагнетик, полностью потеряв свои магнитные свойства.
Космическая память. До эры полупроводниковой памяти компьютеры использовали ферритовые сердечники для хранения данных. Петля гистерезиса с высокой прямоугольностью позволяла кольцу «помнить» состояние намагниченности (0 или 1) даже при отключении питания. Такие системы памяти летали на ранних космических кораблях «Аполлон».
Парадокс пустоты. Введение воздушного зазора в сплошной магнитный сердечник, казалось бы, должно ухудшать его свойства. Однако в силовой электронике это осознанная необходимость: «разрыв» магнитной цепи предотвращает насыщение сердечника при протекании постоянного тока, позволяя дросселю накапливать огромную энергию в самом объеме этого зазора.
Плоский мир. Современные планарные трансформаторы могут быть тоньше монеты. Вместо проволоки в них используются дорожки многослойной печатной платы, а сам сердечник часто «прошивает» плату насквозь. Это позволило создать адаптеры питания для ноутбуков, которые помещаются в карман рубашки.

10. FAQ: Часто задаваемые вопросы

Почему трансформатор нагревается даже без нагрузки?

Даже если к вторичной обмотке ничего не подключено, по первичной течет ток намагничивания. Сердечник постоянно перемагничивается (50 раз в секунду или чаще). Энергия тратится на поворот магнитных доменов (потери на гистерезис) и на протекание вихревых токов внутри металла. Это и вызывает нагрев, называемый «потерями в стали».

Что такое насыщение сердечника и почему оно опасно?

Насыщение — это состояние, когда все магнитные домены материала уже выстроились вдоль поля. Материал больше не может усиливать магнитный поток. В этот момент его магнитная проницаемость резко падает до уровня вакуума, а индуктивность обмотки стремится к нулю. Это приводит к лавинообразному росту тока, который может мгновенно сжечь транзисторы преобразователя.

Можно ли использовать обычный железный трансформатор на высокой частоте?

Нет. Обычная электротехническая сталь имеет низкое удельное сопротивление. При повышении частоты (например, до 20 кГц) вихревые токи в ней станут настолько сильными, что сердечник раскалится за секунды, как индукционная плита. Для высоких частот используют ферриты (которые являются диэлектриками) или тончайшие ленты аморфных сплавов.

В чем смысл использования многожильного провода (литцендрата)?

На высоких частотах ток вытесняется на поверхность проводника (скин-эффект), и середина толстого провода «не работает», просто занимая место. Литцендрат состоит из сотен тонких изолированных жил, диаметр каждой из которых меньше глубины проникновения тока. Это заставляет ток течь по всему сечению жгута, снижая сопротивление и нагрев.

Зависит ли КПД трансформатора от его размера?

Да, существует так называемый масштабный эффект. Как правило, чем крупнее трансформатор, тем выше его КПД. Огромные сетевые трансформаторы на электростанциях имеют КПД 99% и выше, тогда как миниатюрные импульсные трансформаторы в зарядных устройствах обычно работают с КПД 95–97%. Однако это также сильно зависит от используемых материалов и частоты преобразования.

Заключение

Электромагнитные компоненты остаются фундаментом силовой электроники. Несмотря на развитие полупроводников (GaN, SiC), именно магнитные элементы определяют габариты, вес и КПД преобразователей. Понимание физики процессов — от доменной структуры до скин-эффекта в обмотках — позволяет инженерам создавать устройства, о которых полвека назад можно было только мечтать: сварочные инверторы размером с книгу и зарядки для ноутбуков размером со спичечный коробок. Будущее за интеграцией магнетиков, повышением частот до десятков мегагерц и применением новых композитных наноматериалов.

Список нормативной базы и литературы

ГОСТ R 52002-2003 «Электротехника. Термины и определения основных понятий».
ГОСТ 19693-74 «Материалы магнитные. Термины и определения».
ГОСТ IEC 60076-1-2011 «Трансформаторы силовые. Часть 1. Общие требования».
ГОСТ 20906-75 «Средства измерений магнитных величин».
Семенов Б.Ю. «Силовая электроника: от простого к сложному».
Мелешин В.И. «Транзисторная преобразовательная техника».
Magnetics Inc. «Ferrite Core Design Guide».