Емкость в цепи синусоидального тока: расчет и графики

Содержание страницы

1. Основные соотношения между током и напряжением
2. Фазовые соотношения
3. Энергетические процессы: Мощность
4. Графическое представление и диаграммы
5. Сравнительный анализ и экспертные данные
6. 7 Интересных фактов о емкости
7. Часто задаваемые вопросы (FAQ)
Заключение

Емкостный элемент (или конденсатор) в цепи переменного тока — это один из фундаментальных компонентов электротехники, обладающий свойством накапливать энергию электрического поля. В отличие от резистора, идеальная емкость не рассеивает энергию в виде тепла, а лишь обменивается ею с источником.

История изучения этого явления восходит к 1745 году, когда была изобретена Лейденская банка, а математическое описание процессов переменного тока позже систематизировали такие ученые, как Майкл Фарадей (в честь которого названа единица емкости) и Джеймс Клерк Максвелл. Понимание работы конденсатора в цепях синусоидального тока критически важно для проектирования фильтров, компенсаторов реактивной мощности и радиотехнических цепей.

1. Основные соотношения между током и напряжением

В теории электрических цепей идеальный емкостный элемент $ C $ рассматривается как компонент, в котором отсутствуют потери энергии (активное сопротивление диэлектрика и обкладок стремится к нулю). Мгновенные значения напряжения $ u $ и тока $ i $ в таком элементе связаны фундаментальной дифференциальной зависимостью:

i = C \frac{du}{dt}

Рассмотрим случай, когда к элементу приложено синусоидальное напряжение. Пусть закон изменения напряжения во времени описывается выражением:

u(t) = U_m \sin(\omega t + \psi_u)

Где:
$ U_m $ — амплитуда напряжения,
$ \omega $ — угловая частота,
$ \psi_u $ — начальная фаза напряжения.

Подставив выражение напряжения в формулу тока и выполнив операцию дифференцирования, мы получаем:

i(t) = C \frac{d}{dt} [U_m \sin(\omega t + \psi_u)] = \omega C U_m \cos(\omega t + \psi_u)

Используя формулы приведения тригонометрических функций (переход от косинуса к синусу), запишем окончательное выражение для мгновенного значения тока:

i(t) = I_m \sin \left( \omega t + \psi_u + \frac{\pi}{2} \right) = I_m \sin(\omega t + \psi_i)

1.1. Амплитуда и емкостное сопротивление

Амплитуда тока $ I_m $ определяется выражением:

I_m = \omega C U_m = B_C U_m = \frac{U_m}{X_C}

В этой формуле введены важные электротехнические параметры:

$ B_C = \omega C $ — емкостная проводимость (измеряется в Сименсах, См).
$ X_C = \frac{1}{B_C} = \frac{1}{\omega C} $ — емкостное сопротивление (измеряется в Омах, Ом).

Важно: Емкостное сопротивление $ X_C $ обратно пропорционально частоте. Для постоянного тока ($ \omega = 0 $) сопротивление конденсатора бесконечно велико (разрыв цепи).

2. Фазовые соотношения

Анализируя полученные уравнения фаз, можно сделать ключевой вывод о работе емкости в цепях переменного тока. Начальная фаза тока равна:

\psi_i = \psi_u + \frac{\pi}{2}

Это означает, что ток в емкостном элементе опережает напряжение по фазе на 90° (или на $ \pi/2 $ радиан). Разность фаз (сдвиг фаз) между напряжением и током составляет:

\phi = \psi_u — \psi_i = -\frac{\pi}{2}

Справедливо и обратное утверждение: напряжение отстает от тока. Мы можем выразить напряжение через ток следующим образом:

u(t) = X_C I_m \sin \left( \omega t + \psi_i — \frac{\pi}{2} \right)

3. Энергетические процессы: Мощность

Мгновенная мощность $ p(t) $ в цепи определяется как произведение мгновенных значений напряжения и тока. Используя тригонометрические преобразования, получим:

p(t) = u(t) \cdot i(t) = U_m \sin(\omega t + \psi_u) \cdot I_m \cos(\omega t + \psi_u)

Используя формулу синуса двойного угла $ 2\sin\alpha\cos\alpha = \sin(2\alpha) $ и переходя к действующим значениям $ U = U_m/\sqrt{2} $ и $ I = I_m/\sqrt{2} $:

p(t) = \frac{U_m I_m}{2} \sin(2(\omega t + \psi_u)) = UI \sin(2(\omega t + \psi_u))

Анализ мощности:

Мгновенная мощность изменяется с удвоенной частотой $ 2\omega $ по сравнению с током и напряжением.
Активная мощность $ P $ (среднее значение мгновенной мощности за период) в идеальном емкостном элементе равна нулю. Это подтверждается тем, что интеграл от синусоиды за период равен нулю.
Энергия электрического поля $ W_э(t) $, запасенная в емкости, также пульсирует с удвоенной частотой: $W_э = \frac{C u^2}{2}$

4. Графическое представление и диаграммы

Для наглядного понимания процессов ниже приведены графики мгновенных значений и векторная диаграмма. Обратите внимание на строгое соответствие нумерации описанию процессов.

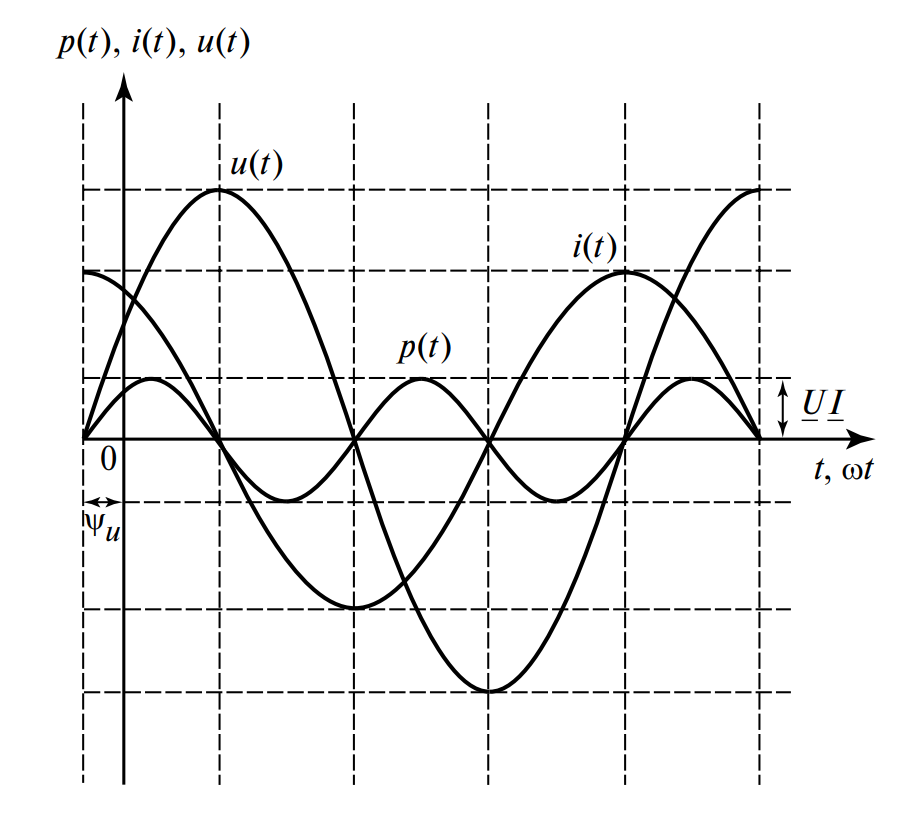
Графики тока, напряжения и мощности в емкостном элементе

Рисунок 1. Временные диаграммы.

Зависимости u(t), i(t) и р(t) для идеального емкостного элемента.

На Рисунке 1 показаны кривые:

— $ u(t) $ (напряжение);

— $ i(t) $ (ток), который достигает максимума раньше напряжения на четверть периода;

— $ p(t) $ (мощность), которая колеблется относительно нуля, показывая, что конденсатор поочередно то накапливает энергию, то возвращает её в сеть.

Рисунок 2.Векторная диаграмма токов и напряжений.

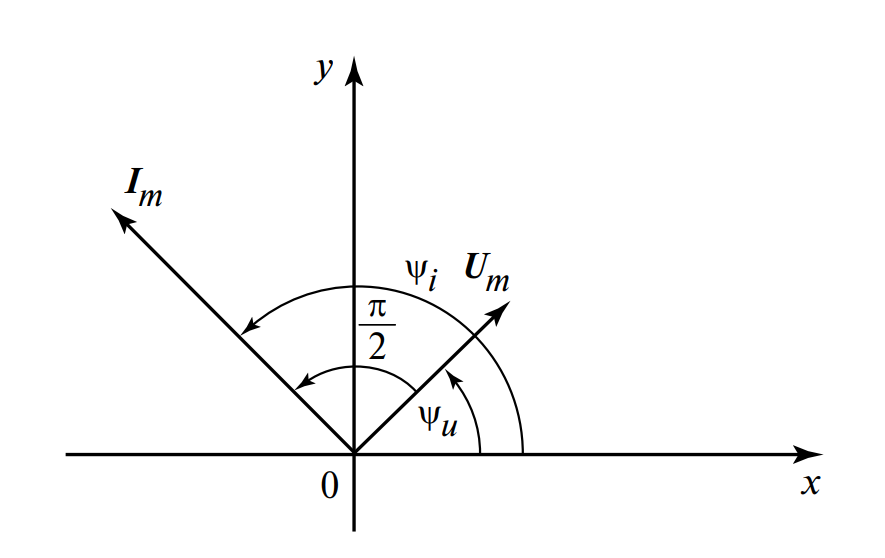
На Рисунке 2 представлена векторная диаграмма. Вектор тока $ I $ повернут относительно вектора напряжения $ U $ на угол 90° против часовой стрелки, что графически подтверждает опережение фазы.

5. Сравнительный анализ и экспертные данные

Чтобы лучше понять место емкостного элемента в теории цепей, сравним его с другими идеальными элементами.

Таблица 1. Сравнение идеальных элементов цепи

Параметр	Резистор (R)	Индуктивность (L)	Емкость (C)
Связь U и I	Закон Ома: $ U=IR $	Дифференциальная: $ u = L \frac{di}{dt} $	Дифференциальная: $ i = C \frac{du}{dt} $
Сдвиг фаз ($ \phi $)	0° (совпадают)	+90° (напряжение опережает)	-90° (ток опережает)
Зависимость от частоты	Не зависит	Растет ($ X_L = \omega L $)	Падает ($ X_C = \frac{1}{\omega C} $)
Энергия	Рассеивается (тепло)	Накапливается (магнитное поле)	Накапливается (электрическое поле)

Преимущества и недостатки в цепях переменного тока

Преимущества:

Компенсация реактивной мощности: Конденсаторы генерируют реактивную мощность, компенсируя индуктивную нагрузку двигателей, что повышает косинус фи ($ \cos \phi $) сети.
Частотная селекция: Благодаря зависимости $ X_C $ от частоты, используются в фильтрах для отсеивания низких или высоких частот.
Отсутствие нагрева: В идеальном случае не потребляют активной мощности.

Недостатки (реальных элементов):

Наличие токов утечки через диэлектрик (потери).
Возможность пробоя при перенапряжениях.
Переходные процессы с большими бросками тока при включении в сеть.

Нормативная база:
При работе с документацией и схемами следует руководствоваться действующими стандартами:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Определяет понятие «Емкостный элемент».
ГОСТ 2.728-74 «Обозначения условные графические в схемах. Резисторы, конденсаторы». Регламентирует, как правильно изображать конденсаторы на схемах.

6. 7 Интересных фактов о емкости

Ток проводимости через диэлектрик конденсатора не течет. То, что мы называем током в цепи конденсатора, Максвелл назвал «током смещения» — это скорость изменения электрического поля.
Единица измерения Фарад — это огромная величина. Емкостью в 1 Фарад обладал бы уединенный металлический шар радиусом 9 миллионов километров (это в 13 раз больше радиуса Солнца). На практике мы используем микро-, нано- и пикофарады.
Суперконденсаторы (ионисторы) могут иметь емкость в тысячи фарад в объеме пивной банки, но работают на низких напряжениях.
В линиях электропередач провода образуют паразитную емкость с землей, что вызывает зарядные токи даже при отсутствии нагрузки в конце линии.
Человеческое тело обладает емкостью относительно земли (порядка 100-200 пФ), что используется в работе сенсорных экранов.
Идеальный конденсатор при подключении к источнику постоянного идеального напряжения вызвал бы бесконечный ток в первый момент времени.
Сдвиг фаз на 90 градусов используется для создания вращающегося магнитного поля в однофазных асинхронных двигателях (конденсаторный пуск).

7. Часто задаваемые вопросы (FAQ)

1. Почему ток опережает напряжение, а не наоборот?

Это связано с физикой накопления заряда. Чтобы напряжение на обкладках конденсатора выросло, на них сначала должен «притечь» заряд. Ток — это и есть процесс притока заряда. Следовательно, сначала появляется ток (причина), и лишь по мере накопления заряда растет напряжение (следствие).

2. Чему равно активное сопротивление идеального конденсатора?

Активное сопротивление $ R $ идеального конденсатора равно нулю. У него есть только реактивное емкостное сопротивление $ X_C $. В реальных конденсаторах существует малое активное сопротивление (ESR), вызывающее нагрев.

3. Что будет, если подать на конденсатор напряжение очень высокой частоты?

Так как $ X_C = 1/(\omega C) $, при росте частоты сопротивление стремится к нулю. Для очень высоких частот конденсатор представляет собой практически короткое замыкание.

4. Потребляет ли конденсатор электричество из розетки?

Бытовой счетчик считает активную энергию. Идеальный конденсатор её не потребляет (он берет энергию, хранит её четверть периода и возвращает обратно). Однако он нагружает провода реактивным током, что плохо для электросетей.

5. Откуда берется формула $ \psi_i = \psi_u + \pi/2 $?

Она выводится математически из производной синуса: $ (sin(x))’ = cos(x) = sin(x + 90^\circ) $. Поскольку ток пропорционален производной напряжения, его фаза сдвигается на +90 градусов.

Заключение

В данном материале мы подробно рассмотрели поведение идеального емкостного элемента в цепи синусоидального тока. Мы выяснили, что емкость оказывает переменному току сопротивление, которое уменьшается с ростом частоты, и создает фазовый сдвиг, при котором ток опережает напряжение на 90°. Отсутствие потерь активной мощности делает конденсатор идеальным накопителем энергии, а не потребителем. Понимание этих процессов является базой для расчетов любых сложных цепей переменного тока, от бытовой электропроводки до сложных микропроцессорных систем.

Список литературы

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2023.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — Л.: Энергоиздат, 1981.
Зевеке Г.В., Ионкин П.А. Основы теории цепей. — М.: Энергия, 1975.
ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий.