Резонанс при несинусоидальных ЭДС: анализ гармоник в RLC-цепи

Содержание страницы

Анализ резонанса для высших гармоник
Практическое значение
Сравнение синусоидального и несинусоидального резонанса
Интересные факты по теме
FAQ (Часто задаваемые вопросы)
Заключение

Резонанс при несинусоидальных ЭДС — это комплексное явление в электрических цепях (как правило, RLC-контурах), при котором резонансные условия могут выполняться не для всего сигнала в целом, а для его отдельных гармонических составляющих (гармоник).

Исторически, анализ резонанса проводился для идеализированных синусоидальных сигналов. Однако с развитием силовой электроники, преобразовательной техники (выпрямителей, инверторов) и широким распространением импульсных источников питания в XX веке, форма тока и напряжения в сетях стала существенно отличаться от синусоиды. Это потребовало применения методов гармонического анализа (разложения в ряд Фурье) для изучения режимов работы цепей, что и привело к изучению феномена резонанса для отдельных гармоник.

Анализ резонанса для высших гармоник

Особенность резонансных явлений в цепях с несинусоидальными источниками ЭДС и токами заключается в их многогранности. Несинусоидальный сигнал представляет собой сумму синусоидальных колебаний с разными, кратным основной, частотами. Это приводит к тому, что в одной и той же цепи могут возникать резонансы для отдельных гармоник при различных условиях.

Рассмотрим в качестве примера последовательный RLC-контур, к которому подключен источник несинусоидальной ЭДС. Допустим, эта ЭДС состоит из трех гармоник (первой, второй и третьей). Схема такой цепи показана на рис. 1а.

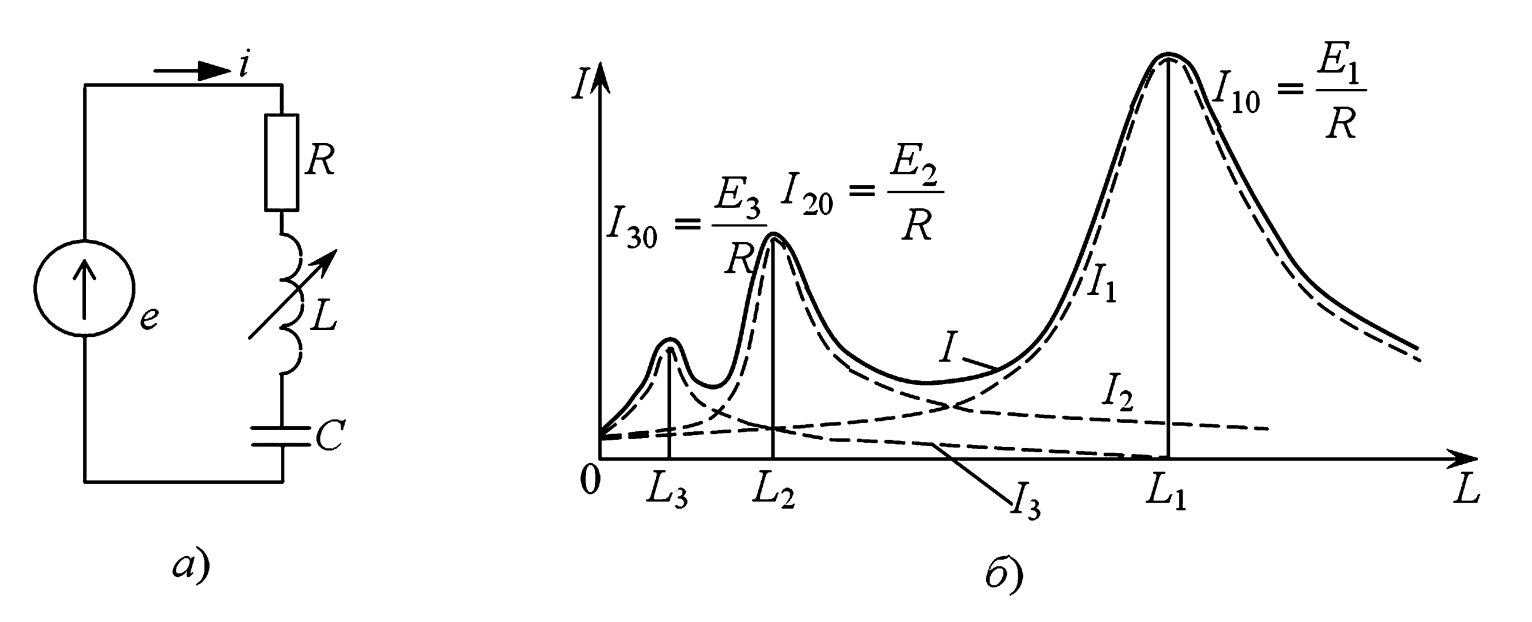
Рисунок 1. Резонанс в цепи с несинусоидальной ЭДС:
а — принципиальная схема последовательного RLC-контура;
б — качественный график зависимости общего тока I и его гармоник (I₁, I₂, I₃) от величины индуктивности L.

Расчет тока для k-й гармоники

Общий ток в цепи является суммой токов отдельных гармоник. Для k-й гармоники (где k — номер гармоники) действующее значение тока $I_k$ определяется по закону Ома для цепи переменного тока, учитывая, что частота k-й гармоники в k раз выше основной:

$$ I_k = \frac{E_k}{\sqrt{R^2 + (X_{Lk} — X_{Ck})^2}} = \frac{E_k}{\sqrt{R^2 + (k\omega L — \frac{1}{k\omega C})^2}} $$

Где:

$I_k$ — действующее значение тока k-й гармоники.
$E_k$ — действующее значение ЭДС k-й гармоники.
$R$ — активное сопротивление.
$L$ — индуктивность.
$C$ — емкость.
$\omega$ — угловая частота первой (основной) гармоники.

Условие резонанса для гармоники

Проанализируем, как будет меняться ток при изменении одного из параметров цепи, например, индуктивности $L$, в диапазоне от нуля до бесконечности.

Для каждой k-й гармоники наступит свой собственный резонанс напряжений, когда ее индуктивное сопротивление $X_{Lk} = k\omega L$ станет равно емкостному $X_{Ck} = \frac{1}{k\omega C}$. Условие резонанса для k-й гармоники:

$$ k\omega L_k = \frac{1}{k\omega C} $$

Отсюда можно найти значение индуктивности $L_k$, при котором k-я гармоника войдет в резонанс:

$$ L_k = \frac{1}{k^2 \omega^2 C} $$

Вывод: Значения индуктивности $L_k$, необходимые для резонанса, обратно пропорциональны квадрату номера гармоники (k²). Это означает, что резонанс для высших гармоник (k=3, 5, 7…) наступит при значительно меньших значениях индуктивности, чем для основной (k=1).

В момент резонанса (при $L = L_k$) полное сопротивление цепи для k-й гармоники становится минимальным и равным активному сопротивлению $R$. Соответственно, ток этой гармоники достигает своего максимума:

$$ I_{k, \text{max}} = \frac{E_k}{R} $$

Анализ графика общего тока

Этот процесс наглядно иллюстрирует рис. 1б. Пунктирными линиями показаны резонансные кривые для трех гармоник тока ($I_1$, $I_2$, $I_3$). Каждая кривая имеет свой максимум при своем значении $L_k$.

Общий действующий ток в цепи (тот, который измерит амперметр) определяется как среднеквадратичное значение суммы гармоник:

$$ I = \sqrt{I_1^2 + I_2^2 + I_3^2 + \ldots} $$

Сплошная линия на рис. 1б показывает этот общий ток. Если активное сопротивление $R$ в цепи достаточно мало (что обеспечивает высокую добротность контура), то пики отдельных гармоник будут ярко выражены. В результате кривая общего тока будет иметь несколько максимумов (в данном примере — три), каждый из которых соответствует резонансу одной из гармоник.

Стоит отметить, что аналогичная картина (возникновение множественных резонансов) будет наблюдаться и при изменении других параметров контура, например, емкости C (резонансные значения будут $C_k = \frac{1}{k^2 \omega^2 L}$) или частоты $\omega$. Последнее, однако, справедливо только в том случае, если при изменении частоты форма кривой ЭДС (т.е. состав и соотношение ее гармоник) остается неизменной.

Практическое значение

Явление резонанса при несинусоидальных сигналах имеет как положительные, так и отрицательные аспекты.

Практическое применение

Фильтрация сигналов: Это свойство широко используется при проектировании электрических фильтров. Настраивая RLC-контур в резонанс с определенной гармоникой, можно ее усилить (в полосовых фильтрах) или, наоборот, подавить (в заграждающих фильтрах). Это критически важно в радиотехнике, связи и аудиотехнике для очистки сигнала от нежелательных гармоник.

Опасность явления

Аварийные режимы в силовых сетях: В промышленных электрических сетях несинусоидальные токи (например, от мощных выпрямителей, сварочных аппаратов, частотных преобразователей) могут вызвать непреднамеренный резонанс на одной из высших гармоник (часто 5-й, 7-й, 11-й). Это приводит к резкому возрастанию токов и напряжений на элементах цепи (кабелях, конденсаторных батареях для компенсации реактивной мощности, трансформаторах), вызывая их перегрев, преждевременное старение изоляции и даже разрушение.

Сравнение синусоидального и несинусоидального резонанса

Параметр	Классический (синусоидальный) резонанс	Несинусоидальный резонанс (резонанс гармоник)
Источник сигнала	Идеальная синусоида (одна частота $\omega$)	Несинусоидальный сигнал (сумма гармоник $k\omega$)
Условие резонанса	$\omega L = 1/(\omega C)$	$k\omega L = 1/(k\omega C)$ (для k-й гармоники)
Количество резонансных точек	Одна резонансная частота (или одно значение L/C)	Множество резонансных точек (по одной для каждой гармоники)
Форма тока в контуре	Синусоидальная, резко возрастает в амплитуде	Сложная, несинусоидальная. Резко возрастает амплитуда одной из гармоник
Практическое значение	Настройка радиоприемников, фильтры	Фильтрация гармоник, причина аварий в силовых сетях

Интересные факты по теме

«Музыкальные» гармоники: Понятие гармоник в электротехнике полностью аналогично музыкальным обертонам, которые и определяют тембр звука. Резонанс гармоник в электроцепи — это, по сути, «выделение» одного из обертонов электрического сигнала.
Опасность для «нуля»: В трехфазных сетях токи основной гармоники в нулевом проводе взаимно компенсируются. Однако токи высших гармоник, кратных трем (3, 9, 15…), не компенсируются, а складываются в нулевом проводе, что может вызвать его опасный перегрев.
Виновники гармоник: Основными «генераторами» высших гармоник в современных сетях являются нелинейные нагрузки: компьютеры (импульсные блоки питания), светодиодные лампы (драйверы) и частотные преобразователи электродвигателей.
Феррорезонанс: Существует еще более сложный вид несинусоидального резонанса — феррорезонанс. Он возникает в цепях с нелинейной индуктивностью (например, трансформатором с насыщенным сердечником) и емкостью.
Цифровой анализ: Для точного анализа несинусоидальных режимов сегодня вместо рядов Фурье часто используют Быстрое преобразование Фурье (БПФ) — алгоритм, реализованный в большинстве современных анализаторов качества электроэнергии.

FAQ (Часто задаваемые вопросы)

1. Почему при несинусоидальном токе может быть несколько резонансов?

Потому что несинусоидальный сигнал состоит из множества синусоидальных сигналов (гармоник) с разными частотами ($\omega, 2\omega, 3\omega, \ldots$). Каждая из этих гармоник может войти в резонанс с контуром L и C при разных условиях (например, при разных значениях L), что создает несколько пиков тока.

2. Как найти индуктивность, при которой 5-я гармоника войдет в резонанс?

Нужно использовать формулу $L_k = 1 / (k^2 \omega^2 C)$. Подставив $k=5$, получим $L_5 = 1 / (25 \omega^2 C)$, где $\omega$ — частота основной (первой) гармоники.

3. Чем опасен резонанс высших гармоник в силовой сети?

Он опасен резким, неконтролируемым ростом тока и напряжения на частоте этой гармоники. Это приводит к перегреву кабелей, пробою изоляции, выходу из строя конденсаторных батарей и трансформаторов, даже если общая (полная) нагрузка кажется номинальной.

4. Что показывает амперметр в цепи с несинусоидальным током?

Амперметр (тепловой или электромагнитной системы, или цифровой с функцией True RMS) показывает общее действующее значение тока, которое вычисляется по формуле $I = \sqrt{I_1^2 + I_2^2 + I_3^2 + \ldots}$. Он не показывает, какая из гармоник вносит наибольший вклад.

5. Можно ли использовать резонанс гармоник с пользой?

Да. На этом принципе работают пассивные фильтры гармоник. Например, для подавления 5-й гармоники в цепь устанавливают контур, настроенный в резонанс на частоту этой гармоники (250 Гц для сети 50 Гц), который «отводит» ток этой гармоники на себя, очищая остальную сеть.

Заключение

Таким образом, резонанс в цепях с несинусоидальными сигналами — это комплексное явление, требующее применения гармонического анализа. В отличие от простого синусоидального режима, в RLC-контуре может возникать не один, а несколько резонансных пиков, соответствующих разным гармоникам. Понимание того, что каждая гармоника может входить в резонанс независимо от других, является ключевым для проектирования помехоподавляющих фильтров и обеспечения надежности и безопасности работы современных силовых электрических сетей.

Нормативные документы

ГОСТ 32144-2013 «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения» (Регламентирует уровни гармонических составляющих в сетях).
ГОСТ 30804.4.7-2013 «Совместимость технических средств электромагнитная. Общее руководство по измерительным приборам и измерениям гармоник и интергармоник для систем электроснабжения и подключаемого к ним оборудования».