Переменный ток: Теория и расчет, получение и применение

Содержание страницы

1. Введение: Природа переменного тока
2. Физика процесса: Генерация и Закон Электромагнитной индукции
3. Классификация и временные характеристики
4. Математическая модель синусоидального тока
5. Фазовые соотношения: Синфазность, Противофаза и Квадратура
6. Количественные оценки: Действующее и Среднее значения
7. Векторные диаграммы: Инструмент профессионала
8. Сравнение методов анализа
9. Интересные факты о переменном токе
10. Часто задаваемые вопросы (FAQ)
11. Частые ошибки и заблуждения
Заключение

1. Введение: Природа переменного тока

Переменный ток (AC, Alternating Current) — это направленное движение электрических зарядов, параметры которого (сила тока, напряжение, ЭДС) изменяются во времени по определенному закону. В отличие от постоянного тока, переменный ток позволяет эффективно трансформировать уровни напряжения, что делает возможной передачу энергии на тысячи километров.

Краткая история: Теоретическая база переменных токов была заложена в XIX веке Джеймсом Клерком Максвеллом и Генрихом Герцем. Однако практическая реализация — заслуга Николы Теслы и Михаила Доливо-Добровольского (изобретателя трехфазной системы). Именно переход на переменный ток позволил создать современные энергосистемы, объединяющие города и страны.

Рисунок 1 — График постоянного и переменного (синусоидального) тока

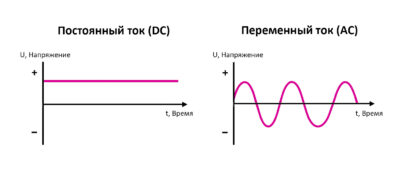
Большинство современных электротехнических устройств предназначено именно для производства, преобразования и передачи электроэнергии. Все эти инженерные задачи технически проще и экономически выгоднее решать с помощью переменных токов и напряжений.

Справка: Переменные токи возникают не только в цепях с генераторами. Они также рождаются в результате переходных процессов (коммутаций) — например, при резком включении мощного двигателя, отключении линии передач или коротком замыкании.

Аналогия с переменным током: Велосипедная цепь

Чтобы понять разницу, представьте перевернутый велосипед:

Постоянный ток (DC): Вы крутите педали как обычно — только вперед. Звенья цепи (электроны) действительно физически перемещаются от передней звездочки к задней.
Переменный ток (AC): Представьте, что вы не крутите педали по кругу, а быстро дергаете их рукой: пол-оборота вперед, пол-оборота назад.

Что происходит? Звенья цепи (электроны) никуда не уезжают, они просто «елозят» туда-сюда на 10 сантиметров. Но при этом энергия всё равно передается — заднее колесо (лампочка/нагрузка) тоже будет дергаться и крутиться.

Так и в розетке: электроны, которые «зажгли» вашу лампу, никогда не были на электростанции. Они просто колебались у вас в проводке, толкая друг друга.

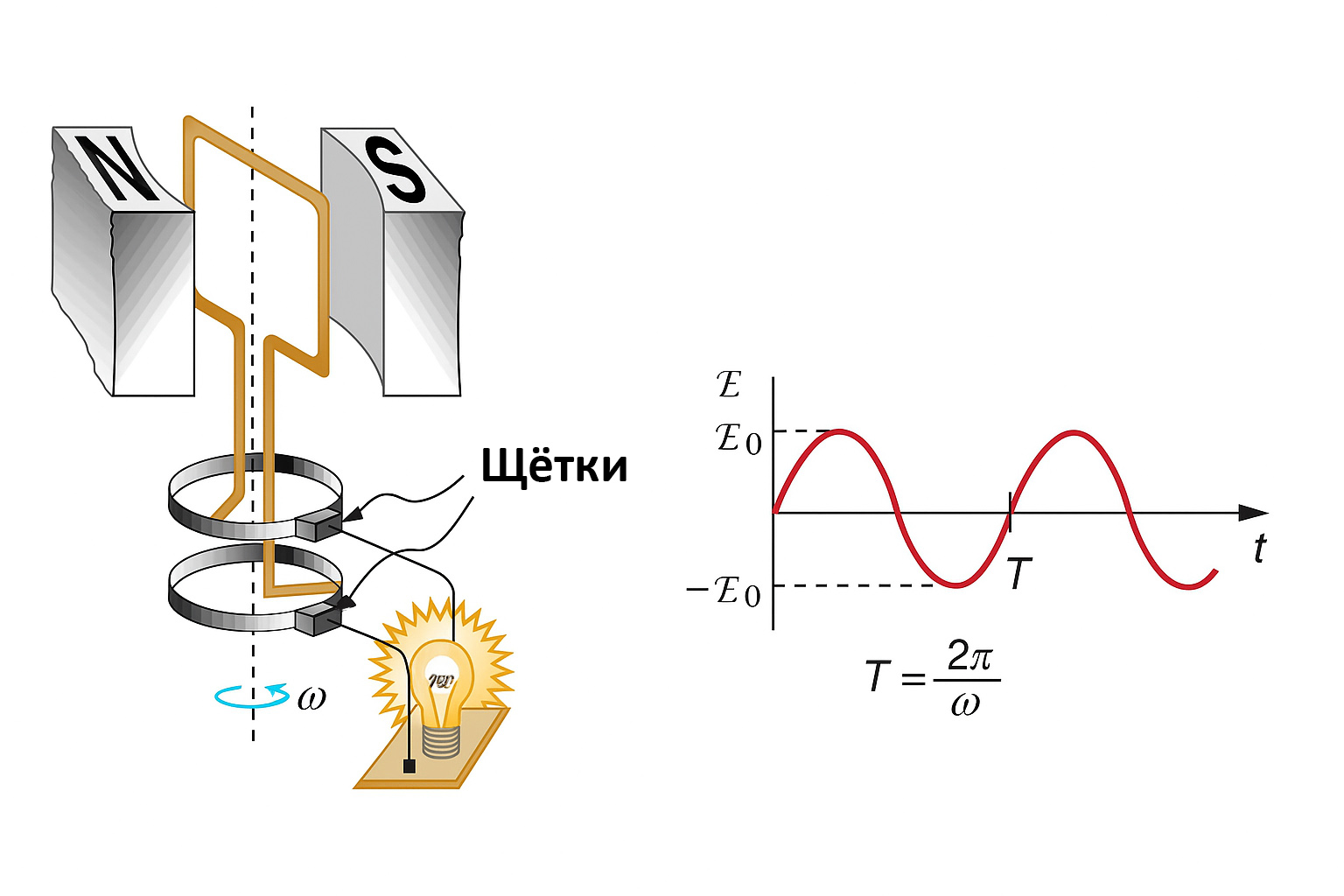
2. Физика процесса: Генерация и Закон Электромагнитной индукции

Понимание переменного тока невозможно без понимания принципа работы синхронного генератора (альтернатора), который вырабатывает переменный ток. Именно физическая конструкция генератора определяет форму тока как синусоидальную.

Закон Фарадея — Максвелла

В основе генерации лежит фундаментальный закон электромагнитной индукции, открытый Майклом Фарадеем в 1831 году. Он гласит:

«Электродвижущая сила (ЭДС), возникающая в проводящем контуре, пропорциональна скорости изменения магнитного потока, пронизывающего этот контур».

Математически это записывается так:

e(t) = -N \frac{d\Phi}{dt}

Где \( N \) — число витков в катушке, а \( \frac{d\Phi}{dt} \) — скорость изменения магнитного потока.

Механизм рождения синусоиды

Представьте простейший генератор: прямоугольная рамка вращается в однородном магнитном поле постоянного магнита.

Рисунок 2 — Простейший генератор переменного тока

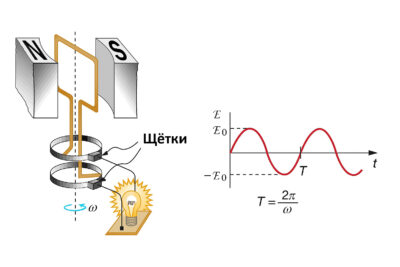
Магнитный поток (\( \Phi \)): Количество линий магнитного поля, проходящих через рамку, зависит от угла поворота \( \alpha \). Поток максимален, когда рамка перпендикулярна линиям, и равен нулю, когда она параллельна им.Формула потока: \( \Phi = B \cdot S \cdot \cos(\alpha) \)(где \( B \) — индукция поля, \( S \) — площадь рамки).
Вращение: Рамка вращается с угловой скоростью \( \omega \), поэтому угол меняется во времени: \( \alpha = \omega t \).Следовательно: \( \Phi(t) = B \cdot S \cdot \cos(\omega t) \).
Возникновение ЭДС: Согласно закону Фарадея, нам нужно найти производную потока по времени (скорость изменения). Производная от косинуса — это минус синус (\( \cos’ = -\sin \)). Физически это объясняется просто: когда рамка параллельна линиям поля (угол 90°), магнитный поток через нее равен нулю, но именно в этот момент рамка пересекает линии «наискосок» с максимальной скоростью. И наоборот: когда поток максимален (рамка перпендикулярна линиям), она на мгновение скользит вдоль них, и изменения потока почти нет. Поэтому пик ЭДС (Синус) сдвинут относительно пика Потока (Косинус).

e(t) = — \frac{d}{dt} (B S \cos(\omega t)) = B S \omega \sin(\omega t)

Рисунок 3. Графическая иллюстрация возникновения синусоидальной ЭДС при вращении рамки в магнитном поле магнита.

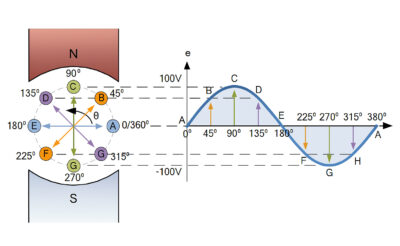
Рассмотрим диаграмму на Рисунке 3 подробнее, так как она является ключом к пониманию природы переменного тока:

Точка A (\(0^\circ\)) и E (\(180^\circ\)): Проводник движется параллельно магнитным силовым линиям. Пересечения линий не происходит, поэтому ЭДС равна нулю (\(e = 0\)).
Точка C (\(90^\circ\)): Проводник пересекает силовые линии строго перпендикулярно. В этот момент скорость изменения магнитного потока максимальна, следовательно, генерируется пиковое положительное напряжение (\(+E_{max}\)).
Точка G (\(270^\circ\)): Проводник снова пересекает линии перпендикулярно, но уже двигаясь в обратном направлении относительно поля (снизу вверх). Возникает пиковое отрицательное напряжение (\(-E_{max}\)).
Промежуточные точки (B, D, F, H): Проводник пересекает поле под углом. Значение ЭДС в эти моменты соответствует проекции вектора скорости, что и формирует плавный изгиб синусоиды.

Вывод: Мы получили уравнение \( e(t) = E_{max} \sin(\omega t) \).
Это доказывает, что синусоидальная форма напряжения — это не прихоть инженеров, а естественное следствие равномерного вращения в магнитном поле.

Правило правой руки (для определения направления индуцированного тока)

Чтобы понять, в каком направлении в данный момент будет протекать индуцированный ток в проводнике вращающейся рамки, используют правило правой руки, применяемое для процессов электромагнитной индукции (правило Флеминга).

Рисунок 4. Правило правой руки.

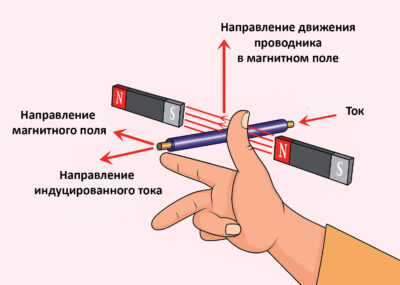
Пальцы правой руки располагают взаимно перпендикулярно:

Указательный палец направляют по магнитному полю — от Северного полюса (N) к Южному (S).
Большой палец указывает направление движения проводника относительно магнитного поля.
Средний палец показывает направление возникающего индуцированного тока.

Поскольку при вращении одна сторона рамки движется вверх, а другая — вниз, индуцированные токи в них направлены противоположно. Каждые пол-оборота (180°) стороны рамки меняются местами относительно магнитного поля, и направление тока в обмотке меняется на противоположное. Именно так формируется переменный ток.

3. Классификация и временные характеристики

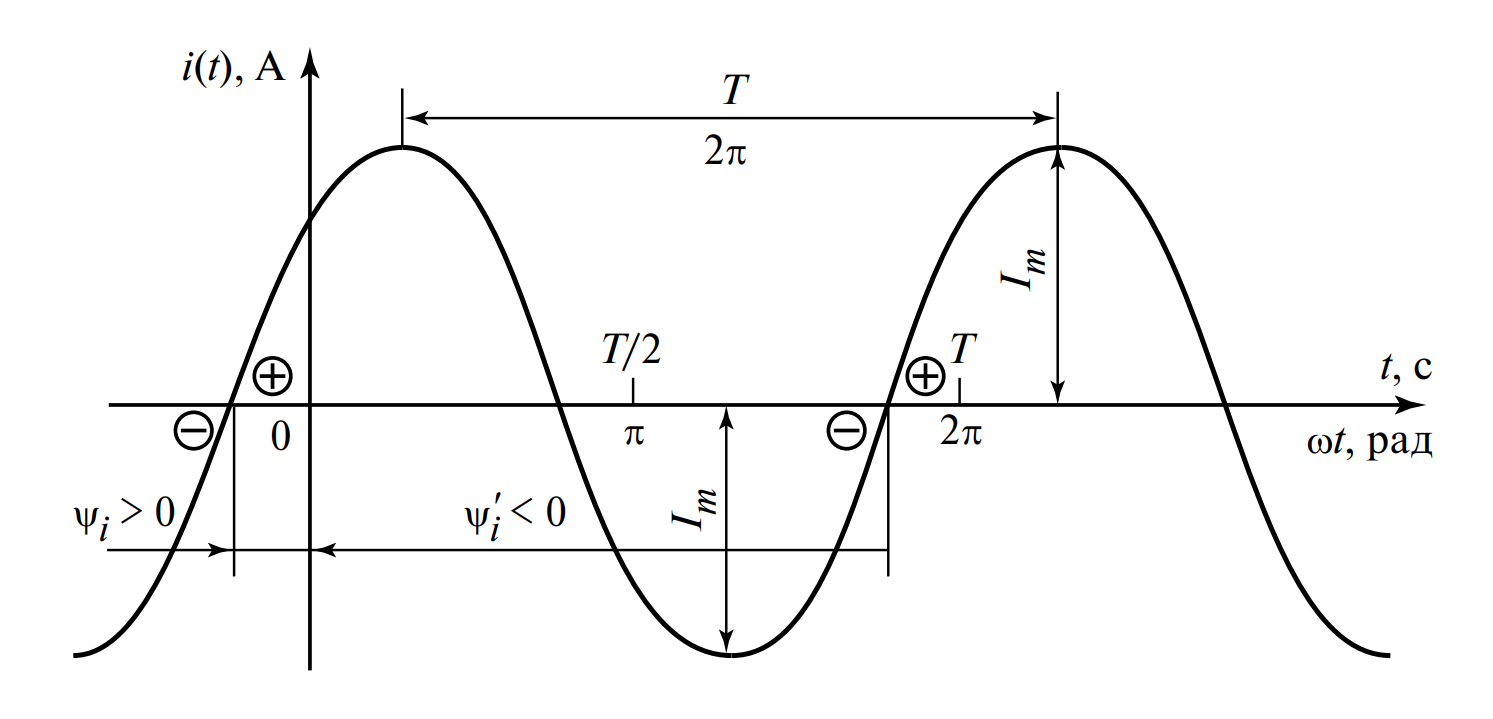
В самом широком смысле переменными называются любые токи, изменяющиеся с течением времени. Значения тока в произвольные моменты времени \( t \) называются мгновенными значениями и обозначаются строчными буквами: \( i(t) \) для тока, \( u(t) \) для напряжения и \( e(t) \) для ЭДС.

Однако хаотичные изменения токов сложны для анализа. Поэтому в технике наиболее часто применяются периодические токи, значения которых повторяются через равные промежутки времени \( T \).

Рисунок 5 — Разновидности графиков мгновенных значений периодических токов, напряжений и ЭДС

Простейшим и самым важным видом периодического тока является синусоидальный ток. Именно он используется в стандартных розетках и промышленных сетях, так как обеспечивает наиболее экономичные режимы работы оборудования (минимальные потери в трансформаторах и двигателях).

4. Математическая модель синусоидального тока

Для инженера недостаточно просто сказать «ток меняется». Необходимо точное математическое описание. Мгновенные значения синусоидальных величин описываются следующими тригонометрическими функциями:

i(t) = I_m \sin (\omega t + \psi_i) \) \( u(t) = U_m \sin (\omega t + \psi_u) \) \( e(t) = E_m \sin (\omega t + \psi_e)

Где:

\( I_m, U_m, E_m \) — амплитудные значения (максимально возможные значения модуля величины).
\( (\omega t + \psi) \) — текущая фаза (аргумент синуса).
\( \psi_i, \psi_u, \psi_e \) — начальные фазы (значение фазы в момент времени \( t=0 \)).

Рисунок 6 — Основные параметры синусоиды во временной области

Частотные характеристики

Ключевым параметром является угловая частота \( \omega \) (омега). Она связывает время и угол поворота вектора генератора.

\omega = 2\pi f = \frac{2\pi}{T}

Где \( T \) — период (время одного полного колебания), а \( f \) — частота (число колебаний в секунду).

Стандартизация частот:

50 Гц: Стандарт энергетических систем РФ (ГОСТ 29322-2014) и большинства стран Европы и Азии.
60 Гц: Стандарт США, Канады, некоторых стран Южной Америки.
400 Гц, 1000 Гц: Используются в авиации (самолеты, вертолеты) и на морских судах. Повышение частоты позволяет существенно уменьшить габариты и вес трансформаторов и двигателей, что критично для транспорта.

Как почувствовать 50 Гц?

Звук: Если дотронуться пальцем до входного штекера включенных колонок, вы услышите низкий гул. Это и есть «звучание» переменного тока сети — 50 колебаний в секунду (нота где-то между «Соль» и «Соль-диез» контроктавы).
Видео: Наведите камеру смартфона на старую уличную лампу или светодиодную гирлянду. Вы увидите бегущие темные полосы. Это происходит из-за того, что частота съемки камеры не совпадает с частотой мерцания лампы (100 вспышек в секунду).

5. Фазовые соотношения: Синфазность, Противофаза и Квадратура

В реальных цепях переменного тока напряжение и ток редко совпадают по фазе. Разность их начальных фаз \( \varphi = \psi_u — \psi_i \) называется сдвигом фаз. Эта величина определяет характер нагрузки и напрямую влияет на реактивную мощность, угол мощности и коэффициент мощности (\( \cos\varphi \)).

Условие	Термин	Физический смысл
\( \psi_u — \psi_i = 0 \)	Синфазность	Ток и напряжение проходят через ноль и достигают максимума одновременно. Нагрузка потребляет только активную мощность. Пример: чисто резистивный элемент (ТЭН, лампа накаливания).
\( \psi_u — \psi_i = \pm 180^\circ (\pm \pi) \)	Противофаза	Ток имеет противоположное направление относительно напряжения: максимум тока приходится на минимум напряжения. Физически эквивалентно резистору, но с инвертированным направлением тока (например, при изменении знака ЭДС).
\( \psi_u — \psi_i = \pm 90^\circ (\pm \pi/2) \)	Квадратура	Сдвиг на четверть периода. В этой точке ток не потребляет активной мощности, а лишь обменивается энергией с полем. Ток отстаёт на 90° в чистой индуктивности и опережает напряжение на 90° в идеальной ёмкости.

Если \( \psi_u — \psi_i > 0 \), говорят, что напряжение опережает ток — характерно для индуктивной нагрузки, где энергия накапливается в магнитном поле.
Если \( \psi_u — \psi_i < 0 \), ток опережает напряжение — это свойственно ёмкостным нагрузкам, где энергия временно хранится в электрическом поле.

Аналогия: Напряжение и Качели (Ёмкость)

Многих сбивает с толку термин «опережение». Как ток может опережать напряжение, если напряжение — причина тока?

Представьте, что вы раскачиваете качели. Чтобы они пошли вниз, вы должны начать давить на них раньше, когда они еще находятся в верхней точке и на мгновение замерли. Ваше усилие (Напряжение) и движение качелей (Ток) сдвинуты по времени.

В конденсаторе ток (движение зарядов) начинается до того, как на обкладках вырастет напряжение.

Аналогия: Ток как вода

Представьте тяжелое водяное колесо (это индуктивность).

Вы резко открыли заслонку и подали напор воды (это Напряжение — оно уже есть, максимум).
Но колесо тяжелое, оно не может раскрутиться мгновенно. Поток воды (это Ток) нарастает плавно, по мере разгона колеса.

Именно поэтому в индуктивности ток «опаздывает» за напряжением. Энергия тратится на создание магнитного поля (раскрутку колеса).

6. Количественные оценки: Действующее и Среднее значения

Переменный ток непрерывно меняется, поэтому судить о его «силе» по мгновенному значению в конкретную миллисекунду неудобно. Инженерам нужны понятные величины для расчетов. В электротехнике используют две основные оценки: действующее и среднее значения.

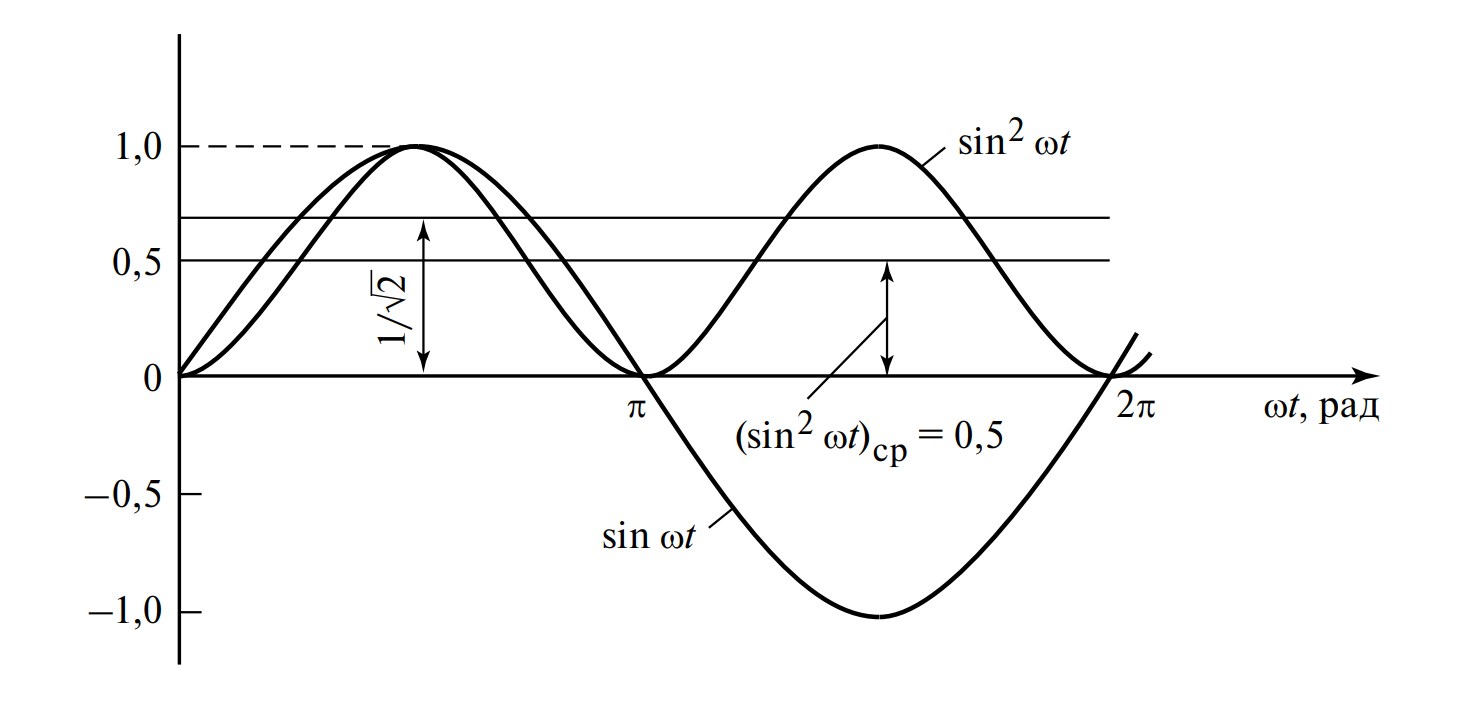
6.1. Действующее (среднеквадратичное) значение (RMS)

Это главная характеристика переменного тока в энергетике. Действующее значение (Root Mean Square) численно равно величине такого постоянного тока, который за время одного периода \( T \) выделит в том же самом резисторе \( R \) такое же количество теплоты \( Q \), что и данный переменный ток.

Математический вывод формулы через интеграл (на основании закона Джоуля-Ленца):

I = \sqrt{\frac{1}{T} \int_{0}^{T} i^2(t) \, dt}

Для синусоидального тока интеграл от квадрата синуса дает коэффициент \( \sqrt{2} \):

I = \frac{I_m}{\sqrt{2}} \approx 0,707 I_m

Аналогично для напряжения и ЭДС: \( U = U_m / \sqrt{2} \), \( E = E_m / \sqrt{2} \).

Рисунок 7 — Синусоида, квадрат синусоиды и графическое определение действующего значения

Внимание! Все бытовые и промышленные вольтметры/амперметры по умолчанию показывают действующее значение. Когда говорят «напряжение в розетке 220 В», имеют в виду именно RMS. Амплитуда (пик) при этом составляет \( 220 \cdot \sqrt{2} \approx 311 \) В.

Пример из жизни: Почему взрываются конденсаторы?

Вы собираете схему и покупаете конденсатор с маркировкой 250 Вольт. Казалось бы, для сети 220 В запаса хватает? Нет!

220 В — это действующее значение (тепловой эквивалент). А изоляцию конденсатора пробивает амплитудное напряжение (верхушка синусоиды). В сети 220 В оно достигает \( 311 \) Вольт.

Конденсатор на 250 В выйдет из строя практически мгновенно. Для надежной работы в сети 220 В нужно выбирать компоненты с запасом по напряжению минимум 400 В.

6.2. Среднее значение

Вторая важная метрика — это простое математическое среднее.

I_{0} = \frac{1}{T} \int_{0}^{T} i(t) \, dt

Если мы попробуем посчитать среднее значение для чистой синусоиды за полный период, мы получим ноль (\( I_{0} = 0 \)). Это логично: площадь верхней полуволны (положительный заряд) равна площади нижней (отрицательный заряд), и в сумме они компенсируют друг друга.

Однако в технике (особенно в выпрямителях) используют средневыпрямленное значение (среднее по модулю) — как если бы нижнюю полуволну «зеркально» отобразили наверх:

I_{\text{ср.мод}} = \frac{2}{\pi} I_m \approx 0,637 I_m

6.3. Шпаргалка: Что и когда использовать?

Новичков часто путает наличие двух разных значений. Чтобы не ошибиться, используйте простую классификацию:

Тип значения	Действующее (RMS) \( \approx 0,707 I_{max} \)	Среднее (по модулю) \( \approx 0,637 I_{max} \)
Физический смысл	Энергия и Тепло	Заряд и Масса вещества
Где применяется	Расчет мощности двигателей и нагревателей. Выбор сечения проводов (чтобы не расплавились). Большинство измерительных приборов (мультиметры).	Зарядка аккумуляторов (важно количество перенесенного заряда). Гальваника (сколько металла осядет на электроде). Расчет выпрямительных диодов.

7. Векторные диаграммы: Инструмент профессионала

Расчет сложных разветвленных цепей с использованием тригонометрических уравнений (синусов и косинусов) крайне трудоемок и громоздок. Инженерная практика использует метод вращающихся векторов (векторные диаграммы) и комплексных чисел.

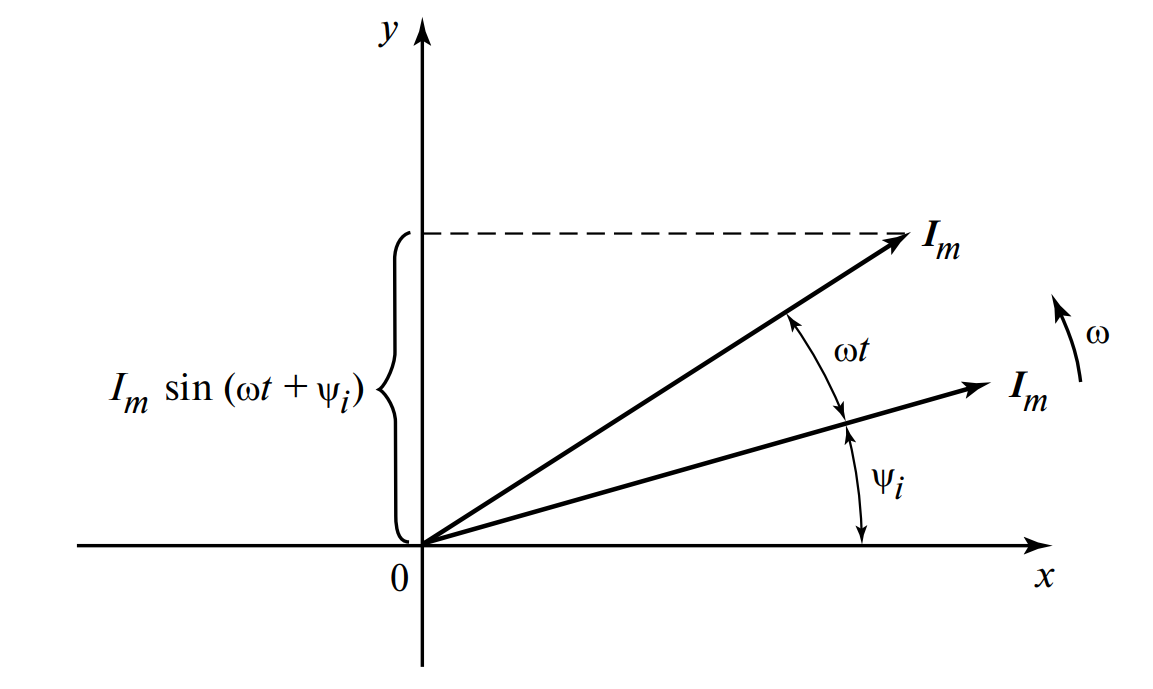
Принцип построения

Синусоидальную величину можно представить как проекцию вектора, вращающегося против часовой стрелки с частотой \( \omega \).

Длина вектора берется равной амплитуде \( I_m \) (или действующему значению \( I \)).
Вектор располагают на плоскости под углом к горизонтальной оси \( 0x \), равным начальной фазе \( \psi \).
При вращении вектора его проекция на ось \( 0y \) (ординат) чертит синусоиду.

Рисунок 8 — Генезис синусоиды: связь вращающегося вектора и временного графика

Сложение токов и напряжений

Главное преимущество метода: сложение двух синусоидальных колебаний заменяется геометрическим сложением векторов.

- Правило треугольника (цепочки): К концу вектора \( \vec{A} \) пристраиваем начало вектора \( \vec{B} \). Результат — вектор, соединяющий начало первого с концом второго.
- Правило параллелограмма: Векторы \( \vec{A} \) и \( \vec{B} \) выходят из одной точки. Строим на них параллелограмм. Диагональ — сумма векторов.

Рисунок 9 — Графическая реализация сложения векторов A + B + C = D

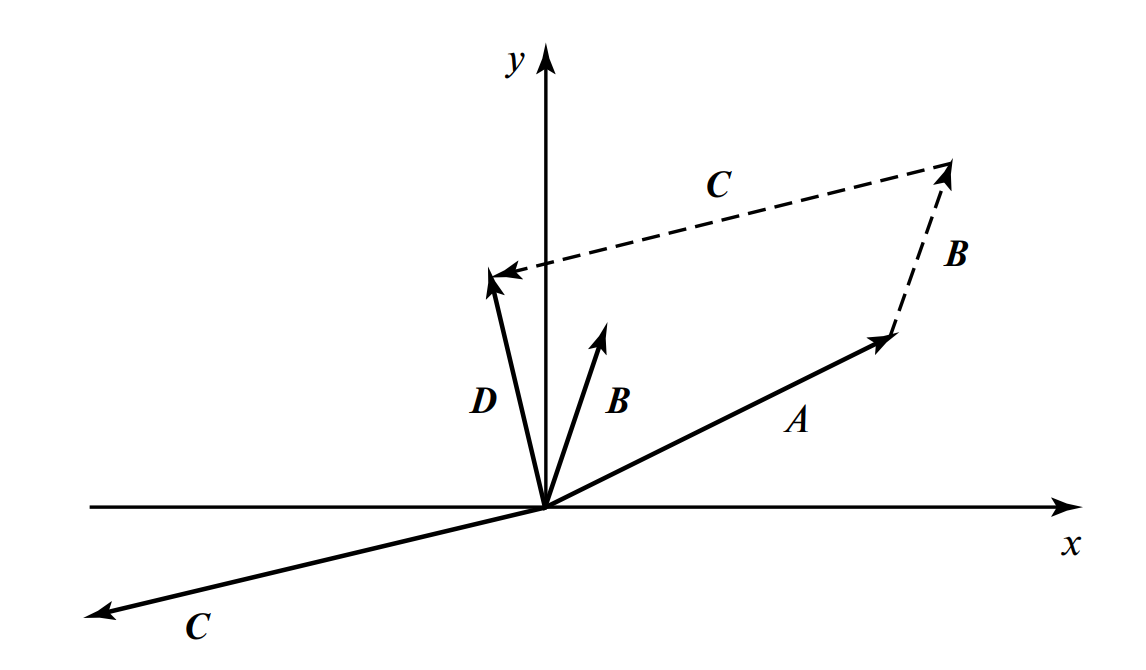
Вычитание векторов \( \vec{N} = \vec{A} — \vec{B} \) производится соединением концов векторов, причем стрелка результирующего вектора направлена к уменьшаемому (к вектору A).

[Рисунок 6: ]

Рисунок 10 — Векторные операции: сложение (M) и вычитание (N)

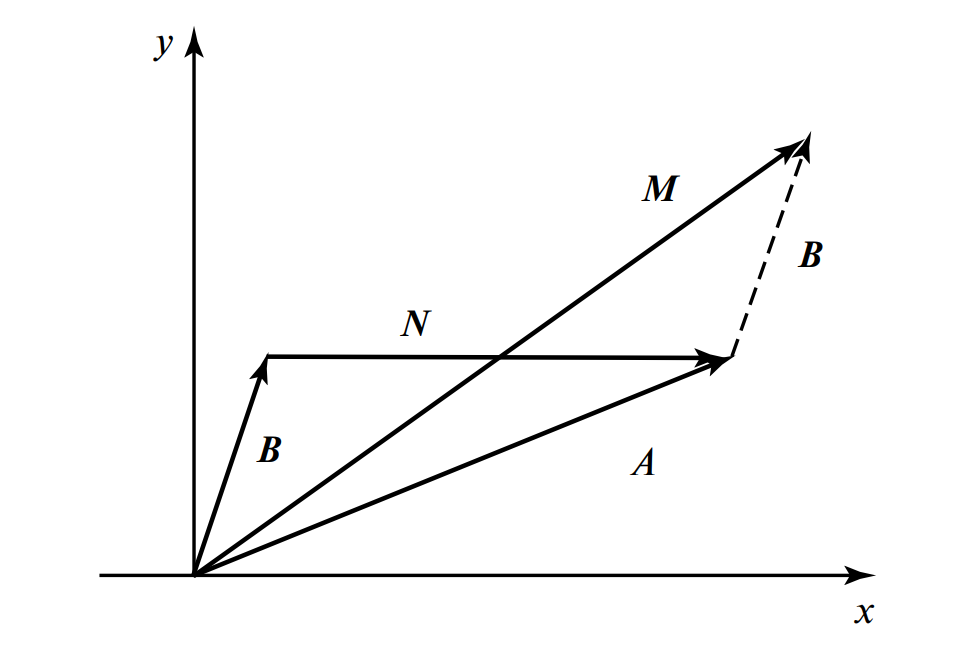
Параллелограмм векторов A и B. Диагональ M — сумма. Вектор N, соединяющий концы — разность.

8. Сравнение методов анализа

Для закрепления материала сравним подходы к описанию переменного тока.

Метод	Мгновенные значения (Временная область)	Векторные диаграммы / Комплексный метод
Инструментарий	Тригонометрия, формулы \( \sin(\alpha + \beta) \)	Геометрия, комплексные числа \( A e^{j\psi} \)
Наглядность	Показывает физический процесс в динамике	Показывает соотношения фаз и амплитуд статично
Сложность расчетов	Очень высокая для цепей с N > 2 элементами	Низкая, сводится к алгебре
Применение	Анализ нелинейных цепей, выпрямителей	Расчет линейных цепей, ЛЭП, трансформаторов

9. Интересные факты о переменном токе

Действующее значение — этот термин возник из необходимости продавать электроэнергию. Нужно было уравнять «полезность» переменного тока с постоянным для расчетов за освещение.
Векторные диаграммы «вращаются» в голове инженера со скоростью 3000 оборотов в минуту (для 50 Гц), но рисуем мы их неподвижными, словно под стробоскопом.
Коэффициент \( \sqrt{2} \) справедлив только для идеальной синусоиды. Для квадратной волны (меандр) действующее значение равно амплитудному.
400 Гц в авиации используется потому, что трансформатор на 400 Гц весит почти в 8 раз меньше аналога на 50 Гц при той же мощности.
Трехфазный ток — это система из трех векторов, сдвинутых на 120°. Главная «магия» не в сумме нулей, а в том, что три неподвижные катушки, расположенные по кругу, создают вращающееся магнитное поле. Именно оно крутит роторы асинхронных двигателей без всяких щеток и магнитов. Это основа всей мировой промышленности.
Скин-эффект — явление, при котором переменный ток высокой частоты течет только по поверхности проводника, не проникая вглубь.
«Косинус фи» (\( \cos \varphi \)) — это ключевой показатель эффективности предприятия, показывающий соотношение активной и полной мощности.

10. Часто задаваемые вопросы (FAQ)

В1: Почему используется именно синус, а не косинус?

О: Это вопрос соглашения о начале отсчета времени. Форма волны одна и та же. Если начать отсчет с максимума — будет косинус. В электротехнике принято начинать отсчет с момента перехода через ноль вверх, поэтому — синус.

В2: Зачем нужны комплексные числа при расчете тока?

О: Комплексные числа — это алгебраический способ записи векторов. Они позволяют заменить сложение синусоид сложением координат векторов, что намного проще.

В3: Что такое «Квадратура» простыми словами?

О: Это состояние, когда один процесс достигает пика ровно в тот момент, когда второй проходит через ноль. Это сдвиг на 90 градусов.

В4: Опаснее ли переменный ток постоянного?

О: При низких напряжениях (до 500 В) переменный ток 50 Гц опаснее, так как вызывает фибрилляцию сердца. При очень высоких напряжениях постоянный ток опаснее из-за возникновения устойчивой электрической дуги.

В5: В чем разница между I и i(t)?

О: Маленькая \( i(t) \) — это значение тока прямо сейчас (мгновенное). Большая \( I \) — это усредненная характеристика (действующее значение), которую показывает прибор.

11. Частые ошибки и заблуждения

Движение электронов — многие думают, что электроны бегут по проводам от электростанции к розетке. На самом деле в переменном токе они лишь колеблются на месте «туда-сюда», передавая энергию по цепочке, как в «колыбели Ньютона».
Траектория движения — глядя на график синусоиды, новички часто представляют, что электроны внутри провода физически двигаются по волнистой линии (змейкой). Это иллюзия! Электроны в проводе колеблются строго линейно (вперед-назад). Синусоида — это не путь электрона в пространстве, а график изменения его параметров во времени.
Скорость тока — многие путают скорость распространения электрического поля (близка к скорости света, 300 000 км/с) со скоростью движения самих электронов (дрейфовая скорость). В проводах вашей комнаты электроны движутся поразительно медленно — доли миллиметра в секунду. Лампочка загорается мгновенно не потому, что электрон добежал от выключателя, а потому что электромагнитное поле толкнуло все электроны в цепи одновременно.
Трансформатор — не способен изменять частоту тока. Это распространенная ошибка новичков: трансформатор меняет напряжение и ток, но если на входе 50 Гц, на выходе всегда останется 50 Гц.
Мерцание света — хотя ток проходит через ноль 100 раз в секунду (при 50 Гц), лампочка не успевает полностью погаснуть. Тепловая инерция нити накаливания или послесвечение люминофора сглаживают эти провалы для человеческого глаза.
Генератор — не «рождает» электричество. Он работает как насос: генератор не создает заряды, а лишь заставляет двигаться уже существующие свободные электроны внутри проводника.

Заключение

Рассмотрение природы переменного тока через призму математического анализа — необходимый шаг для перехода от любительской электрики к профессиональной электротехнике. Мы разобрали, как хаотичное на первый взгляд движение электронов описывается строгими законами гармонических функций и векторной алгебры.

Векторные диаграммы позволяют визуализировать сложные процессы в цепях, а интегральное исчисление дает точное понимание энергетических характеристик (RMS). Эти знания (разделы 7.1–7.3 курса ТОЭ) являются фундаментом для изучения трансформаторов, электрических машин и сложных энергосистем.

Нормативная база

Материал подготовлен с учетом требований следующих стандартов:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». (Определения переменного, синусоидального тока и действующих значений).
ГОСТ 29322-2014 «Напряжения стандартные». (Устанавливает частоту 50 Гц и номиналы напряжений).
ГОСТ 1494-77 «Электротехника. Буквенные обозначения основных величин».

Список рекомендуемой литературы:

Бессонов Л.А. «Теоретические основы электротехники. Электрические цепи» — «Библия» для студентов электротехнических специальностей.
Нейман Л.Р., Демирчян К.С. «Теоретические основы электротехники». Том 1.
Атабеков Г.И. «Основы теории цепей».