Компенсация реактивной мощности: теория, расчет и схемы

Содержание страницы

1. Физическая сущность и значение коэффициента мощности
2. Принципы компенсации реактивной мощности
3. Методика расчета компенсирующих устройств
4. Схемы компенсации и измерения
5. Метод трех вольтметров
6. Пример практического расчета (Задача)
7. Сравнение видов компенсации реактивной мощности
8. Преимущества и недостатки компенсации
9. Интересные факты о реактивной мощности
10. FAQ: Часто задаваемые вопросы

Что такое компенсация реактивной мощности? Это технологический процесс, направленный на снижение потребления реактивной энергии из внешней сети путем генерации её непосредственно у потребителя. Это позволяет разгрузить линии электропередач и трансформаторы, увеличить их срок службы и снизить расходы на электроэнергию.

Краткая история: Проблема возникла с широким внедрением переменного тока в конце XIX века («Война токов»). С появлением асинхронных двигателей промышленные сети столкнулись с фазовым сдвигом тока и напряжения. Первые методы коррекции включали использование синхронных компенсаторов (перевозбужденных двигателей) в начале XX века. Позже, с развитием химии диэлектриков в 1930-х годах, широкое распространение получили статические конденсаторные батареи, которые остаются основным средством компенсации и сегодня.

1. Физическая сущность и значение коэффициента мощности

В теории электрических цепей переменного тока доказано, что активная мощность в цепи (как разветвленной, так и неразветвленной), содержащей реактивные элементы $L$ (индуктивность) и $C$ (емкость), определяется формулой:

P = UI \cos \phi

Где $U$ и $I$ — действующие значения напряжения и тока на входе цепи, а $\cos \phi$ — коэффициент мощности. Это означает, что при неизменных значениях тока и напряжения на зажимах двухполюсника, потребляемая им полезная (активная) мощность может варьироваться от нуля до $UI$ исключительно в зависимости от коэффициента мощности.

Этот факт имеет фундаментальное значение для всей энергетики: от генерации и передачи до распределения и потребления. Рассмотрим предельный случай: если $\cos \phi = 0$, то при наличии напряжения $U$ и протекании тока $I$ активная мощность в нагрузке будет равна нулю. При этом вся энергия, циркулирующая между источником (электростанцией) и потребителем (заводом), будет бесполезно расходоваться на нагрев соединительных проводов.

Важно: Режим $\cos \phi = 0$ на практике является аварийным и недопустимым. Все потребители экономически мотивированы поддерживать $\cos \phi$ близким к единице, используя для этого специальные технические средства компенсации.

2. Принципы компенсации реактивной мощности

В наиболее распространенных случаях компенсация реактивной мощности (стремление свести угол сдвига фаз $\phi$ к нулю) достигается путем параллельного подключения к нагрузке реактивного элемента с характером сопротивления, обратным характеру самой нагрузки:

К активно-индуктивной нагрузке (электродвигатели, трансформаторы) подключают емкостные элементы (конденсаторы).
К активно-емкостной нагрузке (длинные кабельные линии, некоторые специальные установки) подключают индуктивные элементы (реакторы, катушки).

Статистика показывает, что подавляющее большинство промышленных предприятий со станочным парком имеют активно-индуктивный характер нагрузки. Производства с активно-емкостным характером, такие как некоторые электролизные цеха, встречаются значительно реже.

Автоматизация процесса

Современные компенсирующие установки (УКРМ) оснащены контроллерами, которые в реальном времени измеряют реактивную составляющую тока и коммутируют ступени конденсаторных батарей. Это обеспечивает максимальное приближение коэффициента мощности к единице. Однако из-за дискретности номиналов конденсаторов идеальная компенсация («тютелька в тютельку») не всегда возможна, поэтому система работает в режиме небольшой недокомпенсации или перекомпенсации.

3. Методика расчета компенсирующих устройств

Для расчета необходимой емкости или индуктивности выполняют измерения активной мощности $P$, тока нагрузки $I_н$ и напряжения $U$ на известной частоте сети $f$. Если частота неизвестна, её также замеряют.

Алгоритм расчета:

1. Вычисляем текущий коэффициент мощности: $ \cos \phi = \frac{P}{UI_н} $.
2. Определяем реактивную составляющую тока: $ I_р = I_н \sin \phi $ (или через $ I_р = I_н \sqrt{1 — \cos^2 \phi} $).
3. Находим требуемое реактивное сопротивление компенсатора: $ X = \frac{U}{I_р} $.

Далее, в зависимости от характера нагрузки, находим параметры элемента:

Для активно-индуктивной нагрузки (конденсатор): $$ C = \frac{1}{\omega X} = \frac{1}{2\pi f X} $$Для активно-емкостной нагрузки (катушка): $$ L = \frac{X}{\omega} = \frac{X}{2\pi f} $$

Определение характера нагрузки экспериментальным путем

Если характер нагрузки неизвестен заранее, его можно выявить методом пробного подключения. Параллельно нагрузке подключают конденсатор малой емкости (в 2–3 раза меньше расчетной).

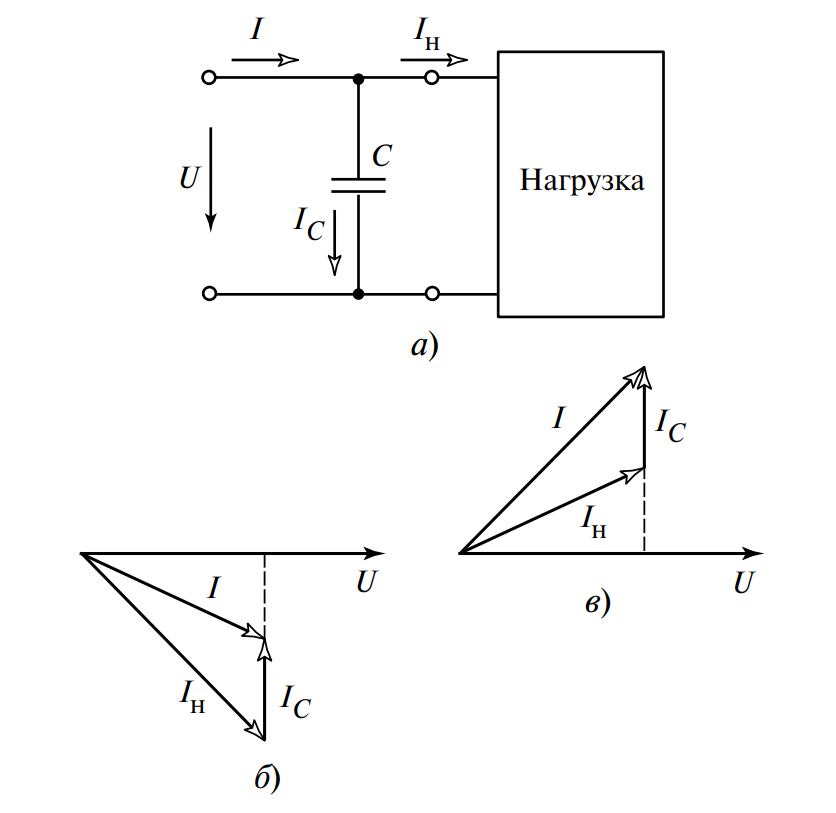
Рис. 1. Схема для определения характера нагрузки (а) и ее векторные диаграммы при индуктивном (б) и емкостном (в) характерах нагрузки

Анализ результатов (см. Рис. 1):

Если общий ток в цепи уменьшился, нагрузка имеет активно-индуктивный характер.
Если общий ток увеличился, нагрузка является активно-емкостной.

Векторные диаграммы (б и в) на рисунке наглядно поясняют сложение токов в обоих случаях.

4. Схемы компенсации и измерения

На Рис. 2 представлена классическая схема компенсации для наиболее распространенной активно-индуктивной нагрузки и векторная диаграмма, иллюстрирующая случай идеальной компенсации (когда ток и напряжение совпадают по фазе).

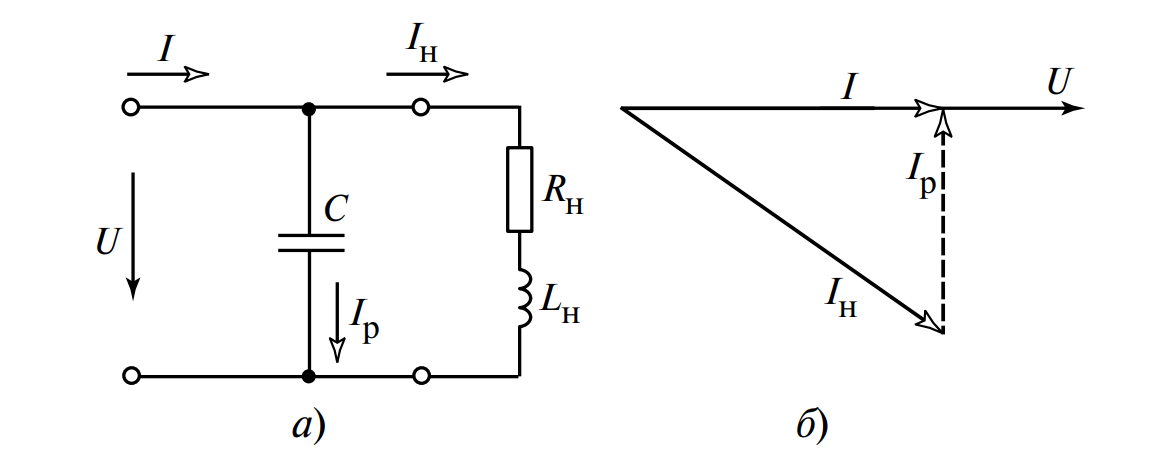
Рис. 2. Схема компенсации реактивной мощности в активно-индуктивной нагрузке (а) и ее векторная диаграмма (б)

Использование фазометра

При отсутствии ваттметра коэффициент мощности определяют путем прямого измерения угла сдвига фаз $\phi$ с помощью фазометра.

Рис. 3. Схема измерения коэффициента мощности

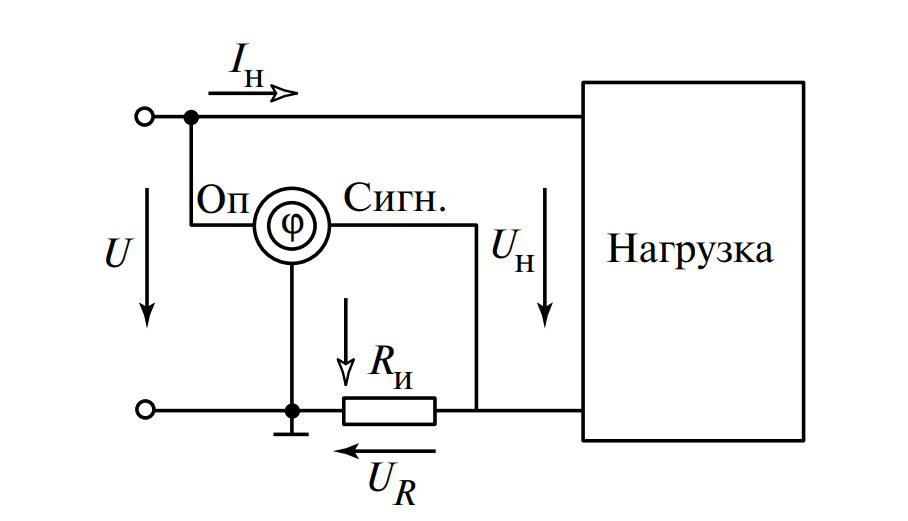
Фазометр имеет два входа:

1. Опорный (Оп): подается напряжение сети.
2. Сигнальный (Сигн.): подается напряжение, пропорциональное току, снимаемое с измерительного резистора $R_и$ ($U_{сигн} = R_и I$).

Для минимизации погрешности сопротивление шунта $R_и$ должно быть значительно меньше сопротивления нагрузки: $ R_и \ll U/I $. В этом случае можно считать $ U_н \approx U $.

Измерив напряжение $U_R$ на резисторе вольтметром, можно найти ток нагрузки $ I_н = U_R / R_и $ без использования амперметра. Зная угол $\phi$ и ток $I_н$, расчет параметров $L$ и $C$ выполняется по методике, описанной выше. Кроме того, данная схема позволяет вычислить параметры нагрузки:

Z_э = \frac{U}{I}, \quad R_э = Z_э \cos \phi, \quad X_э = Z_э \sin \phi

5. Метод трех вольтметров

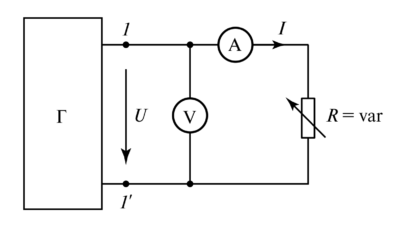
Если в распоряжении инженера имеется только вольтметр, параметры цепи можно определить методом трех вольтметров (схема на Рис. 4, а).

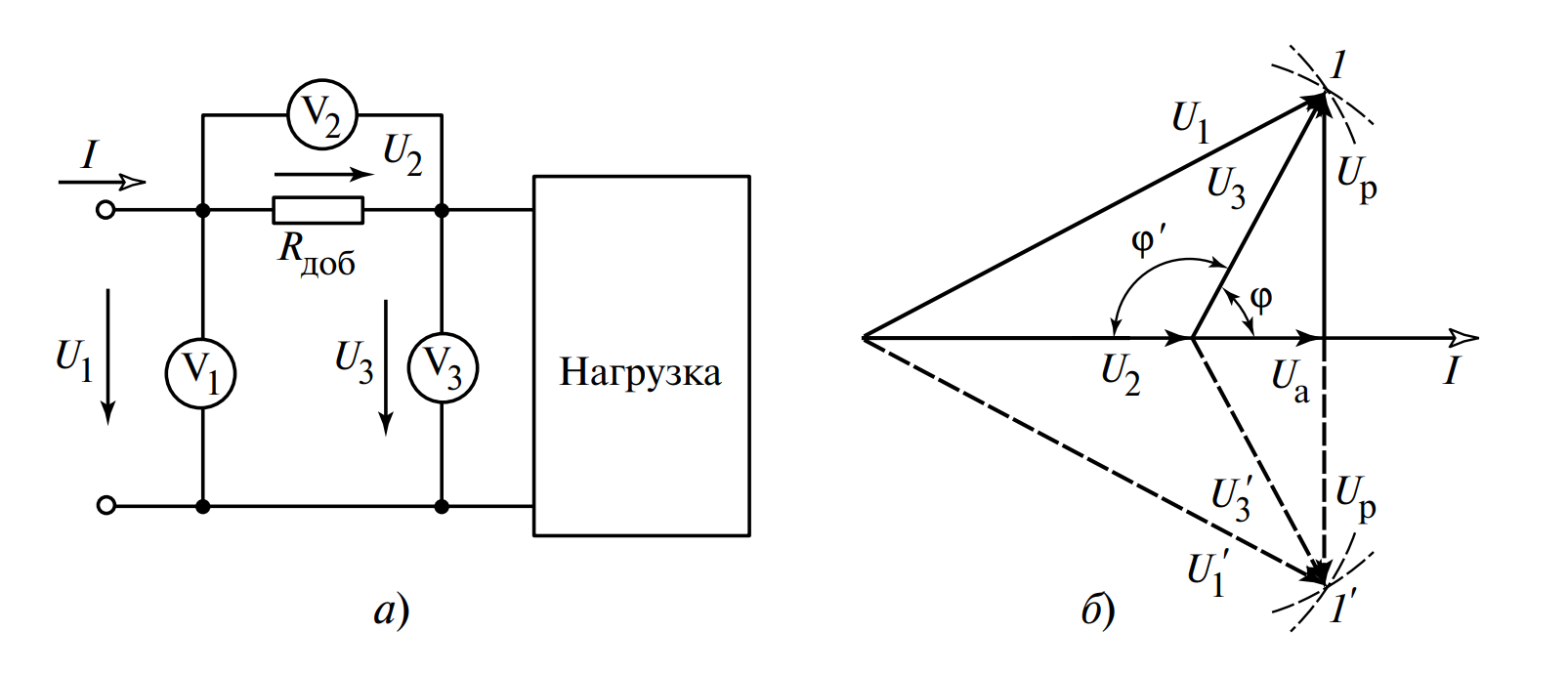
Рис. 4. Измерение сопротивления нагрузки методом трех вольтметров: а — схема измерения; б — векторная диаграмма

Алгоритм метода:

1. Последовательно с нагрузкой включают добавочный резистор с известным сопротивлением $ R_{доб} \approx U/I $.
2. Измеряют три напряжения: общее ($U_1$), на нагрузке ($U_3$) и на резисторе ($U_2$).
3. Так как векторно $\bar{U}_1 = \bar{U}_2 + \bar{U}_3$, строится треугольник напряжений.
4. Вектор $U_2$ совпадает по фазе с током. Из его концов делают засечки радиусами $U_1$ и $U_3$.
5. Точка пересечения дает вершину треугольника. Возможны два решения (симметричные точки 1 и 1′), но характер нагрузки (индуктивный или емкостной) определяется заранее тестом с конденсатором $C’$ (как на Рис. 2).

Расчетные формулы:

Из теоремы косинусов для треугольника напряжений:

U_1^2 = U_2^2 + U_3^2 + 2U_2 U_3 \cos \phi’ $$ $$ \cos \phi’ = \frac{U_1^2 — U_2^2 — U_3^2}{2U_2 U_3}

Угол сдвига фаз нагрузки: $ \phi = 180^\circ — \phi’ $.

Далее рассчитываются параметры:

Активная составляющая напряжения: $ U_а = U_3 \cos \phi $
Реактивная составляющая напряжения: $ U_р = U_3 \sin \phi $
Ток в цепи: $ I = U_2 / R_{доб} $
Полное сопротивление: $ Z_э = U_3 / I $
Активное сопротивление: $ R_э = Z_э \cos \phi $
Реактивное сопротивление: $ X_э = Z_э \sin \phi $

6. Пример практического расчета (Задача)

Условие: Неидеальная катушка подключается сначала к источнику постоянного напряжения 100 В, а затем к источнику синусоидального напряжения частотой 50 Гц с действующим значением 100 В. В первом случае ток равен 5 А, во втором — 4 А.
Требуется: Определить индуктивное сопротивление и индуктивность катушки. Активное сопротивление катушки считать равным её сопротивлению постоянному току. Рассчитать емкость компенсирующего конденсатора $C$.

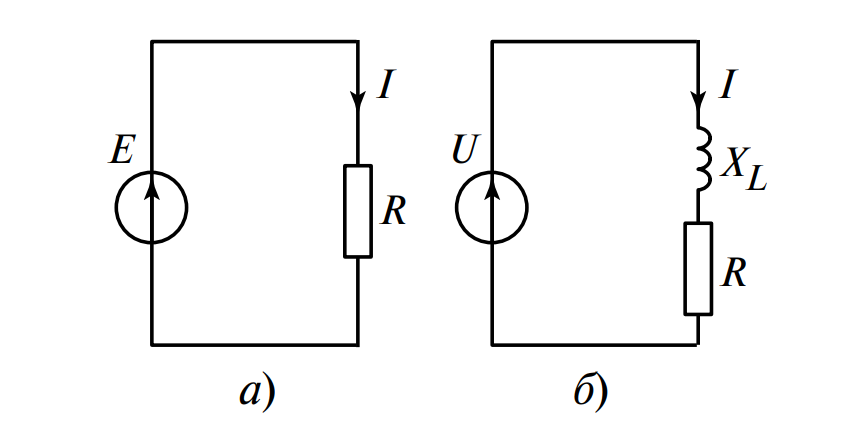
Рис. 5. Эквивалентные схемы для примера 9.5: а — на постоянном токе; б — на переменном токе

Решение:

1. Режим постоянного тока (Рис. 5, а): Частота $f=0$, индуктивное сопротивление $X_L=0$.
Сопротивление цепи чисто активное:
$$ R = \frac{U_{DC}}{I_{DC}} = \frac{100}{5} = 20 \text{ Ом}. $$

2. Режим переменного тока (Рис. 5, б): Частота $f=50$ Гц, угловая частота $\omega = 2\pi f \approx 314$ рад/с.
Полное сопротивление цепи:
$$ Z = \frac{U_{AC}}{I_{AC}} = \frac{100}{4} = 25 \text{ Ом}. $$

3. Определение параметров катушки:
Индуктивное сопротивление находится из треугольника сопротивлений ($Z^2 = R^2 + X_L^2$):
$$ X_L = \sqrt{Z^2 — R^2} = \sqrt{25^2 — 20^2} = \sqrt{625 — 400} = \sqrt{225} = 15 \text{ Ом}. $$
Индуктивность катушки:
$$ L = \frac{X_L}{\omega} = \frac{15}{314} \approx 0,0478 \text{ Гн} = 47,8 \text{ мГн}. $$

4. Расчет компенсации:
Определяем коэффициент мощности катушки:
$$ \cos \phi = \frac{R}{Z} = \frac{20}{25} = 0,8; \quad \sin \phi = \sqrt{1 — 0,8^2} = 0,6. $$
Ток компенсирующего конденсатора (для полной компенсации реактивной составляющей тока катушки):
$$ I_C = I_{AC} \sin \phi = 4 \cdot 0,6 = 2,4 \text{ А}. $$
Необходимая проводимость конденсатора:
$$ B_C = \omega C = \frac{I_C}{U} = \frac{2,4}{100} = 0,024 \text{ См}. $$
Требуемая емкость:
$$ C = \frac{0,024}{314} \approx 76,4 \cdot 10^{-6} \text{ Ф} = 76,4 \text{ мкФ}. $$

7. Сравнение видов компенсации реактивной мощности

Существует три основных способа размещения компенсирующих устройств. Сравним их в таблице:

Вид компенсации	Описание	Преимущества	Недостатки
Индивидуальная	Конденсатор подключается непосредственно к клеммам конкретного потребителя (двигателя).	Разгружает всю питающую сеть от самого потребителя. Нет затрат на коммутационную аппаратуру (включается вместе с нагрузкой).	Высокая стоимость при большом количестве двигателей. Неэффективное использование емкости при простое оборудования.
Групповая	Одна батарея на группу потребителей (например, на распределительном пункте цеха).	Оптимальное соотношение цена/эффективность. Учитывает коэффициент одновременности работы оборудования.	Не разгружает питающие линии от РП до конкретных потребителей.
Централизованная	Установка крупной конденсаторной установки на вводе высокого или низкого напряжения предприятия (ГРЩ).	Простота обслуживания, автоматическое регулирование, минимальная удельная стоимость за кВАр.	Внутренние сети предприятия не разгружаются от реактивных токов, снижаются только платежи внешнему поставщику.

8. Преимущества и недостатки компенсации

Преимущества поддержания высокого $\cos \phi$:

Снижение потерь активной мощности в проводах и трансформаторах ($I^2 R$).
Возможность подключения дополнительной активной нагрузки без замены трансформатора.
Уменьшение падения напряжения в линиях (стабилизация напряжения).
Снижение затрат на электроэнергию (отсутствие штрафов за реактив).
Уменьшение сечения кабелей при проектировании новых сетей.

Недостатки и риски:

Риск перенапряжения при малой нагрузке (если компенсация нерегулируемая).
Возможность возникновения резонансных явлений на гармониках тока.
Затраты на закупку и обслуживание оборудования.

9. Интересные факты о реактивной мощности

Пивная аналогия. Инженеры часто объясняют реактивную мощность на примере пива. Жидкость — это активная мощность (то, что мы пьем), а пена — реактивная (занимает объем в стакане, но не утоляет жажду). Нам приходится платить за «полный стакан» (полная мощность кВА), даже если там много пены.
Синхронные компенсаторы. В середине XX века на заводах часто ставили огромные синхронные двигатели не только для привода, но и для выработки реактивной мощности в сеть (работа в режиме перевозбуждения).
Емкостная нагрузка LED. Массовый переход на LED-освещение и импульсные блоки питания компьютеров создает не индуктивную, а емкостную нагрузку с высоким уровнем гармонических искажений, что требует новых типов фильтрокомпенсирующих устройств.
Энергия магнитного поля. Реактивная энергия не совершает полезной работы, но она необходима для создания электромагнитных полей. Без неё трансформатор не трансформирует, а двигатель просто не будет вращаться.
Эффект Ферранти. На очень длинных линиях электропередач без нагрузки (холостой ход) напряжение в конце линии может стать выше, чем в начале, из-за емкостного эффекта линии (генерации реактивной мощности самой ЛЭП).
Тепловые потери (Закон Джоуля-Ленца). Реактивный ток греет провода точно так же, как и активный. Физике безразлично, «полезный» это ток или нет — нагрев проводника происходит от прохождения любого тока.
Бытовой учет электроэнергии. Обычные бытовые счетчики в квартирах считают только активную энергию. Плата за низкий косинус фи и потери при передаче реактивной энергии ложится на плечи промышленных предприятий, а не частных лиц.

10. FAQ: Часто задаваемые вопросы

1. Почему нельзя просто сделать $\cos \phi = 1$ всегда?
Стремление к идеальной единице чревато «перекомпенсацией». Если нагрузка резко упадет, а конденсаторы не отключатся, сеть станет емкостной. Это может вызвать повышение напряжения (перенапряжение) и неустойчивую работу сети. Обычно целевым значением является 0,95–0,97.

2. В чем разница между кВт и кВА?
кВт (киловатт) — это единица измерения активной (полезной) мощности. кВА (киловольт-ампер) — единица полной мощности, которая включает в себя и активную, и реактивную составляющие. Трансформаторы и генераторы рассчитываются именно в кВА.

3. Поможет ли конденсатор экономить электричество дома?
Для бытового потребителя — практически нет. Бытовые счетчики не учитывают реактивную энергию, а потери в домашней проводке от реактивного тока ничтожно малы по сравнению со стоимостью самого устройства («экономайзеры» из интернета часто являются обманом).

4. Что такое «ступень регулирования»?
В автоматических установках конденсаторы разбиты на группы (ступени), например, 5+10+20 кВАр. Контроллер включает комбинацию этих ступеней, чтобы набрать нужную емкость, как гирьки на весах.

5. Опасны ли конденсаторные установки?
Основная опасность — остаточный заряд. После отключения питания конденсатор может долго сохранять смертельно опасное напряжение. Поэтому они обязательно снабжаются разрядными резисторами, но проверка отсутствия напряжения перед работой обязательна.

Заключение

Компенсация реактивной мощности — это не просто теоретическая задача из учебника, а критически важный элемент эффективности современной энергосистемы. Правильный расчет и выбор оборудования позволяют существенно снизить финансовые издержки предприятия, продлить срок службы дорогостоящих трансформаторов и кабельных линий, а также повысить надежность электроснабжения в целом.

Нормативная база

Для грамотного проектирования и эксплуатации систем компенсации следует руководствоваться действующими стандартами:

ГОСТ 32144-2013 — Нормы качества электрической энергии в системах электроснабжения общего назначения.
ГОСТ IEC 61921-2013 — Конденсаторы силовые. Конденсаторные батареи для коррекции коэффициента мощности низковольтные.
ПУЭ (7-е издание) — Правила устройства электроустановок (Раздел 1.2. Электроснабжение и электрические сети).
Приказ Минэнерго РФ № 380 — О порядке расчета значений соотношения потребления активной и реактивной мощности.

Список рекомендуемой литературы:

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи.
Железко Ю.С. Компенсация реактивной мощности и повышение качества электроэнергии.