Электромагнитная индукция: Физические основы, расчет и анализ

Содержание страницы

1. Физика процесса в движущемся проводнике
2. ЭДС индукции в замкнутом контуре и закон Ленца
3. Явление самоиндукции и понятие индуктивности
4. Практические примеры расчетов
5. Взаимная индукция и коэффициент связи
6. Сравнительный анализ видов индукции
7. Преимущества и недостатки явлений индукции
8. Интересные факты об электромагнитной индукции
9. Часто задаваемые вопросы (FAQ)
Заключение

Явление электромагнитной индукции представляет собой фундаментальный физический процесс возникновения электрического тока, электрического поля или электрической поляризации в проводящем контуре при изменении во времени магнитного потока, пронизывающего данный контур. По сути, это механизм преобразования магнитной энергии (или механической энергии движения в магнитном поле) в электрическую энергию.

Исторически данное открытие стало поворотным моментом в развитии человеческой цивилизации, положив начало эре электротехники. Явление было открыто 29 августа 1831 года выдающимся английским физиком-экспериментатором Майклом Фарадеем. В ходе своих опытов он установил, что генерирование тока возможно только при изменении магнитного состояния системы. Позже математическое обоснование и направление индукционного тока были сформулированы Эмилием Христиановичем Ленцем и Джеймсом Клерком Максвеллом.

Примечание: Электромагнитная индукция лежит в основе работы практически всех современных генераторов электростанций, трансформаторов, электродвигателей и индукционных нагревателей. Без этого явления масштабное производство и передача электроэнергии были бы невозможны.

1. Физика процесса в движущемся проводнике

Для глубокого понимания природы возникновения электродвижущей силы (ЭДС) рассмотрим микроскопические процессы внутри проводника. Представим прямолинейный проводник длиной $ l $, который перемещается с постоянной скоростью $ v $ во внешнем магнитном поле (см. Рисунок 1).

Рисунок 1. Электродвижущая сила индукции в одиночном проводнике

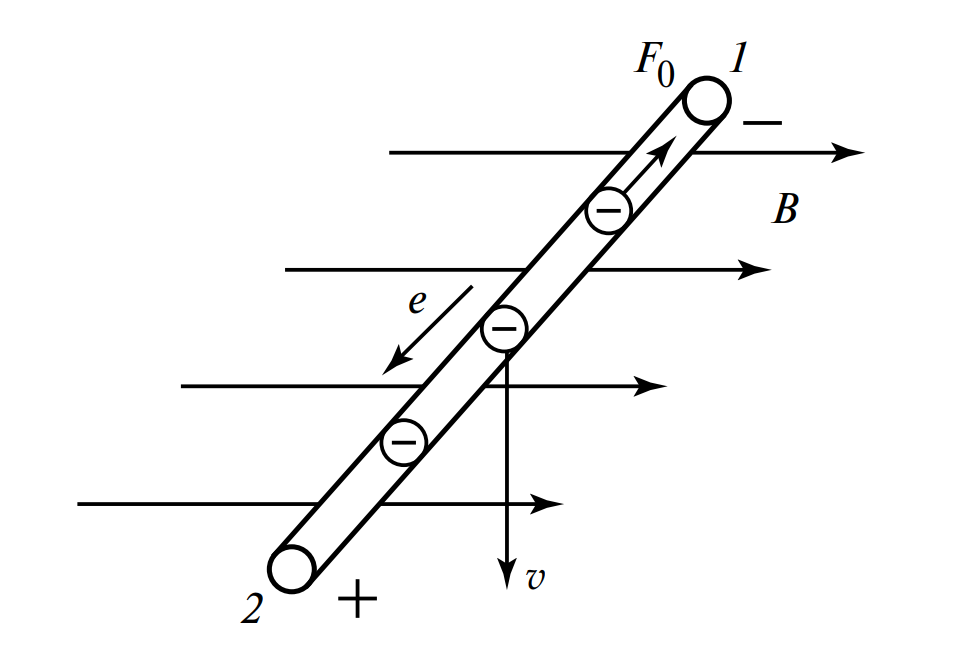
Любой металлический проводник содержит кристаллическую решетку и газ свободных электронов (носителей отрицательного заряда). При механическом перемещении проводника эти носители заряда также движутся в пространстве вместе с телом проводника. Согласно законам электродинамики, на заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца $ F_0 $.

Магнитное поле воздействует на свободные электроны с силой $ F_0 $, вектор которой перпендикулярен как вектору скорости $ v $, так и вектору магнитной индукции $ B $. Под действием этой силы происходит перераспределение зарядов:

Свободные электроны смещаются к одному из краев проводника, обозначим его как край 1. Здесь формируется избыточный отрицательный потенциал.
На противоположном конце, крае 2, образуется недостаток электронов, что равносильно концентрации нескомпенсированных положительных ионов кристаллической решетки. Здесь формируется положительный потенциал.

Разделение зарядов приводит к возникновению внутри проводника собственного электростатического поля (кулоновского поля разделенных зарядов), которое препятствует дальнейшему разделению. Процесс продолжается до тех пор, пока сила Лоренца не будет уравновешена электрической силой. Разность потенциалов между краем 1 и краем 2 и представляет собой наведенную электродвижущую силу (ЭДС) индукции $ e $.

1.1. Математическая модель для прямолинейного проводника

Если проводник длиной $ l $ движется поступательно в однородном магнитном поле с индукцией $ B $ (см. Рисунок 2), величина возникающей ЭДС определяется векторным произведением. В скалярной форме формула выглядит следующим образом:

$$ e = B \cdot v \cdot l \cdot \sin \alpha $$

Где:

$ B $ — модуль вектора магнитной индукции (Тл);
$ v $ — модуль скорости движения проводника (м/с);
$ l $ — активная длина проводника в магнитном поле (м);
$ \alpha $ — угол между вектором скорости $ v $ и вектором магнитной индукции $ B $.

Рисунок 2. Зависимость направления и величины ЭДС от угла движения

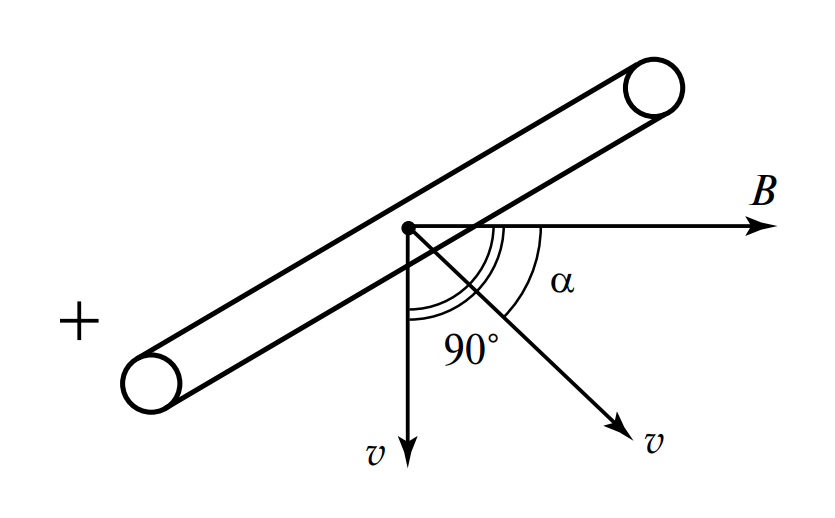
В частном, наиболее эффективном случае, когда скорость $ v $ перпендикулярна вектору индукции $ B $, угол $ \alpha = 90^\circ $, а $ \sin 90^\circ = 1 $. Тогда формула упрощается до:

$$ e = Bvl $$

1.2. Определение полярности ЭДС (Правило правой руки)

Для практического определения направления индукционного тока и полярности ЭДС используется мнемоническое правило правой руки. Это правило позволяет избежать сложных векторных операций в инженерной практике.

Рисунок 3. Применение правила правой руки для определения направления ЭДС

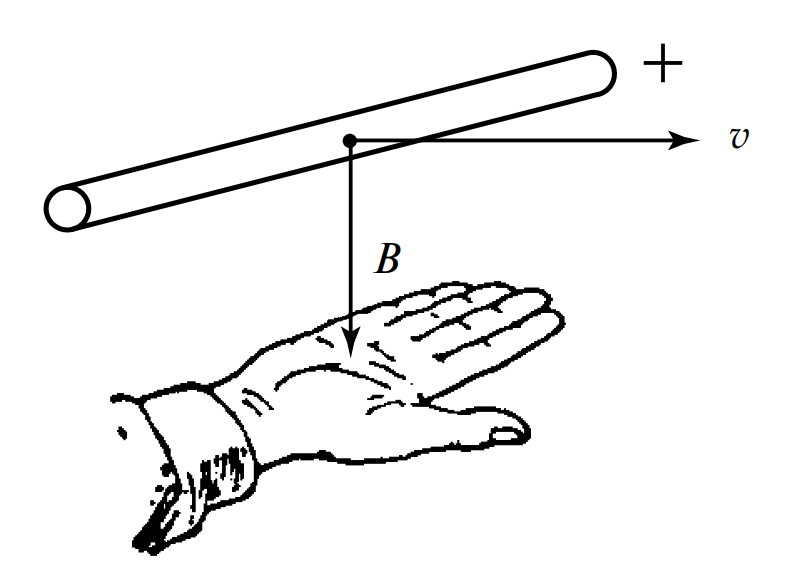
Алгоритм применения правила (согласно Рисунку 3):

Расположите ладонь правой руки так, чтобы магнитные силовые линии $ B $ (идущие от северного полюса N к южному S) входили перпендикулярно в открытую ладонь.
Отогните большой палец на 90 градусов и направьте его по вектору скорости движения проводника $ v $.
Тогда четыре вытянутых сомкнутых пальца укажут направление индукционной ЭДС $ e $ (от «минуса» к «плюсу» внутри источника, то есть направление движения положительных зарядов).

Закон электромагнитной индукции в общей формулировке гласит: любое изменение магнитного поля, в которое помещен проводник произвольной формы, неизбежно вызывает в этом проводнике появление ЭДС электромагнитной индукции.

2. ЭДС индукции в замкнутом контуре и закон Ленца

Перейдем от одиночного проводника к замкнутой системе. Поместим в магнитное поле жесткую проводящую рамку (контур), которая перемещается со скоростью $ v $ перпендикулярно линиям магнитной индукции $ B $ (см. Рисунок 4).

Рисунок 4. Анализ возникновения ЭДС в сторонах рамки

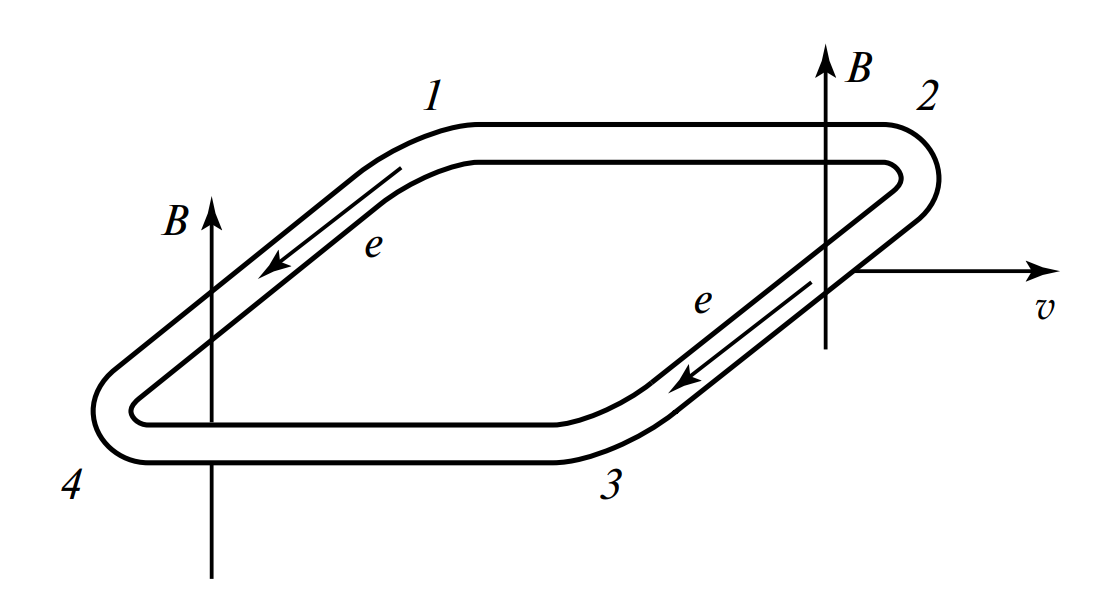
Рассмотрим силы, действующие на стороны рамки:

Стороны 1—4 и 2—3: Эти участки пересекают магнитные силовые линии. В них, согласно описанному выше механизму, индуцируются электродвижущие силы $ e $. Если поле однородно, то эти ЭДС равны по величине и направлены встречно друг другу при обходе контура.
Стороны 1—2 и 3—4: Эти участки движутся вдоль своих осей или так, что не пересекают силовые линии (скользят вдоль них). В них ЭДС не возникает (или равна нулю).

В однородном магнитном поле (где $ B = \text{const} $ во всех точках) суммарная ЭДС в замкнутом контуре будет равна нулю, так как ЭДС в сторонах 1—4 и 2—3 компенсируют друг друга. Ток в рамке протекать не будет.

2.1. Условия возникновения тока и магнитный поток

Индукционный ток возникает только тогда, когда суммарная ЭДС не равна нулю. Это происходит при движении рамки в неоднородном магнитном поле, либо при вращении рамки. Универсальным способом расчета является использование понятия магнитного потока $ \Phi $.

Закон Фарадея-Максвелла для контура гласит:

$$ e = -\frac{\Delta \Phi}{\Delta t} $$

Или в дифференциальной форме:

$$ e = -\frac{d\Phi}{dt} $$

Где $ \Delta \Phi $ — изменение магнитного потока, пронизывающего площадь, ограниченную контуром, за время $ \Delta t $. Магнитный поток $ \Phi $ измеряется в Веберах (Вб) и определяется как $ \Phi = B \cdot S \cdot \cos \beta $, где $ S $ — площадь контура, а $ \beta $ — угол между нормалью к рамке и вектором индукции.

Изменение магнитного потока может быть вызвано тремя основными причинами:

Перемещение рамки в пространстве, где магнитное поле меняется от точки к точке (неоднородность поля).
Изменение самой индукции магнитного поля во времени $ \Phi = f(t) $ (например, переменное поле электромагнита), даже если рамка неподвижна.
Деформация рамки (изменение её площади $ S $ или угла ориентации) в постоянном поле.

2.2. Физический смысл Закона Ленца

Знак «минус» в формуле $ e = -\frac{\Delta \Phi}{\Delta t} $ имеет глубокий физический смысл и является математическим выражением правила Ленца. Оно определяет направление индукционного тока и отражает закон сохранения энергии.

Формулировка закона Ленца: Индукционный ток в замкнутом контуре всегда имеет такое направление, что создаваемый им собственный магнитный поток препятствует тому изменению внешнего магнитного потока, которое вызвало этот ток.

Это своего рода «электромагнитная инерция»:

Если внешний поток сквозь рамку увеличивается ($ \Delta \Phi > 0 $), индуцированный ток создает поле, направленное навстречу внешнему полю, стремясь ослабить его.
Если внешний поток уменьшается ($ \Delta \Phi < 0 $), индуцированный ток создает поле, совпадающее по направлению с внешним, стремясь поддержать его убывание.

3. Явление самоиндукции и понятие индуктивности

Особым случаем электромагнитной индукции является самоиндукция. Она возникает в проводящем контуре (чаще всего в катушке или соленоиде) при изменении силы тока в нем самом.

Рассмотрим катушку, через которую протекает изменяющийся во времени ток $ i $ (см. Рисунок 5). Ток создает собственное магнитное поле, силовые линии которого пронизывают витки этой же катушки.

Рисунок 5. Магнитное поле катушки с током и природа самоиндукции

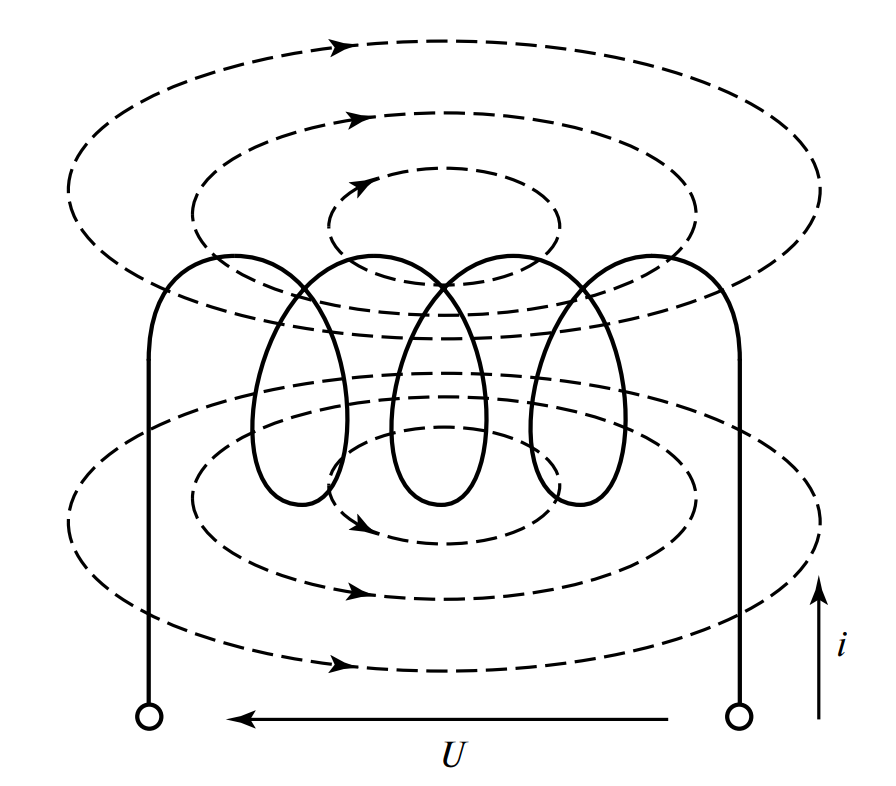
Поскольку ток меняется, меняется и создаваемое им магнитное поле. Следовательно, меняется магнитный поток через витки катушки, что приводит к возникновению ЭДС индукции в самой же катушке. Эту ЭДС называют ЭДС самоиндукции $ e_L $.

3.1. Потокосцепление и индуктивность

Для многовитковой катушки вводится понятие потокосцепления $ \Psi_L $. Это суммарный магнитный поток, сцепленный со всеми витками:

$$ \Psi_L = \Phi_1 + \Phi_2 + \Phi_3 + \dots + \Phi_w $$

Где $ w $ — число витков. В линейной среде (без ферромагнетиков или до насыщения) потокосцепление прямо пропорционально току:

$$ \Psi_L = L \cdot i $$

Коэффициент пропорциональности $ L $ называется индуктивностью катушки. Эта величина зависит от геометрических размеров катушки, числа витков и магнитной проницаемости среды. Единица измерения индуктивности в системе СИ — Генри (Гн).

3.2. Расчет ЭДС самоиндукции

Используя закон электромагнитной индукции для потокосцепления, получаем выражение для ЭДС самоиндукции:

$$ e_L = -\frac{\Delta \Psi_L}{\Delta t} = -L \frac{\Delta i}{\Delta t} $$

В дифференциальной форме (для мгновенных значений):

$$ e_L = -\frac{d\Psi_L}{dt} = -L \frac{di}{dt} \quad (6.1) $$

ЭДС самоиндукции $ e_L $ также подчиняется правилу Ленца: она препятствует изменению тока. Если ток растет, $ e_L $ направлена против тока. Если ток убывает, $ e_L $ поддерживает его (экстратоки размыкания). Именно поэтому мгновенно изменить ток в цепи с индуктивностью невозможно.

4. Практические примеры расчетов

Для закрепления материала рассмотрим решение типовых задач, демонстрирующих применение формул на практике.

Пример 1. Расчет ЭДС во вращающейся рамке

Дано: Квадратная рамка из медного провода сечением $ S_{wire} = 2,5 $ мм². Рамка находится в переменном магнитном поле. Сторона рамки разрезана, к концам подключен вольтметр (см. Рисунок 6, а). Длина стороны рамки $ a = 40 $ см. Длина зазора $ 2 $ мм (пренебрежимо мала). Индукция поля перпендикулярна плоскости рамки и меняется по закону $ B = 1,41 \sin(314t) $.

Рисунок 6. Схемы включения измерительных приборов в контур с переменным магнитным потоком

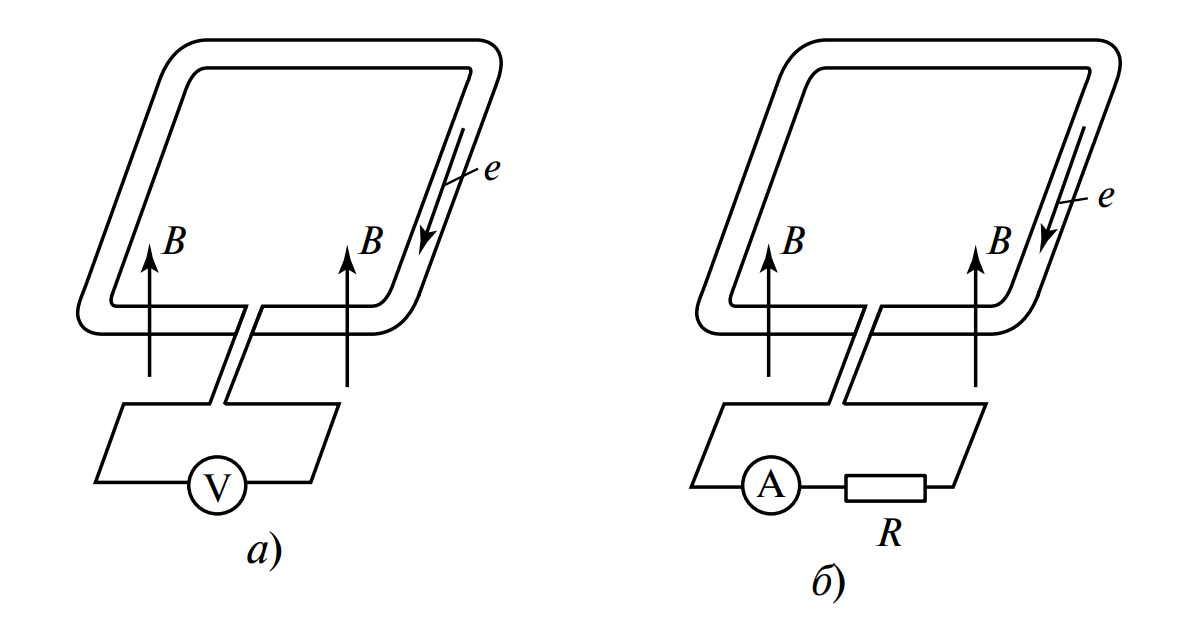
Решение:

1. Определим площадь рамки $ S $:

$$ S = 0,4 \, \text{м} \times 0,4 \, \text{м} = 0,16 \, \text{м}^2 $$

2. Запишем уравнение магнитного потока $ \Phi(t) $:

$$ \Phi = S \cdot B = 0,16 \cdot 1,41 \sin(314t) \approx 0,225 \sin(314t) \, \text{Вб} $$

3. Найдем мгновенное значение ЭДС как производную потока по времени (со знаком минус):

$$ e = -\frac{d\Phi}{dt} = -\frac{d}{dt}(0,225 \sin(314t)) $$
$$ e = -0,225 \cdot 314 \cdot \cos(314t) = -70,8 \cos(314t) \, \text{В} $$

4. Вольтметр электромагнитной системы показывает действующее (эффективное) значение напряжения. Для синусоидального сигнала оно равно амплитуде, деленной на $ \sqrt{2} $:

$$ U = \frac{|E_{max}|}{\sqrt{2}} = \frac{70,8}{1,41} \approx 50,2 \, \text{В} $$

Ответ: Показание вольтметра 50,2 В.

Пример 2. Расчет тока в контуре

Дано: К рамке из примера 6.1 вместо вольтметра подключен резистор $ R = 100 $ Ом и амперметр (см. Рисунок 6, б).

Решение:

1. Необходимо учесть собственное сопротивление медной рамки $ R_{\text{рамки}} $. Длина провода $ l = 4 \times 0,4 = 1,6 $ м. Удельное сопротивление меди $ \rho = 0,0175 $ (в задаче принято 0,018) Ом·мм²/м.

$$ R_m = \frac{\rho l}{S_{wire}} = \frac{0,018 \cdot 1,6}{2,5} \approx 0,011 \, \text{Ом} $$

2. Полное сопротивление цепи равно сумме сопротивления резистора и провода: $ R_{\text{общ}} = 100 + 0,011 \approx 100 $ Ом. (Сопротивлением рамки можно пренебречь ввиду его малости).

3. Мгновенное значение тока по закону Ома:

$$ i = \frac{e}{R} = \frac{-70,8 \cos(314t)}{100} = -0,708 \cos(314t) \, \text{А} $$

4. Показание амперметра (действующее значение):

$$ I = \frac{0,708}{\sqrt{2}} \approx 0,502 \, \text{А} $$

Ответ: Показание амперметра 0,502 А.

5. Взаимная индукция и коэффициент связи

Если две катушки расположены близко друг к другу, магнитное поле одной катушки может пронизывать витки другой. Это явление называется взаимоиндукцией.

Пусть по первой катушке с числом витков $ w_1 $ течет ток $ i_1 $. Он создает:

Поток самоиндукции $ \Phi_{11} $, сцепленный только с первой катушкой.
Поток взаимоиндукции $ \Phi_{12} $, который доходит до второй катушки и пронизывает её витки $ w_2 $.

Аналогично вводятся понятия потокосцеплений:

$$ \Psi_{11} = w_1 \Phi_{11} = L_1 i_1 \quad \text{(самоиндукция)} $$
$$ \Psi_{12} = w_2 \Phi_{12} = M_{12} i_1 \quad \text{(взаимоиндукция)} $$

Коэффициент $ M_{12} $ называется взаимной индуктивностью. В линейных пассивных средах выполняется принцип взаимности: влияние первой катушки на вторую равно влиянию второй на первую, то есть $ M_{12} = M_{21} = M $.

ЭДС, наводимые в катушках при изменении токов, описываются системой уравнений:

$$ e_1 = -L_1 \frac{di_1}{dt} — M \frac{di_2}{dt} $$
$$ e_2 = -L_2 \frac{di_2}{dt} — M \frac{di_1}{dt} $$

(Знаки зависят от направления намотки и токов).

5.1. Коэффициент магнитной связи

Для оценки того, насколько плотно магнитные поля двух катушек связаны друг с другом, используется безразмерный параметр — коэффициент связи $ k $:

$$ k = \frac{M}{\sqrt{L_1 L_2}} $$

Доказательство того, что $ k \le 1 $:

Потокосцепления можно выразить через потоки. Подставляя выражения индуктивностей через потоки в формулу квадрата коэффициента связи, получаем:

$$ k^2 = \frac{M^2}{L_1 L_2} = \frac{\Phi_{12}}{\Phi_{11}} \cdot \frac{\Phi_{21}}{\Phi_{22}} $$

Так как поток взаимоиндукции (часть потока, дошедшая до соседа) всегда меньше или равен полному потоку создающей катушки ($ \Phi_{12} \le \Phi_{11} $ и $ \Phi_{21} \le \Phi_{22} $), то произведение двух дробей, каждая из которых меньше единицы, также меньше единицы.

В силовых трансформаторах с замкнутым железным сердечником $ k \approx 1 $ (жесткая связь).
В воздушных катушках радиоприемников $ k \ll 1 $ (слабая связь).

6. Сравнительный анализ видов индукции

Для удобства систематизации знаний сведем основные типы электромагнитной индукции в таблицу.

Характеристика	ЭДС движения проводника	ЭДС самоиндукции	ЭДС взаимоиндукции
Физическая причина	Сила Лоренца, действующая на заряды в движущемся теле	Изменение собственного магнитного потока при изменении тока	Изменение магнитного потока, созданного соседним контуром
Ключевая формула	$ e = Bvl \sin \alpha $	$ e_L = -L \frac{di}{dt} $	$ e_M = -M \frac{di}{dt} $
Где проявляется	Генераторы, униполярные машины, датчики скорости	Дроссели, катушки фильтров, обмотки двигателей (реактивное сопротивление)	Трансформаторы, беспроводные зарядки, связанные контура
Роль в цепи	Источник энергии (генерация)	Инерционный элемент (сглаживание пульсаций)	Передача энергии или сигнала без гальванического контакта

7. Преимущества и недостатки явлений индукции

Как и любой физический процесс, электромагнитная индукция имеет две стороны медали в технике.

Преимущества (+):

Возможность генерации электрической энергии в промышленных масштабах (ГЭС, АЭС, ТЭЦ).
Возможность трансформации напряжения (повышение/понижение) для передачи энергии на большие расстояния с минимальными потерями.
Бесконтактная передача энергии (индукционные печи, зарядки).
Создание реактивных элементов (индуктивностей) для фильтрации сигналов.

Недостатки (-):

Возникновение паразитных токов Фуко (вихревых токов) в массивных проводниках, что вызывает нагрев и потери энергии (требует шихтования сердечников).
Перенапряжения при коммутации (размыкании) индуктивных цепей, способные пробить изоляцию (опасность ЭДС самоиндукции).
Помехи в линиях связи из-за взаимоиндукции между проводами.

8. Интересные факты об электромагнитной индукции

Закон для необразованных. Майкл Фарадей не имел высшего образования и плохо знал математику. Он описывал явления наглядным языком «силовых линий», над чем поначалу смеялись многие «настоящие» математики того времени, пока Максвелл не перевел идеи Фарадея на язык строгих формул.
Основа релятивизма. Электромагнитная индукция — одно из явлений, которое привело Эйнштейна к созданию Специальной теории относительности. Он заметил, что описание явления зависит от того, что мы считаем движущимся (магнит или проводник), хотя результат (ток) одинаков.
Левитация. Правило Ленца может быть настолько сильным, что способно удерживать тяжелые предметы в воздухе. Это используется в поездах на магнитной подушке (Маглев).
Индукционная плита. В вашей кухне используется этот же закон. Плита создает быстропеременное магнитное поле, которое наводит вихревые токи непосредственно в дне посуды, нагревая её, а сама поверхность плиты остается холодной.
Беспроводное будущее. Технология зарядки смартфонов Qi основана на принципе взаимоиндукции, описанном в данной статье (две катушки: передающая и приемная).
Земля как генератор. В длинных тросах спутников, движущихся по орбите в магнитном поле Земли, наводятся колоссальные напряжения, которые теоретически можно использовать для питания бортовых систем (проект «Tethered Satellite System»).
Сверхпроводимость. В сверхпроводнике ЭДС индукции может вызвать ток, который будет течь вечно, так как сопротивление равно нулю (эффект Мейснера и незатухающие токи).

9. Часто задаваемые вопросы (FAQ)

1. Почему в формуле закона Фарадея стоит знак минус?

Знак минус отражает Закон Ленца. Он указывает на то, что ЭДС индукции порождает ток, магнитное поле которого направлено против изменения внешнего магнитного потока. Это проявление закона сохранения энергии.

2. Что такое вихревые токи и как с ними бороться?

Вихревые токи (токи Фуко) — это индукционные токи, возникающие в массивных кусках металла при изменении магнитного поля. Они вызывают нагрев. Для борьбы с ними сердечники трансформаторов и двигателей делают не сплошными, а набирают из тонких изолированных пластин электротехнической стали.

3. Зависит ли индуктивность катушки от тока в ней?

Для катушки без сердечника (воздушной) — нет, индуктивность постоянна. Для катушки с ферромагнитным сердечником индуктивность зависит от тока, так как магнитная проницаемость материала сердечника меняется в зависимости от напряженности поля (явление насыщения).

4. Можно ли получить постоянный ток с помощью индукции?

Напрямую индукция генерирует переменный ток (так как требуется изменение потока). Чтобы получить постоянный ток (как в генераторах постоянного тока), используют механический выпрямитель (коллектор) или электронные диодные мосты.

5. В чем разница между Генри и Вебером?

Вебер (Вб) — это единица магнитного потока (сколько линий поля пронзает рамку). Генри (Гн) — это характеристика самой катушки (индуктивность), показывающая, какой поток создаст эта катушка при протекании в ней тока в 1 Ампер.

Заключение

Закон электромагнитной индукции является фундаментом современной электротехники и электроники. Рассмотренные в статье принципы генерации ЭДС в движущемся проводнике, законы самоиндукции и взаимоиндукции позволяют инженерам проектировать сложнейшие устройства: от миниатюрных RFID-меток до гигантских турбогенераторов АЭС. Понимание математического аппарата (производные потока, векторные произведения) и физической сути процесса (взаимодействие полей и зарядов) необходимо любому специалисту технического профиля для грамотного анализа и разработки электрических цепей.

Нормативная база

При проектировании и расчетах электромагнитных устройств необходимо руководствоваться действующими государственными стандартами:

IEC 60050-121(1998)/Amd.5(2021), который называется «Международный электротехнический словарь. Часть 121. Электромагнетизм. Изменение 5» — устанавливает современную терминологию.
ГОСТ 8.417-2024 (ГСИ. Единицы величин) — регламентирует использование единиц СИ (Генри, Тесла, Вебер).
ГОСТ Р 52002-2003 (Электротехника. Термины и определения основных понятий) — базовый стандарт для электротехнических определений.

Список литературы

Тамм И. Е. Основы теории электричества. — М.: Физматлит, 2003. — (Классический фундаментальный труд по электродинамике).
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2020. — (Базовый учебник для инженеров-энергетиков и электриков).
Сивухин Д. В. Общий курс физики. Том 3. Электричество. — М.: Физматлит, 2015. — (Углубленный университетский курс общей физики).