Электрическое напряжение и потенциал: определения и связь

Содержание страницы

1. Определение электрического напряжения
2. Потенциальные и вихревые поля (ЭДС)
3. Электрический потенциал
4. Сравнение напряжения и потенциала
5. Интересные факты о напряжении и потенциале
6. Часто задаваемые вопросы (FAQ)
Заключение

Электрическое напряжение — это одно из фундаментальных понятий в физике и электротехнике. Если говорить просто, напряжение — это «давление» в электрической цепи, которое заставляет электрический заряд (ток) двигаться. Без напряжения не будет тока, точно так же, как вода не потечет по трубе, если нет разницы в давлении или высоте.

Исторически концепция напряжения неразрывно связана с работами Алессандро Вольта, который в 1800 году создал «вольтов столб» — первый химический источник тока. Эта «гальваническая батарея» создавала постоянную разность потенциалов (напряжение) между полюсами, что позволило начать систематическое изучение электрического тока. Понятия напряжения и потенциала были формализованы позже, в работах таких ученых, как Ом, Фарадей и Максвелл, заложивших основы классической электродинамики.

В этой статье мы рассмотрим строгое математическое и физическое определение напряжения, его связь с напряженностью электрического поля и введем понятие электрического потенциала.

1. Определение электрического напряжения

В общем случае, под напряжением вдоль определенного пути $1m2$ (из точки 1 в точку 2) понимается физическая величина, которая равна отношению работы $A$, совершаемой силами электрического поля по перемещению заряда $Q$ из точки 1 в точку 2, к величине этого заряда.

Математически это выражается формулой:

$$ u_{12} = \frac{A}{Q} $$

Единицей измерения напряжения в системе СИ является Вольт (В). Как следует из формулы (1), 1 Вольт равен 1 Джоулю на 1 Кулон:

$ 1 \, \text{В} = 1 \, \text{Дж} / \text{Кл} $

Наряду с основной единицей, вольтом, широко используются дольные и кратные единицы: милливольт ($1 \, \text{мВ} = 1 \times 10^{-3} \, \text{В}$) и киловольт ($1 \, \text{кВ} = 1 \times 10^{3} \, \text{В}$).

Примечание: Стандарты на единицы физических величин, включая Вольт, и их правильное применение в Российской Федерации устанавливаются нормативными документами. Основным документом в этой области является ГОСТ 8.417-2024 «Государственная система обеспечения единства измерений (ГСИ). Единицы величин».

1.1. Связь напряжения с напряженностью поля

В электротехнике принято более строгое определение напряжения через фундаментальную характеристику электрического поля — его напряженность $ \mathbf{E} $. Напряженность поля — это векторная величина, показывающая, с какой силой поле действует на единичный положительный заряд.

Рассмотрим путь заряда из точки 1 в точку 2, как показано на рисунке 1. Разобьем этот путь на $N$ очень малых (элементарных) участков $ d\mathbf{l}_i $.

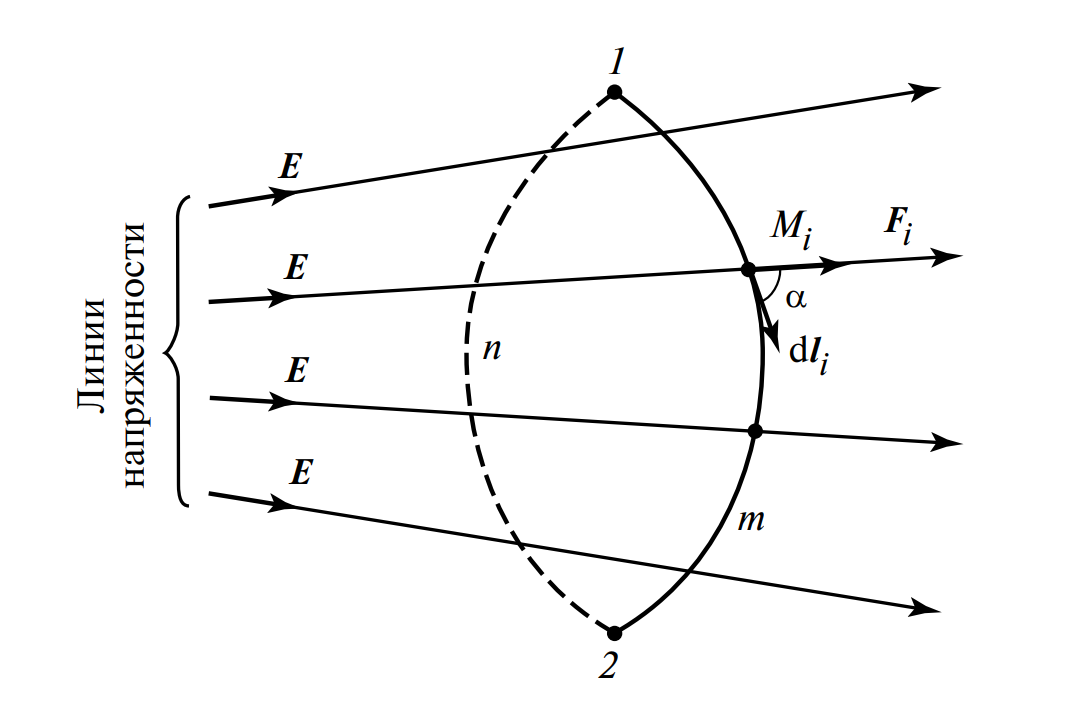
Рисунок 1. Перемещение заряженной частицы в электрическом поле. Вектор $ \mathbf{E} $ показывает направление линий напряженности, $ d\mathbf{l} $ — элементарный участок пути, $ \alpha $ — угол между ними.

Из курса физики известно, что элементарная работа $ dА_i $ сил поля на $i$-м участке равна скалярному произведению вектора силы $ \mathbf{F}_i $, действующей на заряд $Q$, на вектор элементарного пути $ d\mathbf{l}_i $. Сила, в свою очередь, равна $ \mathbf{F}_i = Q\mathbf{E}_i $.

Таким образом, элементарная работа равна:

$$ dА_i = \mathbf{F}_i \cdot d\mathbf{l}_i = Q\mathbf{E}_i \cdot d\mathbf{l}_i = QE_i \cos(\alpha_i) dl_i $$

Здесь $ E_i $ и $ dl_i $ — модули векторов напряженности и элемента пути, а $ \alpha_i $ — угол между ними в точке $ M_i $.

Полная работа $A$ по перемещению заряда из точки 1 в точку 2 находится путем суммирования элементарных работ. Если устремить число участков к бесконечности ($N \to \infty$) а длину каждого из них к нулю ($dl_i \to 0$), сумма переходит в интеграл:

$$ A = \sum_{i=1}^{N} dА_i = Q \sum_{i=1}^{N} \mathbf{E}_i \cdot d\mathbf{l}_i \to A = Q \int_{1}^{2} \mathbf{E} \cdot d\mathbf{l} $$

Подставляя это выражение для работы в формулу (1), получаем окончательное определение напряжения:

$$ u_{12} = \frac{A}{Q} = \frac{Q \int_{1}^{2} \mathbf{E} \cdot d\mathbf{l}}{Q} = \int_{1}^{2} \mathbf{E} \cdot d\mathbf{l} $$

Таким образом, электрическое напряжение — это физическая величина, характеризующая электрическое поле вдоль рассматриваемого пути и равная линейному интегралу вектора напряженности электрического поля вдоль этого пути.

2. Потенциальные и вихревые поля (ЭДС)

Ключевой особенностью определения (3) является то, что в общем случае значение напряжения $ u_{12} $ **зависит от пути интегрирования**.

Вернемся к рисунку 1. Если мы будем перемещать заряд из точки 1 в точку 2 по другому пути, например, по пути $1n2$ (изображен пунктиром), то значение интеграла (3) может измениться. Следовательно, $ u_{1m2} \neq u_{1n2} $.

Если интеграл напряженности по замкнутому контуру (например, $1m2n1$) отличен от нуля, такое поле называется вихревым или непотенциальным. В этом случае:

$$ \oint_{1m2n1} \mathbf{E} \cdot d\mathbf{l} = e \neq 0 $$

Величину $e$ называют электродвижущей силой (ЭДС). Именно ЭДС, создаваемая сторонними (неэлектрическими) силами в источниках питания (батареях, генераторах), является причиной существования вихревых полей и поддержания постоянного тока в цепи.

Однако существует класс полей, в которых работа не зависит от пути. Это потенциальные поля. Для них интеграл по любому замкнутому контуру всегда равен нулю:

$$ \oint \mathbf{E} \cdot d\mathbf{l} = 0 $$

Для потенциальных полей значение напряжения между точками 1 и 2 всегда однозначно и не зависит от выбора пути.

Классическим примером потенциального поля является электростатическое поле, создаваемое неподвижными зарядами. В таком поле напряженность $ \mathbf{E} $ в каждой точке постоянна во времени. Соответственно, и напряжение между двумя любыми точками постоянно. Постоянное напряжение принято обозначать прописной буквой $U$:

$$ U_{12} = \int_{1}^{2} \mathbf{E} \cdot d\mathbf{l} $$

3. Электрический потенциал

В потенциальных электростатических полях напряжение $ U_{12} $ часто называют разностью потенциалов точек 1 и 2 и обозначают как $ \phi_1 — \phi_2 $ (или $ U_1 — U_2 $).

Это позволяет ввести новую физическую величину — электрический потенциал $ \phi_j $.

Электрический потенциал $ \phi_j $ некоторой точки $j$ — это скалярная величина, равная электрическому напряжению (разности потенциалов) $ U_{jp} $ между данной точкой $j$ и другой, произвольно выбранной точкой $p$, называемой точкой нулевого потенциала ($ \phi_p = 0 $).

Потенциал, как и напряжение, измеряется в Вольтах (В).

Из определения следует, что значение потенциала в конкретной точке $j$ зависит от выбора «нулевой» точки $p$. Однако разность потенциалов между двумя любыми точками $j=1$ и $j=2$ от этого выбора не зависит. Убедимся в этом:

$$ U_{12} = \phi_1 — \phi_2 = (\phi_1 — \phi_p) — (\phi_2 — \phi_p) = \phi_1 — \phi_2 $$

Выбор точки нулевого потенциала $p$ диктуется исключительно удобством решения задачи:

В теоретической физике, при рассмотрении бесконечных сред, за точку $p$ часто принимают бесконечно удаленную точку.
В практической электротехнике и электронике за точку нулевого потенциала ($ \phi = 0 $) почти всегда принимают точку, физически соединенную с землей (такая точка называется «заземленной» или «общим проводом»).

3.1. Пример 1. Расчет поля в конденсаторе

Определим напряжение $ U_{12} $ и потенциалы $ \phi_a, \phi_b, \phi_c $ точек в плоском воздушном конденсаторе (рис. 2). Конденсатор состоит из двух параллельных металлических пластин, заряженных разноименно.

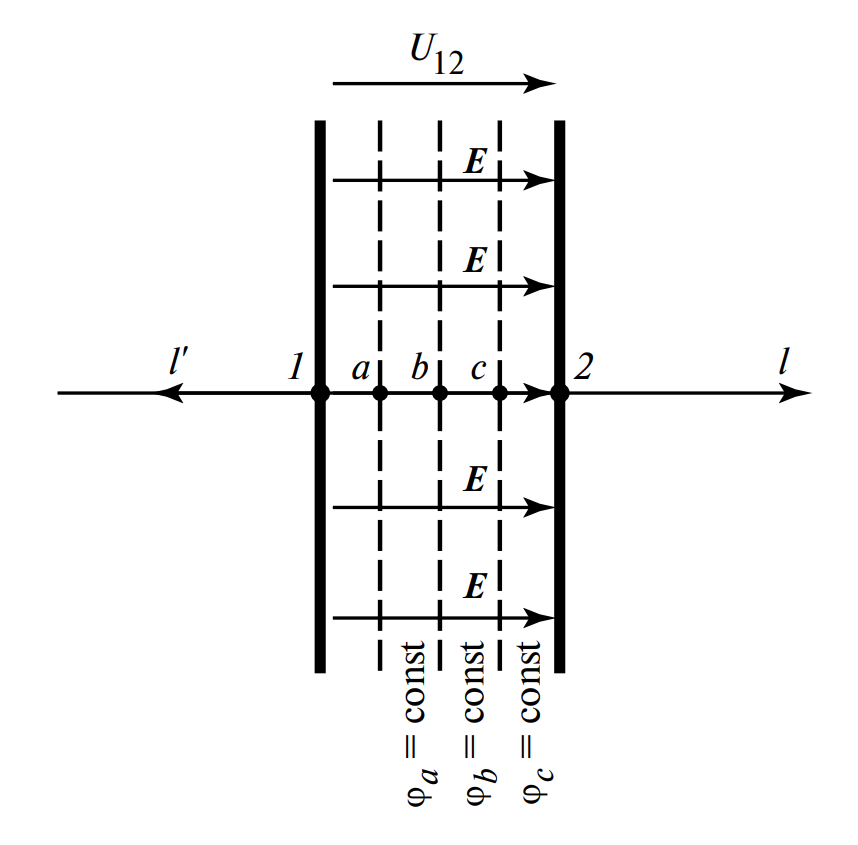
Рисунок 2. Линии напряженности электрического поля (сплошные линии с $ \mathbf{E} $) и эквипотенциали (штриховые линии $ \phi = \text{const} $) в воздушном конденсаторе.

Условия задачи:

Поле между пластинами однородно, его напряженность $ E = 10^4 \, \text{В/м} $.
Расстояние между пластинами $ l = 1 \, \text{см} = 10^{-2} \, \text{м} $.
Точки $a, b, c$ делят расстояние $l$ на четыре равных отрезка.
Точка 2 (нижняя пластина) принята за точку нулевого потенциала, т.е. $ \phi_p = \phi_2 = 0 \, \text{В} $.

Решение:

1. Определение напряжения $ U_{12} $:

Проведем ось $l$ от точки 1 к точке 2. Вектор $ \mathbf{E} $ и элементарный вектор $ d\mathbf{l} $ сонаправлены, поэтому $ \mathbf{E} \cdot d\mathbf{l} = E \, dl $. Напряжение $ U_{12} $ — это разность потенциалов $ \phi_1 — \phi_2 $.

$$ U_{12} = \int_{1}^{2} \mathbf{E} \cdot d\mathbf{l} = \int_{l=0}^{10^{-2}} E \, dl = E \cdot l \Big|_{0}^{10^{-2}} = (10^4 \, \text{В/м}) \cdot (10^{-2} \, \text{м}) = 100 \, \text{В} $$

Поскольку $ \phi_2 = 0 $, то потенциал верхней пластины $ \phi_1 = 100 \, \text{В} $.

2. Определение потенциалов точек $a, b, c$:

Проведем ось $l’$ из точки 2 (нулевой потенциал) вверх. Координаты точек будут: $ l’_a = 2.5 \times 10^{-3} \, \text{м} $, $ l’_b = 5 \times 10^{-3} \, \text{м} $, $ l’_c = 7.5 \times 10^{-3} \, \text{м} $.

Потенциал $ \phi_a $ — это напряжение $ U_{a2} = \phi_a — \phi_2 $. При движении по оси $l’$ от точки 2 к точке $a$, вектор $ d\mathbf{l’} $ направлен вверх, а вектор $ \mathbf{E} $ — вниз. Они противонаправлены, т.е. $ \mathbf{E} \cdot d\mathbf{l’} = E \, dl’ \cos(180^{\circ}) = -E \, dl’ $.

Используем определение разности потенциалов: $ \phi_a — \phi_2 = — \int_{2}^{a} \mathbf{E} \cdot d\mathbf{l’} $

Так как $ \phi_2 = 0 $:

$$ \phi_a = — \int_{l’=0}^{2.5 \times 10^{-3}} (-E) \, dl’ = \int_{0}^{2.5 \times 10^{-3}} E \, dl’ = E \cdot l’ \Big|_{0}^{2.5 \times 10^{-3}} = (10^4) \cdot (2.5 \times 10^{-3}) = 25 \, \text{В} $$

Аналогично для других точек:

$$ \phi_b = \int_{0}^{5 \times 10^{-3}} E \, dl’ = E \cdot l’ \Big|_{0}^{5 \times 10^{-3}} = (10^4) \cdot (5 \times 10^{-3}) = 50 \, \text{В} $$

$$ \phi_c = \int_{0}^{7.5 \times 10^{-3}} E \, dl’ = E \cdot l’ \Big|_{0}^{7.5 \times 10^{-3}} = (10^4) \cdot (7.5 \times 10^{-3}) = 75 \, \text{В} $$

Примечание:

Линии, пересекающие силовые линии (линии напряженности) под прямым углом (90°), называют линиями равного потенциала, или эквипотенциалями. На рис. 2 эквипотенциали $ \phi_a = \text{const} $, $ \phi_b = \text{const} $ и $ \phi_c = \text{const} $ показаны штриховыми линиями. В однородном поле это параллельные прямые.

4. Сравнение напряжения и потенциала

Хотя эти термины часто взаимозаменяемы в быту, в физике и электротехнике они имеют разный, хотя и связанный, смысл.

Характеристика	Электрическое напряжение (Разность потенциалов)	Электрический потенциал
Определение	Работа по перемещению единичного заряда между двумя точками.	Работа по перемещению единичного заряда из данной точки в точку нулевого потенциала.
Обозначение	$ U_{12} $, $ u(t) $, $ \Delta \phi $	$ \phi $, $ V $
Физический смысл	Характеризует поле между двумя точками или вдоль пути. Является причиной движения зарядов (тока).	Характеризует энергетическое состояние одной точки поля (относительно базы).
Зависимость	Абсолютная величина (в потенциальном поле). Не зависит от выбора «нуля».	Относительная величина. Зависит от выбора точки «нулевого» потенциала.
Измерение	Измеряется вольтметром, подключаемым к двум точкам.	Напрямую измерить нельзя. Можно измерить только разность потенциалов (напряжение).

5. Интересные факты о напряжении и потенциале

Птицы на проводах. Птицы спокойно сидят на высоковольтных проводах, потому что обе их лапы находятся на одном проводе, то есть имеют практически одинаковый потенциал ($ \phi_1 \approx \phi_2 $). Разность потенциалов $ U = \phi_1 — \phi_2 \approx 0 $, поэтому ток через птицу не идет. Но если птица коснется крылом другого провода или заземленной опоры — она погибнет.
«Водяная» аналогия. Напряжение часто сравнивают с давлением воды в трубе или с разницей уровней воды в двух сосудах. Чем больше разница (напряжение), тем сильнее поток воды (ток).
Живое электричество. Нервные импульсы в теле человека и животных — это, по сути, волны изменения разности потенциалов (напряжения) на мембранах нервных клеток, вызванные движением ионов.
Почему «земля»? В электротехнике «землю» (корпус прибора, планету Земля) принимают за $ \phi = 0 $. Это удобно, так как Земля — огромный проводник, чей потенциал практически невозможно изменить, добавив или забрав небольшой заряд.
Опасен не вольт, а ампер? Расхожее мнение, что убивает ток (Амперы), а не напряжение (Вольты). Это верно лишь отчасти. Ток действительно оказывает поражающее действие, но этот ток создает именно напряжение (согласно закону Ома, $ I = U/R $). Без достаточного напряжения опасный ток через тело человека (обладающее сопротивлением $R$) просто не потечет.

6. Часто задаваемые вопросы (FAQ)

1. В чем разница между напряжением и ЭДС?

Ответ: Оба измеряются в Вольтах и характеризуют работу по перемещению заряда. Напряжение (или разность потенциалов) — это характеристика потенциального поля (например, поля внутри резистора). ЭДС (Электродвижущая сила) — это характеристика источника (батареи, генератора), она описывает работу сторонних (неэлектрических) сил, которые и создают это напряжение, разделяя заряды.

2. Почему напряжение иногда обозначают $U$ (прописная), а иногда $u$ (строчная)?

Ответ: Это стандартное соглашение в электротехнике. Прописной буквой $U$ обычно обозначают постоянные величины (напряжение в цепи постоянного тока) или действующие (RMS) значения в цепях переменного тока. Строчной буквой $u$ (часто $u(t)$) обозначают мгновенное значение напряжения, которое изменяется во времени.

3. Всегда ли напряжение — это разность потенциалов?

Ответ: Строго говоря, нет. Понятие «потенциал» вводится только для потенциальных полей (например, электростатического). Только в них напряжение $ U_{12} $ однозначно равно разности потенциалов $ \phi_1 — \phi_2 $. В вихревых полях (где $ \oint \mathbf{E} \cdot d\mathbf{l} \neq 0 $), работа зависит от пути, и само понятие потенциала как $ \phi = \int \mathbf{E} \cdot d\mathbf{l} $ теряет однозначность.

4. Можно ли измерить потенциал в точке?

Ответ: Напрямую — нет. Любой измерительный прибор, например, вольтметр, всегда измеряет разность потенциалов между двумя точками (между двумя его щупами). Если вы «измеряете потенциал» в точке, вы на самом деле измеряете напряжение между этой точкой и «общим» проводом (землей) прибора, который принят за $ \phi = 0 $.

5. Что такое «эквипотенциальная поверхность»?

Ответ: Это воображаемая поверхность (или линия, как на рис. 2), во всех точках которой электрический потенциал имеет одинаковое значение. Поскольку разность потенциалов между любыми двумя точками на такой поверхности равна нулю ($ \Delta \phi = 0 $), то и работа по перемещению заряда вдоль этой поверхности равна нулю. Из этого следует, что вектор напряженности поля $ \mathbf{E} $ всегда перпендикулярен эквипотенциальной поверхности.

Заключение

Электрическое напряжение и потенциал являются ключевыми понятиями для описания электрических полей и цепей. Напряжение, определяемое как работа по перемещению заряда или как линейный интеграл напряженности поля, служит движущей силой для электрического тока. Введение понятия потенциала в электростатических полях значительно упрощает расчеты, сводя векторные задачи к скалярным.

Понимание разницы между напряжением, потенциалом и ЭДС, а также между потенциальными и вихревыми полями, является фундаментом для изучения всех разделов электротехники, от теории цепей до электродинамики.

Нормативная база

ГОСТ 8.417-2024 «Государственная система обеспечения единства измерений (ГСИ). Единицы величин». — (Устанавливает определения и обозначения единиц СИ, включая Вольт, Ампер, Кулон, Джоуль).
ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». — (Дает стандартизированные определения для терминов «электрическое поле», «напряженность» и др.).

Список рекомендуемой литературы

Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е изд. — М.: Гардарики, 2007.
Калашников С. Г. Электричество (Курс общей физики, том 2). — 6-е изд. — М.: Физматлит, 2003.
Зевеке Г. В., Ионкин П. А., Нетушил А. В. Основы теории цепей. — М.: Энергоатомиздат, 1989.
Савельев И. В. Курс общей физики. Том 2. Электричество и магнетизм. — М.: Наука, 1988.