Законы Кирхгофа и полная система уравнений электрической цепи

Содержание страницы

1. Первый закон Кирхгофа (Закон токов, KCL)
2. Второй закон Кирхгофа (Закон напряжений, KVL)
3. Компонентные уравнения и полная система
4. Оптимизация: Гибридная форма уравнений
5. Постановка задачи анализа электрической цепи
6. Пример 1: Расчет цепи на Рис. 1
7. Сравнение Первого и Второго законов Кирхгофа
8. Интересные факты о законах Кирхгофа
9. Часто задаваемые вопросы (FAQ)
Заключение

Законы Кирхгофа представляют собой два фундаментальных правила (или принципа), которые лежат в основе теории электрических цепей. Они являются обобщением закона Ома и позволяют рассчитывать сложные разветвленные цепи как постоянного, так и переменного тока. Эти законы описывают сохранение двух ключевых физических величин: электрического заряда (Первый закон) и энергии (Второй закон).

Они были сформулированы немецким физиком Густавом Кирхгофом в 1845 году, когда он был еще студентом. Эти правила позволили перейти от расчета простых последовательных и параллельных соединений к анализу цепей произвольной топологии.

Для исчерпывающего математического описания электромагнитных процессов в любой электрической цепи формируется полная система уравнений. Эта система является совокупностью трех групп уравнений:

Уравнения, составленные на основе Первого закона Кирхгофа (KCL);
Уравнения, составленные на основе Второго закона Кирхгофа (KVL);
Компонентные уравнения, которые описывают физические свойства (вольт-амперные характеристики) каждого отдельного элемента цепи.

1. Первый закон Кирхгофа (Закон токов, KCL)

Формулировка первого закона Кирхгофа (также известного как закон токов Кирхгофа) гласит: алгебраическая сумма токов, сходящихся в любом узле электрической цепи, равна нулю.

Математически это записывается как:
$$ \sum_{k=1}^{n} I_k = 0 $$
Этот закон является прямым следствием закона сохранения электрического заряда: заряд не может накапливаться в узле или исчезать из него.

Для составления уравнений необходимо принять соглашение о знаках. Обычно токи, вытекающие из узла, записываются со знаком «плюс», а токи, втекающие в узел, — со знаком «минус» (или наоборот, главное — придерживаться одного правила).

Для электрической цепи, содержащей $y$ узлов, можно составить ровно $y — 1$ независимое уравнение по первому закону Кирхгофа. Уравнение для последнего, $y$-го узла, всегда будет линейной комбинацией (суммой) остальных $y — 1$ уравнений и, следовательно, не является независимым.

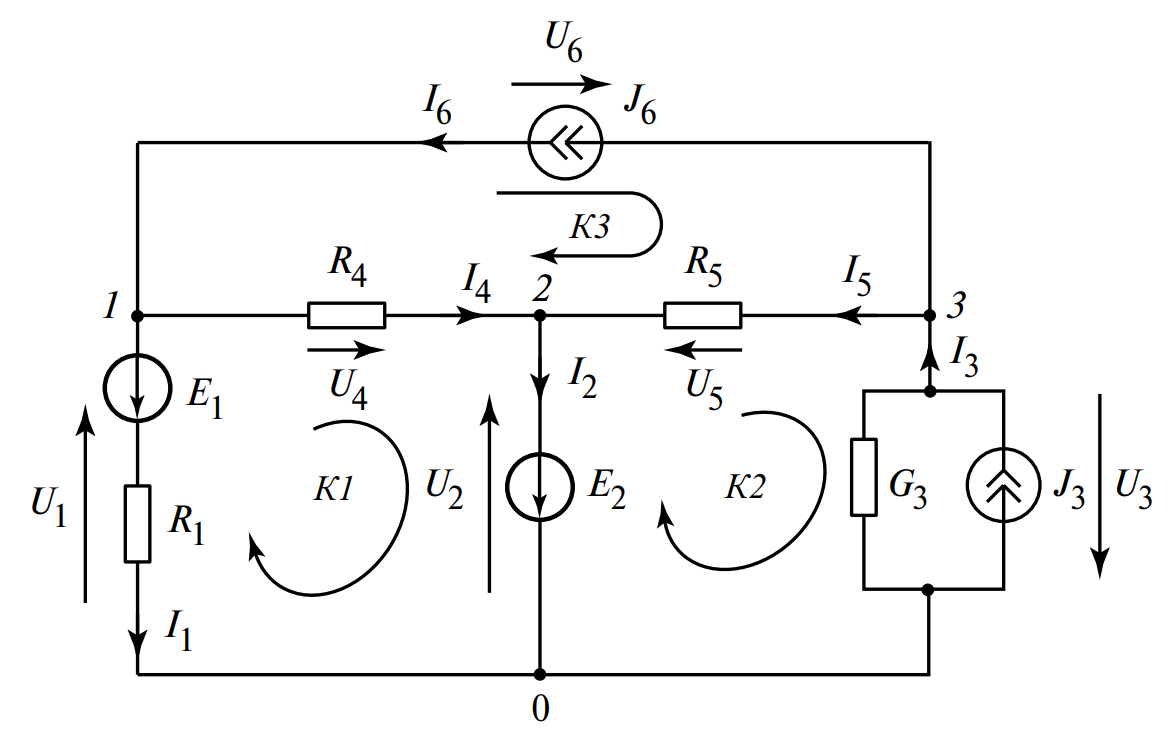
Рис. 1. Электрическая цепь с четырьмя узлами и шестью ветвями.

(На схеме: К1, К2, К3 — независимые контуры; E1, E2 — источники ЭДС; J3, J6 — источники тока; R1, R4, R5, G3 — пассивные элементы)

Рассмотрим пример на Рис. 1. Эта схема имеет $y = 4$ узла (с номерами 0, 1, 2, 3). Следовательно, мы можем составить $y — 1 = 3$ независимых уравнения KCL. Выберем для этого узлы 1, 2 и 3. Приняв условно-положительные направления токов (обозначены стрелками) и считая вытекающие токи положительными, получаем систему:

$$
\begin{cases}
I_1 + I_4 — I_6 = 0 & \text{(для узла 1)} \\
I_2 — I_4 — I_5 = 0 & \text{(для узла 2)} \\
-I_3 + I_5 + I_6 = 0 & \text{(для узла 3)}
\end{cases}
\quad (1)
$$

2. Второй закон Кирхгофа (Закон напряжений, KVL)

Формулировка второго закона Кирхгофа (закон напряжений Кирхгофа) утверждает: алгебраическая сумма напряжений (или ЭДС) на всех элементах, входящих в любой замкнутый контур цепи, равна нулю.

Математически это записывается как:
$$ \sum_{k=1}^{n} U_k = 0 \quad \text{(или} \quad \sum E_k = \sum U_k = \sum R_k I_k \text{)} $$
Этот закон является следствием закона сохранения энергии для электрического поля: работа по перемещению заряда по замкнутому контуру равна нулю.

Для составления уравнений необходимо выбрать независимые контуры и задать для каждого из них направление обхода (например, по часовой стрелке).

Правило знаков: если условно-положительное направление напряжения на элементе (обычно от «+» к «-») совпадает с направлением обхода контура, напряжение берется со знаком «плюс». Если направление противоположно — со знаком «минус». Для источников ЭДС знак «плюс» берется, если направление обхода пересекает источник от «-» к «+».

Количество независимых уравнений, которые можно составить по второму закону, равно $b — (y — 1)$ или $b — y + 1$, где $b$ — общее число ветвей цепи, а $y$ — число узлов.

Для нашей схемы на Рис. 1 ($b = 6$, $y = 4$), число независимых уравнений KVL равно: $6 — 4 + 1 = 3$.

Рассматриваемая схема является планарной (ее можно изобразить на плоскости без пересечения ветвей). В таком случае в качестве независимых контуров удобнее всего выбрать три внутренние ячейки (обозначены К1, К2, К3). Зададим для всех трех контуров единое направление обхода — по часовой стрелке.

Тогда уравнения второго закона Кирхгофа примут вид:

$$
\begin{cases}
U_1 + U_4 — U_2 = 0 & \text{(для контура K1)} \\
U_2 — U_5 + U_3 = 0 & \text{(для контура K2)} \\
-U_4 + U_5 + U_6 = 0 & \text{(для контура K3)}
\end{cases}
\quad (2)
$$

3. Компонентные уравнения и полная система

Законы Кирхгофа (уравнения (1) и (2)) в совокупности дают нам $ (y — 1) + (b — y + 1) = b $ уравнений. В нашем примере это $3 + 3 = 6$ уравнений.

Однако в цепи из $b$ ветвей имеется $2b$ неизвестных величин: $b$ токов ($I_k$) и $b$ напряжений ($U_k$). Для нашей схемы на Рис. 1 это 12 неизвестных ($I_1 \dots I_6$ и $U_1 \dots U_6$).

Для замыкания системы необходимы еще $b$ уравнений. Этими уравнениями являются компонентные уравнения (или законы Ома в обобщенной форме). Они связывают ток и напряжение для каждой отдельной ветви в зависимости от ее состава.

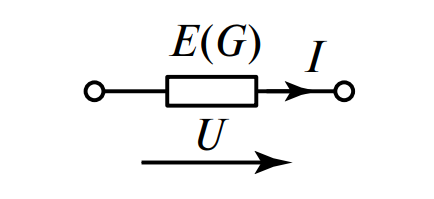
Таблица 1. Компонентные уравнения для основных элементов цепи постоянного тока

Элемент	Обозначение в схеме	Компонентное уравнение
Резистивный элемент		$ U = RI $ (или $ I = GU $, где $ G = 1/R $ — проводимость)
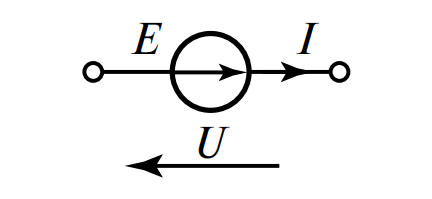
Идеальный источник ЭДС		$ U = E $
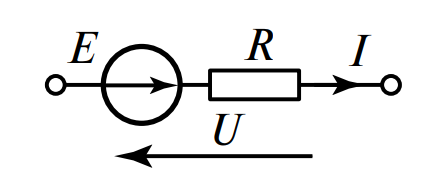
Источник ЭДС (реальный)		$ U = E — RI $
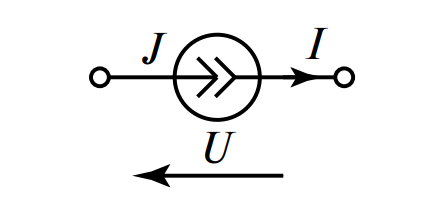
Идеальный источник тока		$ I = J $
Источник тока (реальный)		$ I = J — GU $

Для шести ветвей ($b=6$) на Рис. 1, компонентные уравнения (согласно Таблице 1) имеют вид:

$$
\begin{cases}
U_1 = E_1 — R_1 I_1 & \text{(Ветвь 1: реальный источник ЭДС)} \\
U_2 = E_2 & \text{(Ветвь 2: идеальный источник ЭДС)} \\
I_3 = J_3 — G_3 U_3 & \text{(Ветвь 3: реальный источник тока)} \\
U_4 = R_4 I_4 & \text{(Ветвь 4: резистивный элемент)} \\
U_5 = R_5 I_5 & \text{(Ветвь 5: резистивный элемент)} \\
I_6 = J_6 & \text{(Ветвь 6: идеальный источник тока)}
\end{cases}
\quad (3)
$$

Полная система уравнений

Системы уравнений (1), (2) и (3) вместе формируют полную систему уравнений для рассматриваемой цепи. Она состоит из 12 уравнений (6 уравнений Кирхгофа + 6 компонентных) с 12 неизвестными (6 токов и 6 напряжений). Решение такой системы позволяет найти все параметры цепи.

4. Оптимизация: Гибридная форма уравнений

Решать систему из 12 линейных уравнений вручную крайне затруднительно. На практике для уменьшения размерности системы часто используют гибридный метод.

Суть метода заключается в немедленной подстановке компонентных уравнений (3) в уравнения Кирхгофа (1) и (2). Это позволяет сразу исключить часть переменных. При такой подстановке известные величины (значения ЭДС $E$ и токов источников тока $J$) принято переносить в правую часть уравнений, оставляя слева только члены с неизвестными токами и напряжениями.

Для уравнений KCL (1):

Подставляем компонентные уравнения для $I_3$ и $I_6$ из (3) в систему (1):

$$
\begin{cases}
I_1 + I_4 — (J_6) = 0 & \Rightarrow I_1 + I_4 = J_6 \\
I_2 — I_4 — I_5 = 0 & \Rightarrow I_2 — I_4 — I_5 = 0 \\
-(J_3 — G_3 U_3) + I_5 + (J_6) = 0 & \Rightarrow G_3 U_3 + I_5 = -J_6 + J_3
\end{cases}
\quad (4)
$$

Для уравнений KVL (2):

Подставляем компонентные уравнения для $U_1$, $U_2$, $U_4$, $U_5$ из (3) в систему (2):

$$
\begin{cases}
(E_1 — R_1 I_1) + (R_4 I_4) — (E_2) = 0 & \Rightarrow -R_1 I_1 + R_4 I_4 = E_2 — E_1 \\
(E_2) — (R_5 I_5) + U_3 = 0 & \Rightarrow -R_5 I_5 + U_3 = -E_2 \\
-(R_4 I_4) + (R_5 I_5) + U_6 = 0 & \Rightarrow R_5 I_5 — R_4 I_4 + U_6 = 0
\end{cases}
\quad (5)
$$

Полученная гибридная система из шести уравнений (4) и (5) содержит всего шесть неизвестных: $I_1$, $I_2$, $U_3$, $I_4$, $I_5$, $U_6$. Остальные неизвестные ($U_1$, $U_2$, $I_3$, $U_4$, $U_5$, $I_6$) находятся элементарной подстановкой в компонентные уравнения (3) после решения основной системы.

Преимущества и недостатки метода

Преимущества:
- Универсальность: Метод составления полной системы уравнений применим к абсолютно любой электрической цепи, любой топологии.
- Фундаментальность: Он напрямую основан на незыблемых законах сохранения заряда и энергии.
- Алгоритмичность: Процесс составления уравнений легко формализуется, что удобно для машинного расчета (например, в САПР).
Недостатки:
- Громоздкость: Даже для простой цепи (как на Рис. 1) получается большая система уравнений (6×6 или 12×12).
- Сложность составления: Для сложных непланарных (пространственных) схем выбор независимых контуров становится нетривиальной задачей.
- Риск ошибок: Большое количество уравнений и членов в них повышает вероятность арифметической ошибки при ручном расчете.

Очевидно, что решение даже системы из шести уравнений (4), (5) вручную является трудоемкой задачей. Изучение иных, более формализованных и эффективных способов анализа цепей, таких как метод узловых потенциалов и метод контурных токов, которые не требуют составления столь значительного числа уравнений, составит основу для дальнейшего изучения теории электрических цепей.

5. Постановка задачи анализа электрической цепи

Классическая задача анализа цепи (или задача прямого расчета) формулируется следующим образом:

Дано: Топология (схема) цепи и номинальные параметры всех ее пассивных (R, G, L, C) и активных (E, J) элементов.

Требуется: Определить токи и напряжения на всех (или некоторых) элементах (ветвях) цепи.

Этапы подготовки к решению

На этапе подготовки задачи к решению необходимо выполнить следующие шаги:

Пронумеровать последовательным рядом чисел (1, 2, 3…) все ветви цепи и (0, 1, 2, 3…) все ее узлы. Принято, что номер «0» (ноль) присваивается *базисному* или *опорному* узлу. На практике это часто узел, который соединяется с «землей» (заземляется).
Выбрать условно-положительные направления токов и напряжений для всех ветвей цепи.
- Для пассивных элементов (R) направления $I$ и $U$ обычно выбирают совпадающими (т.н. «согласное» направление).
- Для источников ЭДС и тока эти направления удобно выбирать так, как показано в Таблице 1, т.е. согласуя их с направлениями ЭДС либо токов.

Этап решения и интерпретация результатов

На этапе решения искомые токи и напряжения выражаются через известные параметры с помощью составленной системы уравнений (например, (4) и (5)).

Ключевым моментом является интерпретация полученных знаков.

Если в результате решения найденное значение тока или напряжения оказалось положительным (например, $I_1 = 2 \text{ А}$), это означает, что его истинное физическое направление совпадает с выбранным условно-положительным направлением.
Если значение оказалось отрицательным (например, $I_4 = -1 \text{ А}$), это означает, что истинное направление этого тока противоположно выбранному на схеме условно-положительному направлению.

По направлениям токов и напряжений на идеальных источниках энергии можно судить о режимах их работы (генератор или потребитель). Мощность источника $P = U \cdot I$.

Режимы работы источников

Режим генератора (отдача энергии): Источник отдает энергию в цепь.
- Для источника ЭДС: ток вытекает из положительной клеммы (направления $E$ и $I$ совпадают). Мощность $P = E \cdot I > 0$.
- Для источника тока: напряжение на его клеммах «помогает» току (направления $J$ и $U$ совпадают). Мощность $P = U \cdot J > 0$.
Режим потребителя (потребление энергии): Источник потребляет энергию из цепи (например, зарядка аккумулятора).
- Для источника ЭДС: ток втекает в положительную клемму (направления $E$ и $I$ противоположны). Мощность $P = E \cdot I < 0$.
- Для источника тока: напряжение на его клеммах направлено против тока ($J$ и $U$ противоположны). Мощность $P = U \cdot J < 0$.
Режим холостого хода: Ток через источник ЭДС равен нулю ($I = 0$) или напряжение на источнике тока равно нулю ($U = 0$). Мощность $P = 0$.

6. Пример 1: Расчет цепи на Рис. 1

Решим задачу анализа для цепи на Рис. 1 со следующими параметрами:

$R_1 = 1 \text{ Ом}$
$R_4 = 2 \text{ Ом}$
$R_5 = 2 \text{ Ом}$
$G_3 = 1 \text{ См}$ (Сименс), что эквивалентно $R_3 = 1/G_3 = 1 \text{ Ом}$
$E_1 = 5 \text{ В}$
$E_2 = 1 \text{ В}$
$J_3 = 3 \text{ А}$
$J_6 = 1 \text{ А}$

Подставляя эти численные данные в гибридную систему уравнений (4) и (5), получаем:

Система KCL (из 4):

$$
\begin{cases}
I_1 + I_4 = 1 \\
I_2 — I_4 — I_5 = 0 \\
(1) \cdot U_3 + I_5 = -1 + 3 \Rightarrow 1U_3 + I_5 = 2
\end{cases}
$$

Система KVL (из 5):

$$
\begin{cases}
-1I_1 + 2I_4 = 1 — 5 \Rightarrow -1I_1 + 2I_4 = -4 \\
-2I_5 + U_3 = -1 \\
2I_5 — 2I_4 + U_6 = 0
\end{cases}
$$

Решая эту систему из шести линейных уравнений (например, методом подстановки или матричным методом), находим шесть основных неизвестных:

$I_1 = 2 \text{ А}$
$I_2 = 0 \text{ А}$
$I_4 = -1 \text{ А}$
$I_5 = 1 \text{ А}$
$U_3 = 1 \text{ В}$
$U_6 = -4 \text{ В}$

Теперь, используя компонентные уравнения (3), находим оставшиеся шесть переменных:

$$ U_1 = E_1 — R_1 I_1 = 5 — 1 \cdot (2) = 3 \text{ В} $$
$$ U_2 = E_2 = 1 \text{ В} $$
$$ I_3 = J_3 — G_3 U_3 = 3 — 1 \cdot (1) = 2 \text{ А} $$
$$ U_4 = R_4 I_4 = 2 \cdot (-1) = -2 \text{ В} $$
$$ U_5 = R_5 I_5 = 2 \cdot (1) = 2 \text{ В} $$
$$ I_6 = J_6 = 1 \text{ А} $$

Анализ результатов и режимов работы источников

Анализ направлений:
- Токи $I_1, I_2, I_3, I_5, I_6$ и напряжения $U_1, U_2, U_3, U_5$ имеют положительные или нулевые значения. Это значит, что их истинные направления совпадают с условно-положительными, выбранными на Рис. 1.
- Ток $I_4$ и напряжения $U_4, U_6$ имеют отрицательные значения. Это значит, что их истинные направления противоположны тем, что выбраны на Рис. 1. (Например, ток $I_4$ на самом деле течет от узла 2 к узлу 1).
Анализ режимов работы источников:
- Источник ЭДС $E_1$: Через него протекает ток $I_1 = 2 \text{ А}$. Направление тока совпадает с направлением ЭДС ($I_1 > 0$). Мощность $P_1 = E_1 \cdot I_1 = 5 \text{ В} \cdot 2 \text{ А} = 10 \text{ Вт}$. Источник генерирует энергию.
- Источник ЭДС $E_2$: Ток через него $I_2 = 0 \text{ А}$. Источник работает в режиме холостого хода, не потребляя и не генерируя энергию.
- Источник тока $J_3$: Напряжение на нем $U_3 = 1 \text{ В}$. Направление напряжения совпадает с направлением тока ($U_3 > 0$). Мощность $P_3 = U_3 \cdot J_3 = 1 \text{ В} \cdot 3 \text{ А} = 3 \text{ Вт}$. Источник генерирует энергию.
- Источник тока $J_6$: Напряжение на нем $U_6 = -4 \text{ В}$. Напряжение направлено против направления тока ($U_6 < 0$). Мощность $P_6 = U_6 \cdot I_6 = -4 \text{ В} \cdot 1 \text{ А} = -4 \text{ Вт}$. Источник потребляет энергию (работает как нагрузка).

7. Сравнение Первого и Второго законов Кирхгофа

Характеристика	Первый закон Кирхгофа (KCL)	Второй закон Кирхгофа (KVL)
Фундаментальный принцип	Закон сохранения электрического заряда	Закон сохранения энергии
Сущность	Алгебраическая сумма токов в узле равна нулю. ($ \sum I_k = 0 $)	Алгебраическая сумма напряжений в контуре равна нулю. ($ \sum U_k = 0 $)
Объект применения	Узел (точка соединения трех и более ветвей)	Замкнутый контур (любой замкнутый путь в цепи)
Количество независимых уравнений	$ y — 1 $ (где $y$ — число узлов)	$ b — y + 1 $ (где $b$ — число ветвей)
Основная переменная	Ток ($I$)	Напряжение ($U$)
Основа для метода	Метод узловых потенциалов (МУП)	Метод контурных токов (МКТ)

8. Интересные факты о законах Кирхгофа

Раннее открытие: Густав Кирхгоф сформулировал эти законы в 1845 году, будучи 21-летним студентом Кёнигсбергского университета, в рамках своей семинарской работы.
Применение в AC цепях: Законы Кирхгофа полностью применимы и для цепей переменного тока. Для этого расчет цепи ведется в комплексной форме: вместо сопротивлений $R$ используются комплексные импедансы $Z$, а токи и напряжения представляются в виде комплексных чисел (амплитуд и фаз).
Границы применимости: Законы Кирхгофа являются основой теории цепей с сосредоточенными параметрами. Они перестают быть точными на очень высоких (СВЧ) частотах, когда длина волны становится сопоставимой с размерами элементов цепи. В таких случаях необходимо использовать теорию цепей с распределенными параметрами и полные уравнения Максвелла.
Связь с уравнениями Максвелла: KCL (закон токов) является частным случаем уравнения непрерывности для тока ($ \text{div} \vec{j} = -\frac{\partial \rho}{\partial t} $) в предположении, что заряд в узле не накапливается ($ \frac{\partial \rho}{\partial t} = 0 $).
Связь с законом Фарадея: KVL (закон напряжений) является частным случаем закона электромагнитной индукции Фарадея ($ \oint \vec{E} \cdot d\vec{l} = -\frac{\partial \Phi}{\partial t} $). Он справедлив, когда можно пренебречь изменением магнитного потока ($ \Phi $), пронизывающего контур.

9. Часто задаваемые вопросы (FAQ)

1. Что такое «ветвь», «узел» и «контур»?

Ветвь — это участок цепи, состоящий из одного или нескольких последовательно соединенных элементов, заключенный между двумя узлами. По всем элементам одной ветви протекает один и тот же ток.

Узел — это точка в схеме, где соединяются три или более ветви. (Точка соединения двух ветвей узлом обычно не считается, т.к. это просто последовательное соединение).

Контур — это любой замкнутый путь, проходящий по нескольким ветвям и узлам цепи.

2. Почему для KCL берется $y — 1$ узлов, а не все $y$?

Потому что уравнение для последнего, $y$-го узла, не является независимым. Оно всегда может быть получено путем сложения или вычитания уравнений для всех остальных $y — 1$ узлов. Если бы мы включили его в систему, она была бы вырожденной (имела бы бесконечное множество решений).

3. Что будет, если я выберу другое направление обхода контура для KVL?

Результат расчета не изменится. Если вы выберете направление обхода против часовой стрелки (вместо «по часовой»), все знаки в вашем уравнении для этого контура изменятся на противоположные (например, $ -U_1 — U_4 + U_2 = 0 $). Это эквивалентно умножению исходного уравнения на -1, что не меняет решения системы.

4. Что такое «планарная» схема?

Планарная (или плоская) схема — это схема, которую можно нарисовать на плоскости (на листе бумаги) так, чтобы ее ветви не пересекались друг с другом нигде, кроме как в узлах. Схема на Рис. 1 является планарной. Непланарная схема (например, пространственный «каркас куба») не может быть так изображена.

5. Можно ли использовать эти законы, если в цепи есть конденсаторы или катушки индуктивности?

Да, безусловно. Законы Кирхгофа универсальны.

— Для цепей переменного тока (AC): Расчет ведется в комплексных числах, используя импедансы ($ Z_R = R $, $ Z_L = j\omega L $, $ Z_C = 1/(j\omega C) $).

— Для расчета переходных процессов (DC): Используются дифференциальные компонентные уравнения ($ u_L(t) = L \frac{di(t)}{dt} $, $ i_C(t) = C \frac{du(t)}{dt} $). В этом случае полная система уравнений становится системой дифференциальных уравнений.

Заключение

Первый и второй законы Кирхгофа являются основой всей теории электрических цепей. Они предоставляют универсальный и фундаментальный метод для математического описания любых процессов в электрических цепях.

Составление полной системы уравнений, включающей уравнения по законам Кирхгофа (KCL и KVL) и компонентные уравнения, является наиболее строгим, хотя и самым громоздким методом анализа. Как показано в примере, даже для простой схемы он приводит к объемной системе уравнений.

Этот метод служит теоретической базой для разработки более эффективных и формализованных алгоритмов расчета, таких как метод узловых потенциалов (основан на KCL) и метод контурных токов (основан на KVL), которые позволяют значительно сократить число итоговых уравнений.

Нормативная база

Терминология, определения и графические обозначения в электрических схемах регламентируются государственными и межгосударственными стандартами.

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий» — Устанавливает основные термины (ток, напряжение, узел, ветвь, контур, источник ЭДС и т.д.) и их определения в области электротехники.
ГОСТ 2.721-74 «Единая система конструкторской документации. Обозначения условные графические в схемах. Обозначения общего применения» — Регламентирует условные графические обозначения элементов на схемах (резисторы, источники и т.д.).
IEC 60050 «International Electrotechnical Vocabulary (IEV)» — Международный электротехнический словарь, который является основой для гармонизации терминологии во многих национальных стандартах.

Законы Кирхгофа: полная система уравнений для анализа электрических цепей