Работа идеального резистора в цепи синусоидального тока

Содержание страницы

1. Закон Ома в цепях синусоидального тока
2. Энергетические процессы: Мгновенная и активная мощность
3. Графическая интерпретация процессов
4. Таблица сравнения характеристик элементов цепи
5. Интересные факты о резистивных элементах
6. FAQ: Часто задаваемые вопросы
Заключение

В электротехнике и теории цепей понятие «идеальный резистивный элемент» (или идеальный резистор) является фундаментальной абстракцией. Это элемент электрической цепи, основным и единственным свойством которого является необратимое преобразование электрической энергии в другие виды энергии (преимущественно в тепловую или световую). В отличие от реактивных элементов (катушек индуктивности и конденсаторов), идеальный резистор не накапливает энергию в виде магнитного или электрического поля.

Важно понимать: В реальной жизни абсолютно «идеальных» резисторов не существует. Любой реальный проводник обладает паразитной индуктивностью и емкостью. Однако на низких и средних частотах этими параметрами можно пренебречь, рассматривая элемент как чисто активное сопротивление \( R \).

1. Закон Ома в цепях синусоидального тока

Мгновенные значения напряжения \( u(t) \) и тока \( i(t) \) в идеальном резистивном элементе неразрывно связаны законом Ома. Как было отмечено в предыдущих разделах курса ТОЭ (теоретических основ электротехники), эта связь линейна и безынерционна:

u(t) = R \cdot i(t) \quad \text{или} \quad i(t) = G \cdot u(t)

Где:

\( R = \frac{1}{G} \) — активное электрическое сопротивление, измеряемое в Омах (Ом);
\( G \) — электрическая проводимость идеального резистивного элемента (резистора), измеряемая в Сименсах (См).

Рассмотрим поведение системы при воздействии гармонического (синусоидального) сигнала. Пусть ток в цепи изменяется по закону:

i(t) = I_m \sin(\omega t + \psi_i)

Тогда, согласно закону Ома, мгновенное значение напряжения будет определяться выражением:

u(t) = R \cdot I_m \sin(\omega t + \psi_i) = U_m \sin(\omega t + \psi_u)

1.1. Фазовые соотношения

Ключевой особенностью активного сопротивления является отсутствие сдвига фаз. Напряжение \( u(t) \) совпадает по фазе с током \( i(t) \). Математически это выражается равенством начальных фаз:

\psi_u = \psi_i

Следовательно, угол сдвига фаз \( \phi \), определяемый как разность фаз напряжения и тока, равен нулю:
\( \phi = \psi_u — \psi_i = 0 \).

1.2. Амплитудные соотношения

Амплитуда напряжения \( U_m \) связана с амплитудой тока \( I_m \) через сопротивление или проводимость элемента:

U_m = R \cdot I_m = \frac{I_m}{G}

2. Энергетические процессы: Мгновенная и активная мощность

Энергетическая характеристика цепи описывается величиной \( p(t) = u(t) \cdot i(t) \), которая называется мгновенной мощностью.
Используя соотношение \( u(t) = R \cdot i(t) \), мы можем записать:

p(t) = R \cdot i^2(t) = G \cdot u^2(t)

Из квадратичной зависимости видно, что мгновенная мощность в резисторе всегда положительна (или равна нулю), независимо от направления тока. Это физически означает, что резистор всегда потребляет энергию от источника, необратимо преобразуя её в тепло.

2.1. Математический вывод формулы мощности

Для синусоидального режима подставим выражения для тока и напряжения в формулу мощности:

p(t) = U_m \sin(\omega t + \psi_u) \cdot I_m \sin(\omega t + \psi_i)

Используя тригонометрическую формулу произведения синусов \( \sin\alpha \cdot \sin\beta = \frac{1}{2}[\cos(\alpha-\beta) — \cos(\alpha+\beta)] \), получаем разложение на две составляющие:

p(t) = \frac{U_m I_m}{2} [\cos(\psi_u — \psi_i) — \cos(2\omega t + \psi_u + \psi_i)]

Поскольку в резисторе \( \psi_u = \psi_i \) и \( \phi = 0 \), выражение упрощается. Учитывая, что действующие значения \( U = \frac{U_m}{\sqrt{2}} \) и \( I = \frac{I_m}{\sqrt{2}} \), их произведение \( UI = \frac{U_m I_m}{2} \).
Таким образом:

p(t) = UI [1 — \cos(2\omega t + 2\psi_i)]

Или в более общем виде через угол сдвига фаз \( \phi \):

p(t) = UI \cos\phi — UI \cos(2\omega t + \psi_u + \psi_i)

2.2. Активная мощность (P)

Мгновенная мощность колеблется с удвоенной частотой \( 2\omega \). Однако на практике важнее среднее значение мощности за период \( T \), которое называется активной мощностью. Она характеризует среднюю скорость необратимого преобразования энергии.

Математически активная мощность \( P \) определяется как интеграл за период:

P = p_{ср}(t) = \frac{1}{T} \int_{0}^{T} p(t) dt

Так как интеграл от косинусоиды двойной частоты за период равен нулю (площади положительных и отрицательных полуволн компенсируют друг друга), остается только постоянная составляющая:

P = \frac{1}{T} \int_{0}^{T} \frac{U_m I_m}{2} \cos\phi \, dt = UI \cos\phi

Для резистивного элемента, где \( \cos\phi = \cos(0) = 1 \), формула принимает классический вид:

P = UI = I^2 R = \frac{U^2}{R}

Единицей измерения активной \( P \) и мгновенной \( p(t) \) мощностей является ватт (Вт).

3. Графическая интерпретация процессов

Для наглядного представления процессов рассмотрим графики изменений во времени и векторную диаграмму.

3.1. Временные диаграммы

На рисунке 1 представлены графики зависимостей напряжения \( u(t) \), тока \( i(t) \) и мгновенной мощности \( p(t) \).

Рис. 1. Графики зависимостей u(t), i(t) и р(t) в резистивном элементе

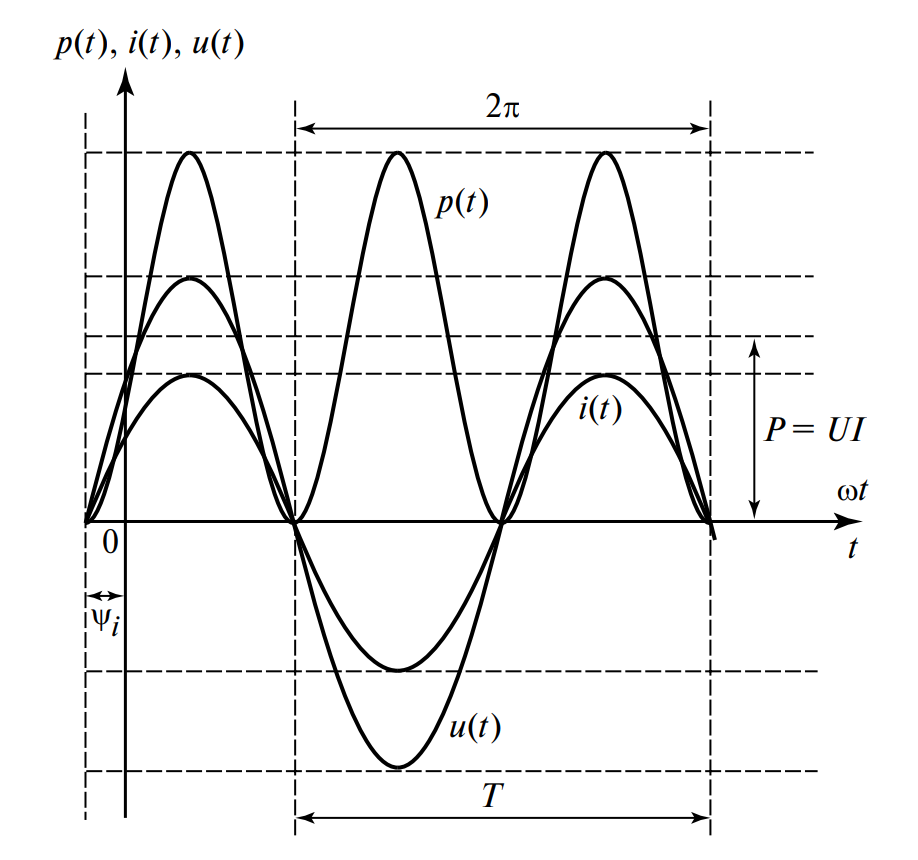
Анализ графика (Рис. 1):

Кривые \( u(t) \) и \( i(t) \) синфазны: они одновременно достигают максимумов и одновременно проходят через ноль.
Кривая мгновенной мощности \( p(t) \) расположена только в положительной области (над осью времени \( t \)). Это подтверждает тезис о том, что резистор только потребляет энергию.
Частота пульсаций мощности в два раза выше частоты тока.
Средняя линия пульсаций мощности соответствует значению активной мощности \( P = UI \).

3.2. Векторная диаграмма

Векторные диаграммы — мощный инструмент анализа цепей переменного тока. На рисунке 2 показана диаграмма для идеального резистора.

Рис. 2. Векторная диаграмма напряжения и тока в резистивном элементе

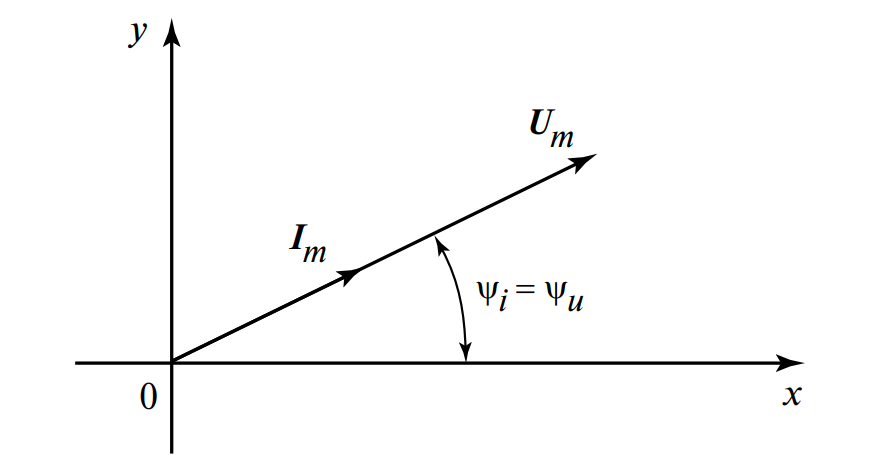
На диаграмме изображены векторы, соответствующие амплитудам тока \( I_m \) и напряжения \( U_m \). Так как сдвиг фаз отсутствует (\( \psi_i = \psi_u \)), векторы направлены в одну сторону (коллинеарны).

Примечание: На векторных диаграммах вместо векторов амплитуд (\( I_m, U_m \)) часто и вполне допустимо изображать векторы действующих значений (\( I, U \)). Они будут иметь то же направление, но их длина будет в \( \sqrt{2} \approx 1.41 \) раз меньше амплитудных.

4. Таблица сравнения характеристик элементов цепи

Для понимания уникальности резистивного элемента сравним его с реактивными компонентами.

Характеристика	Резистор (R)	Индуктивность (L)	Емкость (C)
Основной закон	\( u = Ri \)	\( u = L \frac{di}{dt} \)	\( i = C \frac{du}{dt} \)
Сдвиг фаз (\(\phi\))	0 (фазы совпадают)	+90° (напряжение опережает)	-90° (ток опережает)
Энергия	Необратимо преобразуется (тепло)	Накапливается в магнитном поле	Накапливается в электрическом поле
Зависимость от частоты	Нет (в идеальном случае)	\( X_L = \omega L \) (растет)	\( X_C = \frac{1}{\omega C} \) (падает)
Мгновенная мощность	Всегда \(\ge 0\)	Знакопеременная (обмен энергией)	Знакопеременная (обмен энергией)

5. Интересные факты о резистивных элементах

Реостатное торможение. Самые мощные резисторы используются в тормозных системах электропоездов. Они превращают кинетическую энергию многотонного состава в тепло при реостатном торможении.
Тепловой шум. Даже идеальный резистор является источником шума. Тепловой шум (шум Джонсона-Найквиста) возникает из-за хаотического движения носителей заряда и пропорционален температуре и сопротивлению.
Единица «Мо». Единица измерения проводимости «Сименс» ранее называлась «Мо» (Mho) — это слово «Ohm», написанное задом наперед.
Скин-эффект. При очень высоких частотах ток вытесняется на поверхность проводника (скин-эффект), из-за чего эффективное сопротивление провода возрастает по сравнению с сопротивлением постоянному току.
Паразитная индуктивность. Абсолютно чистого активного сопротивления в природе не существует; даже прямой кусок провода имеет индуктивность.
Стандартные ряды. Стандартные ряды номиналов резисторов (E6, E12, E24 и т.д.) построены по логарифмическому закону, чтобы перекрывать диапазон с одинаковой относительной погрешностью.
Сверхпроводимость. При температуре абсолютного нуля (-273.15°C) сопротивление некоторых материалов исчезает полностью. Это явление сверхпроводимости, где \( R=0 \), и закон Ома в привычном виде перестает работать.

6. FAQ: Часто задаваемые вопросы

Вопрос 1: Почему мгновенная мощность колеблется с удвоенной частотой?

Это происходит из-за того, что мощность зависит от квадрата тока (\( i^2 \)). Ток имеет положительную и отрицательную полуволну за один период, но при возведении в квадрат обе полуволны становятся положительными. В результате за один период изменения тока (Т) мощность успевает достигнуть максимума дважды.

Вопрос 2: Чем отличается активная мощность от полной?

Активная мощность (\( P \)) — это та часть энергии, которая безвозвратно расходуется (на тепло, работу). Полная мощность (\( S \)) включает в себя также реактивную мощность, которая «гуляет» между источником и реактивными элементами, не совершая полезной работы. Для идеального резистора \( P = S \).

Вопрос 3: Почему на векторной диаграмме угол между током и напряжением равен нулю?

Это физическое свойство резистора. Ток в нем возникает мгновенно при приложении напряжения, нет инерции, как в катушке (препятствующей изменению тока) или конденсаторе (требующем времени на зарядку).

Вопрос 4: Зависят ли формулы от частоты сети 50 Гц или 60 Гц?

Нет, приведенные формулы универсальны для любой частоты \( \omega \). Однако в реальных резисторах при очень высоких частотах (МГц, ГГц) сопротивление может меняться из-за паразитных эффектов.

Вопрос 5: Можно ли применять формулу \( P = I^2 R \) для несинусоидального тока?

Да, эта формула справедлива для мгновенных значений любого тока. Если же речь идет о средних значениях за период, то нужно использовать действующее (среднеквадратичное) значение тока \( I \).

Заключение

Рассмотрение синусоидального тока в идеальном резистивном элементе является базой для понимания процессов в цепях переменного тока. Мы выяснили, что резистор — это «потребитель» энергии, где ток и напряжение совпадают по фазе, а активная мощность является мерой тепловых потерь. Понимание этих фундаментальных принципов и умение оперировать векторными диаграммами и формулами мгновенной мощности необходимо любому специалисту в области электротехники и электроники для расчета более сложных цепей R-L-C.

Нормативная база

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Определяет базовые понятия: резистивный элемент, активная мощность, электрическое сопротивление.
ГОСТ 2.728-74 «Единая система конструкторской документации. Обозначения условные графические в схемах. Резисторы, конденсаторы». Регламентирует графическое изображение резисторов на схемах.
ГОСТ 1494-77 «Электротехника. Буквенные обозначения основных величин». Устанавливает символы \( R, U, I, P, \phi \) и другие.

Список литературы:

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2023.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Том 1. — Л.: Энергоиздат, 1981.
Атабеков Г.И. Основы теории цепей. — М.: Энергия, 1969.