Симметричная нагрузка в трехфазной цепи: Звезда и Треугольник

Содержание страницы

1. Соединение нагрузки звездой с нулевым проводом
2. Соединение равномерной нагрузки звездой без нулевого провода
3. Соединение равномерной нагрузки треугольником
4. Сравнительный анализ: Звезда vs Треугольник
5. Интересные факты о трехфазных цепях
6. FAQ: Часто задаваемые вопросы
Заключение

Трехфазная цепь с симметричной нагрузкой — это идеальный режим работы электросети, при котором сопротивления всех трех фаз потребителя равны по величине и характеру.

Исторически фундамент этой теории заложил М.О. Доливо-Добровольский в 1880-х годах, доказав эффективность передачи энергии тремя проводами. Понимание этих процессов критически важно для инженеров, так как большинство промышленных двигателей работает именно в этом режиме.

Приемники в трехфазной цепи традиционно соединяются двумя основными способами: «звездой» или «треугольником». Рассмотрим подробно физику процессов и математический аппарат для каждого вида соединений в условиях симметрии.

1. Соединение нагрузки звездой с нулевым проводом

Это соединение является базовым в системе низковольтного электроснабжения промышленных предприятий и гражданских объектов (например, в жилых домах). В данной конфигурации источники энергии также соединяются звездой, а нейтральные (нулевые) точки источников и приемников — точки $ N $ и $ n $ соответственно — соединяются нулевым проводом (см. Рисунок 1).

Ключевая особенность: Наличие нулевого провода обеспечивает жесткую привязку потенциалов, что позволяет подключать к фазам приемника как симметричную, так и несимметричную нагрузку, сохраняя равенство фазных напряжений.

Токи в фазах определяются по закону Ома для участка цепи: $$ \dot{I}_A = \frac{\dot{U}_A}{Z_A}; \quad \dot{I}_B = \frac{\dot{U}_B}{Z_B}; \quad \dot{I}_C = \frac{\dot{U}_C}{Z_C} $$ где \( \dot{U} \) — фазное напряжение, а \( Z \) — полное комплексное сопротивление фазы.

Ток в нулевом проводе согласно первому закону Кирхгофа равен геометрической (векторной) сумме фазных токов:

\dot{I}_N = \dot{I}_A + \dot{I}_B + \dot{I}_C

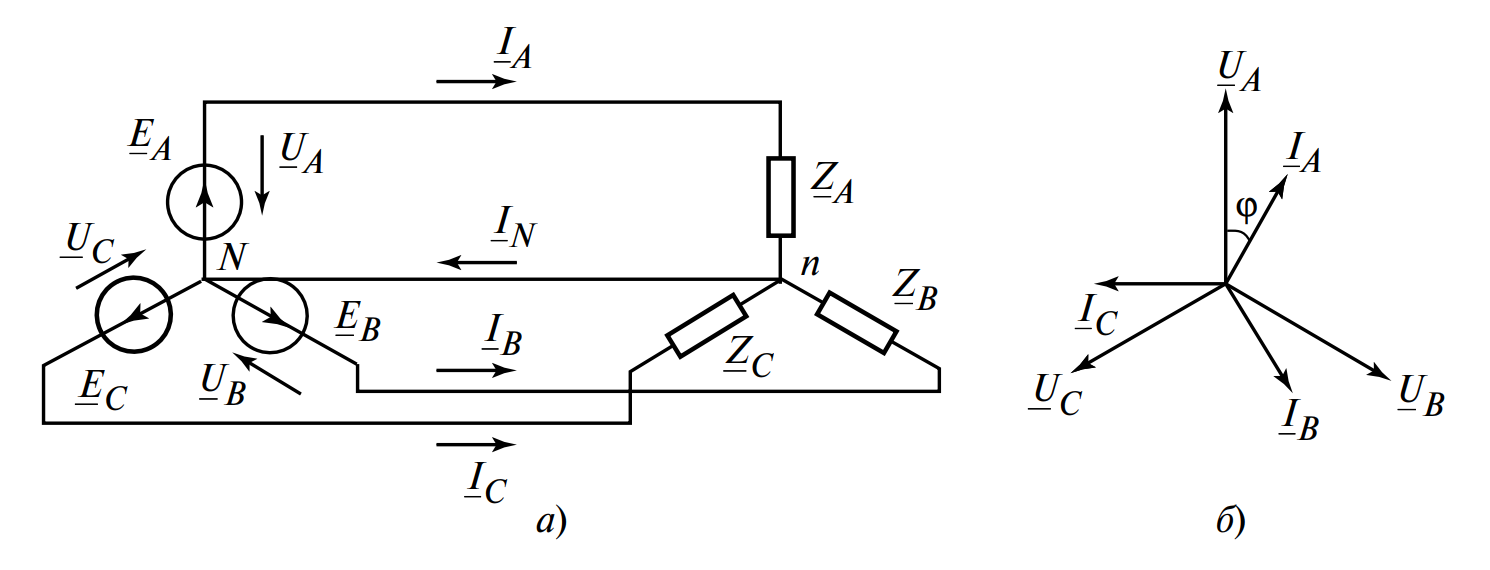
Рисунок 1. Соединение нагрузки звездой с нулевым проводом: а — схема соединений (показаны точки N и n); б — векторная диаграмма токов и напряжений.

Аналогия: Представьте три насоса (фазы), качающие воду в один общий резервуар, из которого вода уходит по одной большой трубе (нулевой провод). Если все насосы работают идеально синхронно и одинаково (симметрия), поток воды стабилизируется.

Векторная диаграмма

Векторная диаграмма токов для равномерной нагрузки представлена на рис. 1, б. При симметричной нагрузке векторы токов образуют замкнутый треугольник (при сложении), что приводит к важному выводу.

В случае строго симметричных потребителей (равенство сопротивлений $ Z_A = Z_B = Z_C $) четвертый провод становится электрически «лишним», так как ток в нулевом проводе $ \dot{I}_N $ будет равен нулю.

Пример расчёта №1 (Четырехпроводная цепь)

Дано: Линейное напряжение четырехпроводной трехфазной цепи (см. рис. 1, а) $ U_{line} = 380 $ В. Фазное сопротивление симметричного приемника $ Z = (8 + j6) $ Ом.
Найти: Фазные напряжения и токи.

Решение:

1. Определяем фазное напряжение. Для соединения звездой оно в $ \sqrt{3} $ раз меньше линейного:

U_{ph} = \frac{U_{line}}{\sqrt{3}} = \frac{380}{1.73} \approx 220 \text{ В}

2. Запишем напряжения в фазах приемника в комплексной форме (принимая фазу А за начало отсчета):

$ \dot{U}_A = 220 $ В
$ \dot{U}_B = 220 \cdot e^{-j120^{\circ}} $ В (или $ 220 \angle -120^{\circ} $)
$ \dot{U}_C = 220 \cdot e^{j120^{\circ}} $ В (или $ 220 \angle 120^{\circ} $)

3. Рассчитаем токи в фазах:

\dot{I}_A = \frac{\dot{U}_A}{Z_A} = \frac{220}{8 + j6} $$ Переведем сопротивление в показательную форму: \( 8 + j6 = \sqrt{8^2+6^2} \cdot e^{j \arctan(6/8)} = 10 \angle 36.86^{\circ} \) $$ \dot{I}_A = \frac{220 \angle 0^{\circ}}{10 \angle 36.86^{\circ}} = 22 \angle -36.86^{\circ} \text{ А}

Аналогично для других фаз, учитывая сдвиг фаз на 120°:

$ \dot{I}_B = 22 \angle (-36.86^{\circ} — 120^{\circ}) = 22 \angle -156.86^{\circ} $ А
$ \dot{I}_C = 22 \angle (-36.86^{\circ} + 120^{\circ}) = 22 \angle 86.14^{\circ} $ А

Ответ: Ток в нулевом проводе $ \dot{I}_N = 0 $.

2. Соединение равномерной нагрузки звездой без нулевого провода

В случае гарантированно равномерной нагрузки часто применяют более экономичную трехпроводную систему (см. Рисунок 2). Классическим примером такой нагрузки являются трехфазные асинхронные двигатели, широко распространенные в промышленности, где обмотки статора абсолютно идентичны.

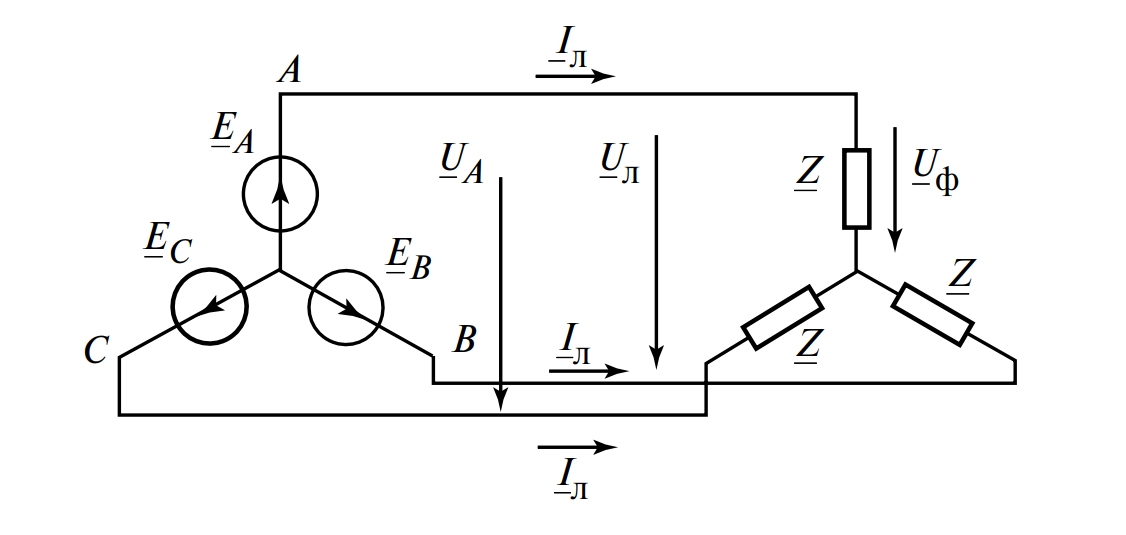
Рисунок 2. Трехпроводная система (соединение звезда без нейтрали).

Расчет симметричной трехфазной системы без нулевого провода существенно упрощается и сводится к расчету параметров только одной фазы:

Фазное напряжение: $ U_{ph} = \frac{U_{line}}{\sqrt{3}} $
Фазный ток: $ I_{ph} = \frac{U_{ph}}{Z} $

В комплексной форме токи в фазах выражаются через поворотный множитель:

\dot{I}_B = \dot{I}_A \cdot e^{-j120^{\circ}}; \quad \dot{I}_C = \dot{I}_A \cdot e^{j120^{\circ}} \quad

Важно: В трехпроводной системе с равномерной нагрузкой, соединенной звездой, линейные токи всегда равны фазным токам: $ I_{line} = I_{ph} $.

Пример расчёта №2 (Трехпроводная цепь)

Дано: Линейное напряжение (см. рис. 2) $ U_{line} = 380 $ В. Фазное сопротивление симметричного приемника $ Z = (8 + j6) $ Ом.
Найти: Фазные токи.

Решение:

Фазное напряжение $ U_{ph} = 220 $ В.

Токи в фазах рассчитываются аналогично предыдущему примеру:

\dot{I}_A = \frac{220}{8 + j6} = 22 \angle -36.86^{\circ} \text{ А}

Остальные токи сдвинуты на 120 градусов:

$ \dot{I}_B = 22 \angle -156.86^{\circ} $ А
$ \dot{I}_C = 22 \angle 86.14^{\circ} $ А

Примечание: Фазные токи остались такими же, как и в примере №1, что подтверждает идентичность режимов работы при симметрии.

3. Соединение равномерной нагрузки треугольником

При соединении нагрузки треугольником (см. Рисунок 3, а) каждая фаза приемника подключается непосредственно к линейным проводам. Следовательно, между зажимами фазы нагрузки действует полное линейное напряжение.

В соединении треугольником линейное напряжение является одновременно фазным для приемника:
$$ U_{ph} = U_{line} $$

Токи в фазах приемника (в сторонах треугольника) находят по закону Ома:

\dot{I}_{AB} = \frac{\dot{U}_{AB}}{Z_{AB}}; \quad \dot{I}_{BC} = \frac{\dot{U}_{BC}}{Z_{BC}}; \quad \dot{I}_{CA} = \frac{\dot{U}_{CA}}{Z_{CA}} \quad

Направления токов:

Линейные токи считаются положительными, если направлены от источника к приемнику.
Положительные направления фазных токов условно выбираются по часовой стрелке: от А к В, от В к С, от С к А.

Линейные токи (в подводящих проводах) находятся из первого закона Кирхгофа для узлов треугольника:

\dot{I}_A = \dot{I}_{AB} — \dot{I}_{CA}; \quad \dot{I}_B = \dot{I}_{BC} — \dot{I}_{AB}; \quad \dot{I}_C = \dot{I}_{CA} — \dot{I}_{BC} \quad

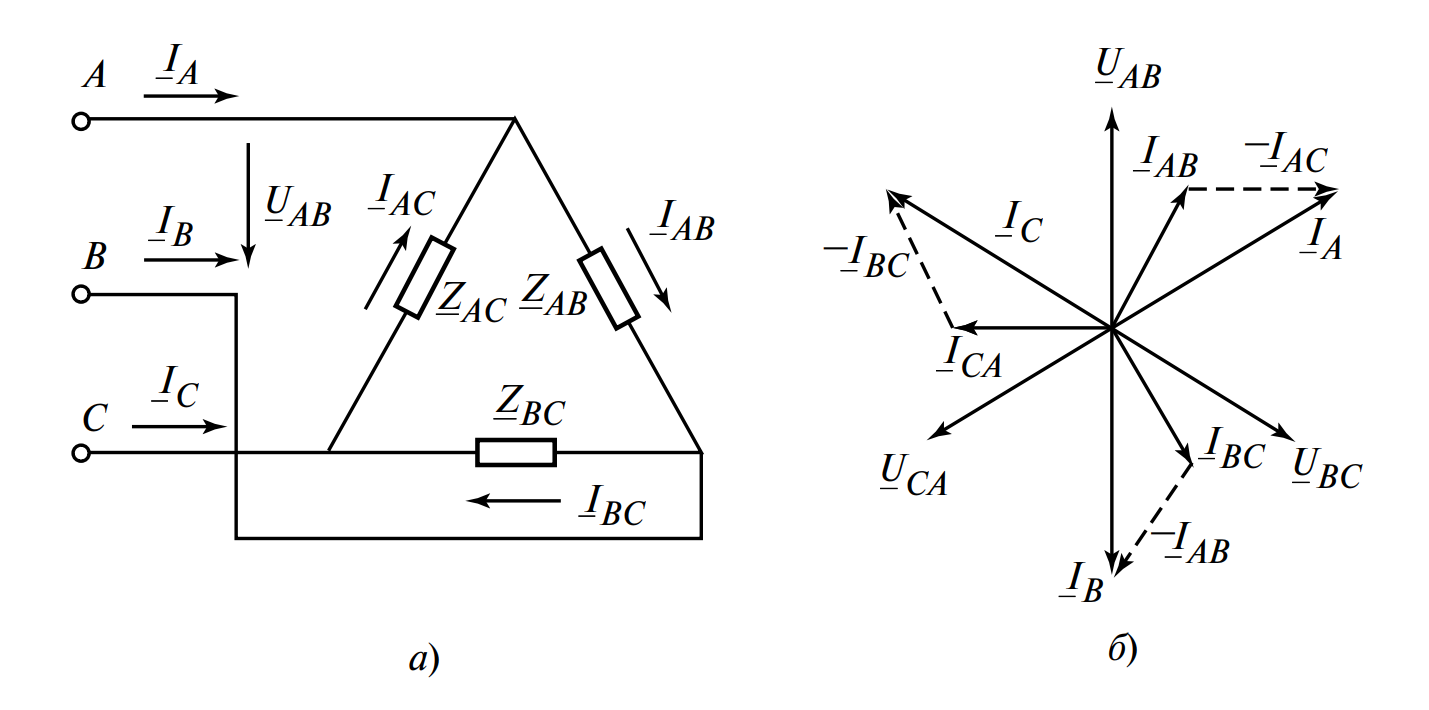
Рисунок 3. Соединение нагрузки треугольником: а — схема соединений; б — векторная диаграмма токов и напряжений.

Соотношения при равномерной нагрузке

Если нагрузка равномерна ($ Z_{AB} = Z_{BC} = Z_{CA} = Z $), фазные токи образуют симметричную систему. Линейные токи также образуют симметричную звезду. Между модулями (величинами) линейных и фазных токов существует фундаментальное соотношение:

I_{line} = \sqrt{3} \cdot I_{ph}

Пример расчёта №3 (Треугольник)

Дано: Фазная ЭДС генератора (обмотки соединены звездой) равна 220 В. Симметричный приемник соединен треугольником. Сопротивления фаз $ Z = (12 + j12) $ Ом.
Определить: Фазные и линейные токи.

Решение:

1. Напряжение генератора фазное $ U_A = 220 $ В. Так как генератор в звезде, линейное напряжение сети:

U_{line} = 220 \cdot \sqrt{3} \approx 380 \text{ В}

Для приемника, соединенного в треугольник, это напряжение является фазным. Запишем линейные напряжения (они же фазные для нагрузки) в векторной форме:

$ \dot{U}_{AB} = 380 \angle 30^{\circ} $ В
$ \dot{U}_{BC} = 380 \angle -90^{\circ} $ В
$ \dot{U}_{CA} = 380 \angle 150^{\circ} $ В

2. Вычислим фазные токи (токи внутри треугольника):

Сопротивление \( Z = 12 + j12 \approx 16.97 \angle 45^{\circ} \) Ом. $$ \dot{I}_{AB} = \frac{380 \angle 30^{\circ}}{16.97 \angle 45^{\circ}} = 22.45 \angle -15^{\circ} \text{ А} $$

Аналогично:

$ \dot{I}_{BC} = 22.45 \angle (-90^{\circ} — 45^{\circ}) = 22.45 \angle -135^{\circ} $ А
$ \dot{I}_{CA} = 22.45 \angle (150^{\circ} — 45^{\circ}) = 22.45 \angle 105^{\circ} $ А

3. Вычислим линейные токи:

\dot{I}_A = \dot{I}_{AB} — \dot{I}_{CA} = 22.45 \angle -15^{\circ} — 22.45 \angle 105^{\circ} $$ Результат вычисления: $$ \dot{I}_A \approx 39 \angle -45^{\circ} \text{ А}

Остальные линейные токи равны по модулю (39 А) и сдвинуты на 120°:

$ \dot{I}_B = 39 \angle -165^{\circ} $ А
$ \dot{I}_C = 39 \angle 75^{\circ} $ А

4. Сравнительный анализ: Звезда vs Треугольник

Для наглядности сведем основные различия симметричных режимов в таблицу.

Характеристика	Соединение Звезда ($ \lambda $)	Соединение Треугольник ($ \Delta $)
Напряжение на фазе нагрузки	В $ \sqrt{3} $ раз меньше линейного ($ U_{ph} = U_L / \sqrt{3} $)	Равно линейному ($ U_{ph} = U_L $)
Линейный ток	Равен фазному ($ I_L = I_{ph} $)	В $ \sqrt{3} $ раз больше фазного ($ I_L = \sqrt{3} I_{ph} $)
Нулевой провод	Возможен (для несимметрии)	Не используется конструктивно
Основное применение	Двигатели (мягкий пуск), освещение	Двигатели (номинальный режим), мощные нагреватели

Преимущества и недостатки схем

Звезда:

(+) Возможность получить два напряжения (фазное 220В и линейное 380В).
(+) Меньшая нагрузка на изоляцию обмоток (напряжение ниже).
(-) При обрыве нуля (в несимметричной схеме) возможен перекос фаз.

Треугольник:

(+) Максимальная мощность двигателя.
(+) Схема более устойчива к несимметрии нагрузки (нет смещения нейтрали, так как нет самой нейтрали).
(-) Сложнее реализовать защитное заземление (требуется искусственная нейтраль).

5. Интересные факты о трехфазных цепях

Экономия меди: Трехфазная система расходует на 25% меньше металла проводов по сравнению с однофазной для передачи той же мощности.
Магия числа 3: Три фазы — это минимальное число фаз, позволяющее создать вращающееся магнитное поле без дополнительных устройств (конденсаторов).
Корень из трех: Число $ 1.73 $ (корень из 3) является «священным» для электриков, связывая фазные и линейные величины.
Никола Тесла: Хотя Тесла экспериментировал с многофазными токами, именно Доливо-Добровольский оптимизировал систему до 3-х фаз, в то время как Тесла склонялся к двум.
Обратимость: Асинхронный двигатель в трехфазной сети может легко стать генератором, если его раскрутить выше синхронной скорости (рекуперация).
120 градусов: Сдвиг фаз выбран не случайно — это деление круга (360°) на 3 равные части для равномерности вращения.
Универсальность: Почти вся электроэнергия в мире генерируется и передается в трехфазном виде.

6. FAQ: Часто задаваемые вопросы

1. Почему в примере ток нуля равен нулю?

Потому что нагрузка симметрична. Векторная сумма трех одинаковых токов, сдвинутых на 120 градусов, всегда дает ноль. Это как три человека, тянущие кольцо в разные стороны с одинаковой силой.

2. Можно ли подключить двигатель 380/220В треугольником в сеть 380В?

В сеть с линейным напряжением 380В такой двигатель нужно включать звездой. Если включить треугольником, на обмотку, рассчитанную на 220В, пойдет 380В, и она сгорит. Треугольник для такого двигателя возможен только в сети 220В (линейное).

3. Что будет, если перепутать фазы?

Для активной нагрузки (нагреватель) — ничего. Для двигателя изменится порядок чередования фаз, и он начнет вращаться в обратную сторону.

4. Что такое линейное и фазное напряжение простыми словами?

Линейное — это напряжение между двумя «горячими» проводами (фазами А и В). Фазное — это напряжение между одним «горячим» проводом и «землей» (нулем). В квартире у вас фазное (220В), а в щитке в подъезде есть линейное (380В).

5. Зачем нужен MathJax в этой статье?

Он позволяет отображать векторные величины (например, $ \dot{I} $) и комплексные числа корректно, что критически важно для понимания фазовых сдвигов, которые нельзя показать обычным текстом.

Заключение

Понимание симметричных режимов работы цепи является базой для расчета любых электротехнических устройств. Несмотря на то, что в реальности идеальная симметрия встречается редко, расчет по методу симметричных составляющих базируется именно на этих принципах. Знание различий между «звездой» и «треугольником» позволяет грамотно выбирать оборудование и избегать аварийных режимов.

Нормативная база и литература

ГОСТ 29322-2014 (IEC 60038:2009) — Напряжения стандартные.
ГОСТ 32144-2013 — Нормы качества электрической энергии в системах электроснабжения.
ГОСТ 2.702-2011 — ЕСКД. Правила выполнения электрических схем.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи.