Резонанс напряжений: физика процесса, условие возникновения, теория и расчет

Содержание страницы

1. Условия возникновения резонанса напряжений
2. Токи и напряжения в цепи
3. Частотные характеристики и добротность
4. Практический пример расчета
5. Понимание явления
6. Сравнение: Резонанс напряжений vs Резонанс токов
7. Преимущества и недостатки явления резонанса
8. Интересные факты о резонансе
9. Часто задаваемые вопросы (FAQ)
Заключение

Резонанс напряжений — это особое состояние электрической цепи переменного тока, содержащей последовательно соединенные индуктивность и емкость, при котором индуктивное и емкостное сопротивления становятся равными. В этот момент ток в цепи достигает максимума, а напряжения на катушке и конденсаторе могут многократно превышать напряжение источника питания.

Краткая история: Явление электрического резонанса было теоретически предсказано лордом Кельвином в 1853 году и экспериментально подтверждено Генрихом Герцем в 1887 году при опытах с вибратором (предшественником антенны), что стало фундаментом для всей современной радиотехники.

1. Условия возникновения резонанса напряжений

Резонанс напряжений, или последовательный резонанс, может возникнуть в последовательном контуре цепи, состоящей из последовательного соединения элементов \( R \), \( L \) и \( C \) (см. рис. 1).

Реактивное сопротивление такой цепи определяется разностью индуктивного и емкостного сопротивлений:

X = \omega L — \frac{1}{\omega C}

Так как по определению при резонансе полное реактивное сопротивление равно нулю (\( X = 0 \)), то условием возникновения резонанса является равенство:

\omega L = \frac{1}{\omega C}

Добиться возникновения резонанса можно двумя путями:

Изменяя частоту питающего цепь синусоидального напряжения.
Изменяя параметры элементов \( C \) (емкость) и \( L \) (индуктивность) при фиксированной частоте.

Резонансные частоты и параметры

При постоянных значениях индуктивности \( L \) и емкости \( C \) резонансная угловая частота \( \omega_p \) определяется формулой (формула Томсона):

\omega_p = \frac{1}{\sqrt{LC}}

Если частота источника задана, то резонанса можно достичь подбором компонентов:

При постоянных частоте и емкости \( C \) резонансное значение индуктивности: \( L_p = \frac{1}{\omega^2 C} \).
При постоянных частоте и индуктивности \( L \) резонансная емкость: \( C_p = \frac{1}{\omega^2 L} \).

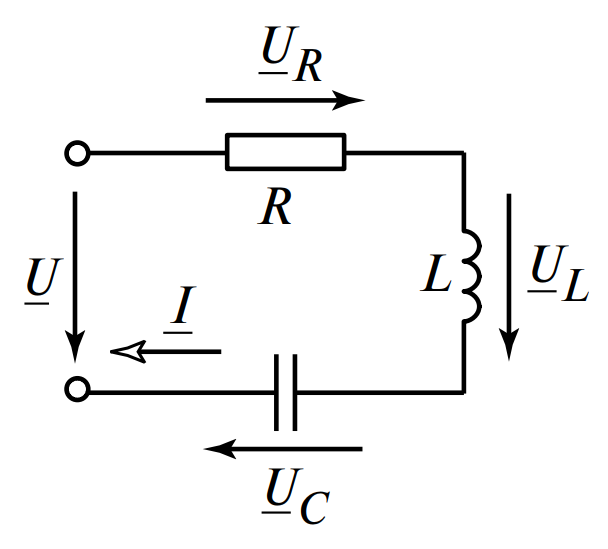
Схема последовательного RLC-контура с источником переменного напряжения

На схеме изображены последовательно соединенные резистор R, катушка индуктивности L и конденсатор C, подключенные к источнику напряжения U.

Рис. 1. Последовательный RLC-контур

2. Токи и напряжения в цепи

Ранее в курсе электротехники было получено выражение для действующего значения тока в последовательно соединенных элементах \( R \), \( L \) и \( C \) (закон Ома для цепи переменного тока):

I = \frac{U}{\sqrt{R^2 + \left(\omega L — \frac{1}{\omega C}\right)^2}}

При наступлении резонанса, когда \( \omega L — \frac{1}{\omega C} = 0 \), полное сопротивление цепи становится чисто активным и минимально возможным (\( Z = R \)). Следовательно, резонансное значение тока \( I_p \) достигает максимума:

I_p = \frac{U}{R}

Действующие значения напряжений на реактивных элементах определяются по формулам:

U_L = I \cdot \omega L $$ $$ U_C = I \cdot \frac{1}{\omega C}

Поскольку при резонансе \( \omega L = \frac{1}{\omega C} \), то и напряжения на этих элементах равны по модулю: \( U_L = U_C \). Однако они находятся в противофазе и компенсируют друг друга в общем балансе напряжений цепи.

Важное замечание: Напряжения \( U_L \) и \( U_C \) могут быть значительно больше напряжения источника питания. Это явление и дало название «резонанс напряжений».

3. Частотные характеристики и добротность

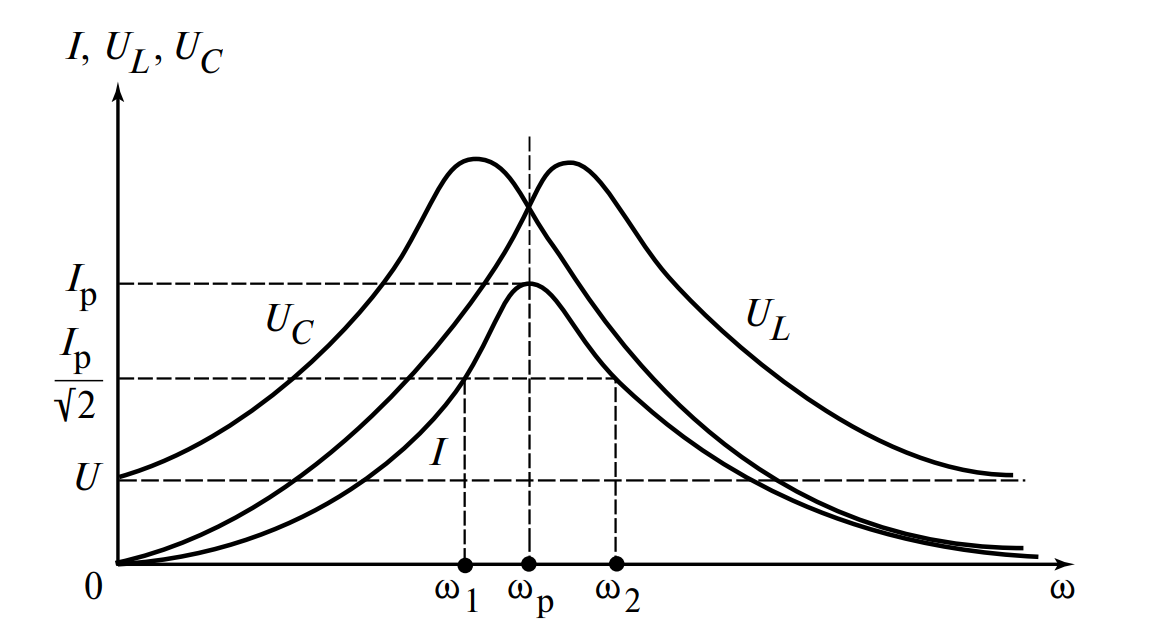
Рассмотрим поведение цепи при изменении частоты. Разность частот \( \omega_1 \) и \( \omega_2 \), соответствующих токам в \( \sqrt{2} \) раз меньшим, чем резонансный ток \( I_p \), дает полосу пропускания последовательного контура:

\Delta\omega = \omega_2 — \omega_1

Важнейшей характеристикой контура является добротность (\( Q \)). Она определяется как отношение резонансной частоты к полосе пропускания:

Q = \frac{\omega_p}{\Delta\omega}

С физической точки зрения, при резонансе в последовательном контуре напряжения на реактивных элементах в \( Q \) раз больше, чем напряжение источника питания:

U_{L_p} = U_{C_p} = Q \cdot U

Добротность также может быть рассчитана через параметры элементов контура:

Q = \frac{\rho}{R}

где \( \rho = \sqrt{\frac{L}{C}} \) — характеристическое (волновое) сопротивление контура.

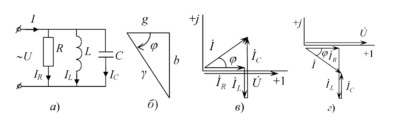
Рис. 2. Частотные характеристики последовательного RLC-контура

Векторная диаграмма

При резонансе напряжений вектор тока совпадает по фазе с вектором напряжения источника. Напряжения на индуктивности и емкости равны по величине и направлены в противоположные стороны, взаимно уничтожаясь.

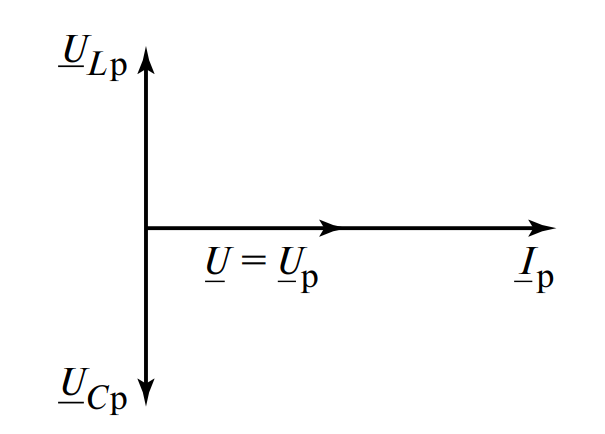
Рис. 3. Векторная диаграмма при резонансе напряжений

4. Практический пример расчета

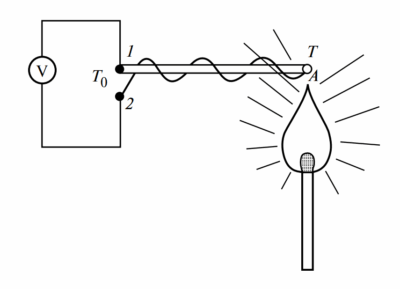
Пример 1. Дано: реальная катушка (реактор), обладающая индуктивностью \( L \) и активным сопротивлением \( R \), последовательно соединена с конденсатором емкостью \( C \). Действующие значения напряжений на входе цепи и на конденсаторе известны:

Напряжение источника: \( U = 60 \) В
Напряжение на конденсаторе: \( U_C = 80 \) В

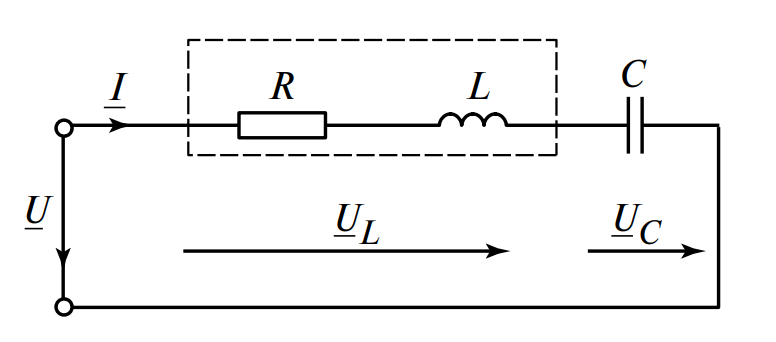
Схема представлена на рис. 4.

Задача: Найти напряжение на реакторе \( U_p \) (напряжение на зажимах реальной катушки), если в цепи имеет место резонанс напряжений. Построить векторную диаграмму напряжений на комплексной плоскости.

Рис. 4. Схема к примеру 1

Решение:

1. Анализ фаз. Из условия резонанса напряжений следует, что комплексный ток совпадает по фазе с комплексом напряжения на входе цепи (так как реактивное сопротивление всей цепи равно нулю).

2. Векторные соотношения. Напряжение на емкости отстает от тока на 90°. По второму закону Кирхгофа сумма векторов напряжений на элементах равна напряжению источника:

\vec{U} = \vec{U}_p + \vec{U}_C

Где \( \vec{U}_p \) — вектор напряжения на реальной катушке (включающей \( R \) и \( L \)).

3. Расчет.
При резонансе напряжение на идеальной индуктивности \( U_L \) компенсирует напряжение на емкости \( U_C \), то есть \( U_L = U_C = 80 \) В.
Однако напряжение на всем реакторе \( U_p \) складывается из напряжения на его активном сопротивлении \( U_R \) и напряжения на индуктивности \( U_L \).
Поскольку при резонансе все напряжение источника прикладывается к активному сопротивлению, то \( U_R = U = 60 \) В.

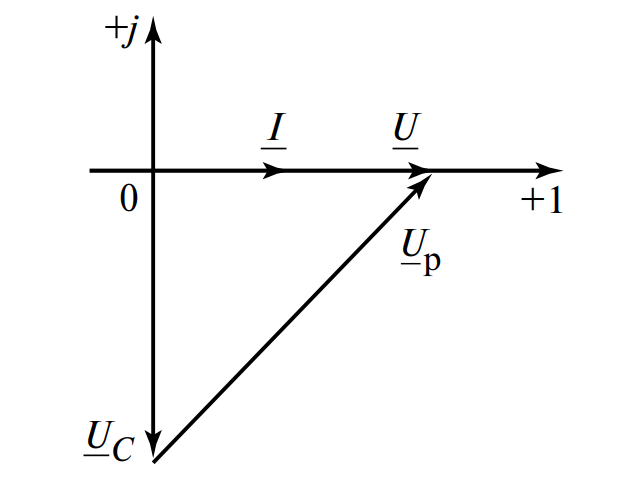
Векторная диаграмма представляет собой прямоугольный треугольник (см. рис. 5), где гипотенузой является искомое напряжение на реакторе \( U_p \), а катетами — напряжение источника \( U \) (оно же \( U_R \)) и напряжение на индуктивной части (равное \( U_C \)).

Из векторной диаграммы (по теореме Пифагора) находим модуль напряжения реактора:

U_p = \sqrt{U^2 + U_C^2}

U_p = \sqrt{60^2 + 80^2} = \sqrt{3600 + 6400} = \sqrt{10000} = 100 \text{ В}

Рис. 5. Векторная диаграмма к примеру 1

5. Понимание явления

Аналогия для понимания

Представьте себе качели. Если вы будете подталкивать их ровно в тот момент, когда они начинают движение вниз (в такт с их собственной частотой колебаний), то даже слабыми толчками вы сможете раскачать их очень сильно.

Толчки — это напряжение источника \( U \).
Размах качелей — это напряжение на конденсаторе и катушке (\( U_C, U_L \)).
Трение в подшипниках — это активное сопротивление \( R \).

При резонансе «размах» (напряжение на элементах) может быть огромным, даже если «толчки» (питающее напряжение) слабые. Чем меньше трение (\( R \)), тем выше добротность и сильнее раскачка.

6. Сравнение: Резонанс напряжений vs Резонанс токов

Параметр	Резонанс напряжений	Резонанс токов
Тип соединения	Последовательное (R, L, C)	Параллельное (L \|\| C)
Что возрастает?	Напряжения на L и C (\( U_L, U_C > U \))	Токи в ветвях L и C (\( I_L, I_C > I \))
Сопротивление цепи	Минимальное (\( Z = R \))	Максимальное (стремится к \( \infty \) в идеальном контуре)
Ток от источника	Максимальный (\( I = U/R \))	Минимальный (компенсация реактивных токов)
Опасность	Пробой изоляции конденсатора или катушки	Перегрев проводов внутри контура из-за больших токов

7. Преимущества и недостатки явления резонанса

Преимущества (Где это полезно):

Радиотехника: Используется во входных цепях радиоприемников для настройки на нужную волну (выделение сигнала конкретной частоты из множества помех).
Фильтрация: Создание полосовых фильтров.
Энергетика: В некоторых схемах для повышения напряжения без трансформаторов.

Недостатки (Где это опасно):

Электрические сети: Случайный резонанс в кабельных линиях может вызвать перенапряжения, приводящие к пробою изоляции (аварии).
Измерительные приборы: Может вывести из строя вольтметры или конденсаторы, не рассчитанные на высокое напряжение добротности.

8. Интересные факты о резонансе

Экстремальное усиление. Напряжение на конденсаторе при резонансе может быть в 10-100 раз выше напряжения в розетке, если сопротивление проводов мало.
Универсальность физики. Понятие резонанса универсально: разрушение мостов от ветра или стакана от голоса оперного певца имеет ту же физическую природу, что и резонанс в RLC-цепи.
Борьба в энергетике. В системах высоковольтной передачи энергии специально борются с резонансом, устанавливая демпфирующие реакторы.
Рекордная добротность. Добротность \( Q \) обычного радиолюбительского контура составляет 50–200, а кварцевого резонатора может достигать 1 000 000.
Звуковые корни. Явление впервые описано в работах по теории звука, и лишь позже перенесено на электричество.
Парадокс бесконечности. Если \( R=0 \) (сверхпроводимость), то при резонансе ток и напряжения стремились бы к бесконечности.
RFID и технологии. Технология RFID-меток (в магазинах и пропусках) работает на принципе резонанса: метка получает энергию от считывателя, когда их частоты совпадают.

9. Часто задаваемые вопросы (FAQ)

1. Почему сопротивление при резонансе напряжений минимально?

Потому что реактивные сопротивления катушки и конденсатора имеют разные знаки. При резонансе они равны по модулю и вычитаются друг из друга (\( X_L — X_C = 0 \)). Остается только активное сопротивление проводов \( R \).

2. Может ли возникнуть резонанс, если в цепи нет конденсатора?

Нет. Для резонанса необходим обмен энергией между магнитным полем (индуктивность) и электрическим полем (емкость). Если одного из элементов нет, колебательный процесс невозможен.

3. Как изменится резонансная частота, если увеличить индуктивность в 4 раза?

Согласно формуле \( \omega_p = 1/\sqrt{LC} \), при увеличении \( L \) в 4 раза знаменатель увеличится в \( \sqrt{4} = 2 \) раза. Значит, частота уменьшится в 2 раза.

4. Что такое полоса пропускания простыми словами?

Это диапазон частот вокруг резонансной, в котором ток в цепи остается достаточно сильным (не менее 70.7% от максимума). Чем уже полоса, тем «избирательнее» приемник.

5. Опасно ли включать RLC-цепь в розетку?

Если параметры \( L \) и \( C \) случайно совпадут с частотой сети (50 Гц), возникнет резонанс. Ток резко возрастет (короткое замыкание), а напряжение на конденсаторе может взорвать его. Это очень опасно без предварительных расчетов.

Заключение

Резонанс напряжений — это фундаментальное явление в цепях переменного тока, характеризующееся взаимной компенсацией реактивных сопротивлений. Понимание этого процесса критически важно как для инженеров-связистов (для настройки частот), так и для энергетиков (для предотвращения аварий). Мы рассмотрели условия возникновения, векторные диаграммы и расчетные формулы, которые позволят вам успешно решать задачи по ТОЭ и применять знания на практике.

Нормативная база и литература

При проектировании и расчетах электрических цепей следует руководствоваться действующими стандартами:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий».
ГОСТ 19880-74 «Электротехника. Основные понятия. Термины и определения».
Бессонов Л.А. «Теоретические основы электротехники. Электрические цепи» — классический учебник для вузов.