Резистор в электротехнике: устройство, характеристики, теория и расчет

Содержание страницы

1. Физическая природа и принцип действия
2. Математическая модель резистивного элемента
3. Установившийся синусоидальный режим (AC Analysis)
4. Мощность резистора
5. Практический пример: Полный расчет резистора для светодиода
6. Разбор компонентов и выбор элементной базы
7. Интересные факты о резисторах и сопротивлении
8. Часто задаваемые вопросы (FAQ)

Резистор — это пассивный элемент электрической цепи, обладающий определенным или переменным значением электрического сопротивления, предназначенный для линейного преобразования силы тока в напряжение и напряжения в силу тока, а также для ограничения тока и поглощения электрической энергии. Это фундаментальный «кирпич» любой электронной схемы, от простейшего фонарика до суперкомпьютера. В отличие от реактивных компонентов (конденсаторов и катушек индуктивности), резистор не накапливает энергию в электрическом или магнитном поле, а безвозвратно рассеивает её.

Историческая справка: Открытие сопротивления

Понятие электрического сопротивления и фундаментальный закон, связывающий ток и напряжение, были открыты немецким физиком Георгом Симоном Омом в 1826 году. В то время это было революционным открытием. Ом проводил эксперименты, используя гальванические батареи и проводники различной длины и толщины. Интересно, что научное сообщество того времени встретило его труды с холодом и даже враждебностью, считая подход «слишком математическим» для физики. Только спустя десятилетия закон Ома был признан базовым законом электродинамики, а единица измерения сопротивления (Ом) была названа в его честь в 1881 году.

1. Физическая природа и принцип действия

В основе работы резистора лежит физический процесс рассеяния носителей заряда (электронов в металлах) на неоднородностях кристаллической решетки проводника. Когда электрическое поле ускоряет электроны, они приобретают кинетическую энергию. Сталкиваясь с ионами решетки, электроны передают им часть своей энергии, что приводит к увеличению амплитуды колебаний ионов. Макроскопически это проявляется как нагрев проводника.

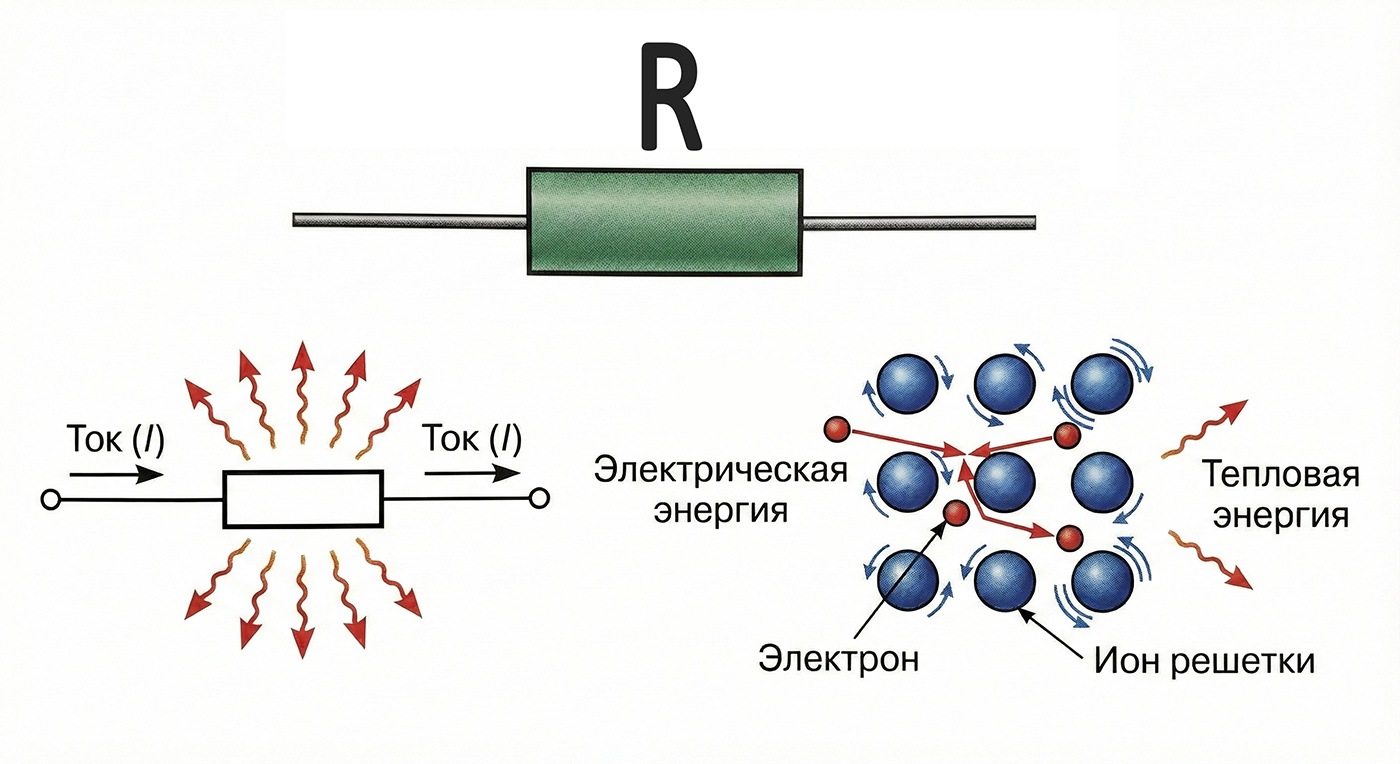
Рис. 1. Резистор и физический процесс его нагрева. Схематическое изображение процесса рассеяния электронов.

Этот процесс является необратимым преобразованием электрической энергии в тепловую (диссипация). В частных случаях, в зависимости от конструкции и назначения, энергия может преобразовываться в механическую (пьезорезисторы) или химическую, но в контексте классической электротехники мы говорим именно о тепле.

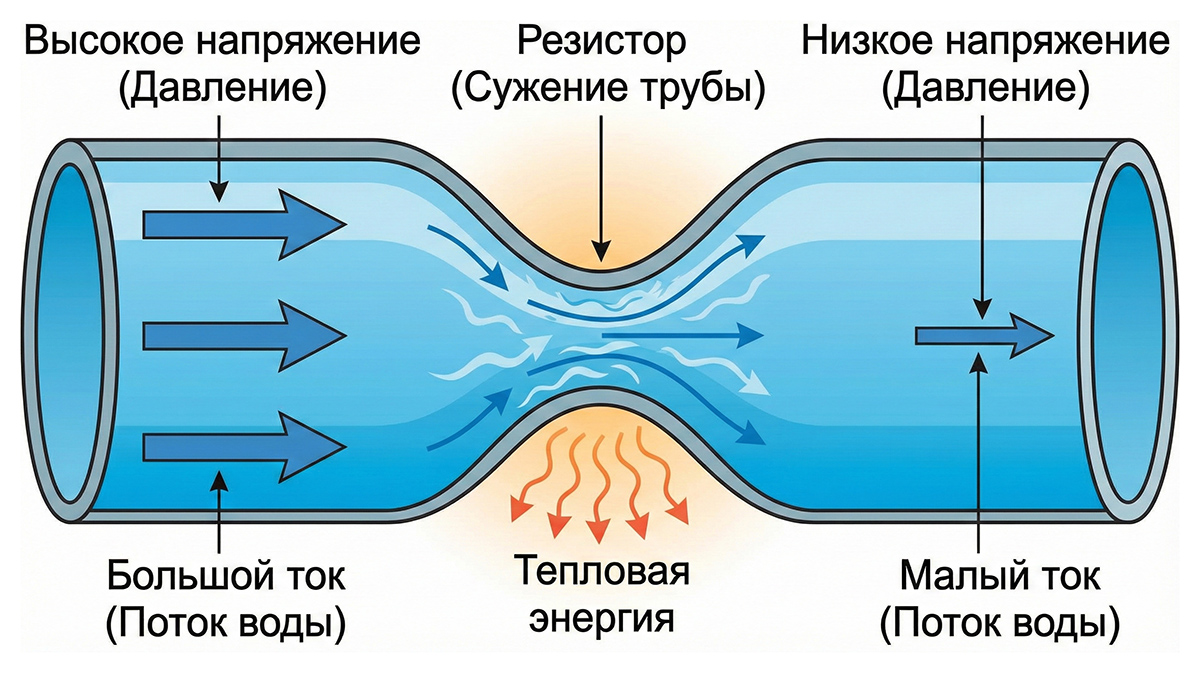
Аналогия: Гидравлическая система

Представьте электрический ток как поток воды в трубе. Напряжение — это давление воды, а резистор — это участок трубы, забитый песком или губкой. Воде (электронам) трудно просачиваться сквозь препятствие. Трение воды о песок (сопротивление) заставляет воду терять напор (падение напряжения) и нагревать песок (выделение тепла). Чем плотнее песок или чем длиннее этот участок, тем выше сопротивление и тем меньше воды протечет при том же давлении.

2. Математическая модель резистивного элемента

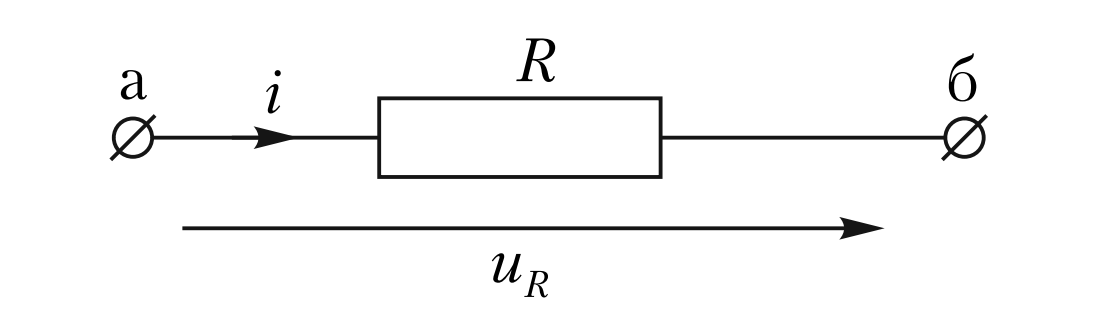
Рассмотрим схему замещения, где резистор представлен как идеализированный элемент. При выбранных положительных направлениях (см. Рис. 2) ток и напряжение на резисторе связаны фундаментальным соотношением, вытекающим из закона Ома для участка цепи.

Рис. 2. Резистор — элемент, необратимо преобразующий электрическую энергию в тепловую.

Базовые уравнения

Напряжение на резисторе $ u_R $ определяется разностью потенциалов между его выводами (точками подключения «а» и «б»):

$$ u_R = u_{ab} = \phi_a — \phi_b = i \cdot R $$

Где:

$ \phi_a, \phi_b $ — электрические потенциалы точек «а» и «б» соответственно (измеряются в Вольтах, В). Потенциал характеризует потенциальную энергию единичного заряда в данной точке поля.
$ i $ — мгновенное значение тока, протекающего через резистор (Амперы, А).
$ R $ — электрическое сопротивление резистора (Омы, Ом).

Понятие линейности

Если величина сопротивления $ R = \text{const} $, то есть она является константой и не зависит от:

Величины протекающего тока;
Приложенного напряжения;
Времени протекания тока;

То такой резистор называется линейным. В линейных электрических цепях выполняется принцип суперпозиции, что значительно упрощает расчеты.

Для линейного резистора связь между мгновенными значениями напряжения и тока описывается линейным алгебраическим уравнением:

$$ u_R(t) = R \cdot i(t) $$

Это уравнение (обозначим его как формула 1) говорит нам о том, что форма кривой напряжения полностью повторяет форму кривой тока, отличаясь только масштабом (множителем $ R $). Если ток постоянный (DC), то и напряжение постоянно. Если ток — треугольный импульс, напряжение будет иметь форму треугольника.

Важно: В реальности абсолютно линейных резисторов не существует. При сильном нагреве сопротивление меняется (температурный коэффициент сопротивления), а при сверхвысоких напряжениях может возникать нелинейность из-за пробоя микроструктур. Однако в рабочих диапазонах мы принимаем допущение $ R = \text{const} $.

3. Установившийся синусоидальный режим (AC Analysis)

Наибольший интерес для электроэнергетики и радиотехники представляет поведение резистора в цепях переменного гармонического (синусоидального) тока. Рассмотрим случай, когда ток изменяется по периодическому закону.

Математическое описание тока

Пусть ток в цепи описывается функцией времени:

$$ i(t) = I_m \sin(\omega t + \psi) $$

Разбор компонентов формулы:

$ I_m $ — Амплитуда тока (максимальное значение). Единица: Ампер.
$ \omega t + \psi $ — Полная фаза колебаний.
$ \psi $ — Начальная фаза (значение фазы при $ t=0 $). На Рис. 2 для упрощения принято $ \psi = 0 $.
$ \omega $ — Угловая частота, показывающая скорость изменения фазы. Связана с периодом $ T $ и частотой $ f $ соотношением:
$$ \omega = 2\pi f = \frac{2\pi}{T} $$
$ T $ — Период синусоиды (время одного полного колебания).

Вывод уравнения напряжения

Подставим выражение для тока в основное уравнение линейного резистора (формула 1):

$$ u_R(t) = R \cdot i(t) = R \cdot [I_m \sin(\omega t + \psi)] $$

Используя ассоциативность умножения, сгруппируем константы:

$$ u_R(t) = (R \cdot I_m) \sin(\omega t + \psi) $$

Обозначим произведение $ R \cdot I_m $ как амплитуду напряжения $ U_{mR} $. Тогда получаем финальное уравнение:

$$ u_R(t) = U_{mR} \sin(\omega t + \psi) $$

Рис. 3. Графики мгновенных значений тока и напряжения. В синусоидальном режиме напряжение и ток в резисторе совпадают по фазе.

Физический смысл результата

Из полученного вывода следуют два критически важных заключения для инженеров:

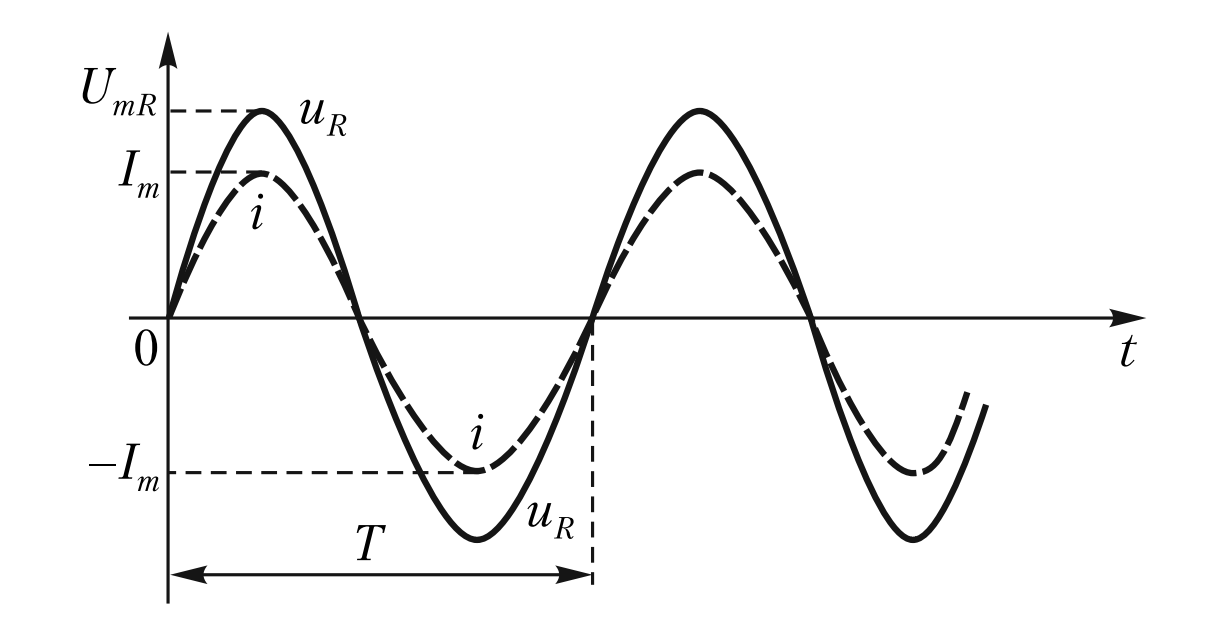
1. Совпадение по фазе: Аргумент синуса $ (\omega t + \psi) $ одинаков и для тока, и для напряжения.

Это означает, что фазовый сдвиг $ \varphi $ между ними равен нулю:

$$ \varphi = \psi_u — \psi_i = 0 $$

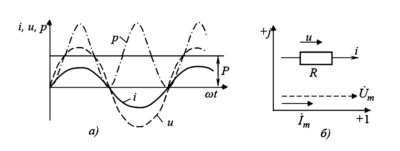
Визуально (см. Рис. 3) это значит, что график напряжения и график тока одновременно пересекают ось времени (нулевое значение) и одновременно достигают своих максимумов и минимумов.

Резистор — это активное сопротивление, он не вносит инерции в систему.

2. Закон Ома для амплитуд: Амплитуды связаны простейшим линейным соотношением:

$$ U_{mR} = R \cdot I_m $$

Это соотношение справедливо и для действующих (среднеквадратичных) значений: $ U = I \cdot R $, где $ U = U_m/\sqrt{2} $.

4. Мощность резистора

Мгновенная мощность, поступающая в резистор, определяется произведением мгновенных значений напряжения и тока:

$$ p(t) = u_R(t) \cdot i(t) $$

Для синусоидального режима, учитывая совпадение фаз:

$$ p(t) = U_m \sin(\omega t) \cdot I_m \sin(\omega t) = U_m I_m \sin^2(\omega t) $$

Используя тригонометрическую формулу понижения степени $ \sin^2\alpha = \frac{1 — \cos 2\alpha}{2} $, получаем:

$$ p(t) = \frac{U_m I_m}{2} (1 — \cos 2\omega t) $$

Вывод: Мгновенная мощность пульсирует с двойной частотой $ 2\omega $ относительно частоты тока. При этом график мощности всегда находится в положительной области (выше нуля). Это математически подтверждает, что резистор всегда потребляет энергию, никогда не возвращая её обратно в источник. Среднее значение этой мощности за период называется активной мощностью $ P $:

$$ P = \frac{U_m I_m}{2} = \frac{U_m}{\sqrt{2}} \cdot \frac{I_m}{\sqrt{2}} = U \cdot I = I^2 R $$

5. Практический пример: Полный расчет резистора для светодиода

Самая частая задача — расчет токоограничивающего резистора. Светодиод (LED) — это нелинейный элемент, и если подключить его к источнику напряжения напрямую, он сгорит практически мгновенно из-за лавинообразного роста тока. Резистор в этой цепи выступает в роли «узкого горлышка», ограничивающего ток на безопасном уровне.

Рассмотрим классическую задачу: нужно подключить стандартный красный светодиод к бортовой сети автомобиля (12 Вольт).

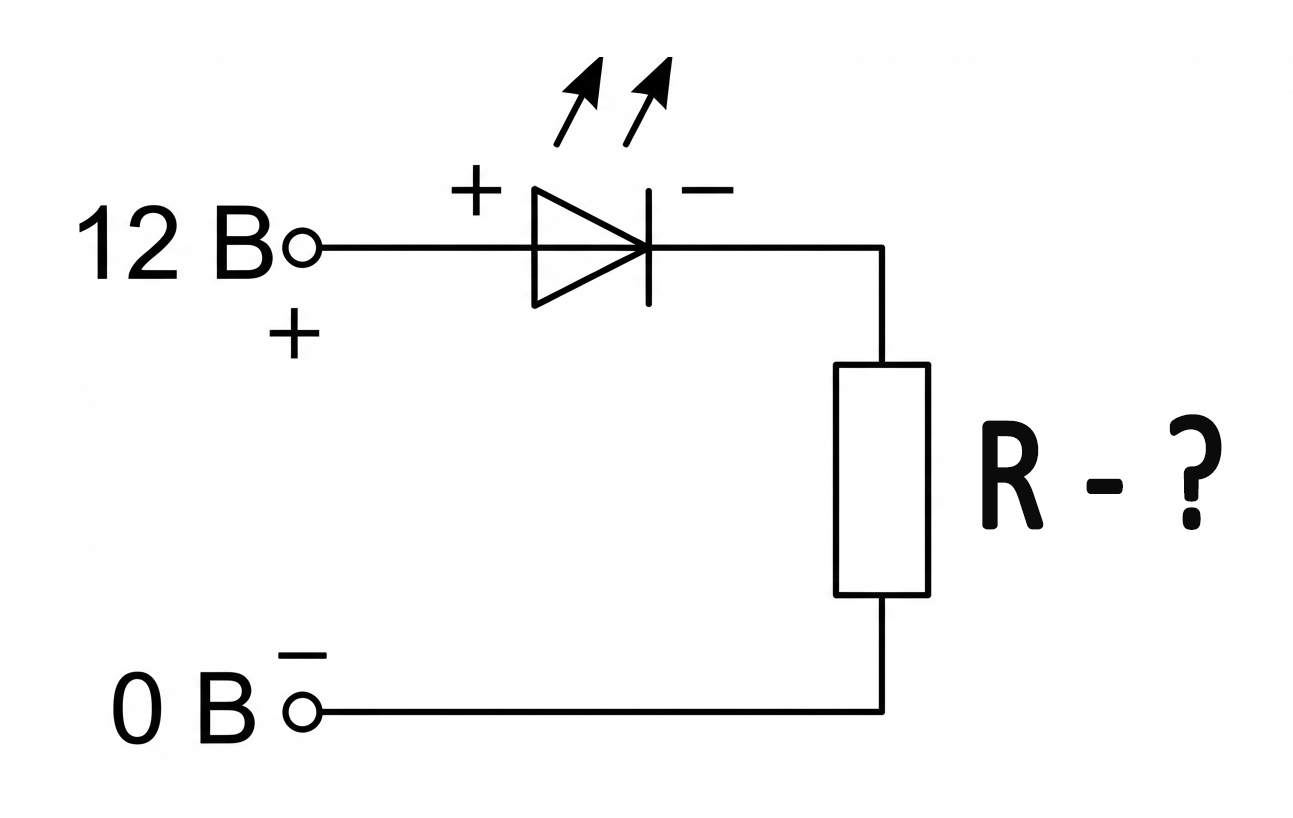
Рис. 4. Схема подключения светодиода через токоограничивающий резистор.

Дано:

Напряжение источника питания ($ U_{pit} $): 12 В (Вольт).
Прямое падение напряжения на светодиоде ($ U_{led} $): Для обычного красного светодиода это справочная величина, обычно составляющая около 2.0 В.
Рабочий ток светодиода ($ I_{rab} $): Типовое значение для индикаторных светодиодов — 20 мА (миллиампер). Для расчетов переводим в Амперы: $ 0.02 \, \text{А} $.

Шаг 1: Расчет падения напряжения на резисторе

Согласно второму закону Кирхгофа, сумма напряжений на элементах последовательной цепи равна напряжению источника. Резистор должен погасить «лишнее» напряжение, которое не нужно светодиоду.

$$ U_R = U_{pit} — U_{led} $$

Подставляем значения:

$$ U_R = 12 \, \text{В} — 2 \, \text{В} = 10 \, \text{В} $$

Вывод: Резистор должен взять на себя 10 Вольт и рассеять их в виде тепла.

Шаг 2: Расчет сопротивления (Закон Ома)

Теперь, зная напряжение на резисторе и ток, который должен через него протекать (тот же, что и через светодиод, так как цепь последовательная), применяем закон Ома:

$$ R = \frac{U_R}{I_{rab}} $$

$$ R = \frac{10 \, \text{В}}{0.02 \, \text{А}} = 500 \, \text{Ом} $$

Шаг 3: Выбор номинала из стандартного ряда (E24)

Если вы посмотрите в таблицу стандартных значений резисторов (ряд E24), вы увидите, что резистора ровно на 500 Ом не существует. Ближайшие значения:

470 Ом (Ток будет чуть больше: $ I = 10/470 \approx 21.2 \, \text{мА} $).
510 Ом (Ток будет чуть меньше: $ I = 10/510 \approx 19.6 \, \text{мА} $).

Совет

В электронике хорошим тоном считается выбирать номинал в большую сторону (ближайшее большее значение — 510 Ом). Незначительное снижение тока (на 0.4 мА) глаз не заметит, зато это продлит жизнь светодиоду («бережный режим») и снизит нагрев.

Итак, предварительно выбираем $ R = 510 \, \text{Ом} $.

Шаг 4: Расчет мощности и выбор корпуса

Это критический этап, который новички часто пропускают, из-за чего резисторы чернеют и пахнут гарью. Нам нужно узнать, сколько тепла выделится на корпусе резистора.

Формула мощности:

$$ P = U_R \cdot I_{rab} $$

или

$$ P = I_{rab}^2 \cdot R $$

Используем первый вариант (он проще для расчетов в уме):

$$ P = 10 \, \text{В} \cdot 0.02 \, \text{А} = 0.2 \, \text{Вт (Ватт)} $$

Анализ результата:

Стандартные выводные резисторы имеют мощностные ряды: 0.125 Вт, 0.25 Вт, 0.5 Вт, 1 Вт и т.д.

0.125 Вт: Слишком мало ($ 0.125 < 0.2 $), резистор сгорит мгновенно.
0.25 Вт: Формально подходит ($ 0.25 > 0.2 $), но запас слишком мал. Резистор будет работать на 80% от предела своих возможностей, будет очень горячим (>70°C), что со временем может повредить плату.
0.5 Вт: Идеальный вариант. Запас по мощности более чем двукратный. Резистор будет чуть теплым.

Итог: Для надежного подключения светодиода к 12 В нам необходим резистор сопротивлением 510 Ом и мощностью рассеяния не менее 0.5 Вт.

6. Разбор компонентов и выбор элементной базы

При проектировании реальных устройств недостаточно знать формулу $ U=IR $. Необходимо правильно выбрать тип компонента.

Сравнительная таблица технологий резисторов

Тип резистора	Материал	Преимущества	Недостатки	Область применения
Углеродистые (Carbon Film)	Пленка углерода на керамике	Дешевизна, доступность, высокая импульсная стойкость.	Высокий уровень шумов, низкая точность, дрейф от температуры.	Бытовая электроника, неответственные цепи.
Металлопленочные (Metal Film)	Тонкий слой металла	Низкий шум, высокая точность (до 0.1%), стабильность.	Меньшая стойкость к импульсным перегрузкам по сравнению с проволочными.	Аудиоаппаратура, измерительные приборы, точная электроника.
Проволочные (Wirewound)	Проволока (манганин, константан)	Огромная рассеиваемая мощность, высочайшая точность, термостабильность.	Имеют паразитную индуктивность (работают как катушка), большие габариты.	Силовые цепи, шунты тока, прецизионные делители.

Критические параметры при выборе

Номинальная мощность рассеяния $ (P_{nom}) $: Самый важный параметр после сопротивления. Если мощность, выделяемая на резисторе $ (P = I^2R) $, превысит номинальную, резистор перегреется и сгорит.
ТКС (Температурный коэффициент сопротивления): Показывает, насколько изменится сопротивление при нагреве на 1 градус. Для точных приборов нужен минимальный ТКС.
Предельное рабочее напряжение: Даже если мощность не превышена, высокое напряжение может вызвать электрический пробой по поверхности корпуса.

7. Интересные факты о резисторах и сопротивлении

Мир пассивных компонентов гораздо увлекательнее, чем кажется на первый взгляд. Вот 7 фактов, которые расширят ваше инженерное понимание:

Глобальный стандарт E. Вы когда-нибудь задумывались, почему существуют резисторы на 4.7 кОм, но нет ровно на 5 кОм? Это связано с рядами предпочтительных чисел (ряды E6, E12, E24 и т.д.), разработанными еще в начале 20 века. Значения в них распределены по логарифмическому закону, чтобы перекрывать весь диапазон сопротивлений с учетом погрешности (допуска). Это гениальная математическая оптимизация производства.
Шум Джонсона — Найквиста. Даже если резистор просто лежит на столе и никуда не подключен, внутри него генерируется электрический шум. Хаотичное тепловое движение электронов создает флуктуации напряжения на выводах. Чем выше температура и сопротивление, тем сильнее этот «белый шум». Это физическое ограничение чувствительности любого приемника во Вселенной.
Самый мощный резистор. В электровозах и трамваях используются гигантские тормозные реостаты. При торможении двигатели переключаются в режим генераторов, и вся кинетическая энергия многотонного поезда превращается в электричество, которое сжигается на огромных резисторах на крыше, нагревая атмосферу. Это наглядная демонстрация закона сохранения энергии.
Отрицательное сопротивление. Существуют экзотические приборы (например, туннельные диоды), которые на определенном участке вольт-амперной характеристики ведут себя вопреки закону Ома: при увеличении напряжения ток через них уменьшается. Это явление называют дифференциальным отрицательным сопротивлением, и оно используется для создания генераторов частоты.
Человек-резистор. Сопротивление сухой кожи человека может достигать 100 кОм, но стоит коже вспотеть или получить повреждение, как оно падает до 1 кОм и ниже. Именно поэтому низкие напряжения (до 40-50 В) считаются условно безопасными в сухих помещениях, но смертельно опасными во влажных. Полиграфы (детекторы лжи) работают именно на измерении изменения сопротивления кожи (КГР).
Нулевой предел. При охлаждении некоторых материалов (ртуть, свинец, ниобий) до температур, близких к абсолютному нулю, их электрическое сопротивление исчезает полностью. Ток в замкнутом кольце сверхпроводника может циркулировать годами без затухания. Это единственное исключение из правила, что «резистор всегда греется».
Лазерная подгонка. Внутри прецизионных микросхем резисторы создаются методом напыления. Чтобы добиться точности в 0.01%, на заводе специальный лазер выжигает часть проводящего слоя (делает L-образный надрез), физически удлиняя путь тока и повышая сопротивление до идеального значения уже после сборки кристалла.

8. Часто задаваемые вопросы (FAQ)

Есть ли у резистора полярность (плюс и минус)?

Нет, резистор — это симметричный компонент. Ему абсолютно все равно, в какую сторону течет ток. Вы можете смело переворачивать его в схеме на 180 градусов, работа устройства не изменится. Это отличает его от диодов или электролитических конденсаторов.

Почему резистор греется и нормально ли это?

Да, нагрев — это его основная функция с точки зрения физики. Согласно закону Джоуля-Ленца, энергия электрического поля преобразуется в тепло при столкновении электронов с решеткой материала. Если резистор теплый — он работает. Если он дымит или чернеет — превышена допустимая мощность рассеяния, и его нужно заменить на более мощный аналог.

Можно ли ставить резистор большей мощности, чем указано в схеме?

Да, безусловно. Если в схеме указан резистор 0.25 Вт, вы можете поставить 0.5 Вт, 1 Вт или даже 10 Вт того же сопротивления (Ом). Это даже повысит надежность схемы, так как компонент будет меньше греться. Единственные ограничения — это габариты (мощные резисторы крупнее) и цена. А вот ставить резистор меньшей мощности категорически запрещено.

Что означают цветные полоски на корпусе?

Это цветовая маркировка номинала, принятая потому, что на маленьких деталях цифры сложно читать и они могут стереться. Обычно используется 4 полосы: первые две — цифры, третья — множитель (количество нулей), четвертая — допуск (точность). Например, Золотистая полоска в конце означает допуск ±5%.

Чем отличается «импеданс» от обычного сопротивления?

Обычное сопротивление $ R $ постоянно и работает на постоянном токе. Импеданс $ Z $ — это полное сопротивление цепи переменному току, которое включает в себя не только резистивную (активную) часть, но и реактивную (емкостную и индуктивную). Импеданс зависит от частоты сигнала, тогда как сопротивление идеального резистора от частоты не зависит.

Нормативная база

ГОСТ 2.728-74 — Обозначения условные графические в схемах. Резисторы, конденсаторы.
ГОСТ 28883-90 — Резисторы постоянные и переменные. Термины и определения.
ГОСТ Р 50463-92 — Резисторы постоянные для электронной аппаратуры. Общие технические условия.

Рекомендуемая литература:

Бессонов Л. А.* Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2020. (Классический вузовский учебник).
Хоровиц П., Хилл У.* Искусство схемотехники. — М.: Мир, 2018. (Библия современной электроники, глава 1).
Матханов П. Н.* Основы анализа электрических цепей. — М.: Высшая школа, 1981.