Расчет электрических цепей прямым методом Кирхгофа

Содержание страницы

1. Теоретические основы и алгоритм расчета
2. Топологические особенности и использование графов
3. Практический пример расчета
4. Передаточные коэффициенты и проводимости
5. Сравнительный анализ методов расчета цепей
6. Преимущества и недостатки метода Кирхгофа
7. Интересные факты о законах Кирхгофа
8. Часто задаваемые вопросы (FAQ)
Заключение

Расчет электрических цепей с помощью законов Кирхгофа является фундаментальным, наиболее универсальным и прямым методом анализа в электротехнике. Сформулированные немецким физиком Густавом Кирхгофом в 1845 году, эти законы базируются на фундаментальных принципах сохранения заряда и энергии. В отличие от частных методик (таких как метод контурных токов или метод узловых потенциалов), непосредственное применение законов Кирхгофа позволяет описать цепь любой конфигурации и сложности без предварительных преобразований схемы.

В современной инженерной практике, при наличии вычислительных комплексов типа MathCAD, MATLAB или мобильных приложений Math Studio, данный метод остается актуальным для выполнения расчетов весьма сложных разветвленных электрических цепей, где ручное решение системы уравнений было бы трудоемким.

Примечание: Прямое применение законов Кирхгофа часто используется в программных симуляторах (SPICE-подобных) на нижнем уровне абстракции для формирования разреженных матриц системы линейных алгебраических уравнений (СЛАУ), описывающих моделируемое устройство.

1. Теоретические основы и алгоритм расчета

Наиболее распространенной инженерной задачей является анализ, при котором известны все параметры пассивных элементов (сопротивления $R$), источники тока ($J$) и ЭДС ($E$), а требуется определить токи во всех ветвях разветвленной цепи. Корректное применение метода требует строгого соблюдения последовательности действий.

1.1. Последовательность выполнения расчета

Выбор условных положительных направлений токов: В каждой ветви произвольно задаются направления токов. Если в результате расчета значение тока получается отрицательным, это означает, что его истинное направление противоположно выбранному.
Обозначение направлений обхода контуров: Для каждого выбранного контура задается направление его обхода (по часовой или против часовой стрелки), необходимое для составления уравнений по второму закону Кирхгофа.
Составление системы уравнений: Записываются уравнения по первому и второму законам Кирхгофа.
Решение системы уравнений: Используются алгебраические методы (метод подстановки, метод Крамера, матричный метод и др.) для нахождения неизвестных токов.
Верификация результатов: Проверка правильности расчета путем составления баланса мощностей.

1.2. Определение необходимого числа уравнений

Для цепи, содержащей $x$ ветвей и $y$ узлов, где $x_i$ — количество ветвей, содержащих идеальные источники тока, необходимо составить систему из $x — x_i$ уравнений. Это количество соответствует числу неизвестных токов в ветвях без источников тока (ток в ветви с источником тока известен заранее и равен $J$).

По первому закону Кирхгофа (для узлов) составляется $y — 1$ независимых уравнений.
По второму закону Кирхгофа (для контуров) составляется оставшаяся часть уравнений: $x — x_i — (y — 1)$.

2. Топологические особенности и использование графов

Для сложных электрических цепей с большим числом ветвей критически важным является выбор независимых контуров при составлении уравнений по второму закону Кирхгофа. Если выбрать зависимые контуры, полученная система уравнений будет линейно зависимой и не будет иметь единственного решения. Избежать этого позволяет использование элементов теории графов.

Граф электрической цепи отображает ее топологию: вершины графа соответствуют узлам схемы, а ребра — ветвям. Для построения системы независимых контуров используется понятие дерева графа.

Дерево графа — это связная часть графа, содержащая все его вершины, но не содержащая ни одного контура (замкнутого пути).
Хорды (ветви связи) — это ветви, не вошедшие в дерево. Добавление любой одной хорды к дереву образует ровно один независимый (фундаментальный) контур.

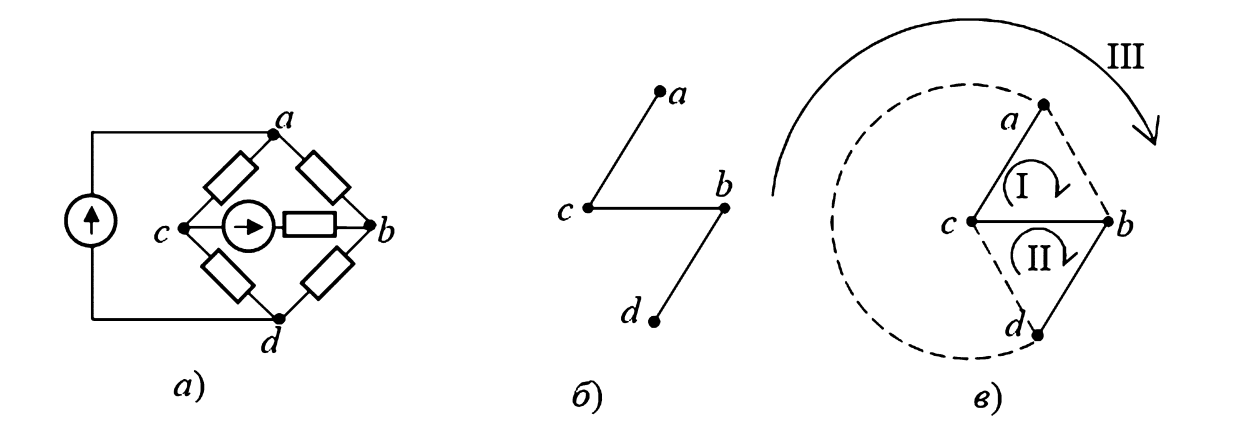
Рисунок 1. Электрическая цепь и ее граф: а — схема цепи; б — дерево графа; в — граф цепи (пунктиром проведены хорды и стрелками показаны образованные контуры).

Как показано на рисунке 1, для выделения независимых контуров сначала рисуют дерево графа (рис. 1б), соединяя все узлы так, чтобы не образовывалось замкнутых путей. Затем поочередно добавляют недостающие ветви — хорды (рис. 1в). Каждый образованный таким образом контур является независимым, и для него записывается уравнение по второму закону Кирхгофа.

3. Практический пример расчета

Рассмотрим применение метода на конкретном примере. Требуется определить токи в ветвях схемы, представленной на рисунке 2.

Дано: $E_1 = 110$ В, $E_2 = 64$ В, $J = 4$ А; $R_1 = 6$ Ом, $R_2 = 4$ Ом, $R_3 = 3$ Ом, $R_4 = 1$ Ом.

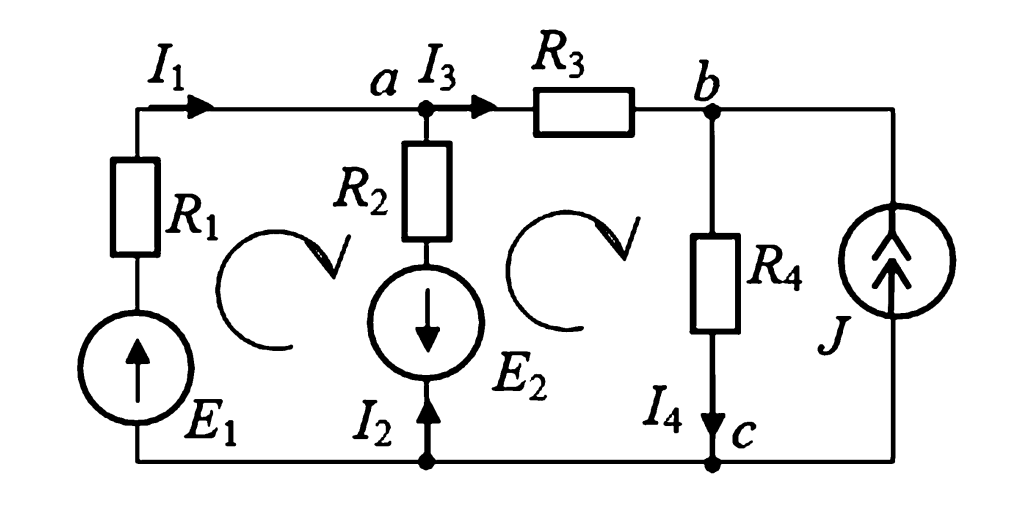
Рисунок 2. Схема электрической цепи к примеру расчета.

Решение:

Шаг 1. Топологический анализ.
Определяем параметры схемы: число ветвей $x = 5$, из них с источником тока $x_i = 1$. Число узлов $y = 3$ (в узле «c» сходятся 4 ветви).
Необходимо составить $x — x_i = 5 — 1 = 4$ уравнения для нахождения токов $I_1, I_2, I_3, I_4$.

Шаг 2. Уравнения по первому закону Кирхгофа.
Число уравнений: $y — 1 = 3 — 1 = 2$. Составим их для узлов $a$ и $b$:
$$ \text{Узел } a: \quad I_1 + I_2 — I_3 = 0 $$
$$ \text{Узел } b: \quad I_3 + J — I_4 = 0 $$
Примечание: ток источника тока $J$ учитывается как известный входящий в узел ток.

Шаг 3. Уравнения по второму закону Кирхгофа.
Число уравнений: $4 — 2 = 2$. Выберем левый и центральный контуры.
При составлении уравнений слагаемые берутся со знаком «+», если направление тока или ЭДС совпадает с направлением обхода контура, и со знаком «–» в противном случае.
$$ \text{Левый контур: } \quad I_1 R_1 — I_2 R_2 = E_1 + E_2 $$
$$ \text{Центральный контур: } \quad I_2 R_2 + I_3 R_3 + I_4 R_4 = -E_2 $$
Важно: Контур не должен проходить через ветвь с идеальным источником тока $J$, так как его внутреннее сопротивление бесконечно велико, и падение напряжения на нем неизвестно до окончания расчета остальных токов.

Шаг 4. Решение системы.
Подставив численные значения, получаем систему:
$$ \begin{cases} I_1 + I_2 — I_3 = 0 \\ I_3 + 4 — I_4 = 0 \\ 6I_1 — 4I_2 = 110 + 64 \\ 4I_2 + 3I_3 + 1 \cdot I_4 = -64 \end{cases} $$
Решая данную систему, находим значения токов:
$$ I_1 = 17,5 \text{ А}; \quad I_2 = -17,25 \text{ А}; \quad I_3 = 0,25 \text{ А}; \quad I_4 = 4,25 \text{ А}. $$
Отрицательное значение $I_2$ указывает на то, что реальное направление тока в этой ветви противоположно выбранному на схеме.

Шаг 5. Проверка баланса мощностей.
Баланс мощностей подтверждает выполнение закона сохранения энергии: сумма мощностей, генерируемых источниками, должна быть равна сумме мощностей, потребляемых приемниками.
$$ \sum P_{ген} = \sum P_{потр} $$
Мощность потребителей (на резисторах):
$$ P_{потр} = I_1^2 R_1 + I_2^2 R_2 + I_3^2 R_3 + I_4^2 R_4 $$
$$ P_{потр} = 17,5^2 \cdot 6 + (-17,25)^2 \cdot 4 + 0,25^2 \cdot 3 + 4,25^2 \cdot 1 = 3046 \text{ Вт} $$
Мощность источников:
$$ P_{ген} = E_1 I_1 — E_2 I_2 + U_{bc} J $$
Слагаемое $E_2 I_2$ взято с минусом, так как выбранные направления ЭДС $E_2$ и тока $I_2$ встречны. $U_{bc}$ — напряжение на зажимах источника тока, равное $I_4 R_4$ (исходя из топологии схемы, где ветвь с $J$ параллельна ветви с $R_3$ и последовательной цепочке). В данном примере использовано расчетное значение мощности источника тока $U_{bc} J = (4,25 \cdot 1) \cdot 4$.
$$ P_{ген} = 110 \cdot 17,5 + 64 \cdot 17,25 + 4,25 \cdot 1 \cdot 4 = 3046 \text{ Вт} $$
Примечание: При подстановке $I_2 = -17,25$ А в формулу с учетом знака перед слагаемым ($- E_2 I_2$) получается положительный вклад в генерируемую мощность, что физически корректно.
Поскольку $P_{ген} = P_{потр} = 3046$ Вт, расчет выполнен верно.

4. Передаточные коэффициенты и проводимости

Линейность электрических цепей позволяет представить токи в ветвях как линейную комбинацию воздействующих ЭДС и токов источников. После решения системы уравнений, токи можно выразить в общем виде:

$$ I_m = \sum_{n} g_{mn} E_n + \sum_{k} h_{mk} J_k $$

где $E_n$ — ЭДС в ветви $n$, а $J_k$ — источники тока, подключенные к узлам.

Входная (собственная) проводимость ($g_{mm}$): Коэффициент с одинаковыми индексами. Численно равен току в ветви $m$, вызванному ЭДС в 1 В, включенной в эту же ветвь, при отсутствии других источников в цепи. Величина, обратная входной проводимости, называется входным сопротивлением: $R_{вх} = 1/g_{mm}$.
Взаимная (передаточная) проводимость ($g_{mn}$): Коэффициент с разными индексами. Равен току в ветви $m$, вызванному действием ЭДС в 1 В, находящейся в ветви $n$. Согласно принципу взаимности, для линейных пассивных цепей $g_{mn} = g_{nm}$.
Передаточный коэффициент по току ($h_{nk}$): Безразмерная величина, численно равная току в ветви $n$ при действии единственного источника тока $J_k = 1$ А.

Эти коэффициенты зависят исключительно от топологии цепи и номиналов пассивных элементов (резисторов), но не зависят от значений самих источников ЭДС или тока. Их можно определить опытно или расчетно, поочередно «включая» только один единичный источник и «обнуляя» остальные.

5. Сравнительный анализ методов расчета цепей

Хотя законы Кирхгофа универсальны, существуют и другие методы, которые могут быть более эффективны в определенных ситуациях. Ниже приведена таблица сравнения основных методов.

Метод расчета	Основная идея	Количество уравнений	Преимущества	Недостатки
Законы Кирхгофа (прямой метод)	Составление уравнений для токов ветвей на базе I и II законов.	Максимальное ($x — x_i$)	Универсальность, физическая наглядность всех переменных (реальные токи).	Громоздкая система уравнений для больших цепей, высокая вероятность ошибки при ручном расчете.
Метод контурных токов (МКТ)	Введение фиктивных контурных токов, автоматически удовлетворяющих I закону Кирхгофа.	Меньше ($x — y + 1 — x_i$)	Уменьшение порядка системы уравнений, удобен для планарных схем.	Требует последующего вычисления реальных токов ветвей через контурные.
Метод узловых потенциалов (МУП)	Определение потенциалов узлов относительно базисного. Автоматически удовлетворяет II закону Кирхгофа.	Минимальное для многих схем ($y — 1$)	Наиболее эффективен для схем с большим числом параллельных ветвей и малым числом узлов. Часто используется в ПО.	Менее нагляден, требует пересчета потенциалов в токи ветвей.

6. Преимущества и недостатки метода Кирхгофа

Преимущества

Универсальность: Применим к любой электрической цепи — линейной, нелинейной, постоянного или переменного тока, стационарной или нестационарной.
Прямой результат: В ходе решения сразу находятся искомые токи ветвей, без промежуточных фиктивных величин (как в МКТ или МУП).
Наглядность: Уравнения имеют ясный физический смысл, напрямую отражающий законы сохранения.

Недостатки

Высокая размерность системы: Количество уравнений равно числу неизвестных токов, что для сложных схем ведет к системам высокого порядка.
Трудоемкость: Высокая вероятность допустить арифметическую ошибку при ручном решении больших систем.

7. Интересные факты о законах Кирхгофа

Возраст открытия: Густав Кирхгоф сформулировал свои знаменитые законы в 1845 году, будучи еще студентом. Ему был всего 21 год.
Не только электричество: Аналоги законов Кирхгофа применяются в других областях физики и техники, например, в гидравлических расчетах (расчет трубопроводных сетей), тепловых цепях и даже в экономическом моделировании потоков.
Связь с уравнениями Максвелла: В строгом смысле законы Кирхгофа являются следствием уравнений Максвелла для квазистационарного режима, когда изменением магнитного поля во времени можно пренебречь для рассматриваемых размеров цепи.
Ограничения применимости: Законы Кирхгофа в их классической форме справедливы только для цепей с сосредоточенными параметрами. Если геометрические размеры цепи соизмеримы с длиной волны электромагнитного поля (высокочастотные цепи, длинные линии электропередач), вступают в силу волновые процессы, и требуются уравнения длинных линий (телеграфные уравнения).
Связь с фундаментальной физикой: С математической точки зрения, первый закон Кирхгофа является следствием закона сохранения электрического заряда и уравнения непрерывности, а второй закон — следствием потенциальности стационарного электрического поля (равенства нулю ротора поля в отсутствие изменяющегося магнитного потока).
Применение в биологии: Принципы Кирхгофа используются не только в технике, но и в биофизике, например, в модели Ходжкина-Хаксли для описания распространения нервных импульсов, где мембрана клетки моделируется как электрическая цепь с емкостями и переменными сопротивлениями.
Топологическая инвариантность: Уравнения Кирхгофа зависят только от способа соединения элементов (топологии), но не от природы самих элементов. Это позволяет использовать одни и те же топологические матрицы для расчета цепей с резисторами, конденсаторами, индуктивностями и даже механических или гидравлических аналогов.

8. Часто задаваемые вопросы (FAQ)

Вопрос: Что делать, если в цепи есть только источники тока и нет источников ЭДС?

Ответ: Метод применяется аналогично, но количество неизвестных уменьшается. Уравнения составляются относительно токов в ветвях с резисторами. Важно помнить, что узловые уравнения должны учитывать токи источников.

Вопрос: Как выбрать «правильный» контур для второго закона Кирхгофа?

Ответ: Главное правило — каждый новый выбранный контур должен содержать хотя бы одну ветвь, которая не входила в ранее выбранные контуры. Использование «дерева графа» и «хорд» гарантирует выполнение этого правила.

Вопрос: Можно ли применять законы Кирхгофа для цепей переменного тока?

Ответ: Да, безусловно. В цепях синусоидального переменного тока законы Кирхгофа записываются в комплексной форме (для комплексных амплитуд токов и ЭДС), а сопротивления заменяются комплексными импедансами $Z$.

Вопрос: Почему баланс мощностей может не сходиться при расчете?

Ответ: Наиболее частые причины: арифметическая ошибка при решении системы, неправильно определенные знаки мощностей источников (если ток входит в «плюс» источника ЭДС, он потребляет мощность, а не генерирует), или некорректный учет мощности источников тока.

Вопрос: Что делать, если в схеме присутствуют зависимые (управляемые) источники тока или ЭДС?

Ответ: Зависимые источники при первичном составлении уравнений Кирхгофа учитываются так же, как и независимые. Однако в систему уравнений необходимо добавить дополнительные уравнения связи, выражающие величину управляемого источника через токи или напряжения других ветвей, от которых он зависит.

Вопрос: Как применяется метод, если электрическая цепь является непланарной (ее невозможно начертить на плоскости без пересечения ветвей)?

Ответ: Прямой метод применения законов Кирхгофа (в отличие от метода контурных токов, использующего ячейки плоской схемы) универсален и подходит для непланарных цепей. В этом случае особенно важно использовать аппарат теории графов (дерево и хорды) для гарантированного выбора системы независимых контуров.

Заключение

Несмотря на развитие мощных программных средств автоматизированного проектирования, понимание и умение применять законы Кирхгофа остается базовым навыком любого инженера-электрика. Эти законы служат «фундаментом», на котором строятся все остальные, более изощренные методы анализа цепей. Они обеспечивают прямую связь между математической моделью и физическими процессами протекания тока и распределения потенциалов в устройстве.

Нормативная база и литература

ГОСТ Р 52002-2003 Электротехника. Термины и определения основных понятий.
ГОСТ 2.702-2011 Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2016.
Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. — М.: Энергоатомиздат, 1989.