Расчет разветвленной электрической цепи синусоидального тока

Содержание страницы

1. Законы Кирхгофа в комплексной форме
2. Методы расчета на основе комплексных чисел
3. Визуализация расчетов: Векторные и топографические диаграммы
4. Пример: Расчет разветвленной цепи и построение диаграмм
5. Программное обеспечение для расчетов
6. Интересные факты по теме
7. Часто задаваемые вопросы (FAQ)
Заключение

Расчет электрических цепей является основной задачей электротехники. Если в цепях постоянного тока (DC) основными параметрами являются сопротивление (R), ток (I) и напряжение (U), то при переходе к цепям синусоидального (переменного) тока (AC) анализ значительно усложняется. Это связано с появлением реактивных элементов — индуктивностей (L) и емкостей (C), которые вносят фазовые сдвиги между током и напряжением.

Для описания таких цепей с помощью мгновенных значений пришлось бы решать системы дифференциальных уравнений, что крайне трудоемко. Революционный прорыв в этой области произошел в конце XIX века благодаря работам Оливера Хевисайда и, в особенности, Чарльза Протеуса Штейнмеца. Они предложили использовать комплексные числа для представления синусоидальных величин (токов и напряжений) в виде векторов (фазоров) на комплексной плоскости. Этот подход, известный как символический метод или метод комплексных амплитуд, преобразует сложные дифференциальные уравнения в относительно простые алгебраические уравнения с комплексными коэффициентами.

Данный материал посвящен применению этого мощного аппарата для расчета разветвленных AC-цепей, в частности, использованию законов Кирхгофа в их комплексной форме и наглядной интерпретации результатов с помощью векторных и топографических диаграмм.

1. Законы Кирхгофа в комплексной форме

Основой расчета любой сложной цепи служат законы Кирхгофа. Для их применения в цепях синусоидального тока необходимо перейти от мгновенных значений к комплексным амплитудам.

Мгновенное значение тока $i_k(t)$ в $k$-й ветви можно представить через комплексную амплитуду (фазор) $\dot{I}_k$:
$$i_k(t) = \text{Im}(\dot{I}_k e^{j\omega t})$$
где $\omega$ — угловая частота, а $\dot{I}_k$ — комплексное число, модуль которого равен действующему значению тока, а аргумент — начальной фазе.

Первый закон Кирхгофа (в комплексной форме)

Первый закон Кирхгофа для мгновенных значений гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю: $\sum_k i_k(t) = 0$. Подставим сюда комплексное представление:

$$\sum_k \text{Im}(\dot{I}_k e^{j\omega t}) = \text{Im}\left( \left(\sum_k \dot{I}_k\right) e^{j\omega t} \right) = 0$$

Это равенство должно выполняться в любой момент времени $t$. Это возможно только в том случае, если комплексная сумма в скобках сама равна нулю. Таким образом, получаем первый закон Кирхгофа в комплексной форме:

$$ \sum_k \dot{I}_k = 0 $$

Этот закон утверждает, что геометрическая (векторная) сумма комплексных токов в любом узле схемы равна нулю. Это обеспечивает баланс не только амплитуд, но и фаз.

Второй закон Кирхгофа (в комплексной форме)

Аналогично, второй закон Кирхгофа для мгновенных значений (сумма падений напряжений в замкнутом контуре равна сумме ЭДС) $\sum_k u_k(t) = \sum_k e_k(t)$ преобразуется в комплексную форму.

Учитывая, что комплексное падение напряжения на элементе с импедансом $Z_k$ равно $\dot{U}_k = \dot{I}_k Z_k$, а ЭДС представляется комплексом $\dot{E}_k$, получаем второй закон Кирхгофа в комплексной форме:

$$ \sum_k \dot{U}_k = \sum_k \dot{E}_k $$

Или, в более развернутом виде:

$$ \sum_k \dot{I}_k Z_k = \sum_k \dot{E}_k $$

Это уравнение означает, что в любом замкнутом контуре цепи векторная сумма комплексных падений напряжений на всех элементах равна векторной сумме комплексных ЭДС, действующих в этом контуре.

2. Методы расчета на основе комплексных чисел

В предыдущих главах (при анализе цепей постоянного тока) были получены на основе законов Кирхгофа специальные методы расчета разветвленных цепей — метод контурных токов, метод узловых потенциалов и другие.

Огромное преимущество символического метода заключается в том, что все эти методы сохраняют свою полную применимость для расчета цепей при синусоидальных токах. Единственное, что требуется — это произвести формальную замену:

Активные сопротивления $R$ заменяются на комплексные сопротивления (импедансы) $Z$.
Вещественные токи $I_k$ заменяются на комплексы токов $\dot{I}_k$.
Вещественные ЭДС $E_k$ заменяются на комплексы ЭДС $\dot{E}_k$.

Примечание: Переход к комплексным числам — это, по сути, переход от решения систем линейных дифференциальных уравнений к решению систем линейных алгебраических уравнений (СЛАУ). Матрица коэффициентов такой СЛАУ будет состоять из комплексных импедансов, вектор неизвестных — из комплексных токов (в методе контурных токов) или потенциалов (в методе узловых потенциалов), а вектор свободных членов — из комплексных ЭДС. Это кардинально упрощает математический аппарат анализа.

Сравнение анализа цепей DC и AC

Для наглядности приведем сравнительную таблицу подходов к расчету.

Параметр	Расчет цепей постоянного тока (DC)	Расчет цепей синусоидального тока (AC)
Основные величины	Ток (I), Напряжение (U), ЭДС (E) — скалярные величины.	Комплексы тока ($\dot{I}$), напряжения ($\dot{U}$), ЭДС ($\dot{E}$) — векторные (комплексные) величины.
Сопротивление	Активное сопротивление (R).	Комплексное сопротивление (импеданс, $Z = R + jX$), где X — реактивное сопротивление.
Закон Ома	$I = U / R$	$\dot{I} = \dot{U} / Z$ (Закон Ома в комплексной форме)
Математический аппарат	Алгебраические уравнения с вещественными числами.	Алгебраические уравнения с комплексными числами.
Учет фазы	Не требуется, фазовых сдвигов нет.	Обязателен. Фаза определяется аргументом комплексного числа.
Мощность	Активная мощность $P = UI$.	Полная мощность $S = P + jQ = \dot{U}\dot{I}^*$, где P — активная, Q — реактивная.

Преимущества и недостатки комплексного метода

Преимущества:

Унификация: Позволяет единообразно описывать поведение резисторов ($Z_R = R$), катушек индуктивности ($Z_L = j\omega L$) и конденсаторов ($Z_C = -j/(\omega C)$).
Алгебраизация: Сводит решение дифференциальных уравнений к алгебраическим операциям (сложение, вычитание, умножение, деление) с комплексными числами.
Полнота информации: Результат расчета (например, $\dot{I} = a + jb$) немедленно дает и амплитуду (модуль) тока, и его фазовый сдвиг (аргумент) относительно опорного напряжения.

Недостатки:

Математическая сложность: Требует уверенного владения операциями с комплексными числами (перевод из алгебраической в показательную форму и обратно).
Абстрактность: Начинающим инженерам может быть сложно развить «физическое чутье» для комплексных величин до построения наглядных диаграмм.
Ограничение применимости: Метод напрямую применим только для линейных цепей и только в установившемся синусоидальном режиме. Для несинусоидальных токов требуется разложение в ряд Фурье.

3. Визуализация расчетов: Векторные и топографические диаграммы

Аналитические расчеты электрических цепей синусоидального тока настоятельно рекомендуется сопровождать построением векторных диаграмм. Это делается для того, чтобы иметь возможность качественно контролировать эти расчеты и наглядно представлять фазовые соотношения между величинами.

Векторная диаграмма — это совокупность векторов на комплексной плоскости, изображающих комплексные амплитуды токов и напряжений в цепи. По ней можно графически проверить выполнение законов Кирхгофа (например, сумма векторов токов в узле должна давать нулевой вектор).

В некоторых случаях, для более детального анализа, строят топографические диаграммы, на которых отражены комплексные потенциалы всех точек (узлов) электрической цепи с учетом ее топографии (схемы соединения).

Особенности топографических диаграмм

Топографическая диаграмма — это, по сути, «карта» потенциалов цепи на комплексной плоскости. Потенциал одной из точек (обычно «земля» или общий провод) принимается за ноль ($\dot{\phi}_{ref} = 0$), и относительно этой точки откладываются потенциалы всех остальных узлов.

Это позволяет определить разность потенциалов (напряжение) между *любыми* двумя точками электрической цепи, просто измерив расстояние (вектор) между этими точками на диаграмме и умножив его на масштаб.

При построении топографических диаграмм следует иметь в виду, что разность потенциалов $\dot{U}_{ab} = \dot{\phi}_a — \dot{\phi}_b$ (напряжение между точками ‘a’ и ‘b’) изображается на комплексной плоскости (рис. 1в) вектором, направленным к точке ‘a’ (от ‘b’ к ‘a’). В то же время, на электрической схеме эта разность потенциалов изображается стрелкой, направленной в порядке чередования индексов (от ‘a’ к ‘b’). Важно не путать эти два соглашения.

Так как ток направлен от точки с более высоким потенциалом к точке с более низким, а стрелки векторов на диаграмме будут направлены к более высокому потенциалу (при обходе против тока), построение топографической диаграммы следует выполнять, двигаясь от точки к точке против направления тока. В этом случае:

Векторы падений напряжений на резисторах ($\dot{U}_R = \dot{I}R$) будут параллельны (сонаправлены) векторам токов на этих резисторах.
Векторы падений напряжений на индуктивностях ($\dot{U}_L = jX_L \dot{I}$) будут перпендикулярны к соответствующим токам и повернуты против направления вращения часовой стрелки (опережают ток на $\pi/2$ или 90°).
Векторы падений напряжений на конденсаторах ($\dot{U}_C = -jX_C \dot{I}$) будут перпендикулярны соответствующим токам и повернуты по направлению вращения часовой стрелки (отстают от тока на $\pi/2$ или 90°).

4. Пример: Расчет разветвленной цепи и построение диаграмм

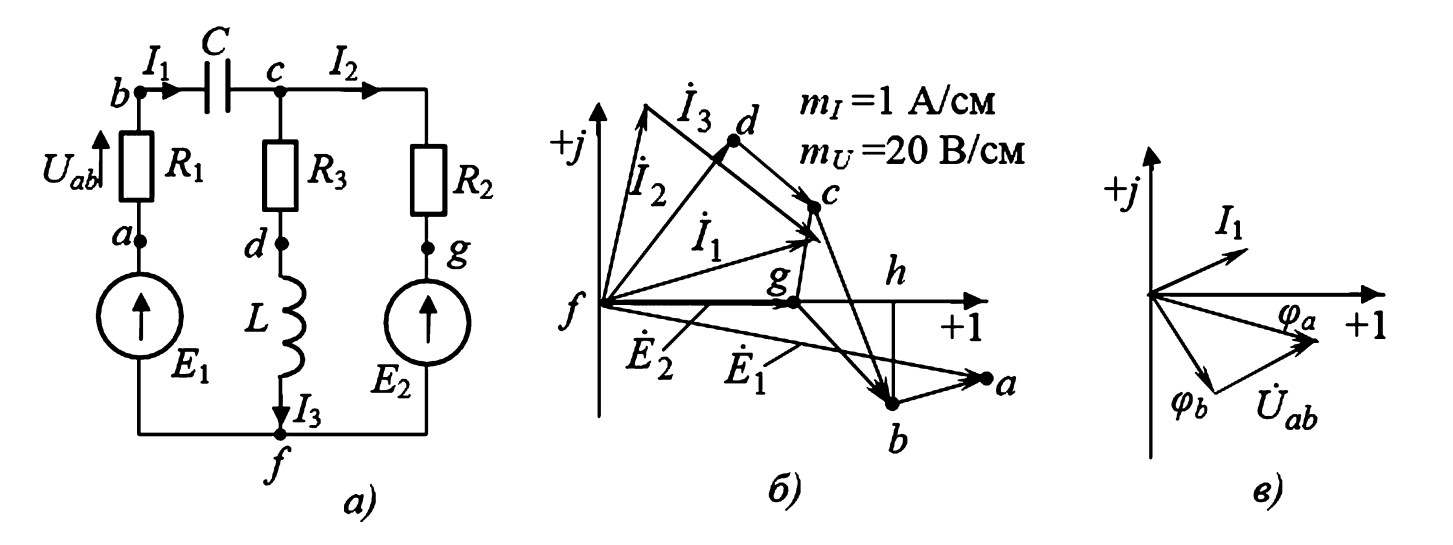
Задача: Определить токи в электрической цепи (рис. 1а) и построить топографическую диаграмму, если заданы следующие параметры:

$\dot{E}_1 = (200 — j40)$ В
$\dot{E}_2 = 100$ В (или $100 + j0$ В)
$R_1 = R_2 = R_3 = 10$ Ом
$X_L = 20$ Ом (Индуктивное сопротивление)
$X_C = 20$ Ом (Емкостное сопротивление)

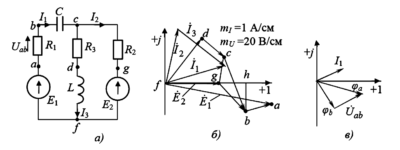
Рисунок 1. Расчет разветвленной цепи: а — схема цепи; б — топографическая диаграмма; в — разность потенциалов.

Решение

1. Определение комплексных сопротивлений (импедансов) ветвей:

Импеданс первой ветви (a-b-c) содержит резистор $R_1$ и конденсатор $X_C$:
$$Z_1 = R_1 — jX_C = (10 — j20) \text{ Ом}$$

Импеданс второй ветви (g-c) содержит только резистор $R_2$:
$$Z_2 = R_2 = 10 \text{ Ом}$$

Импеданс третьей ветви (f-d-c) содержит резистор $R_3$ и катушку индуктивности $X_L$:
$$Z_3 = R_3 + jX_L = (10 + j20) \text{ Ом}$$

2. Определение напряжения между узлами $U_{cf}$:

Для определения напряжения между узлами ‘c’ и ‘f’ воспользуемся методом двух узлов (частный случай метода узловых потенциалов). Примем потенциал узла ‘f’ равным нулю ($\dot{\phi}_f = 0$). Тогда $\dot{U}_{cf} = \dot{\phi}_c$.

Формула для метода двух узлов:

$$ \dot{U}_{cf} = \frac{\dot{E}_1/Z_1 + \dot{E}_2/Z_2 + \dot{E}_3/Z_3}{1/Z_1 + 1/Z_2 + 1/Z_3} $$

В нашем случае в третьей ветви нет ЭДС ($\dot{E}_3 = 0$), а $\dot{E}_2$ направлена к узлу ‘f’, поэтому в числителе она будет со знаком «минус» (или, что то же самое, напряжение на узле g относительно f равно $\dot{E}_2$). Формула примет вид:

$$ \dot{U}_{cf} = \frac{\dot{E}_1/Z_1 + \dot{E}_2/Z_2}{1/Z_1 + 1/Z_2 + 1/Z_3} $$

Детальный расчет $\dot{U}_{cf}$:
Сначала найдем проводимости ветвей (Y = 1/Z):

$Y_1 = 1 / (10 — j20) = (10 + j20) / (10^2 + 20^2) = (10 + j20) / 500 = (0.02 + j0.04)$ См
$Y_2 = 1 / 10 = 0.1$ См
$Y_3 = 1 / (10 + j20) = (10 — j20) / (10^2 + 20^2) = (10 — j20) / 500 = (0.02 — j0.04)$ См

Сумма проводимостей в знаменателе:
$$ \sum Y_k = (0.02 + j0.04) + 0.1 + (0.02 — j0.04) = 0.14 \text{ См} $$
Сумма токов в числителе:

$\dot{E}_1 Y_1 = (200 — j40) \cdot (0.02 + j0.04) = 4 + j8 — j0.8 + 1.6 = 5.6 + j7.2$ А
$\dot{E}_2 Y_2 = 100 \cdot 0.1 = 10$ А

Сумма в числителе: $(5.6 + j7.2) + 10 = 15.6 + j7.2$ А.

Искомое напряжение:
$$ \dot{U}_{cf} = (15.6 + j7.2) / 0.14 \approx (111.4 + j51.4) \text{ В} $$
(В исходном тексте приведено округленное значение $111 + j51.5$ В, будем использовать его для согласованности).

Итак, принимаем $\dot{U}_{cf} \approx (111 + j51.5)$ В.

3. Расчет токов в ветвях:

Токи определяются по обобщенному закону Ома для каждой ветви:

Ветвь 1:
$$ \dot{I}_1 = \frac{\dot{E}_1 — \dot{U}_{cf}}{Z_1} = \frac{(200 — j40) — (111 + j51.5)}{10 — j20} = \frac{89 — j91.5}{10 — j20} $$
$$ \dot{I}_1 \approx (5.5 + j1.7) \text{ А} \quad (\text{или } 5.76 \cdot e^{j17^\circ} \text{ А}) $$
Ветвь 2: (Ток течет от ‘c’ к ‘g’, т.к. $\dot{U}_{cf}$ > $\dot{E}_2$)
$$ \dot{I}_2 = \frac{\dot{U}_{cf} — \dot{E}_2}{Z_2} = \frac{(111 + j51.5) — 100}{10} = \frac{11 + j51.5}{10} $$
$$ \dot{I}_2 = (1.1 + j5.1) \text{ А} \quad (\text{или } 5.2 \cdot e^{j78^\circ} \text{ А}) $$
Ветвь 3:
$$ \dot{I}_3 = \frac{\dot{U}_{cf}}{Z_3} = \frac{111 + j51.5}{10 + j20} $$
$$ \dot{I}_3 \approx (4.3 — j3.4) \text{ А} \quad (\text{или } 5.5 \cdot e^{-j38.3^\circ} \text{ А}) $$

Проверка по первому закону Кирхгофа (для узла ‘c’): $\dot{I}_1 = \dot{I}_2 + \dot{I}_3$
$(1.1 + j5.1) + (4.3 — j3.4) = (5.4 + j1.7)$ А. Это практически совпадает с $\dot{I}_1 \approx (5.5 + j1.7)$ А (расхождение связано с округлением в исходных данных).

4. Построение топографической диаграммы (рис. 1б):

Строим на комплексной плоскости треугольник токов, откладывая сначала ток $\dot{I}_2$, а затем к нему прибавляя ток $\dot{I}_3$ и замыкая их сумму током $\dot{I}_1$. Масштаб выбираем произвольно, например $m_I = 1$ А/см.

Построение топографической диаграммы начнем с точки ‘f’, считая ее потенциал равным нулю ($\dot{\phi}_f = 0$).

Определим потенциал точки ‘d’. Двигаемся от ‘f’ к ‘d’ (против тока $\dot{I}_3$). Падение напряжения на катушке $X_L$ равно:
$$\dot{U}_{df} = \dot{I}_3 \cdot (jX_L) = (4.3 — j3.4) \cdot j20 = 68 + j86 \text{ В}$$
Поскольку $\dot{\phi}_f = 0$, то $\dot{\phi}_d = \dot{U}_{df} = (68 + j86)$ В. Выбираем масштаб напряжений (например, $m_U = 20$ В/см) и откладываем по оси абсцисс отрезок $68/20 = 3.4$ см, а по оси ординат — $86/20 = 4.3$ см. По этим проекциям строим вектор $\dot{U}_{df}$ (стрелка на диаграмме направлена к точке ‘d’). Отмечаем, что вектор $\dot{U}_{df}$ перпендикулярен току $\dot{I}_3$ и опережает его на 90°.
Определим потенциал точки ‘c’. Двигаемся от ‘d’ к ‘c’ (против тока $\dot{I}_3$). Падение напряжения на резисторе $R_3$ равно:
$$\dot{U}_{cd} = \dot{I}_3 \cdot R_3 = (4.3 — j3.4) \cdot 10 = 43 — j34 \text{ В}$$
Отложим этот вектор из конца вектора $\dot{U}_{df}$ (т.е. из точки ‘d’). Вектор $\dot{U}_{cd}$ параллелен вектору $\dot{I}_3$. Конец этого вектора даст нам точку ‘c’.Проверка: $\dot{\phi}_c = \dot{\phi}_d + \dot{U}_{cd} = (68 + j86) + (43 — j34) = (111 + j52)$ В. Это совпадает с нашим расчетным значением $\dot{U}_{cf}$ (с учетом округлений).
Двигаемся по первой ветви от ‘c’ к ‘a’ (против тока $\dot{I}_1$). Сначала отложим напряжение на конденсаторе $X_C$:
$$\dot{U}_{bc} = \dot{I}_1 \cdot (-jX_C) = (5.5 + j1.7) \cdot (-j20) = 34 — j110 \text{ В}$$
Откладываем этот вектор из точки ‘c’. Он должен быть перпендикулярен $\dot{I}_1$ и отставать от него на 90°.
Затем отложим напряжение на резисторе $R_1$:
$$\dot{U}_{ab} = \dot{I}_1 \cdot R_1 = (5.5 + j1.7) \cdot 10 = 55 + j17 \text{ В}$$
Откладываем этот вектор из конца $\dot{U}_{bc}$ (т.е. из точки ‘b’) параллельно вектору $\dot{I}_1$. Конец этого вектора даст точку ‘a’.
Сумма всех этих напряжений $\dot{U}_{af} = \dot{U}_{ab} + \dot{U}_{bc} + \dot{U}_{cd} + \dot{U}_{df}$ неверна. Сумма напряжений $\dot{U}_{ab} + \dot{U}_{bc} + \dot{U}_{cf}$ должна быть равна $\dot{E}_1$.Корректная проверка: Потенциал точки ‘a’ равен $\dot{\phi}_a = \dot{\phi}_c + \dot{U}_{bc} + \dot{U}_{ab} = (111 + j52) + (34 — j110) + (55 + j17) = (200 — j41)$ В.
Вектор $\dot{U}_{af} = \dot{\phi}_a — \dot{\phi}_f = \dot{\phi}_a$. Этот вектор должен быть равен $\dot{E}_1$.
Наше расчетное значение $(200 — j41)$ В практически равно заданному $\dot{E}_1 = (200 — j40)$ В.
Нанесем точку ‘g’. Так как $\dot{E}_2 = 100$ В и направлена от ‘g’ к ‘f’, то $\dot{\phi}_g = 100$ В. На диаграмме точка ‘g’ будет лежать на оси абсцисс на расстоянии $100/20 = 5$ см от начала координат (точки ‘f’).
Соединяя точку ‘g’ с точкой ‘c’, построим вектор напряжения на сопротивлении $R_2$, то есть $\dot{U}_{cg} = \dot{\phi}_c — \dot{\phi}_g = (111 + j51.5) — 100 = 11 + j51.5$ В.Проверка: По закону Ома, $\dot{U}_{cg} = \dot{I}_2 R_2 = (1.1 + j5.1) \cdot 10 = 11 + j51$ В. Вектор $\dot{U}_{cg}$ должен быть параллелен току $\dot{I}_2$. Диаграмма построена верно.

5. Использование топографической диаграммы:

Завершив построение топографической диаграммы, можно с ее помощью определять напряжение между любыми точками электрической цепи. Так, соединив точки ‘b’ и ‘g’ отрезком, измерим его длину и, умножив на масштаб напряжений, определим числовое значение (модуль) напряжения:

$$U_{gb} = |bg| \cdot m_U = 3.5 \text{ см} \cdot 20 \text{ В/см} = 70 \text{ В}$$

Чтобы определить комплекс напряжения $\dot{U}_{bg} = \dot{\phi}_b — \dot{\phi}_g$, необходимо определить проекции вектора, идущего от ‘g’ к ‘b’, на вещественную и мнимую оси. На диаграмме (рис. 1б) отрезок ‘hg’ определяет вещественную часть комплекса $\dot{U}_{bg}$, а отрезок ‘bh’ — мнимую часть.

Для определения угла $\phi$ можно сразу определить:
$$\text{tg}(\phi) = \frac{-|bh|}{|hg|} \rightarrow \phi = -48^\circ$$
Так как вектор ‘bh’ направлен в сторону, противоположную мнимой оси, то взят знак минус (–bh).

5. Программное обеспечение для расчетов

Расчеты разветвленных цепей синусоидального тока, особенно с большим количеством узлов и контуров, вручную весьма трудоемки из-за обилия операций с комплексными числами. Целесообразно выполнять их с помощью специализированных программных пакетов.

В исходном материале упоминаются программы MathCAD и Math Studio. Они существенно упрощают вычисления с комплексными числами, позволяя вводить формулы в естественном, близком к математическому, виде и сразу получать результат. Math Studio (для смартфонов и планшетов) особенно удобен для быстрых расчетов «в поле».

Современные альтернативы:

MATLAB & Simulink: Де-факто промышленный стандарт для инженерных вычислений и моделирования. Позволяет решать СЛАУ с комплексными коэффициентами в матричной форме.
Python: С использованием библиотек cmath (для базовых комплексных операций) и NumPy (для решения сложных матричных уравнений) Python стал мощнейшим, гибким и бесплатным инструментом для электротехнических расчетов.
SPICE-симуляторы (LTspice, Multisim): Программы для схемотехнического моделирования. Они не решают уравнения символически, но проводят симуляцию (в том числе AC-sweep), позволяя получить точные значения токов и напряжений в любой точке схемы без составления уравнений вручную.

Несмотря на мощь ПО, ручной расчет (как в Примере 1) и построение диаграмм остаются незаменимыми для развития инженерной интуиции и проверки адекватности результатов, полученных от машины.

6. Интересные факты по теме

Почему «j», а не «i»? В электротехнике для обозначения мнимой единицы ($\sqrt{-1}$) используется символ $j$, а не $i$. Это сделано во избежание путаницы с общепринятым обозначением мгновенного значения тока $i(t)$.
«Волшебник» Штейнмец: Чарльз Протеус Штейнмец, работая в General Electric в 1890-х годах, не изобрел, но активно популяризовал и внедрил метод комплексных чисел в практику расчетов AC-цепей, что произвело революцию в проектировании энергосистем.
Треугольник мощностей: В AC-цепях существует три вида мощности: активная (P, Вт), реактивная (Q, ВАр) и полная (S, ВА). Они связаны соотношением $S = P + jQ$, которое графически образует «треугольник мощностей», также основанный на комплексных числах.
Резонанс в примере: Внимательный анализ примера 1 показывает, что $X_L = X_C = 20$ Ом. Из-за этого $Z_1 = 10 — j20$, а $Z_3 = 10 + j20$. Их параллельная проводимость $Y_1 + Y_3 = (0.02 + j0.04) + (0.02 — j0.04) = 0.04$ См, то есть является чисто активной. Это пример параллельного резонанса токов в ветвях 1 и 3.
Топографические диаграммы и безопасность: Топографические диаграммы потенциалов имеют важное практическое значение в проектировании систем заземления и молниезащиты. Они позволяют рассчитать «шаговое напряжение» (разность потенциалов между ногами человека) при аварийных ситуациях.
Обобщение метода двух узлов: Использованный в примере «метод двух узлов» является частным случаем «метода узловых потенциалов». Он чрезвычайно эффективен для схем с любым количеством параллельных ветвей, подключенных к двум общим узлам.
Несинусоидальные цепи: Если ток в цепи не является синусоидальным (например, в цепях с выпрямителями, инверторами), комплексный метод в чистом виде неприменим. В этом случае сигнал с помощью ряда Фурье разлагают на сумму синусоидальных гармоник. Затем расчет ведут комплексным методом *для каждой гармоники отдельно*, а итоговый результат получают суммированием (по принципу суперпозиции).

7. Часто задаваемые вопросы (FAQ)

1. Зачем нужны комплексные числа в электротехнике, если ток и напряжение — реальные физические величины?

Комплексные числа — это математический инструмент, который позволяет в одной величине (комплексном числе) закодировать сразу два параметра: амплитуду (через модуль) и фазовый сдвиг (через аргумент). Это позволяет заменить решение громоздких дифференциальных уравнений на простую алгебру.

2. Что физически означает «мнимая» часть тока или напряжения?

«Мнимая» часть не означает «несуществующая». Это компонента синусоиды, которая сдвинута по фазе на 90° (или $\pi/2$) относительно «вещественной» части. Например, в импедансе $Z = R + jX$, $R$ создает падение напряжения, совпадающее по фазе с током (вещественная часть), а $X$ — падение напряжения, сдвинутое на 90° (мнимая часть).

3. Можно ли рассчитать AC-цепь без комплексных чисел?

Да, можно. Для этого используется метод мгновенных значений (например, $i(t) = I_m \sin(\omega t + \phi)$). Однако это требует составления и решения систем дифференциальных уравнений, что несравнимо сложнее и дольше, чем алгебраические операции с комплексными числами.

4. В чем ключевое отличие векторной диаграммы от топографической?

Векторная диаграмма показывает *величины* (например, ток $\dot{I}_1$, падение напряжения $\dot{U}_{ab}$) и их взаимное расположение (фазовые сдвиги). Топографическая диаграмма показывает *потенциалы* узлов ($\dot{\phi}_a$, $\dot{\phi}_b$) как точки на плоскости относительно общего нуля. Вектор напряжения $\dot{U}_{ab}$ на топографической диаграмме — это вектор, соединяющий точки $\dot{\phi}_b$ и $\dot{\phi}_a$.

5. Что такое «опорный» или «базисный» узел?

Это точка в схеме, чей потенциал условно принимается равным нулю ($\dot{\phi} = 0$). В Примере 1 это точка ‘f’. Выбор опорного узла произволен, но обычно выбирают узел с наибольшим числом подключенных ветвей или «землю» схемы, чтобы упростить расчеты.

6. Почему в примере $\dot{E}_1 = (200 — j40)$ В, а $\dot{E}_2 = 100$ В?

Это исходные данные задачи. Они означают, что ЭДС $\dot{E}_2$ имеет амплитуду 100 В и ее фаза принята за ноль (вектор направлен вдоль вещественной оси). ЭДС $\dot{E}_1$ имеет как вещественную, так и мнимую составляющую, то есть она сдвинута по фазе относительно $\dot{E}_2$. Ее модуль (амплитуда) равен $\sqrt{200^2 + (-40)^2} \approx 204$ В, а фаза $\arctan(-40/200) \approx -11.3^\circ$.

7. Актуальны ли эти ручные расчеты и диаграммы в эпоху SPICE-симуляторов?

Абсолютно. Симулятор — это «черный ящик», который может выдать неверный результат, если модель составлена с ошибкой. Ручной расчет простых цепей и построение диаграмм развивают у инженера «чувство физики» процесса, позволяют быстро оценить порядок величин и проверить адекватность машинного моделирования.

Заключение

Символический (комплексный) метод является краеугольным камнем современной теории электрических цепей. Он предоставляет инженерам мощный и универсальный аппарат для анализа установившихся режимов в линейных цепях синусоидального тока.

Преобразуя интегрально-дифференциальные уравнения в алгебраические, этот метод позволяет применять для AC-цепей все известные подходы (законы Кирхгофа, методы контурных токов и узловых потенциалов) с простой заменой $R$ на $Z$. Визуальные инструменты, такие как векторные и топографические диаграммы, служат не только для качественной проверки расчетов, но и для глубокого понимания фазовых соотношений и распределения потенциалов в схеме. Владение этим методом является базовой компетенцией любого специалиста в области электротехники и энергетики.

Нормативные документы

При выполнении и оформлении электротехнических расчетов и схем следует руководствоваться действующими стандартами. (Item 7)

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий. (Устанавливает стандартизованную терминологию для всех областей электротехники).
ГОСТ 2.721-74 — Единая система конструкторской документации. Обозначения условные графические в схемах. Обозначения общего применения. (Регламентирует символы для R, L, C, источников ЭДС и т.д. на схемах).
ГОСТ 2.701-2008 — ЕСКД. Схемы. Виды и типы. Общие требования к выполнению. (Определяет правила оформления электрических схем, включая перечни элементов).
ГОСТ 2.105-95 — ЕСКД. Общие требования к текстовым документам. (Регламентирует оформление расчетно-пояснительных записок, если расчет является частью проекта).

Расчет разветвленной электрической цепи синусоидального тока комплексным методом