Расчет неразветвленной последовательной RLC-цепи

Содержание страницы

1. Теоретические основы и физика процессов
2. Векторная диаграмма напряжений
3. Треугольник сопротивлений
4. Мощность и энергетические процессы
5. Практический пример расчета
Сравнительный анализ и экспертное дополнение
Интересные факты об RLC-цепях
FAQ: Часто задаваемые вопросы
Заключение

Неразветвленная (последовательная) RLC-цепь — это фундаментальный элемент электротехники, состоящий из трех ключевых компонентов: резистора (R), катушки индуктивности (L) и конденсатора (C), соединенных последовательно. Это классическая колебательная система.

Краткая история: Изучение процессов в таких цепях началось в XIX веке. После изобретения Лейденской банки (прототип конденсатора) и открытия явления самоиндукции Майклом Фарадеем и Джозефом Генри, ученые столкнулись с необходимостью описывать сложные процессы в цепях переменного тока. Огромный вклад в упрощение расчетов таких цепей внес Чарльз Штейнмец, который ввел символический метод (метод комплексных амплитуд), превративший сложные дифференциальные уравнения в доступную алгебру, которую мы используем сегодня.

1. Теоретические основы и физика процессов

Неразветвленная электрическая цепь, составленная из реальных физических компонентов, для целей анализа представляется эквивалентной схемой замещения. Эта схема состоит из идеализированных элементов: активного сопротивления \( R \), индуктивности \( L \) и емкости \( C \), соединенных последовательно.

На схемах принято указывать положительные направления:

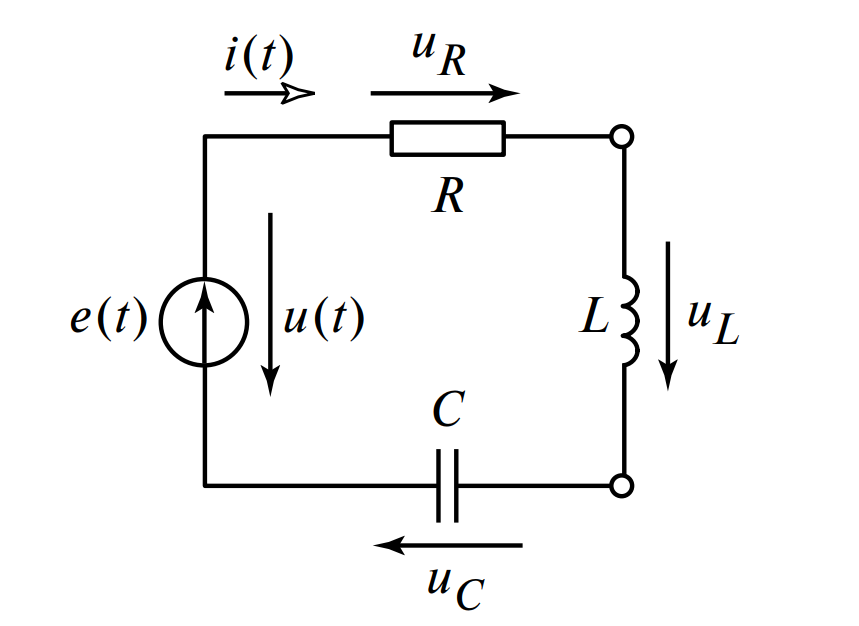
Мгновенных значений токов и напряжений (см. Рис. 1, а).
Действующих значений (см. Рис. 1, б).

Рис. 1. Схема последовательной RLC-цепи: а) для мгновенных значений; б) для действующих значений

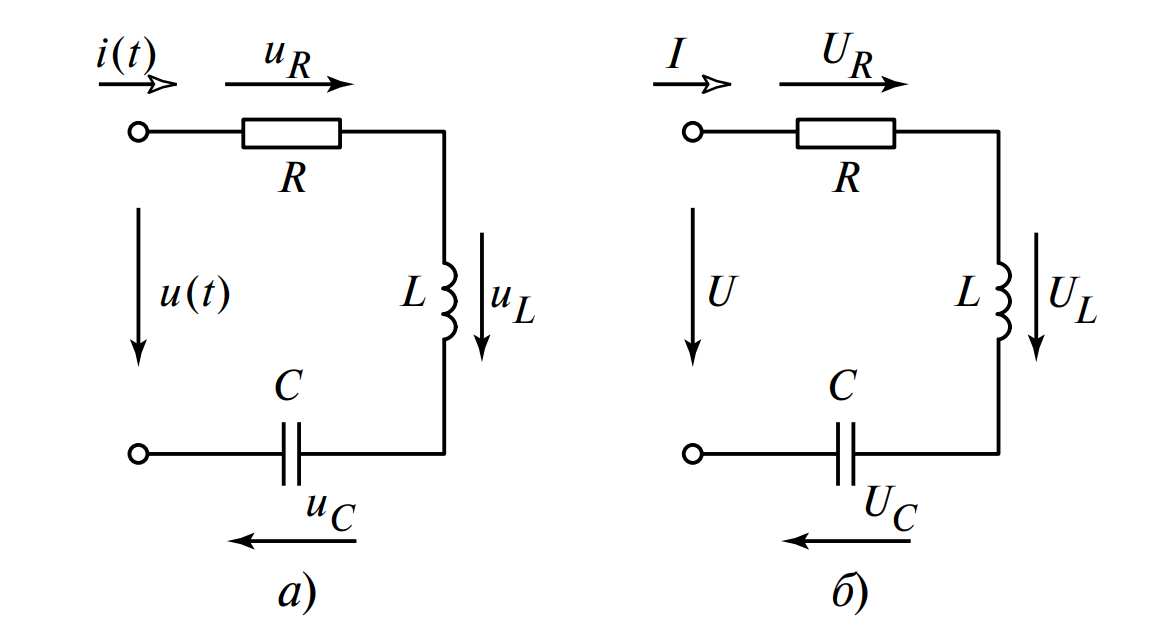
Согласно второму закону Кирхгофа, общее мгновенное напряжение источника \( u(t) \) равно сумме падений напряжений на каждом из последовательно соединенных участков:

\( u(t) = u_R + u_L + u_C \)

Учитывая физическую природу элементов, эти слагаемые определяются следующим образом:

Напряжение на резисторе: \( u_R = R \cdot i \)
Напряжение на индуктивности: \( u_L = L \frac{di}{dt} \)
Напряжение на емкости: \( u_C = \frac{1}{C} \int i(t) dt \)

Таким образом, поведение напряжения в зависимости от тока описывается интегродифференциальным уравнением:

u(t) = R \cdot i + L \frac{di}{dt} + \frac{1}{C} \int i(t) dt

Обратите внимание: Решение такого уравнения при произвольной форме тока — задача нетривиальная. Однако, если ток изменяется по гармоническому (синусоидальному) закону, процесс решения значительно упрощается.

Гармонический режим работы

Допустим, в цепи протекает синусоидальный ток вида \( i(t) = I_m \sin(\omega t) \). Для упрощения выкладок примем начальную фазу тока \( \psi_i \) равной нулю. Тогда мгновенные значения напряжений на элементах примут вид:

1. На резисторе: напряжение совпадает по фазе с током.
\( u_R = R \cdot I_m \sin(\omega t) = U_{Rm} \sin(\omega t) \)

2. На индуктивности: напряжение опережает ток на \( 90^\circ \) (\( \pi/2 \)).
\( u_L = L \frac{d(I_m \sin \omega t)}{dt} = \omega L I_m \cos(\omega t) = X_L I_m \sin(\omega t + \frac{\pi}{2}) = U_{Lm} \sin(\omega t + \frac{\pi}{2}) \)

3. На емкости: напряжение отстает от тока на \( 90^\circ \) (\( \pi/2 \)).
\( u_C = \frac{1}{C} \int I_m \sin(\omega t) dt = -\frac{1}{\omega C} I_m \cos(\omega t) = X_C I_m \sin(\omega t — \frac{\pi}{2}) = U_{Cm} \sin(\omega t — \frac{\pi}{2}) \)

Где введены реактивные сопротивления: \( X_L = \omega L \) (индуктивное) и \( X_C = \frac{1}{\omega C} \) (емкостное).

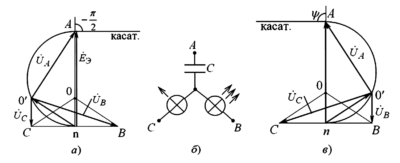
2. Векторная диаграмма напряжений

Использование действующих значений позволяет перейти к наглядному векторному представлению. Действующие значения напряжений определяются по закону Ома:

\( U_R = R \cdot I \)
\( U_L = X_L \cdot I \)
\( U_C = X_C \cdot I \)

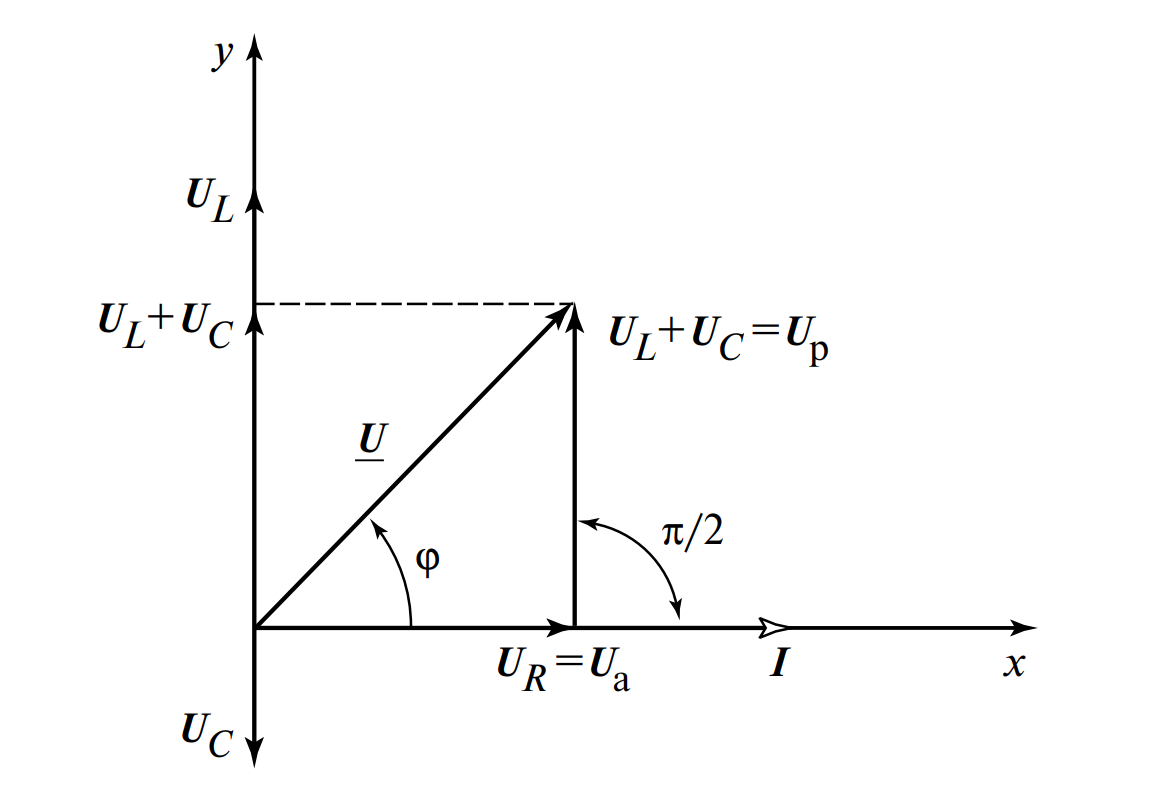
Рис. 2. Векторная диаграмма последовательной RLC-цепи

В векторной форме уравнение баланса напряжений выглядит так: \( \vec{U} = \vec{U}_R + \vec{U}_L + \vec{U}_C \).

Анализируя Рис. 2, можно заметить важную особенность: векторы \( \vec{U}_L \) и \( \vec{U}_C \) направлены вдоль одной прямой, но в противоположные стороны (находятся в противофазе). Их сумма образует реактивную составляющую напряжения \( \vec{U}_p \):

\vec{U}_L + \vec{U}_C = \vec{U}_p \), а по модулю \( U_p = |U_L — U_C|

Здесь \( U_p \) (реактивная составляющая) перпендикулярна вектору тока \( \vec{I} \), тогда как активная составляющая \( U_a \) (равная \( U_R \)) совпадает по направлению с током.

Векторы \( \vec{U} \), \( \vec{U}_a \) и \( \vec{U}_p \) формируют прямоугольный треугольник напряжений. Из теоремы Пифагора следует формула для действующего значения входного напряжения:

U = \sqrt{U_a^2 + U_p^2} = \sqrt{(RI)^2 + (X_L — X_C)^2 I^2} = I \sqrt{R^2 + (X_L — X_C)^2} = I \cdot Z

Где:

\( X = X_L — X_C \) — полное реактивное сопротивление цепи.
\( Z = \sqrt{R^2 + X^2} \) — полное сопротивление (импеданс) RLC-цепи.

Фазовый сдвиг

Угол сдвига фаз \( \phi \) между током и напряжением определяется геометрией треугольника напряжений:

\text{tg} \phi = \frac{U_p}{U_a} = \frac{U_L — U_C}{U_R} = \frac{X_L — X_C}{R}

От соотношения величин \( X_L \) и \( X_C \) зависит характер цепи (пределы угла \( -\frac{\pi}{2} \le \phi \le \frac{\pi}{2} \)):

Если \( X_L > X_C \) (т.е. \( X > 0, \phi > 0 \)) — цепь имеет активно-индуктивный характер.
Если \( X_L < X_C \) (т.е. \( X < 0, \phi < 0 \)) — цепь имеет активно-емкостный характер.

3. Треугольник сопротивлений

Поскольку все стороны треугольника напряжений пропорциональны току \( I \) (\( U_a = R I, U_p = X I, U = Z I \)), разделив их на ток, мы получаем подобный ему треугольник сопротивлений (см. Рис. 3).

Рис. 3. Треугольник сопротивлений R, X, Z

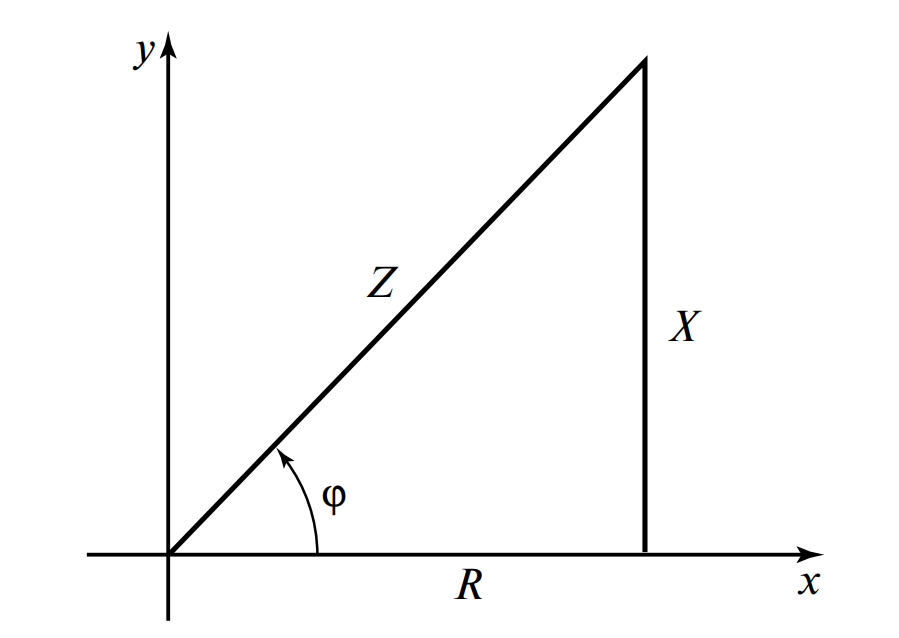
Из него следуют ключевые формулы расчета:

Z = \sqrt{R^2 + (X_L — X_C)^2} = \sqrt{R^2 + \left(\omega L — \frac{1}{\omega C}\right)^2}

\cos \phi = \frac{R}{Z}; \quad \sin \phi = \frac{X}{Z}; \quad \phi = \text{arctg} \frac{X_L — X_C}{R}

Мгновенное значение входного напряжения записывается как:
\( u(t) = U_m \sin(\omega t + \phi) \), где \( U_m = Z \cdot I_m \).

4. Мощность и энергетические процессы

Мгновенная мощность \( p(t) \) определяется произведением мгновенных значений напряжения и тока:

p(t) = u(t) i(t) = U_m I_m \sin(\omega t + \phi) \sin(\omega t) = U I \cos \phi — U I \cos(2\omega t + \phi)

Как видно из формулы и графиков на Рис. 4, мощность состоит из двух компонент:

1. Постоянной составляющей \( UI \cos \phi \).
2. Гармонической составляющей с удвоенной частотой \( 2\omega \).

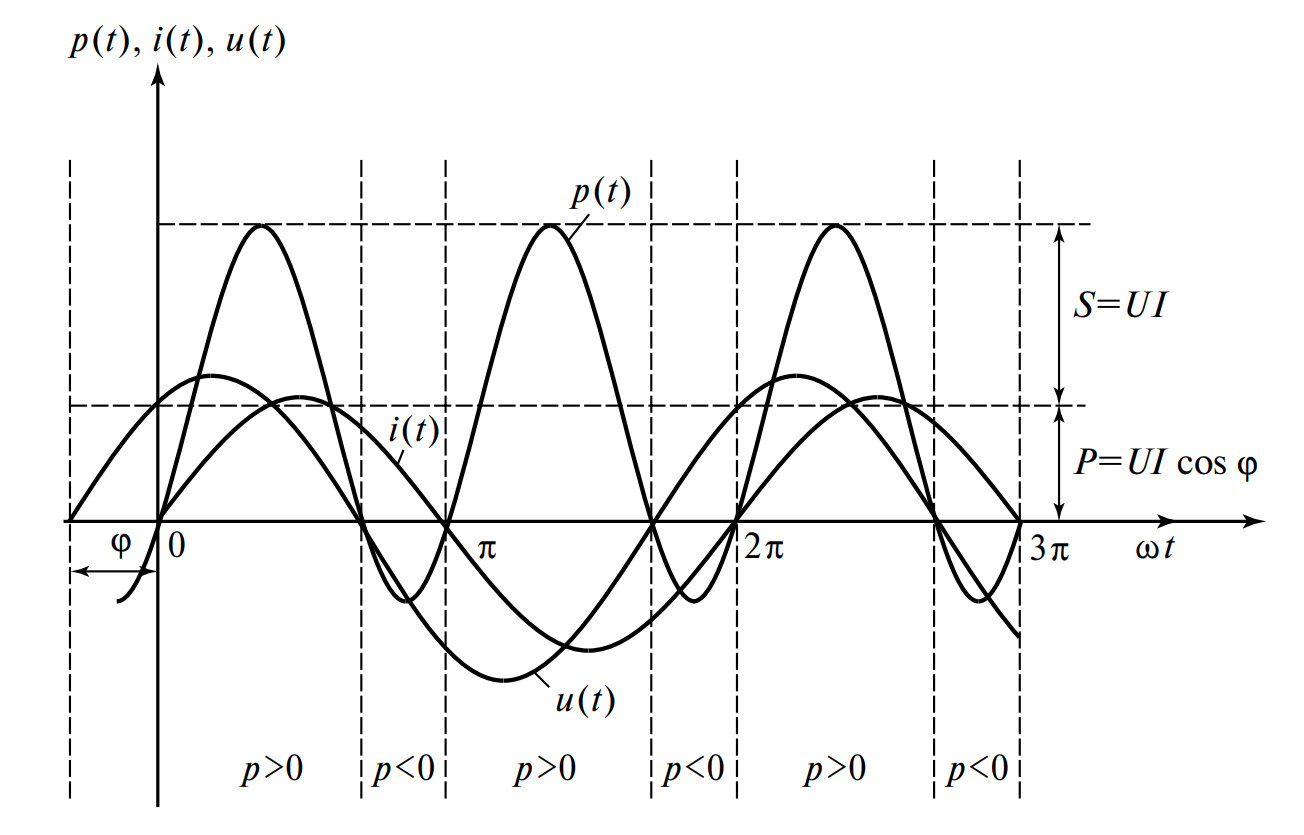
Рис. 4. Графики зависимостей u(t), i(t) и p(t) последовательной RLC-цепи

Среднее значение мощности за период равно постоянной составляющей. Это и есть активная мощность:

\( P = U I \cos \phi \) [Вт]

Важность коэффициента мощности:
Множитель \( \cos \phi \) называется коэффициентом мощности. Чем ближе угол \( \phi \) к нулю, тем ближе \( \cos \phi \) к единице, и тем эффективнее передается энергия от источника к потребителю. Повышение \( \cos \phi \) (компенсация реактивной мощности) — важнейшая задача в промышленной энергетике.

В однофазных цепях пульсация мощности с двойной частотой вызывает вибрации и гул электромеханического оборудования (трансформаторов, моторов).

Треугольник мощностей

По аналогии с напряжениями и сопротивлениями, существует треугольник мощностей (см. Рис. 5). Полная мощность \( S \) (измеряется в В·А) геометрически складывается из активной \( P \) и реактивной \( Q \) мощностей.

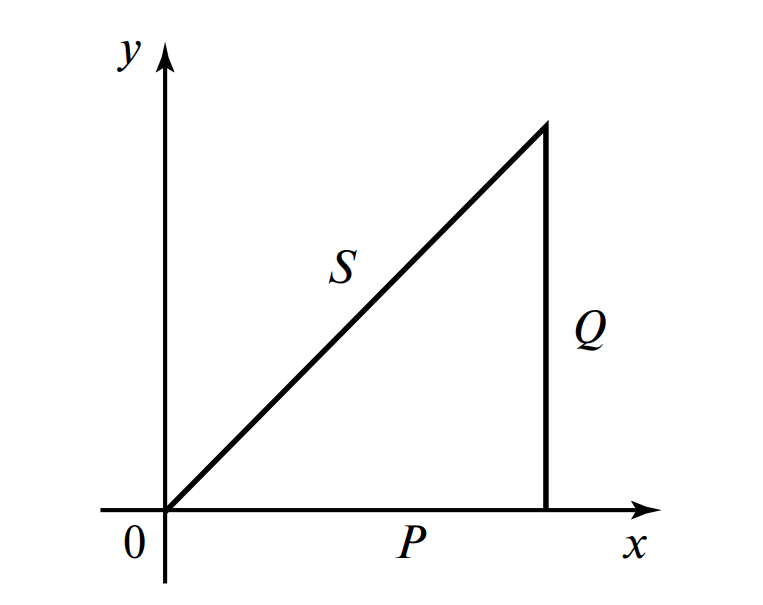
Рис. 5. Треугольник мощностей

\( S = U I = \sqrt{P^2 + Q^2} \) \( Q = U I \sin \phi \) [вар]

5. Практический пример расчета

Условие задачи (Пример 1): Последовательную RLC-цепь питает источник ЭДС \( e(t) = 200 \sin(1000t) \) В. Параметры элементов: \( R = 30 \) Ом, \( L = 0,01 \) Гн, \( C = 20 \) мкФ.

Необходимо: Определить характер цепи, найти функции \( i(t), u_R(t), u_L(t), u_C(t) \), рассчитать мощности и построить векторную диаграмму.

Рис. 6. Расчетная схема к примеру 1

Решение:

1. Подготовка данных.
Расчетная схема представлена на Рис. 6. Входное напряжение \( u(t) = e(t) \). Угловая частота \( \omega = 1000 \) рад/с.

2. Расчет сопротивлений.

Активное: \( R_a = R = 30 \) Ом.
Индуктивное: \( X_L = \omega L = 1000 \cdot 0,01 = 10 \) Ом.
Емкостное: \( X_C = \frac{1}{\omega C} = \frac{1}{1000 \cdot 20 \cdot 10^{-6}} = 50 \) Ом.
Реактивное: \( X = X_L — X_C = 10 — 50 = -40 \) Ом.
Полное (импеданс): \( Z = \sqrt{R^2 + X^2} = \sqrt{30^2 + (-40)^2} = \sqrt{900 + 1600} = 50 \) Ом.

3. Амплитуда тока.
\( I_m = \frac{E_m}{Z} = \frac{200}{50} = 4 \) А.

4. Характер цепи.
Так как \( X < 0 \) (\( X_C > X_L \)), цепь имеет активно-емкостный характер.

5. Фазовые соотношения.
Сдвиг фаз: \( \phi = \text{arctg}\left(\frac{X}{R}\right) = \text{arctg}\left(\frac{-40}{30}\right) \approx -53,13^\circ \).
Отрицательный знак означает, что напряжение отстает от тока (или ток опережает напряжение) на \( 53,13^\circ \).

6. Мгновенное значение тока.
\( i(t) = I_m \sin(\omega t — \phi) = 4 \sin(1000t — (-53,13^\circ)) = 4 \sin(1000t + 53,13^\circ) \) А.

7. Амплитуды напряжений.

\( U_{Rm} = I_m R = 4 \cdot 30 = 120 \) В.
\( U_{Lm} = I_m X_L = 4 \cdot 10 = 40 \) В.
\( U_{Cm} = I_m X_C = 4 \cdot 50 = 200 \) В.

8. Мгновенные значения напряжений.

\( u_R(t) \) совпадает по фазе с током:\( u_R = 120 \sin(1000t + 53,13^\circ) \) В.
\( u_L(t) \) опережает ток на \( 90^\circ \):\( u_L = 40 \sin(1000t + 53,13^\circ + 90^\circ) = 40 \sin(1000t + 143,13^\circ) \) В.
\( u_C(t) \) отстает от тока на \( 90^\circ \):\( u_C = 200 \sin(1000t + 53,13^\circ — 90^\circ) = 200 \sin(1000t — 36,86^\circ) \) В.

9. Расчет мощностей.

Коэффициент мощности: \( \cos \phi = \cos(-53,13^\circ) = 0,6 \).
Действующие значения: \( U = 200 / \sqrt{2} \approx 141.4 \) В, \( I = 4 / \sqrt{2} \approx 2.82 \) А. (Но для расчета мощности проще использовать амплитуды: \( P = \frac{1}{2} U_m I_m \cos \phi \) или через действующие, но здесь удобнее через сопротивление \( P = I^2 R \), где \( I \) — действующее. В примере из текста используется формула \( P = UI \cos \phi \) подразумевая действующие, но часто в учебных примерах берут амплитуды для оценки или специально оговаривают. Проверим по примеру: \( P = I^2 R \). Действующий ток \( I = 4/\sqrt{2} \). \( I^2 = 8 \). \( P = 8 \cdot 30 = 240 \) Вт. В исходном тексте \( 240 \) Вт. Все верно).
Активная мощность: \( P = 240 \) Вт.
Реактивная мощность: \( Q = I^2 X = 8 \cdot (-40) = -320 \) вар (или 320 вар, емкостная).
Полная мощность: \( S = \sqrt{P^2 + Q^2} = \sqrt{240^2 + 320^2} = 400 \) В·А.

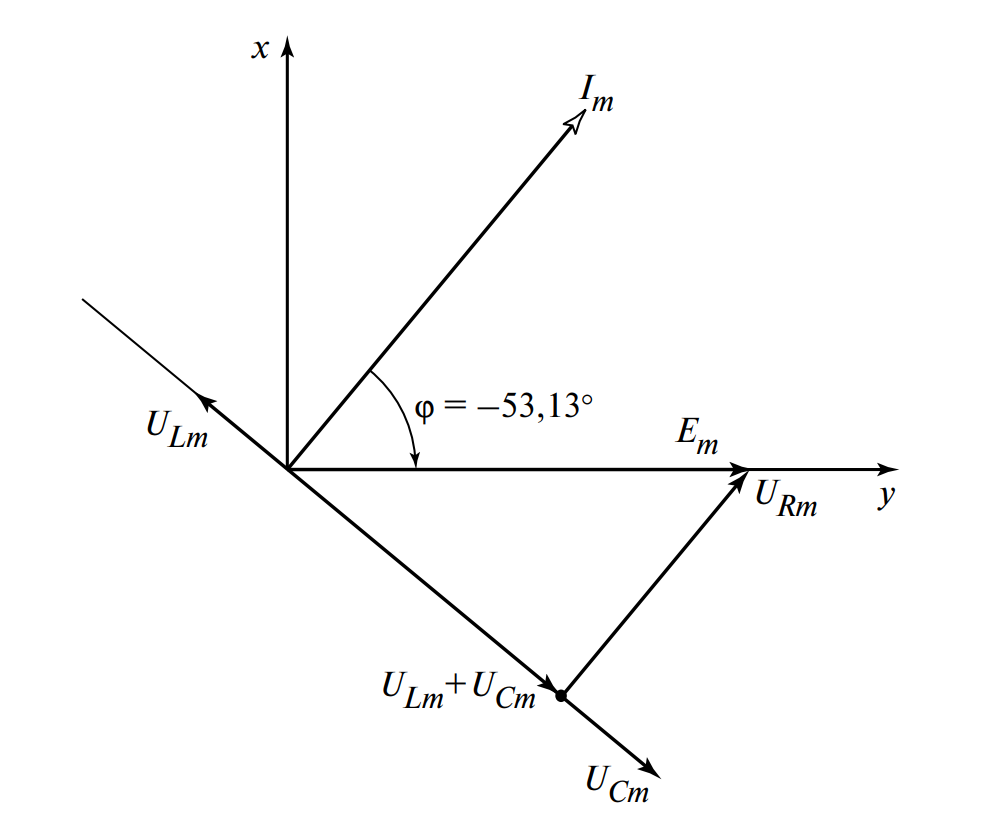
10. Векторная диаграмма.
Строится по рассчитанным значениям (см. Рис. 7).

Рис. 7. Векторная диаграмма для примера 1

Сравнительный анализ и экспертное дополнение

Таблица сравнения: Последовательная vs Параллельная RLC-цепь

Параметр	Последовательная RLC	Параллельная RLC
Общий параметр	Ток \( I \) (одинаков во всех элементах)	Напряжение \( U \) (одинаково на всех элементах)
Основной закон	II закон Кирхгофа (сумма напряжений)	I закон Кирхгофа (сумма токов)
Условие резонанса	\( X_L = X_C \) (Резонанс напряжений)	\( B_L = B_C \) (Резонанс токов)
Импеданс при резонансе	Минимальный (\( Z = R \))	Максимальный (\( Z \to \infty \) в идеале)
Опасность	Перенапряжения на L и C (\( U_L, U_C \gg U_{вх} \))	Сверхтоки в ветвях L и C (\( I_L, I_C \gg I_{общ} \))

Преимущества и недостатки последовательной схемы

Преимущества:

Простота анализа и реализации фильтров.
Возможность получения высоких напряжений (добротность) в радиотехнике для выделения сигнала.
Блокировка постоянной составляющей тока (благодаря конденсатору).

Недостатки:

При разрыве любого элемента цепь полностью размыкается.
Риск пробоя изоляции катушек или конденсаторов при резонансе напряжений.
Чувствительность к изменению частоты источника питания.

Интересные факты об RLC-цепях

Резонанс как катастрофа: Механический аналог электрического резонанса стал причиной разрушения Такомского моста. В электрике резонанс напряжений может мгновенно сжечь изоляцию кабеля, рассчитанного на 220В, подняв напряжение до киловольт.
Основа радиосвязи: Без RLC-контура не было бы радио. Вращая ручку настройки старого радиоприемника, вы меняли емкость конденсатора \( C \), настраивая контур в резонанс с частотой радиостанции.
Паразитные параметры: Идеальных R, L, C не существует. У любого реального резистора есть паразитная индуктивность и емкость, что на высоких частотах превращает его в сложную RLC-цепь.
Добротность (Q): Показывает, во сколько раз напряжение на реактивном элементе при резонансе превышает входное. В высококачественных контурах Q может достигать сотен и тысяч.
Компенсация реактива: На заводах ставят огромные шкафы с конденсаторами (C) последовательно или параллельно нагрузке (L — моторы), чтобы уменьшить угол \( \phi \) и не платить штрафы за реактивную энергию.
Биология: Мембрана нервной клетки моделируется как RLC-цепь, где липидный слой — это емкость, а ионные каналы — сопротивления.
Сверхпроводимость: В сверхпроводящих контурах \( R \to 0 \), колебания тока могут продолжаться практически вечно без подпитки извне.

FAQ: Часто задаваемые вопросы

Вопрос 1: Почему напряжение на катушке может быть больше напряжения розетки?

Это эффект резонанса. Энергия перекачивается между магнитным полем катушки и электрическим полем конденсатора. Если потери (R) малы, амплитуда этих «качелей» может многократно превысить амплитуду толчков (входного напряжения).

Вопрос 2: В чем физический смысл мнимой единицы \( j \) в расчетах?

Мнимая единица — это оператор поворота вектора на 90 градусов. В формулах она просто кодирует тот факт, что ток в конденсаторе и катушке сдвинут по фазе относительно напряжения на четверть периода.

Вопрос 3: Что такое «вар» в измерении мощности?

ВАР — Вольт-Ампер Реактивный. Это единица измерения мощности, которая не совершает полезной работы (не греет, не светит), а просто «гуляет» от источника к нагрузке и обратно, загружая провода.

Вопрос 4: Как практически измерить угол сдвига фаз?

Для этого используют осциллограф (по фигурам Лиссажу или временной развертке) или специальный прибор — фазометр.

Вопрос 5: Зависит ли сопротивление резистора R от частоты?

В теории — нет. Но на практике проявляется скин-эффект: на высоких частотах ток вытесняется к поверхности проводника, и его эффективное активное сопротивление растет.

Заключение

Расчет неразветвленной RLC-цепи — это базовый навык, необходимый любому инженеру-электрику. Понимание векторных диаграмм и треугольников мощностей позволяет не просто подставлять числа в формулы, а глубоко чувствовать физику процесса: как энергия циркулирует между элементами и как фазовые сдвиги влияют на эффективность системы. Освоив этот материал, вы сможете переходить к анализу более сложных, разветвленных цепей и трехфазных систем.

Нормативная база и литература

ГОСТ 2.702-2011 — Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем.
ГОСТ R 52002-2003 — Электротехника. Термины и определения основных понятий (современный аналог международных стандартов МЭК).
ГОСТ 2.728-74 — ЕСКД. Обозначения условные графические в схемах. Резисторы, конденсаторы.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2023.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — СПб.: Питер, 2019.