Расчет цепей синусоидального тока: Комплексный метод

Содержание страницы

1. Теоретические основы расчета сложных цепей
2. Практический пример расчета
3. Сравнение методов расчета
4. Преимущества и недостатки символического метода
5. Интересные факты о расчетах цепей
6. FAQ: Часто задаваемые вопросы
Заключение

Что это и зачем нужно? Данный материал описывает фундаментальный подход к расчету электрических цепей переменного тока (AC), имеющих сложную конфигурацию (топологию). Метод основан на переходе от дифференциальных уравнений во временной области к алгебраическим уравнениям в комплексной области.

Историческая справка: Революцию в электротехнике совершил Чарлз Протеус Штейнмец в конце XIX века. Именно он предложил использовать комплексные числа (символический метод) для описания цепей переменного тока. Это позволило инженерам рассчитывать сложные системы электроснабжения, используя простые алгебраические законы, аналогичные законам цепей постоянного тока, вместо сложного интегро-дифференциального исчисления.

1. Теоретические основы расчета сложных цепей

В общем случае электрическая цепь характеризуется сложной топологией. Это означает, что она может содержать произвольное количество активных (источники ЭДС и тока) и пассивных (резисторы, катушки, конденсаторы) элементов. Эти элементы располагаются в различных ветвях и включаются между различными узлами схемы.

Для описания структуры цепи используются следующие параметры:

\( b \) — число ветвей (исключая ветви, содержащие только идеальные источники тока).
\( y \) — число узлов.

Эти параметры определяют количество независимых контуров и, соответственно, количество уравнений состояния цепи, которые необходимо составить по первому и второму законам Кирхгофа. Для решения задачи используются методы контурных токов, узловых потенциалов и другие классические методы.

Количество необходимых уравнений: По первому закону Кирхгофа (и для метода узловых потенциалов): \[ k_I = y — 1 \] По второму закону Кирхгофа (и для метода контурных токов): \[ k_{II} = b — k_I = b — y + 1 \]

Принципы расчета базируются на тех же алгоритмах, что и для цепей постоянного тока (рассмотренных в классической теории), однако ключевым отличием является использование комплексной формы. Токи, напряжения, ЭДС и сопротивления входят в уравнения как комплексные числа (фазоры).

Аналогия для понимания:
Представьте цепь постоянного тока как систему труб, где вода течет с постоянной скоростью. Цепь синусоидального тока — это море, где вода колеблется (волны). Считать волны во времени сложно (нужно учитывать каждую секунду). Комплексный метод «замораживает» волну, позволяя нам оперировать только её высотой (амплитудой) и сдвигом относительно других волн (фазой), как если бы это были постоянные величины.

1.1. Подготовка данных для расчета

Рассмотрим алгоритм. Обычно задача анализа сводится к нахождению токов в ветвях по известным параметрам элементов. После нахождения токов можно вычислить напряжения между любыми точками.

Предположим, для цепи заданы мгновенные значения ЭДС и тока источника:

e_1(t) = E_{1m} \sin (\omega t + \psi_1) \] \[ e_2(t) = E_{2m} \sin (\omega t + \psi_2) \] \[ e_3(t) = E_{3m} \sin (\omega t + \psi_3) \] \[ J(t) = J_m \sin (\omega t + \psi)

Для применения символического (комплексного) метода необходимо перевести эти данные в комплексную форму (действующие значения):

Комплексные ЭДС и ток источника: \[ \underline{E}_1 = \frac{E_{1m}}{\sqrt{2}} \angle \psi_1; \quad \underline{E}_2 = \frac{E_{2m}}{\sqrt{2}} \angle \psi_2; \quad \underline{E}_3 = \frac{E_{3m}}{\sqrt{2}} \angle \psi_3 \] \[ \underline{J} = \frac{J_m}{\sqrt{2}} \angle \psi \]

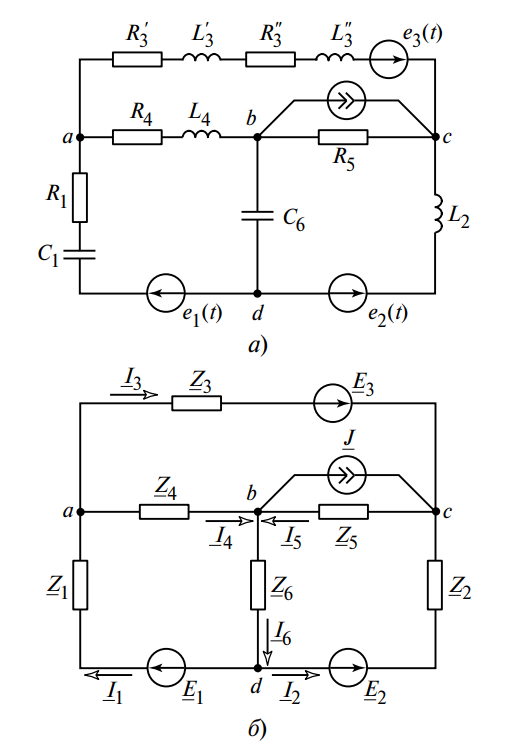
Комплексные сопротивления (импедансы) ветвей рассчитываются следующим образом (согласно рис. 1):

\underline{Z}_1 = R_1 — \frac{j}{\omega C_1} \] \[ \underline{Z}_2 = j\omega L_2 \] \[ \underline{Z}_3 = (R_3′ + R_3») + j\omega (L_3′ + L_3») \] \[ \underline{Z}_4 = R_4 + j\omega L_4 \] \[ \underline{Z}_5 = R_5 \] \[ \underline{Z}_6 = — \frac{j}{\omega C_6}

Рис. 1. Разветвленная цепь синусоидального тока (а) и её схема замещения (б)

1.2. Составление системы уравнений

Для записи уравнений необходимо произвольно выбрать условно-положительные направления токов в ветвях. В рассматриваемом примере (рис. 1) имеется \( b = 6 \) ветвей с неизвестными токами и \( y = 4 \) узла.

1. Уравнения по первому закону Кирхгофа:
Количество уравнений \( k_I = 4 — 1 = 3 \). Составляем их для всех узлов, кроме базисного (например, узла \( d \)).

Для узла \( a \): \( -\underline{I}_1 + \underline{I}_3 + \underline{I}_4 = 0 \)
Для узла \( b \): \( -\underline{I}_4 — \underline{I}_5 — \underline{I}_6 = \underline{J} \) (входящий ток источника)
Для узла \( c \): \( \underline{I}_5 — \underline{I}_3 — \underline{I}_2 = 0 \)

2. Уравнения по второму закону Кирхгофа:
Количество уравнений \( k_{II} = 6 — 4 + 1 = 3 \). Выбираем независимые контуры и направления их обхода:

Контур \( a-b-d-a \): \( \underline{Z}_4 \underline{I}_4 + \underline{Z}_6 \underline{I}_6 + \underline{Z}_1 \underline{I}_1 = \underline{E}_1 \)
Контур \( b-c-d-b \): \( -\underline{Z}_5 \underline{I}_5 — \underline{Z}_2 \underline{I}_2 — \underline{Z}_6 \underline{I}_6 = \underline{E}_2 \)
Контур \( a-c-b-a \): \( \underline{Z}_3 \underline{I}_3 — \underline{Z}_5 \underline{I}_5 + \underline{Z}_4 \underline{I}_4 = \underline{E}_3 \)

Важно! При составлении уравнений следите за знаками. Если направление обхода контура совпадает с направлением тока, падение напряжения берется со знаком «плюс», если нет — со знаком «минус». Аналогично для ЭДС.

Совместное решение полученной системы из шести уравнений позволяет найти шесть неизвестных токов (\( \underline{I}_1 \dots \underline{I}_6 \)).

2. Практический пример расчета

Рассмотрим конкретную задачу для закрепления материала.

Дано:
Ток в третьей ветви \( \underline{I}_3 = 5 \angle 0^\circ \) А.
Параметры элементов: \( R_1 = X_1 = X_3 = 10 \) Ом, \( R_2 = 6 \) Ом, \( X_2 = -8 \) Ом (емкостное).
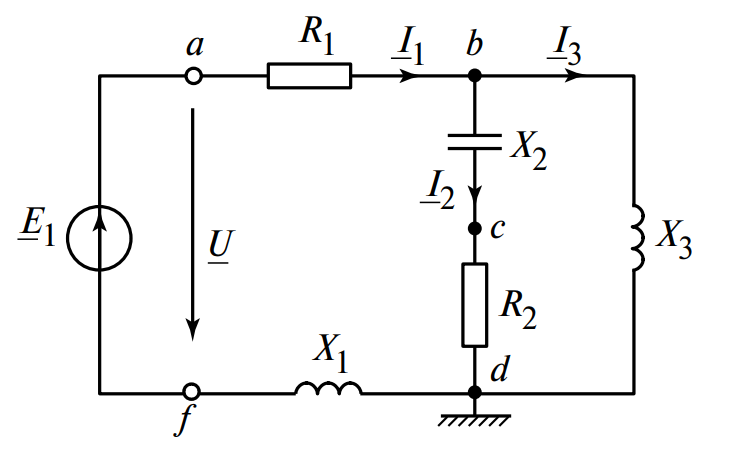
Схема соответствует рис. 2.

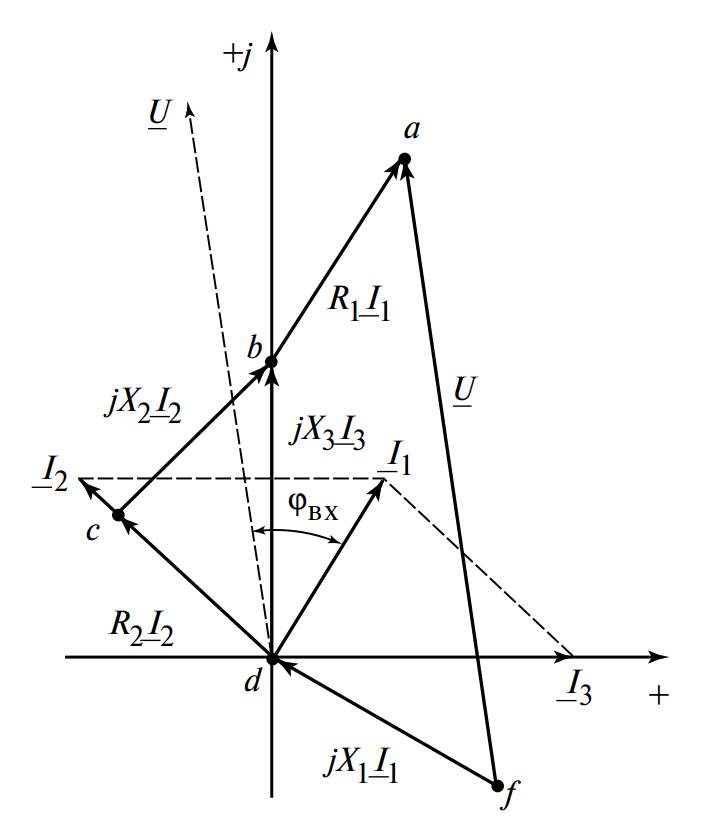
Задача: Построить векторную диаграмму и вычислить приложенное напряжение.

Рис. 2. Схема разветвленной цепи к примеру

Решение

Расчет выполняется последовательно, переходя от известных величин к неизвестным (метод раскручивания схемы с конца или пошаговый расчет потенциалов):

1. Примем потенциал узла \( d \) равным нулю: \( \underline{\phi}_d = 0 \). 2. Напряжение \( \underline{U}_{bd} \) (падение напряжения на индуктивности \( X_3 \)): \[ \underline{U}_{bd} = j X_3 \cdot \underline{I}_3 = j10 \cdot 5 = j50 \text{ В} \] 3. Ток \( \underline{I}_2 \) в ветви с \( R_2 \) и \( X_2 \). Так как ветвь параллельна напряжению \( \underline{U}_{bd} \): \[ \underline{I}_2 = \frac{\underline{U}_{bd}}{R_2 + j X_2} = \frac{j50}{6 — j8} \] Умножим числитель и знаменатель на сопряженное или переведем в показательную форму (\( 6-j8 = 10 \angle -53^\circ \)): \[ \underline{I}_2 = \frac{50 \angle 90^\circ}{10 \angle -53^\circ} = 5 \angle 143^\circ \text{ А} \] 4. Напряжение \( \underline{U}_{cd} \) (на резисторе \( R_2 \)): \[ \underline{U}_{cd} = R_2 \cdot \underline{I}_2 = 6 \cdot (5 \angle 143^\circ) = 30 \angle 143^\circ \text{ В} \] 5. Напряжение \( \underline{U}_{bc} \) (на емкости \( X_2 \)): \[ \underline{U}_{bc} = j X_2 \cdot \underline{I}_2 = (-j8) \cdot (5 \angle 143^\circ) = (8 \angle -90^\circ) \cdot (5 \angle 143^\circ) = 40 \angle 53^\circ \text{ В} \] 6. Ток \( \underline{I}_1 \) (общий ток). По первому закону Кирхгофа для узла, где сходятся токи (предположительно \( I_1 = I_2 + I_3 \)): \[ \underline{I}_1 = 5 \angle 143^\circ + 5 \angle 0^\circ = (-4 + j3) + 5 = 1 + j3 \] В показательной форме: \[ \underline{I}_1 = \sqrt{1^2 + 3^2} \angle \arctan(3/1) \approx 3,2 \angle 71,5^\circ \text{ А} \] 7. Напряжение на активном сопротивлении первой ветви \( \underline{U}_{R1} \): \[ \underline{U}_{R1} = R_1 \cdot \underline{I}_1 = 10 \cdot 3,2 \angle 71,5^\circ = 32 \angle 71,5^\circ \text{ В} \] 8. Напряжение на реактивном сопротивлении первой ветви \( \underline{U}_{X1} \): \[ \underline{U}_{X1} = j X_1 \cdot \underline{I}_1 = (10 \angle 90^\circ) \cdot (3,2 \angle 71,5^\circ) = 32 \angle 161,5^\circ \text{ В} \] 9. Общее приложенное напряжение \( \underline{U} \) (или ЭДС \( \underline{E}_1 \)): \[ \underline{U} = \underline{U}_{R1} + \underline{U}_{X1} + \underline{U}_{bd} \] Суммируя векторы (примерное значение из условия): \[ \underline{U} = -20 + j90 \approx 93 \angle 102^\circ \text{ В} \]

Рис. 3. Векторная диаграмма токов и напряжений

3. Сравнение методов расчета

Для более глубокого понимания сравним классический расчет во временной области с комплексным методом.

Критерий	Временная область (Мгновенные значения)	Комплексная область (Символический метод)
Математический аппарат	Дифференциальные и интегральные уравнения	Алгебраические уравнения с комплексными числами
Переменные	Функции времени \( i(t), u(t) \)	Комплексные амплитуды или действующие значения \( \underline{I}, \underline{U} \)
Сложность вычислений	Высокая (особенно для разветвленных цепей)	Средняя (сводится к операциям над матрицами или векторами)
Наглядность	Графики синусоид (осциллограммы)	Векторные диаграммы на комплексной плоскости

4. Преимущества и недостатки символического метода

Упрощение математики: Замена интегро-дифференциальных операций алгебраическими (умножение, деление, сложение).
Универсальность: Законы Ома и Кирхгофа записываются аналогично цепям постоянного тока.
Геометрическая интерпретация: Возможность построения векторных диаграмм для визуальной проверки правильности решения.

Ограничение по форме сигнала: Метод применим строго для синусоидальных токов одной частоты (для несинусоидальных требуется разложение в ряд Фурье).
Потеря физики процесса во времени: Результат не показывает переходные процессы, только установившийся режим.

5. Интересные факты о расчетах цепей

Символ j: Математики используют \( i \) для мнимой единицы, но электротехники используют \( j \), так как \( i \) уже занято для обозначения тока.
Вклад Эйлера: Формула Эйлера \( e^{jx} = \cos x + j \sin x \) — это «мост», соединяющий тригонометрию и комплексные числа, на котором держится вся теория цепей переменного тока.
Фазоры в энергетике: В современных энергосистемах используются устройства PMU (Phasor Measurement Units), которые измеряют комплексные фазоры напряжения и тока в реальном времени с точностью до микросекунд для предотвращения аварий.
Стандарт частоты: Расчеты импедансов \( Z_L = j\omega L \) и \( Z_C = 1/j\omega C \) напрямую зависят от частоты сети (50 Гц в СНГ/Европе или 60 Гц в США). При изменении частоты баланс цепи рушится.
Мощность — тоже комплексное число: Полная мощность \( S \) выражается как \( P + jQ \), где \( P \) — это полезная работа, а \( Q \) — энергия, бесполезно циркулирующая между источником и полями L и C.
Резонанс: Если в расчете мнимая часть общего сопротивления равна нулю, наступает резонанс. В этот момент напряжения на элементах могут в десятки раз превышать напряжение источника.
Матрицы: При большом количестве узлов (сотни и тысячи) для расчета используют матричный метод узловых потенциалов, который легко программируется на компьютере.

6. FAQ: Часто задаваемые вопросы

1. Можно ли использовать этот метод для токов разной частоты?

Нет, напрямую нельзя. Если в цепи действуют источники разных частот, применяется метод наложения: расчет проводится отдельно для каждой частоты, а результаты (мгновенные значения) суммируются.

2. Что такое «базисный узел» и как его выбрать?

Базисный узел — это узел, потенциал которого условно принимают равным нулю (заземляют). Выбирать можно любой узел, но обычно выбирают тот, где сходится больше всего ветвей, чтобы упростить уравнения.

3. В чем разница между \( Z \) и \( R \)?

\( R \) — это активное сопротивление (резистор), оно реально греется. \( Z \) — это полное комплексное сопротивление (импеданс), включающее как \( R \), так и реактивные части \( X_L, X_C \), которые не потребляют энергию безвозвратно, а запасают её.

4. Почему в формуле для \( Z_C \) стоит минус?

Импеданс конденсатора \( \frac{1}{j\omega C} = \frac{-j}{\omega C} \). Минус указывает на то, что ток в конденсаторе опережает напряжение на 90 градусов.

5. Что делать, если в ответе получился отрицательный угол, например \( 5 \angle -30^\circ \)?

Это нормально. Отрицательный угол означает отставание фазы синусоиды от начальной точки отсчета. Геометрически вектор просто повернут по часовой стрелке.

Заключение

Символический метод расчета цепей синусоидального тока является мощнейшим инструментом электротехники. Позволяя свести сложные дифференциальные задачи к алгебре комплексных чисел, он делает доступным анализ даже самых разветвленных электрических сетей. Понимание этого метода — ключевой навык для любого студента-энергетика или инженера, так как он лежит в основе проектирования всех современных систем электроснабжения.

Нормативная база

При оформлении технической документации и расчетов необходимо руководствоваться следующими стандартами:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Устанавливает корректную терминологию (активная, реактивная мощность, импеданс и т.д.).
ГОСТ 2.702-2011 «Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем». Регламентирует графические обозначения элементов на рисунках 1 и 2.
ГОСТ 1494-77 «Электротехника. Буквенные обозначения основных величин». Определяет использование символов \( I, U, Z, R, X \).

Список литературы

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2016.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — СПб.: Питер, 2003.
Зевеке Г.В., Ионкин П.А. Основы теории цепей. — М.: Энергия, 1975.