Расчет линейных цепей с негармоническими ЭДС и токами

Содержание страницы

Общая методология расчета
Применение принципа наложения
Особенности расчета для разных гармоник
Влияние реактивных элементов на форму тока
Сравнительная таблица влияния элементов на гармоники
Интересные факты по теме
FAQ: Часто задаваемые вопросы
Заключение

Расчет цепей с негармоническими (несинусоидальными) периодическими ЭДС и токами — это основной метод анализа линейных электрических цепей, в которых действуют источники, генерирующие сигналы, отличающиеся по форме от идеальной синусоиды. Несмотря на то, что они несинусоидальные, эти сигналы являются периодическими, то есть их форма повторяется через определенный интервал времени (период).

Такие сигналы повсеместно встречаются в современной электротехнике и электронике, например, в цепях с выпрямителями, тиристорными преобразователями, импульсными источниками питания и любыми нелинейными нагрузками, которые искажают форму потребляемого тока. Анализ таких цепей необходим для оценки качества электроэнергии, расчета потерь и проектирования фильтрующих устройств.

Теоретической основой для анализа таких цепей служит ряд Фурье. В начале XIX века французский математик Жан-Батист Жозеф Фурье разработал математический аппарат, доказывающий, что любую периодическую функцию (удовлетворяющую условиям Дирихле, что в электротехнике почти всегда выполняется) можно представить в виде суммы постоянной составляющей и бесконечного числа синусоидальных колебаний (гармоник).

Эти синусоидальные компоненты имеют частоты, кратные основной (первой) гармонике, частота которой равна частоте исходного несинусоидального сигнала. Этот математический аппарат позволил свести сложную задачу расчета цепи с сигналом произвольной формы к набору более простых задач — расчетам той же цепи, но с обычными синусоидальными и постоянными источниками.

Общая методология расчета

Ключевым условием для применения данного метода является линейность электрической цепи. Только в линейных цепях (состоящих из идеализированных R, L и C элементов, чьи параметры не зависят от тока или напряжения) справедлив принцип наложения (суперпозиции), который лежит в основе всего расчета.

Весь процесс анализа цепи с несинусоидальными источниками разбивается на три последовательных этапа:

Аналитический этап (Разложение в ряд Фурье): Все несинусоидальные периодические ЭДС и токи источников раскладываются в ряд Фурье. В результате исходный сложный сигнал $f(t)$ представляется в виде суммы:
- Постоянной составляющей (гармоника нулевого порядка, $F_0$).
- Основной (первой) гармоники ($f_1(t)$), имеющей ту же частоту, что и исходный сигнал.
- Высших гармоник ($f_k(t)$), частоты которых ($\omega_k$) кратно ($k=2, 3, 4, \dots$) превышают частоту основной гармоники ($\omega_1$).
Совокупность амплитуд и начальных фаз этих составляющих называется дискретным спектром сигнала.
Расчетный этап (Принцип наложения): Используя принцип наложения, производят расчет цепи для каждой гармоники по отдельности. Цепь рассчитывается столько раз, сколько значимых гармоник в спектре:
- Сначала для источника постоянного тока (все индуктивности заменяются коротким замыканием, емкости — разрывом).
- Затем для источника первой гармоники (расчет ведется стандартным комплексным методом для частоты $\omega_1$).
- Далее для источника второй гармоники (расчет для частоты $\omega_2 = 2\omega_1$) и т.д. для всех $k$-х гармоник.
Синтезирующий этап (Суммирование): Определяются результирующие токи и напряжения в ветвях. Мгновенное значение искомой величины (например, тока $i(t)$) в любой момент времени равно алгебраической сумме мгновенных значений, создаваемых каждой из гармоник (включая постоянную составляющую).

Примечание: На практике полное суммирование мгновенных значений (этап 3) для получения итоговой формы кривой выполняется не всегда. Часто для инженерных задач достаточно проанализировать дискретный спектр (этап 1) и рассчитать токи/напряжения для нескольких первых, наиболее значимых гармоник (этап 2). Это позволяет оценить искажения, рассчитать действующие значения и мощности, что является основной целью анализа.

Применение принципа наложения

Рассмотрим детально второй, ключевой этап расчета. Если несинусоидальная ЭДС $e(t)$ представлена в виде ряда Фурье (для примера ограничимся двумя гармониками и постоянной составляющей):

$$ e(t) = e_0 + e_1(t) + e_2(t) = E_0 + E_{1m}\sin(\omega_1 t + \psi_1) + E_{2m}\sin(\omega_2 t + \psi_2) $$

…то источник такой сложной ЭДС можно рассматривать как эквивалентную схему из последовательно соединенных нескольких идеализированных источников (см. Рисунок 1):

Источника постоянной ЭДС $e_0 = E_0$.
Источника синусоидальной ЭДС первой гармоники $e_1(t) = E_{1m}\sin(\omega_1 t + \psi_1)$.
Источника синусоидальной ЭДС второй гармоники $e_2(t) = E_{2m}\sin(\omega_2 t + \psi_2)$.

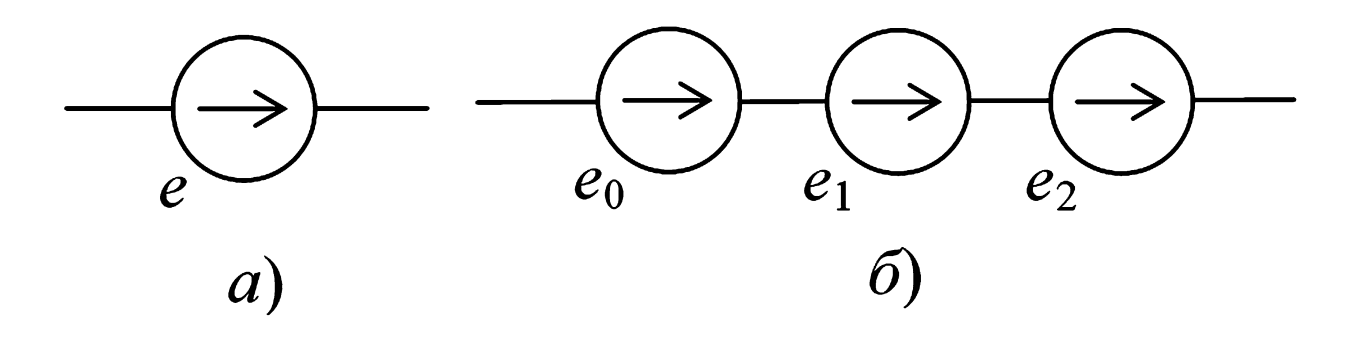
Рисунок 1. Эквивалентная замена негармонической ЭДС (а) суммой гармонических составляющих (б) для применения принципа наложения.

Применяя принцип наложения, мы поочередно рассчитываем токи в цепи от каждого источника, при этом все остальные источники ЭДС закорачиваются (источники тока разрываются). Рассматривая действие каждой составляющей ЭДС в отдельности, мы находим соответствующие составляющие токов во всех участках цепи.

Например, если в какой-либо ветви ток от ЭДС $E_0$ равен $I_0$, ток от $e_1(t)$ равен $i_1(t)$, а ток от $e_2(t)$ равен $i_2(t)$, то результирующий мгновенный ток $i(t)$ в этой ветви будет равен их сумме:

$$ i(t) = I_0 + i_1(t) + i_2(t) $$

Таким образом, одна сложная задача расчета цепи с негармонической ЭДС сводится к $n+1$ простым задачам, где $n$ — число учитываемых синусоидальных гармоник, и одна задача — для постоянного тока.

Особенности расчета для разных гармоник

Критически важной особенностью расчета является то, что параметры реактивных элементов цепи (индуктивностей и емкостей) зависят от частоты. Следовательно, для каждой гармоники их сопротивления будут разными, что коренным образом влияет на прохождение токов этих гармоник.

Зависимость реактивных сопротивлений

Пусть $k$ — это номер гармоники (для основной $k=1$, для второй $k=2$ и т.д.). Тогда угловая частота $k$-й гармоники равна $\omega_k = k\omega_1$.

Индуктивное сопротивление $x_L$ для $k$-й гармоники:

$$ x_{Lk} = \omega_k L = (k\omega_1)L = k( \omega_1 L) = k \cdot x_{L1} $$

Это означает, что индуктивное сопротивление прямо пропорционально номеру гармоники. Для высших гармоник индуктивность представляет собой большее сопротивление, чем для основной.

Емкостное сопротивление $x_C$ для $k$-й гармоники:

$$ x_{Ck} = \frac{1}{\omega_k C} = \frac{1}{(k\omega_1)C} = \frac{1}{k} \left( \frac{1}{\omega_1 C} \right) = \frac{x_{C1}}{k} $$

Емкостное сопротивление, наоборот, обратно пропорционально номеру гармоники. Для высших гармоник емкость представляет меньшее сопротивление.

Зависимость активного сопротивления (Скин-эффект)

Активное сопротивление $R$ проводника также зависит от частоты из-за поверхностного эффекта (скин-эффекта). С ростом частоты переменный ток вытесняется к поверхности проводника, уменьшая эффективное сечение и увеличивая тем самым активное сопротивление.

При расчетах на промышленных (50/60 Гц) и относительно низких частотах (до нескольких килогерц) и для проводов малого сечения этим эффектом часто пренебрегают. В таких случаях считают, что активное сопротивление для всех гармоник равно сопротивлению на постоянном токе ($R_k \approx R_0$). Однако в высокочастотных цепях или при расчете мощных кабельных линий, учет скин-эффекта и эффекта близости обязателен для точного определения потерь.

Влияние реактивных элементов на форму тока

Различная зависимость $x_L$ и $x_C$ от частоты приводит к тому, что эти элементы по-разному влияют на высшие гармоники, выступая в роли естественных частотных фильтров.

Поведение емкости (C)

Представим, что к зажимам конденсатора C приложено несинусоидальное напряжение. Для $k$-й гармоники напряжения $u_k(t) = E_{km}\sin(\omega_k t + \psi_k)$, емкостное сопротивление равно $x_{Ck} = 1/(k\omega_1 C)$. Мгновенный ток $k$-й гармоники будет (опережая напряжение на 90° или $\pi/2$):

$$ i_k(t) = \frac{E_{km}}{x_{Ck}} \sin(\omega_k t + \psi_k + \frac{\pi}{2}) = E_{km} \cdot k\omega_1 C \cdot \sin(\omega_k t + \psi_k + \frac{\pi}{2}) $$

Обратите внимание, что амплитуда тока $I_{km} = E_{km} / x_{Ck}$ пропорциональна номеру гармоники $k$.

Вывод: Емкость «облегчает» прохождение высших гармоник тока. Даже если амплитуда высшей гармоники напряжения ($E_{km}$) мала по сравнению с основной, результирующий ток $k$-й гармоники ($I_{km}$) может быть соизмерим или даже превышать ток основной гармоники. Поэтому ток через емкость всегда более несинусоидален (более искажен), чем напряжение на ней.

Поведение индуктивности (L)

Теперь подключим к тому же напряжению катушку индуктивности L. Индуктивное сопротивление равно $x_{Lk} = k\omega_1 L$. Мгновенный ток $k$-й гармоники будет (отставая от напряжения на 90° или $\pi/2$):

$$ i_k(t) = \frac{E_{km}}{x_{Lk}} \sin(\omega_k t + \psi_k — \frac{\pi}{2}) = \frac{E_{km}}{k\omega_1 L} \sin(\omega_k t + \psi_k — \frac{\pi}{2}) $$

В этом случае амплитуда тока $I_{km} = E_{km} / x_{Lk}$ обратно пропорциональна номеру гармоники $k$.

Вывод: Индуктивность «препятствует» прохождению высших гармоник тока. Она активно подавляет высокочастотные составляющие. Поэтому ток через индуктивность всегда более синусоидален (менее искажен), чем напряжение на ее зажимах. Индуктивность выполняет роль сглаживающего фильтра.

Сравнительная таблица влияния элементов на гармоники

Поведение пассивных элементов (R, L, C) в цепях несинусоидального тока является ключом к пониманию фильтрации и искажений. Ниже приведена сравнительная таблица их свойств.

Параметр	Активное сопротивление (R)	Индуктивность (L)	Емкость (C)
Зависимость сопротивления от частоты (гармоники $k$)	$R_k \approx R_0$ (слабо зависит, не считая скин-эффекта)	$x_{Lk} = k \cdot x_{L1}$ (прямо пропорциональна)	$x_{Ck} = x_{C1} / k$ (обратно пропорциональна)
Влияние на высшие гармоники тока	Пропускает пропорционально напряжению ($I_k \sim E_k$)	Подавляет (ослабляет) ($I_k \sim E_k / k$)	Усиливает (облегчает прохождение) ($I_k \sim E_k \cdot k$)
Влияние на форму тока (при несин. напряжении)	Форма тока повторяет форму напряжения	Ток сглаживается (становится более синусоидальным)	Ток искажается (становится более несинусоидальным)
Основная роль в цепи	Рассеивание активной мощности	Сглаживающий фильтр, ограничитель ВЧ-составляющих	Проводник для ВЧ-составляющих, блокиратор постоянного тока

Преимущества и недостатки метода

Как и любой инженерный подход, метод разложения в ряд Фурье с последующим применением принципа наложения имеет свои сильные и слабые стороны.

Преимущества

Универсальность: Позволяет свести анализ любой сложной периодической формы к стандартным методам расчета цепей переменного (синусоидального) и постоянного тока.
Наглядность: Анализ спектра (амплитуд гармоник) сразу показывает, какие частоты вносят наибольший вклад, что неоценимо для проектирования фильтров.
Расчет мощности: Позволяет легко рассчитать активную, реактивную и полную мощности в цепи, используя сумму мощностей от каждой гармоники (согласно теореме Парсеваля).

Недостатки

Только для линейных цепей: Метод категорически неприменим, если в цепи есть нелинейные элементы (например, диоды, транзисторы в ключевом режиме), так как для них не работает принцип наложения.
Трудоемкость: Расчет требует (n+1) итераций, где ‘n’ — число гармоник. При ручном счете это долго; на практике учитывают лишь несколько первых гармоник, что вносит погрешность.
Только периодические сигналы: Метод в его классическом виде не работает для непериодических (случайных или одиночных) сигналов. Для них используется преобразование Фурье (интеграл Фурье), что является отдельной темой.

Интересные факты по теме

Симметрия упрощает: Если несинусоидальный сигнал обладает определенным типом симметрии (например, нечетной), в его ряде Фурье будут отсутствовать все четные гармоники и постоянная составляющая. Это сильно упрощает расчеты.
Коэффициент искажения (THD): Существует специальный параметр — Коэффициент несинусоидальности (Total Harmonic Distortion), который численно показывает, насколько форма сигнала отличается от синусоиды. Он строго регламентируется стандартами качества электроэнергии, например, ГОСТ 32144-2013.
Проблема третьей гармоники: В трехфазных системах с нулевым проводом гармоники, кратные трем (3, 9, 15…), ведут себя иначе, чем остальные. Они совпадают по фазе во всех трех фазах и не компенсируют друг друга в нулевом проводе, а складываются. Это может привести к опасной перегрузке нулевого проводника.
Резонанс на гармониках: В цепи, содержащей L и C, может возникнуть резонанс. Если резонансная частота цепи ($f_0 = 1 / (2\pi\sqrt{LC})$) случайно совпадет с частотой одной из высших гармоник, это вызовет резкое увеличение тока или напряжения этой гармоники, что может привести к повреждению оборудования.
Активная мощность: Активная мощность в цепи с несинусоидальным током равна сумме активных мощностей, развиваемых каждой гармоникой в отдельности. Мощность от взаимодействия тока одной гармоники с напряжением другой гармоники равна нулю.
«Музыкальные» гармоники: Понятие гармоник в электротехнике полностью аналогично музыкальным обертонам. Основная гармоника — это основной тон, а высшие гармоники (обертоны) определяют «тембр» электрического сигнала.
От Фурье к БПФ: Ручной расчет коэффициентов ряда Фурье сложен. С появлением компьютеров был разработан алгоритм Быстрого Преобразования Фурье (БПФ, FFT), который позволяет получить спектр сигнала практически мгновенно и лежит в основе всех современных цифровых анализаторов спектра.

FAQ: Часто задаваемые вопросы

1. Что такое «линейная цепь» и почему это важно?

Линейная цепь — это цепь, параметры элементов которой (R, L, C) не зависят от протекающего через них тока или приложенного напряжения. Это важно, потому что только для таких цепей справедлив принцип наложения, который является основой всего рассматриваемого метода. Если в цепи есть, например, диод, его сопротивление меняется в зависимости от напряжения, цепь нелинейна, и этот метод применять нельзя.

2. Что такое «постоянная составляющая» и как ее рассчитать?

Постоянная составляющая (или гармоника нулевого порядка, $E_0$ или $I_0$) — это среднее значение несинусоидального сигнала за один период. При расчете цепи на постоянном токе ($k=0$, $\omega=0$), все индуктивности $x_L=0$ (считаются коротким замыканием), а все емкости $x_C=\infty$ (считаются разрывом цепи).

3. Почему в тексте говорится, что индуктивность «сглаживает» ток?

Индуктивное сопротивление $x_{Lk} = k \cdot \omega_1 L$ растет с увеличением частоты (номера гармоники $k$). Это означает, что катушка индуктивности сильно сопротивляется «быстрым» изменениям тока (высшим гармоникам), но слабо — «медленным» (низшим гармоникам). В результате высокочастотные «рябь» и «иглы» в токе подавляются, и форма тока становится более плавной, приближенной к синусоиде.

4. А почему емкость, наоборот, «искажает» ток?

Емкостное сопротивление $x_{Ck} = 1 / (k \cdot \omega_1 C)$ уменьшается с ростом частоты. Емкость представляет малое сопротивление для высших гармоник. Если в напряжении есть даже небольшие высокочастотные составляющие, они создадут в емкости очень большие токи этих гармоник. Эти большие токи, суммируясь с током основной гармоники, и создают итоговую, сильно искаженную (несинусоидальную) форму тока.

5. Сколько гармоник нужно учитывать для точного расчета?

Это зависит от требуемой точности и формы сигнала. Для сигналов, близких к синусоиде (например, в сетях с небольшими искажениями), достаточно 3-5 гармоник. Для сигналов с резкими фронтами (например, прямоугольный импульс, «меандр») для точного описания формы могут потребоваться десятки или даже сотни гармоник. На практике для задач качества электроэнергии часто ограничиваются 25-й или 50-й гармоникой, согласно ГОСТ 32144-2013.

6. Можно ли использовать комплексный метод для расчета каждой гармоники?

Да, и это стандартный подход. Для каждой $k$-й гармоники цепь рассчитывается комплексным методом для ее собственной частоты $\omega_k$. Комплексное сопротивление индуктивности будет $ \dot{Z}_L = j x_{Lk} = j k\omega_1 L $, а емкости $ \dot{Z}_C = -j x_{Ck} = -j / (k\omega_1 C) $. После нахождения комплексных значений токов и напряжений их переводят обратно во временную (мгновенную) форму и суммируют.

7. Как найти действующее значение несинусоидального тока?

Действующее значение (RMS) несинусоидального сигнала — это корень квадратный из суммы квадратов действующих значений всех его гармоник (включая постоянную составляющую).

$$ I_{RMS} = \sqrt{I_0^2 + I_1^2 + I_2^2 + \dots + I_k^2} $$

Где $I_0$ — постоянная составляющая, а $I_1, I_2, \dots I_k$ — действующие значения 1-й, 2-й и k-й гармоник (равны амплитудным $I_{km} / \sqrt{2}$). Простое сложение действующих значений ($I_1+I_2+…$) является грубой ошибкой.

Заключение

Расчет цепей с негармоническими периодическими сигналами является неотъемлемой частью современной электротехники. Метод, основанный на разложении сигнала в ряд Фурье и применении принципа наложения, позволяет анализировать сложные процессы, используя хорошо освоенный аппарат расчета цепей постоянного и синусоидального тока.

Главный практический вывод из анализа заключается в частотно-зависимом поведении реактивных элементов: индуктивность выступает в роли фильтра, сглаживающего ток и подавляющего высшие гармоники, в то время как емкость, наоборот, представляет путь с низким сопротивлением для высших гармоник, что может приводить к значительному искажению формы тока. Понимание этих процессов критически важно для проектирования фильтров, оценки качества электроэнергии и обеспечения электромагнитной совместимости устройств.

Нормативные документы

ГОСТ 32144-2013 — «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения».
ГОСТ Р 52002-2003 — «Электротехника. Основные понятия. Словарь».

Расчет цепей с негармоническими периодическими ЭДС и токами: метод, формулы, анализ