Содержание страницы
Соединения элементов в электрической цепи — это фундаментальные способы их физического и схемотехнического объединения для создания функционального устройства. Три вида, на которых держится вся схемотехника, — это последовательное, параллельное и смешанное (комбинированное) соединения.
Компоненты любой электрической схемы, в частности пассивные элементы, такие как резисторы, могут быть соединены множеством различных способов. Однако в инженерной практике и теоретических расчетах фундаментальное значение имеют три основных метода коммутации, которые являются основой для построения всех остальных, более сложных схем.
1. Базовые типы соединений
Рассмотрим ключевые характеристики каждого типа соединения, используя в качестве примера резистивные элементы.
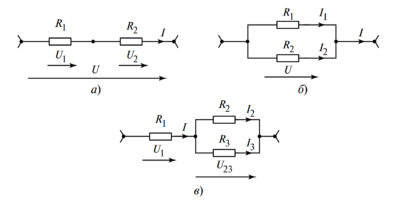
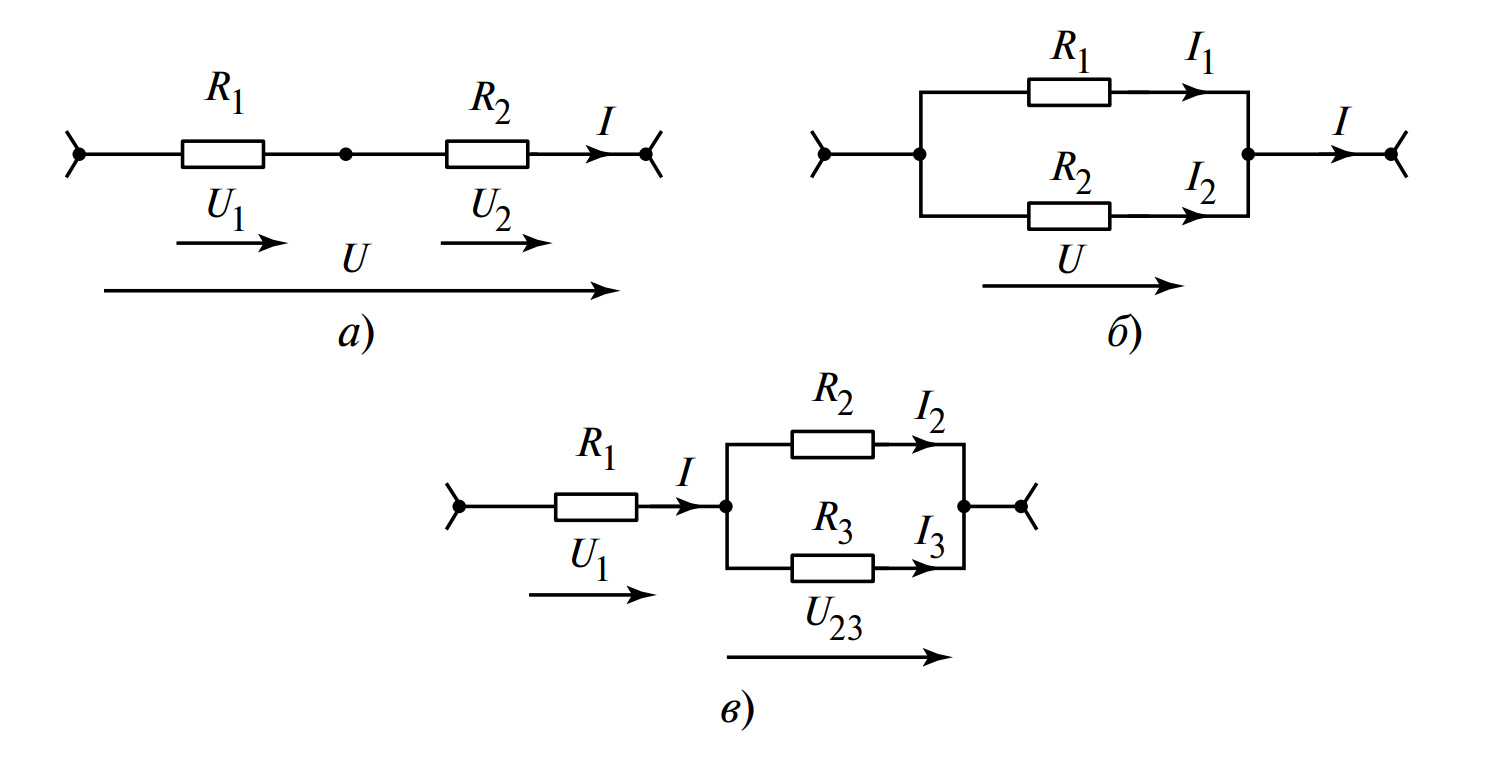
Рисунок 1. Основные способы соединения резистивных элементов:
а — последовательное соединение (ток \(I\) одинаков); б — параллельное соединение (напряжение \(U\) одинаково); в — смешанное соединение
1.1. Последовательное соединение
Последовательное соединение — это такое включение, при котором элементы схемы подключаются друг за другом, образуя единый, неразветвленный путь для тока. При этом конечный вывод (полюс, зажим) одного элемента соединяется с начальным выводом (полюсом, зажимом) следующего. Наглядный пример представлен на (рис. 1, а).
Ключевой физический закон для последовательного соединения: сила тока \(I\) одинакова во всех без исключения элементах этой цепи.
\(I_{общ} = I_1 = I_2 = … = I_n\)
Общее напряжение цепи при этом равно сумме падений напряжений на каждом элементе:
\(U_{общ} = U_1 + U_2 + … + U_n\)
Термин «последовательное соединение» также корректно применяется для описания соединения источников ЭДС (например, батареек в фонарике) или при последовательном включении источников с пассивными элементами (резисторами, лампами).
Преимущества и недостатки
- Преимущества: Простота монтажа и расчетов; сила тока строго контролируется и одинакова во всех точках. Активно используется в схемах делителей напряжения и для подключения измерительных приборов (амперметров).
- Недостатки: Низкая надежность. При выходе из строя (обрыве) хотя бы одного элемента разрывается вся цепь, и ток прекращается (пример — старые елочные гирлянды). Общее сопротивление цепи \(R_{экв} = R_1 + R_2 + …\) всегда больше самого большого сопротивления в цепи.
1.2. Параллельное соединение
Параллельное соединение — это метод, при котором начальные выводы (полюсы, зажимы) всех соединяемых элементов объединяются в один общий узел, а все конечные выводы (полюсы, зажимы) — в другой общий узел. Это создает несколько параллельных путей (ветвей) для прохождения тока (рис. 1, б).
Ключевой физический закон для параллельного соединения: напряжение \(U\) одинаково на всех элементах, включенных параллельно.
\(U_{общ} = U_1 = U_2 = … = U_n\)
Общий ток цепи при этом (согласно Первому закону Кирхгофа) равен сумме токов в каждой из ветвей:
\(I_{общ} = I_1 + I_2 + … + I_n\)
Этот термин также используется для описания параллельного включения источников тока или резистивных элементов с источниками тока.
Преимущества и недостатки
- Преимущества: Высокая надежность. Выход из строя (обрыв) одного элемента не влияет на работоспособность остальных ветвей (именно так подключаются все бытовые приборы в квартире). Общее сопротивление цепи всегда меньше самого малого сопротивления в цепи.
- Недостатки: Более сложная разводка; общий ток разветвляется, что требует расчета токов в каждой отдельной ветви. Короткое замыкание в одной из ветвей приводит к короткому замыканию всего источника питания.
1.3. Смешанное соединение
Смешанное (комбинированное) соединение является наиболее распространенным на практике. Оно представляет собой сочетание участков с последовательным и участков с параллельным соединением элементов (рис. 1, в).
Расчет таких схем производится поэтапно методом «свертывания»: участки с чисто последовательным или параллельным соединением рассчитываются, заменяются одним эквивалентным элементом, после чего схема упрощается. Этот процесс повторяется до тех пор, пока вся цепь не будет сведена к одному эквивалентному сопротивлению.
2. Сравнительная таблица последовательного и параллельного соединений
| Характеристика | Последовательное соединение | Параллельное соединение |
|---|---|---|
| Ток \(I\) | Одинаков для всех элементов: \(I_{общ} = I_1 = I_2 = … = I_n\) |
Общий ток равен сумме токов в ветвях: \(I_{общ} = I_1 + I_2 + … + I_n\) |
| Напряжение \(U\) | Общее напряжение равно сумме падений напряжений: \(U_{общ} = U_1 + U_2 + … + U_n\) |
Одинаково для всех элементов: \(U_{общ} = U_1 = U_2 = … = U_n\) |
| Эквивалентное сопротивление \(R_{экв}\) | Равно сумме сопротивлений: \(R_{экв} = R_1 + R_2 + … + R_n\) |
Величина, обратная \(R_{экв}\), равна сумме обратных величин: \( \frac{1}{R_{экв}} = \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n} \) |
| Надежность (при обрыве 1 элемента) | Низкая (вся цепь отказывает) | Высокая (остальные ветви продолжают работать) |
| Основное применение | Делители напряжения, измерительные шунты, амперметры, защитные предохранители | Бытовая электросеть, освещение, источники питания, вольтметры |
3. Топология и сложность электрических цепей
Геометрическая структура схемы, которая отображает исключительно способы соединения ее элементов (кто с кем связан), называется топологией электрической цепи. Это одно из важнейших понятий в теории электрических цепей, так как именно топология определяет сложность схемы и методы ее анализа.
3.1. Простые и сложные цепи
Условно цепи, схемы замещения которых содержат малое число элементов, принято называть простыми цепями. Очевидно, что цепь питания обычной электролампы относится к простым. Схемы с большим числом элементов называют сложными цепями.
Однако к топологически простым цепям относят и схемы с большим числом элементов, если все они соединены только последовательно (такие цепи называют неразветвленными) или только параллельно. Их расчет, несмотря на количество компонентов, сводится к последовательному суммированию.
Понятие сложности электрической цепи во многом обусловливается сложностью ее описания и расчета. То есть, оно носит частично качественный характер, зависящий от знаний и умений специалиста-электротехника, а также наличия у него современных программных и вычислительных средств (например, систем схемотехнического моделирования, таких как SPICE или Simulink).
3.2. Планарные и непланарные схемы
Для специалиста важно даже умение просто и наглядно изображать схемы цепей, поскольку разное их графическое представление обусловливает и разную сложность их восприятия и последующего математического описания.
Ключевым понятием здесь является планарность схемы — то есть, возможность ее изображения на плоскости (на листе) без взаимного пересечения ветвей.
Так, схему на (рис. 2, а), которая содержит пересекающиеся ветви (ветвь с резистором \(R_5\) и ветвь с источником \(E_6\)), можно перерисовать в виде, не содержащем пересекающихся ветвей (рис. 2, б). Это означает, что данная схема является планарной (плоской). Умение распознать планарность схемы и привести ее к виду без пересечений значительно упрощает ее анализ, например, при использовании метода контурных токов.
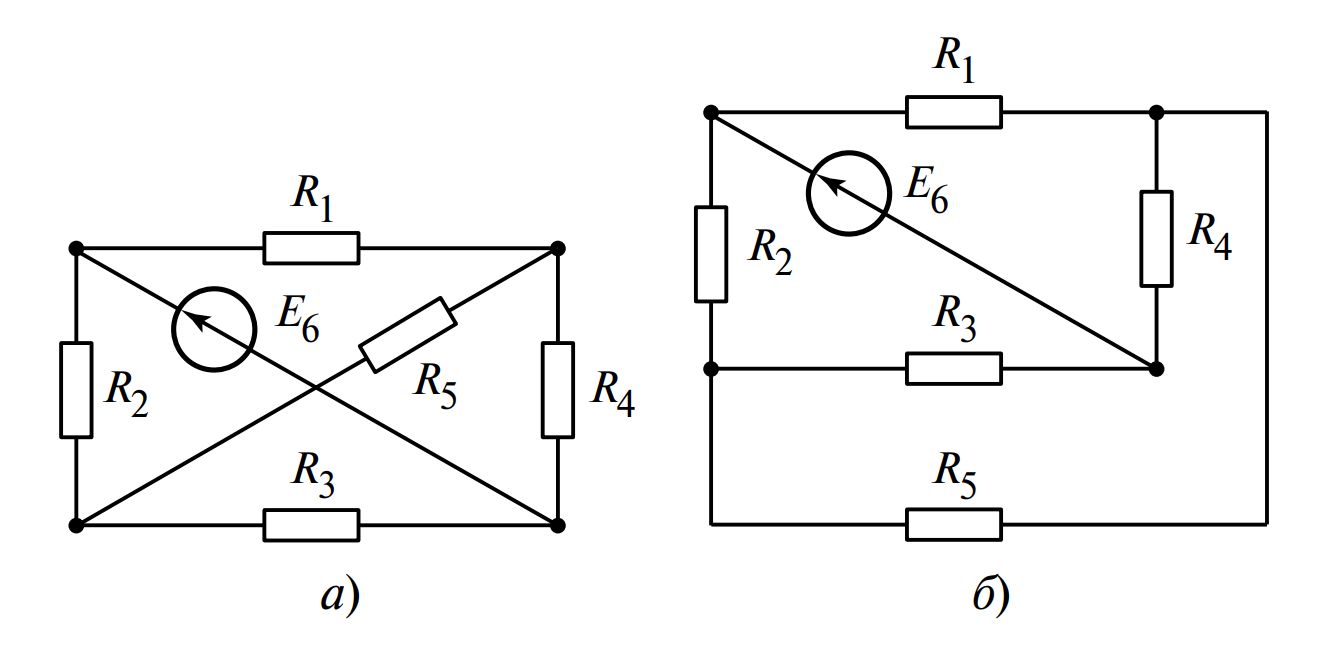
Рисунок 2. Пример планарной схемы:
а — изображенная с пересечением ветвей; б — та же схема, изображенная без пересечения ветвей
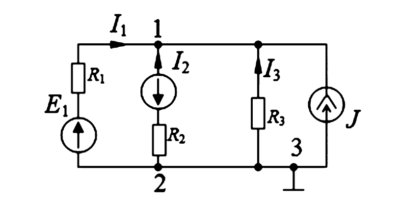
Примером непланарной схемы, то есть схемы, которую принципиально нельзя изобразить на плоскости без пересечения как минимум двух ветвей, является схема, представленная на (рис. 3). Анализ таких схем, как правило, сложнее и требует применения более универсальных методов (например, метода узловых потенциалов).
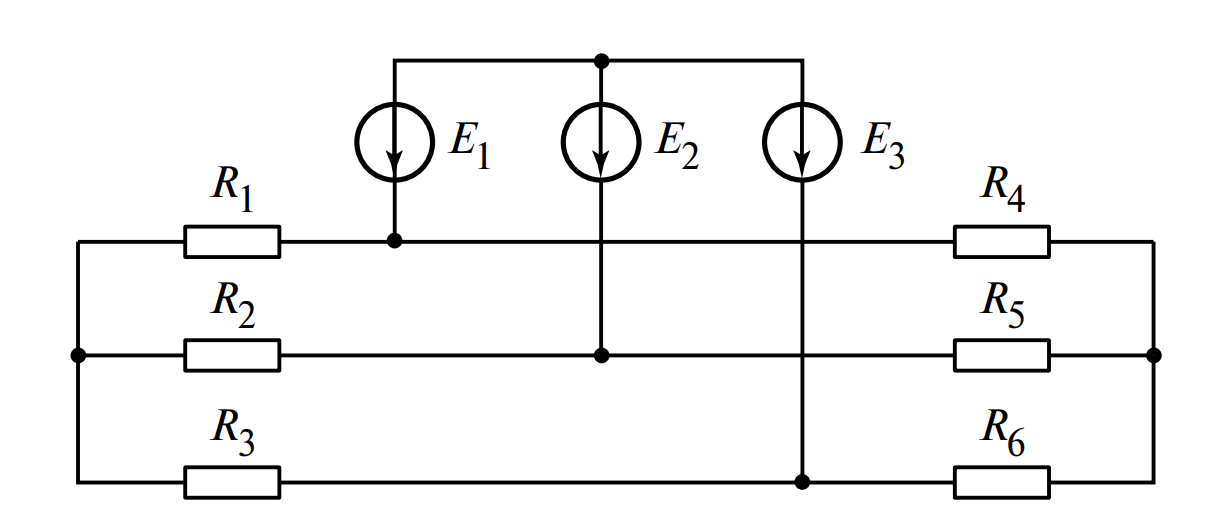
Рисунок 3. Пример непланарной (неплоской) схемы
4. Интересные факты по теме
- Законы Кирхгофа: Являются фундаментальной основой для расчета токов и напряжений в любых, сколь угодно сложных, смешанных, планарных и непланарных цепях.
- Бытовая электросеть: Все розетки и стационарные осветительные приборы в здании подключены параллельно. Это гарантирует, что на каждом из них будет одинаковое номинальное напряжение (например, 230 В) и они могут работать независимо друг от друга.
- Эволюция гирлянд: Старые новогодние гирлянды с лампами накаливания были ярким примером последовательного соединения. Перегорание (обрыв) одной лампы приводило к отказу всей гирлянды.
- Теория графов: Планарность схем — это раздел математической теории графов. Непланарная схема на (рис. 3) является классическим примером «полного графа K5» (пять узлов, соединенных друг с другом).
- Мост Уитстона: Классическая схема измерительного моста для определения сопротивления является примером смешанного, но планарного соединения.
5. Часто задаваемые вопросы (FAQ)
1. Что произойдет, если в параллельную цепь добавить еще одну ветвь?
При добавлении еще одной параллельной ветви (например, включении еще одного прибора в розетку) общее (эквивалентное) сопротивление всей цепи уменьшится. В результате, при неизменном напряжении источника, общий ток, потребляемый от источника, увеличится (в соответствии с законом Ома \(I = U / R_{экв}\)).
2. Что произойдет, если в последовательную цепь добавить еще один элемент?
При добавлении нового элемента последовательно, общее сопротивление цепи увеличится (т.к. \(R_{экв} = R_1 + R_2 + … + R_{new}\)). Как следствие, при неизменном напряжении источника, общий ток в цепи уменьшится.
3. Как рассчитать смешанную цепь?
Расчет ведется методом «свертывания» схемы. Находят простые группы (участки) с чисто последовательным или чисто параллельным соединением. Рассчитывают их эквивалентное сопротивление и «заменяют» на схеме эту группу одним эквивалентным резистором. Схема упрощается. Процесс повторяют, пока вся цепь не «свернется» к одному общему сопротивлению.
4. Почему для анализа непланарных схем не подходит метод контурных токов?
Классический метод контурных токов основан на «контурах», которые можно выделить на плоскости (как «окна» в раме). В непланарной схеме, которую нельзя «разложить» на плоскости, понятие такого «внутреннего» контура теряет однозначность. Поэтому для непланарных схем (как на рис. 3) применяют более универсальные методы, такие как метод узловых потенциалов или составление уравнений по законам Кирхгофа в общем виде.
5. Какой ГОСТ регулирует эти термины?
Основные термины и определения в области электротехники, включая «электрическая цепь» и «элемент электрической цепи», стандартизированы в ГОСТ Р 52002-2003 («Электротехника. Термины и определения основных понятий»).
Заключение
Понимание принципов последовательного, параллельного и смешанного соединений является фундаментальной основой для любого специалиста, работающего с электричеством. Эти три метода лежат в основе проектирования и анализа абсолютно всех электрических и электронных схем, от простейшей бытовой проводки до сложнейших вычислительных систем.
Освоение методов расчета, а также понимание топологических особенностей схем, включая их планарность, позволяет инженеру не только корректно анализировать поведение цепи, но и выбирать наиболее эффективные и оптимальные методы ее расчета и проектирования.
Нормативная база
Основные термины, определения и правила графического выполнения схем в Российской Федерации регламентируются стандартами Единой системы конструкторской документации (ЕСКД) и другими национальными стандартами:
- ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий. (Устанавливает термины «электрическая цепь», «элемент электрической цепи» и т.д.).
- ГОСТ 2.701-2008 — Единая система конструкторской документации (ЕСКД). Схемы. Виды и типы. Общие требования к выполнению. (Регламентирует правила изображения схем, их структуру и состав).
- ГОСТ 2.702-2008 — Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем. (Устанавливает конкретные правила построения электрических схем).
Рекомендуемая литература
- Бессонов Л. А. «Теоретические основы электротехники: Электрические цепи». — 11-е изд. — М.: Гардарики, 2007. — 701 с.
- Зевеке Г. В., Ионкин П. А., Нетушил А. В. «Основы теории цепей». — 5-е изд. — М.: Энергоатомиздат, 1989. — 528 с.
- Касаткин А. С., Немцов М. В. «Электротехника: Учебник для вузов». — 9-е изд. — М.: Академия, 2012. — 544 с.
- Нейман Л. Р., Демирчян К. С. «Теоретические основы электротехники». В 2-х томах. — 3-е изд. — Л.: Энергоиздат, 1981.
Под переходными процессами в электротехнике понимают физические явления, возникающие в электрической цепи при переходе от одного установившегося (стационарного) режима работы Читать далее...
Резонанс токов — это особое явление в электрической цепи с параллельным соединением индуктивности и емкости, при котором реактивная Читать далее...
Схема замещения электрической цепи — это ее упрощенная графическая модель, которая используется для теоретического анализа и математического расчета Читать далее...
При анализе разветвленных электрических цепей, содержащих множество узлов и ветвей, прямое использование первого и второго законов Кирхгофа Читать далее...