Несинусоидальные периодические величины: виды, ряд Фурье

Содержание страницы

Виды несинусоидальных колебаний
Теорема Фурье и гармонический анализ
Спектр несинусоидальной величины
Значение и применение гармонического анализа
Сравнительная характеристика гармонического состава сигналов
Интересные факты о гармониках и рядах Фурье
Часто задаваемые вопросы (FAQ)
Заключение

Периодическая несинусоидальная величина — это сложное периодическое колебание (например, ток или напряжение в электрической цепи), форма которого отличается от идеальной гармонической синусоиды, но которое в точности повторяется через строго определенный временной интервал, называемый периодом (\(T\)).

Исторически, фундаментальный вклад в изучение и анализ таких сложных сигналов внес французский математик и физик Жан-Батист Жозеф Фурье в начале XIX века. В 1822 году он опубликовал свою работу «Аналитическая теория тепла», где представил революционную идею: любую периодическую функцию, какой бы сложной ни была ее форма, можно представить в виде суммы простых синусоидальных колебаний (гармоник) с различными амплитудами, фазами и частотами, кратными основной.

Этот метод, известный сегодня как гармонический анализ или разложение в ряд Фурье, стал краеугольным камнем в электротехнике, радиотехнике, акустике, обработке сигналов и многих других областях науки и техники.

Виды несинусоидальных колебаний

На практике в электротехнических устройствах (преобразователях, выпрямителях, генераторах) часто встречаются несинусоидальные сигналы. На Рисунке 1 представлены графические примеры (формы) нескольких распространенных видов таких колебаний (пункты а-е).

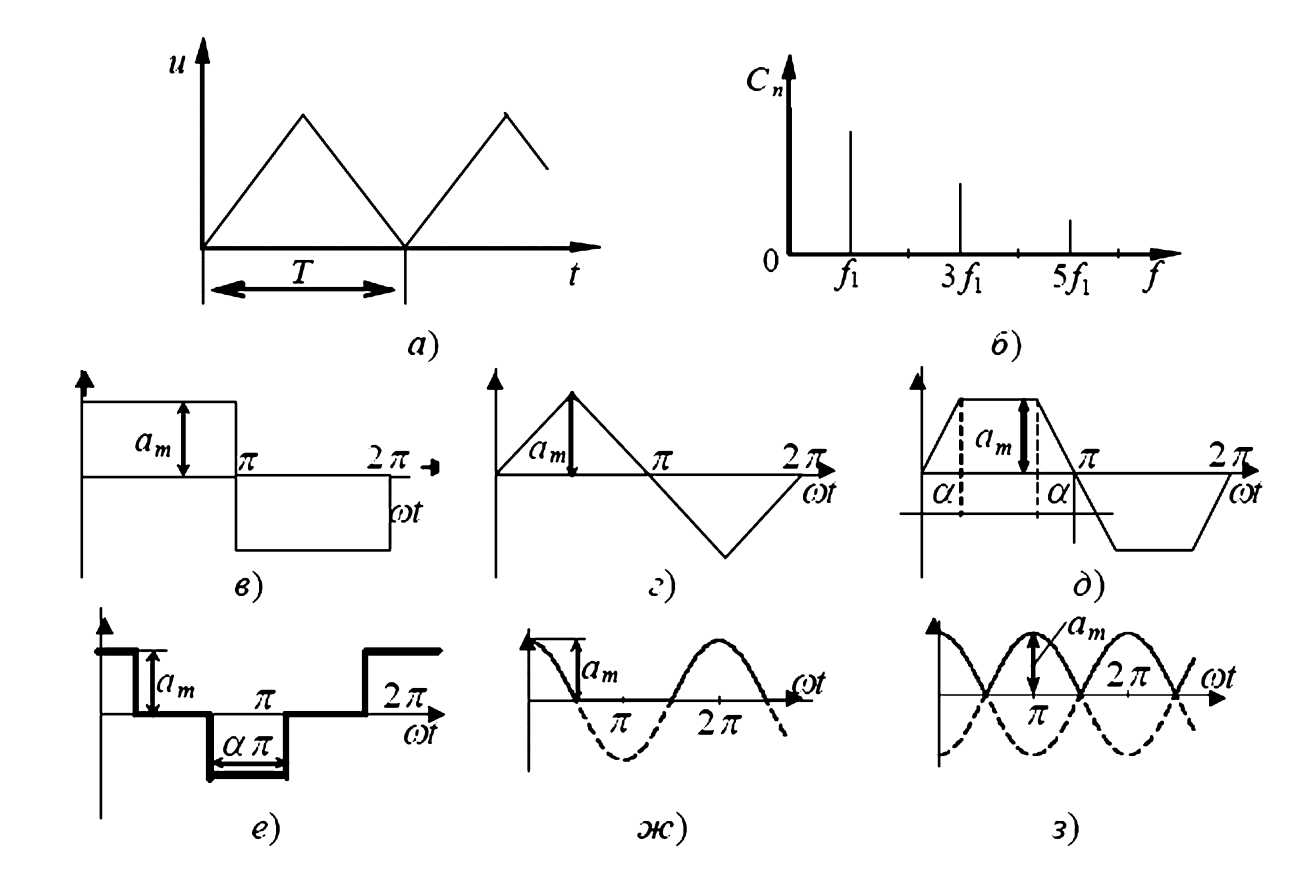
Рисунок 1 — Виды периодических несинусоидальных колебаний:
а — треугольное;
б — спектр амплитуд;
в — прямоугольное;
г — треугольное знакопеременное;
д — трапецеидальное;
е — ступенчатое;
ж — однополупериодное (выпрямленное);
з — двухполупериодное (выпрямленное).

Теорема Фурье и гармонический анализ

Можно доказать, что сумма простых синусоидальных (гармонических) величин с частотами, кратными основной, является периодической, но уже несинусоидальной (негармонической) функцией:

\[ f(t) = \sum A_n \sin(n\omega t + \alpha_n) \]

Справедливо и обратное, фундаментальное утверждение, известное как теорема Фурье. Согласно этой теореме, любая периодическая несинусоидальная функция \(f(t)\), удовлетворяющая определенным математическим условиям (условия Дирихле), может быть однозначно разложена в тригонометрический ряд (ряд Фурье). Этот ряд представляет собой сумму постоянной составляющей и бесконечного числа гармонических составляющих, частоты которых (\(n\omega\)) кратны основной (фундаментальной) частоте \(\omega\).

Разложение в ряд Фурье может быть представлено в двух эквивалентных формах:

\[ f(t) = a_0 + \sum_{n=1}^{\infty} (a_n \cos(n\omega t) + b_n \sin(n\omega t)) \quad (1) \]

Или в более компактной форме:

\[ f(t) = a_0 + \sum_{n=1}^{\infty} C_n \sin(n\omega t + \phi_n) \]

Здесь \(a_0\) — постоянная составляющая (среднее значение функции за период). Коэффициенты ряда \(a_n\), \(b_n\), амплитуда \(C_n\) и начальный фазовый угол \(\phi_n\) для \(n\)-й гармоники определяются следующими интегралами:

Постоянная составляющая (среднее значение):

\[ a_0 = \frac{1}{T} \int_{-T/2}^{T/2} f(t) dt \]

Коэффициент при косинусе \(n\)-й гармоники:

\[ a_n = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos(n\omega t) dt \]

Коэффициент при синусе \(n\)-й гармоники:

\[ b_n = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \sin(n\omega t) dt \]

Амплитуда \(n\)-й гармоники:

\[ C_n = \sqrt{a_n^2 + b_n^2} \]

Начальная фаза \(n\)-й гармоники:

\[ \text{tg}(\phi_n) = \frac{a_n}{b_n} \]

Примечание:

Компонент \(a_0\) (или \(C_0\)) представляет собой постоянную составляющую сигнала. Это то значение, которое показал бы вольтметр постоянного тока.
Составляющая с частотой \(\omega\) (при \(n=1\)) называется первой (основной) гармоникой. Ее частота совпадает с частотой самого несинусоидального сигнала.
Составляющие с частотами \(2\omega\), \(3\omega\), …, \(n\omega\) — это высшие гармоники (вторая, третья и т.д.). Именно их наличие и «искажает» исходную синусоиду.

Примеры разложения

Для наглядности в Таблице 1 приведены примеры разложения в ряд Фурье для некоторых часто встречающихся на практике несинусоидальных функций, графики которых схематично показаны на Рисунке 1.

Таблица 1. Примеры разложения несинусоидальных функций в ряд Фурье

Номер (по Рис. 1)	Наименование формы сигнала	Разложение в ряд Фурье \(f(t)\)
1в	Прямоугольное (симметричное, меандр)	\( f(t) = \frac{4a_m}{\pi} \left( \sin(\omega t) + \frac{1}{3}\sin(3\omega t) + \frac{1}{5}\sin(5\omega t) + \frac{1}{7}\sin(7\omega t) + \dots \right) \)
1г	Треугольное (знакопеременное)	\( f(t) = \frac{8a_m}{\pi^2} \left( \sin(\omega t) — \frac{1}{9}\sin(3\omega t) + \frac{1}{25}\sin(5\omega t) — \frac{1}{49}\sin(7\omega t) + \dots \right) \)
1д	Трапецеидальное	\( f(t) = \frac{4a_m}{\pi\alpha} \left( \sin(\alpha)\sin(\omega t) + \frac{\sin(3\alpha)}{9}\sin(3\omega t) + \frac{\sin(5\alpha)}{25}\sin(5\omega t) + \dots \right) \)
1е	Ступенчатое	\( f(t) = \frac{4a_m}{\pi} \left( \sin(\frac{\alpha\pi}{2})\cos(\omega t) + \frac{1}{3}\sin(\frac{3\alpha\pi}{2})\cos(3\omega t) + \frac{1}{5}\sin(\frac{5\alpha\pi}{2})\cos(5\omega t) + \dots \right) \)
1ж	Однополупериодное (выпрямленное)	\( f(t) = \frac{a_m}{\pi} + \frac{a_m}{2}\cos(\omega t) + \frac{2a_m}{\pi} \left( \frac{1}{1 \cdot 3}\cos(2\omega t) — \frac{1}{3 \cdot 5}\cos(4\omega t) + \frac{1}{5 \cdot 7}\cos(6\omega t) — \dots \right) \)
1з	Двухполупериодное (выпрямленное)	\( f(t) = \frac{2a_m}{\pi} + \frac{4a_m}{\pi} \left( \frac{1}{1 \cdot 3}\cos(2\omega t) — \frac{1}{3 \cdot 5}\cos(4\omega t) + \frac{1}{5 \cdot 7}\cos(6\omega t) — \dots \right) \)

Спектр несинусоидальной величины

Совокупность всех амплитуд \(C_n\) и соответствующих им начальных фаз \(\phi_n\) гармонических составляющих (включая постоянную составляющую \(a_0 = C_0\)) называется дискретным спектром несинусоидальной функции.

Этот спектр можно представить графически. Различают два вида спектральных диаграмм:

Амплитудный спектр: График зависимости амплитуд гармоник \(C_n\) от их частоты \(n\omega\).
Фазовый спектр: График зависимости начальных фаз \(\phi_n\) от частоты \(n\omega\).

Например, для функции, показанной на Рисунке 1а (треугольное колебание), ее амплитудный спектр будет иметь вид, показанный на Рисунке 1б. Он состоит из набора отдельных (дискретных) вертикальных линий, высота каждой из которых пропорциональна амплитуде \(C_n\) соответствующей гармоники. Из-за этого такой спектр также называют линейчатым.

Значение и применение гармонического анализа

Метод разложения несинусоидальных величин на гармонические составляющие (гармонический анализ) является фундаментальным инструментом в электротехнике, радиотехнике и теории цепей. Его применение дает ряд существенных преимуществ, но имеет и свои особенности.

Преимущества

Упрощение расчетов: Расчет линейных электрических цепей для сложных несинусоидальных сигналов сводится к набору более простых расчетов для каждой отдельной синусоидальной гармоники (используя метод комплексных амплитуд).
Принцип суперпозиции (наложения): Для линейных цепей итоговая реакция (ток или напряжение) на несинусоидальное воздействие равна сумме реакций на каждую из его гармонических составляющих.
Анализ качества энергии: Позволяет оценить «искаженность» формы напряжения в электросетях. Выделение амплитуд нежелательных высших гармоник (особенно 3-й, 5-й, 7-й) критически важно, так как они могут вызывать перегрев оборудования, сбои в работе автоматики и снижение КПД.
Проектирование фильтров: Дает возможность рассчитать и спроектировать электрические фильтры для подавления (ослабления) определенных вредных гармоник или, наоборот, для выделения нужных (например, в радиоприемниках).

Ограничения и недостатки

Применимость к линейным цепям: Принцип суперпозиции, лежащий в основе метода, строго выполняется только для линейных цепей (где параметры R, L, C постоянны и не зависят от тока или напряжения).
Бесконечный ряд: Теоретически, ряд Фурье является бесконечным. На практике для инженерных расчетов его «обрывают», ограничиваясь конечным числом гармоник (обычно 3-10), что вносит определенную погрешность в расчеты.
Только для периодических функций: Классический ряд Фурье применим только к строго периодическим процессам. Для анализа непериодических (одиночных) сигналов, таких как импульсы, используется его обобщение — интеграл Фурье (преобразование Фурье).

Сравнительная характеристика гармонического состава сигналов

Различные формы несинусоидальных сигналов отличаются содержанием высших гармоник, что определяет их спектральный состав и влияние на электрические цепи.

Таблица 2. Сравнение спектрального состава различных сигналов

Характеристика	Прямоугольный (меандр, Рис. 1в)	Треугольный (Рис. 1г)	Двухполупериодный (Рис. 1з)
Постоянная составляющая (\(a_0\))	Отсутствует (для симметричного)	Отсутствует (для симметричного)	Присутствует (\(\frac{2a_m}{\pi}\))
Наличие первой гармоники (\(n=1\))	Да (амплитуда \(\frac{4a_m}{\pi}\))	Да (амплитуда \(\frac{8a_m}{\pi^2}\))	Отсутствует
Наличие четных гармоник (\(n=2, 4, 6, \dots\))	Только нечетные	Только нечетные	Только четные (и \(a_0\))
Скорость убывания амплитуд гармоник	Медленная (пропорционально \(\frac{1}{n}\))	Быстрая (пропорционально \(\frac{1}{n^2}\))	Быстрая (пропорционально \(\frac{1}{n^2}\))
Оценка «искаженности»	Очень высокая. Спектр насыщен высшими гармониками.	Низкая. Форма сигнала «гладкая», быстро приближается к синусоиде.	Высокая, но основная частота пульсаций (\(2\omega\)) вдвое выше сетевой.

Интересные факты о гармониках и рядах Фурье

Синтез звука: Первые электронные музыкальные синтезаторы (например, орган Хаммонда) работали по принципу, обратному анализу Фурье: они «собирали» (синтезировали) сложные тембры звука, суммируя простые синусоиды с разными амплитудами.
Сжатие изображений (JPEG): Алгоритм сжатия JPEG использует разновидность преобразования Фурье (дискретное косинусное преобразование, ДКП). Он раскладывает изображение на «пространственные гармоники», а затем отбрасывает «незначительные» (высокочастотные), что и обеспечивает сжатие.
Феномен Гиббса: При попытке восстановить сигнал с резкими разрывами (как у прямоугольного импульса) из его ряда Фурье, даже при суммировании очень большого числа гармоник, на краях разрыва всегда остаются небольшие «выбросы» (около 9%). Это фундаментальное свойство называется явлением Гиббса.
Музыка 8-бит: Звуковые чипы старых игровых приставок (NES, Game Boy) не могли генерировать чистые синусоиды. Они создавали музыку, используя в основном прямоугольные (меандр) и треугольные волны, что и придает «chiptune» музыке ее характерное звучание, богатое гармониками.
Диагностика двигателей: Анализируя спектр вибраций работающего двигателя (вибродиагностика), инженеры могут по амплитудам определенных гармоник точно определить дефекты: дисбаланс ротора, повреждение подшипника или несоосность валов.
Анализ ЭКГ: В медицине гармонический анализ электрокардиограммы (ЭКГ) помогает выявлять скрытые патологии сердца, которые не видны при простом визуальном осмотре графика.
Только нечетные гармоники: Любой несинусоидальный сигнал, обладающий «симметрией полуволны» (когда вторая половина периода в точности повторяет первую, но с обратным знаком, как у меандра или треугольной волны), в своем составе будет содержать только нечетные гармоники (1-ю, 3-ю, 5-ю и т.д.).

Часто задаваемые вопросы (FAQ)

1. Что такое несинусоидальная величина простыми словами?

Это любой повторяющийся (периодический) сигнал, график которого не является плавной синусоидой. Например, «зубья» пилы, прямоугольные импульсы в компьютере или искаженное напряжение в розетке из-за мощной нагрузки.

2. Зачем вообще раскладывать сигнал в ряд Фурье?

Это главный способ упростить сложную задачу. Рассчитывать, как сложный несинусоидальный сигнал пройдет через электрическую цепь (например, фильтр), невероятно сложно. Гораздо проще рассчитать, как через нее пройдет каждая из его простых синусоидальных «составляющих» (гармоник) по отдельности, а потом просто сложить результаты (принцип суперпозиции).

3. Что такое основная гармоника и высшие гармоники?

Основная (первая) гармоника — это синусоида, частота которой равна частоте самого несинусоидального сигнала (например, 50 Гц для электросети). Высшие гармоники — это «примеси» в виде синусоид с частотами, кратными основной (100 Гц — 2-я, 150 Гц — 3-я, 250 Гц — 5-я и т.д.). Они искажают форму основного сигнала.

4. Всегда ли в несинусоидальном сигнале есть первая (основная) гармоника?

Нет. Яркий пример — сигнал после двухполупериодного выпрямителя (см. Рис. 1з и Таблицу 1). Если на входе было 50 Гц, то на выходе постоянная составляющая \(a_0\) и гармоники с частотами 100 Гц, 200 Гц, 300 Гц и т.д. А «родная» частота 50 Гц (первая гармоника) в спектре отсутствует.

5. Что такое коэффициент гармонических искажений (THD)?

Это стандартная мера «загрязненности» синусоидального сигнала высшими гармониками. Он вычисляется как отношение суммарной мощности (или среднеквадратичного значения) всех высших гармоник к мощности (или среднеквадратичному значению) первой (основной) гармоники. Чем ниже THD, тем «чище» синусоида.

6. Почему в симметричных прямоугольных импульсах (меандре) нет четных гармоник?

Это связано с математическим свойством «симметрии полуволны» (\(f(t) = -f(t + T/2)\)). Из-за этой симметрии при вычислении интегралов для коэффициентов \(a_n\) и \(b_n\) (формулы (1)) все составляющие для четных \(n\) (n=2, 4, 6…) взаимно уничтожаются и обращаются в ноль.

7. В чем разница между рядом Фурье и преобразованием Фурье?

Ряд Фурье (то, что описано в статье) применяется только для периодических сигналов (которые бесконечно повторяются). Он дает дискретный (линейчатый) спектр — набор отдельных частот. Преобразование Фурье (интеграл Фурье) — это более общий инструмент для непериодических сигналов (например, одиночный импульс, затухающее колебание). Он дает непрерывный (сплошной) спектр.

Заключение

Понимание природы несинусоидальных периодических величин является критически важным аспектом в современной электротехнике и радиотехнике. Теорема Фурье предоставляет мощный математический аппарат для их анализа, позволяя «разложить» любой сложный периодический процесс на сумму простых гармонических колебаний.

Такой подход (гармонический анализ) позволяет применять к сложным сигналам хорошо разработанные методы расчета линейных цепей для синусоидального тока, оценивать качество электрической энергии (уровень гармонических искажений) и целенаправленно проектировать фильтрующие устройства. Спектральное представление сигнала дает наглядную картину его частотного состава, что незаменимо при решении задач обработки сигналов, связи и акустики.

Нормативные документы

ГОСТ 32144-2013 — Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. (Данный межгосударственный стандарт устанавливает предельно допустимые значения для коэффициентов гармонических составляющих напряжения в электрических сетях).

Список литературы

Бессонов Л.А. Теоретические основы электротехники (ТОЭ). Электрические цепи. — 11-е изд. — М.: Гадарика, 2007. — 701 с.
Зевеке Г.В., Ионкин П.А., Нетушил А.В. Основы теории цепей. — М.: Энергоатомиздат, 1989. — 528 с.
Сергиенко А. Б. Цифровая обработка сигналов: Учебник для вузов. — 3-е изд. — СПб.: Питер, 2011. — 751 с.
Оппенгейм А. В., Шафер Р. В. Цифровая обработка сигналов. — 2-е изд. — М.: Техносфера, 2009. — 856 с.