Мощность и КПД источников электрической энергии

Содержание страницы

1. Мощность и КПД источников ЭДС
2. Мощность и КПД источников тока
3. Преимущества и недостатки использования моделей
4. Сравнение моделей источников ЭДС и тока
5. Интересные факты по теме
6. Часто задаваемые вопросы (FAQ)
Заключение

Мощность и коэффициент полезного действия (КПД) являются ключевыми характеристиками любого источника электрической энергии, будь то гальванический элемент, аккумулятор или электромеханический генератор. Эти параметры определяют, какое количество энергии источник способен отдать в полезную нагрузку и какая доля энергии теряется внутри самого источника. Концепции ЭДС, внутреннего сопротивления и потерь мощности были сформулированы в XIX веке благодаря работам Георга Ома, Джеймса Джоуля и Эмиля Ленца, что заложило теоретическую основу для анализа и проектирования всех электрических цепей.

1. Мощность и КПД источников ЭДС

Рассмотрим электрическую цепь, представленную на рисунке 1. В этой схеме источник, обладающий электродвижущей силой (ЭДС) $E$ и внутренним сопротивлением $R_г$, подключен к внешней нагрузке с сопротивлением $R_н$. В результате в замкнутой цепи начинает протекать электрический ток $I$.

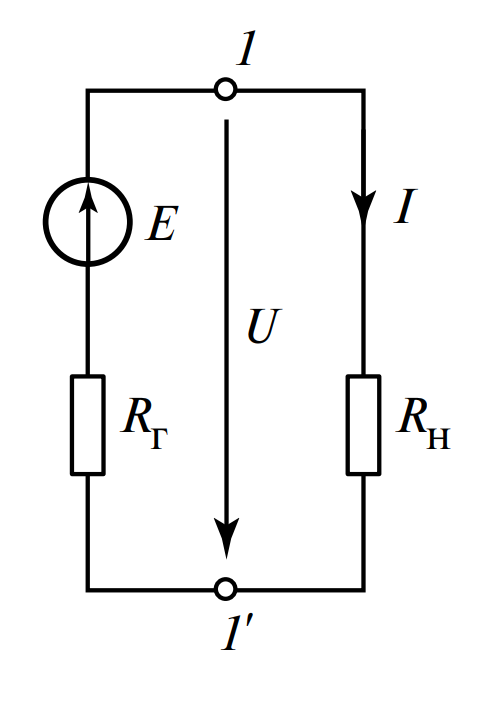
Рисунок 1 — Схема подключения источника ЭДС с внутренним сопротивлением $R_г$ к нагрузке $R_н$

Работа $A$, совершаемая сторонними силами внутри источника (с напряженностью $E_{ст}$) по перемещению заряда $Q$, определяется как:

$$A = \int_1^2 E_{ст} dl = QU \quad (1)$$

При постоянном токе $I = Q/t$, работа за время $t$ равна:

$$A = UIt \quad (2)$$

Тогда мощность источника $P$, то есть скорость совершения им работы, определяется как:

$$P = UI \quad (3)$$

Напряжение $U$ на зажимах источника (которое равно напряжению на нагрузке $R_н$) связано с ЭДС $E$ и внутренним падением напряжения согласно закону Ома для полной цепи: $U = E — IR_г$. Подставляя это в формулу (3), получаем мощность, отдаваемую источником во внешнюю цепь (полезную мощность):

$$P_{ист} = (E — R_гI)I = EI — R_гI^2 \quad (4)$$

Баланс мощностей

В любой электрической цепи должен соблюдаться баланс мощностей. Это фундаментальный принцип, утверждающий, что суммарная мощность, генерируемая всеми источниками, равна суммарной мощности, потребляемой всеми нагрузками (приемниками) в цепи.

$$P_{ист} = P_н \quad (5)$$

Мощность, потребляемая нагрузкой $R_н$, рассеивается в виде тепла. Согласно закону Джоуля—Ленца, эта мощность потребления равна $P_н = R_нI^2$. Приравнивая это к выражению (4) в соответствии с балансом (5), получаем уравнение баланса мощностей для данной цепи:

$$EI — R_гI^2 = R_нI^2 \quad (6)$$

Из этого уравнения баланса можно выразить ток $I$, протекающий в цепи, показанной на рисунке 1. Это выражение является законом Ома для замкнутой цепи:

$$I = \frac{E}{R_н + R_г} \quad (7)$$

Реальные и идеальные источники ЭДС

Анализ формул (4) и (7) показывает, что мощность, отдаваемая источником в нагрузку, зависит как от сопротивления нагрузки $R_н$, так и от внутреннего сопротивления самого источника $R_г$. Источник с $R_г > 0$ называют реальным источником ЭДС. Его мощность всегда будет меньше мощности идеального источника ЭДС, у которого по определению $R_г = 0$. Идеальный источник развивал бы полную мощность $P’_{ист} = EI$.

Примечание: Схематически реальный источник ЭДС можно представить как последовательное соединение идеального источника $E$ и резистивного элемента $R_г$, как показано на рисунке 2 (а). Идеальный источник показан на рисунке 2 (б). Эта модель также известна как эквивалентный генератор Тевенина.

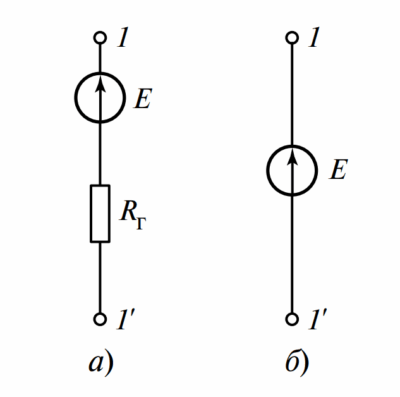
Рисунок 2 — Схемы замещения генератора: а) реальный источник ЭДС с внутренним сопротивлением; б) идеальный источник ЭДС

Коэффициент полезного действия (КПД)

Для количественной оценки эффективности передачи энергии от источника к нагрузке вводится коэффициент полезного действия (КПД), обозначаемый греческой буквой $\eta$ (эта).

КПД источника определяется как отношение полезной мощности, отдаваемой в нагрузку ( $P_{ист}$ или $P_н$ ), к полной мощности, развиваемой ЭДС ( $P’_{ист} = EI$):

$$\eta = \frac{P_{ист}}{P’_{ист}} = \frac{UI}{EI} = \frac{U}{E} \quad (8)$$

Используя ранее полученные выражения (4) и (7), можно выразить КПД через сопротивления цепи. Компонент $EI$ в формуле (4) — это полная мощность, а $R_гI^2$ — мощность потерь внутри источника.

$$\eta = \frac{EI — R_гI^2}{EI} = 1 — \frac{R_гI}{E}$$

Подставив сюда выражение для тока $I$ из (7), получаем окончательную формулу:

$$\eta = 1 — \frac{R_г \left( \frac{E}{R_н + R_г} \right)}{E} = 1 — \frac{R_г}{R_н + R_г} \quad (9)$$

На практике КПД часто выражают в процентах, для этого достаточно умножить полученное безразмерное значение на 100%:

$$\eta (\%) = \eta \cdot 100\% = \left(1 — \frac{R_г}{R_н + R_г}\right) \cdot 100\% \quad (10)$$

Пример 1. Рассчитаем КПД источника ЭДС (схема на рисунке 1) со следующими параметрами: $E = 10 \text{ В}$, $R_г = 1 \text{ Ом}$. Источник подключен к нагрузке с сопротивлением $R_н = 9 \text{ Ом}$.

Согласно выражению (9):

$$\eta = 1 — \frac{1}{9 + 1} = 1 — \frac{1}{10} = 1 — 0.1 = 0.9$$

Таким образом, КПД источника составляет 0.9, или 90%.

Из анализа формул (8)-(10) очевидно, что максимальный КПД, равный 1 (или 100%), достигается только в гипотетическом случае идеального источника ($R_г = 0$). Для любого реального источника КПД всегда будет меньше 1. При фиксированном сопротивлении нагрузки $R_н$, КПД источника тем выше, чем меньше его внутреннее сопротивление $R_г$. По этой причине при проектировании и создании источников ЭДС (например, генераторов или гальванических элементов) инженеры всегда стремятся конструктивно уменьшить их внутреннее сопротивление для минимизации потерь.

2. Мощность и КПД источников тока

Аналогичный анализ можно провести для источника тока. Эта модель менее интуитивна, но широко используется в теории цепей и особенно в электронике (например, при анализе транзисторных каскадов). Рассмотрим схему на рисунке 3, где реальный источник тока, характеризуемый током $J$ и внутренней проводимостью $G_г$, подключен к нагрузке с проводимостью $G_н$.

(Примечание: проводимость $G$ — величина, обратная сопротивлению, $G = 1/R$).

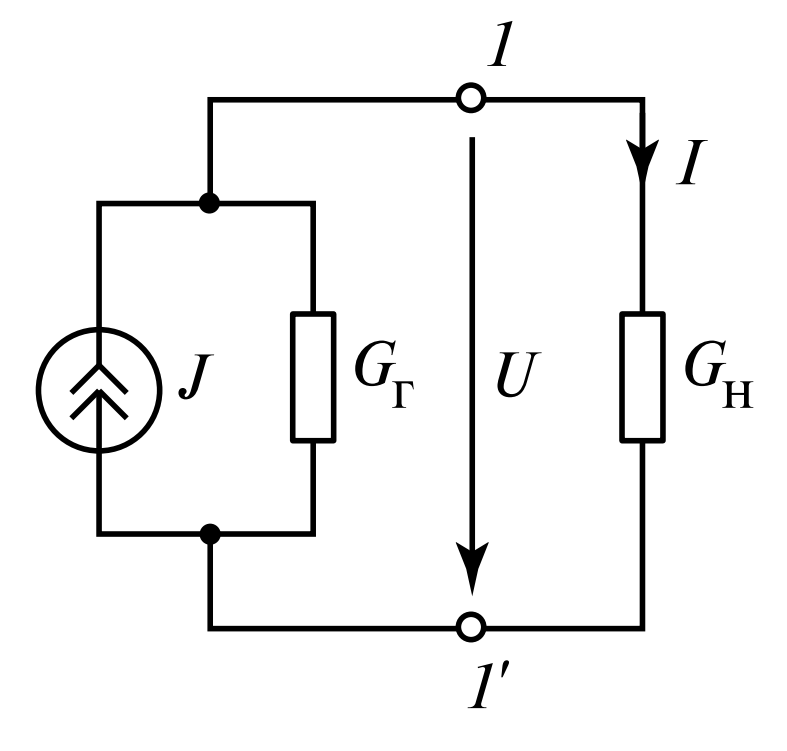
Рисунок 3 — Схема подключения источника тока с внутренней проводимостью $G_г$ к нагрузке $G_н$

Ток $J$ источника разветвляется: часть тока $I$ идет в нагрузку, а часть тока $I_г$ ответвляется во внутреннюю проводимость $G_г$. Ток $I$, отдаваемый источником во внешнюю цепь, равен $I = J — I_г = J — G_гU$, где $U$ — напряжение на зажимах источника. Тогда мощность, отдаваемая источником в нагрузку:

$$P_{ист} = UI = U(J — G_гU) = JU — G_гU^2 \quad (11)$$

Эта мощность (11) очевидно меньше мощности идеального источника тока. Идеальный источник тока — это модель с нулевой внутренней проводимостью ($G_г = 0$), или, что то же самое, с бесконечным внутренним сопротивлением. Мощность идеального источника была бы равна $P’_{ист} = JU$.

Примечание: Схемы замещения реального и идеального источников тока показаны на рисунке 4. Модель реального источника тока также известна как эквивалентный генератор Нортона. Модели Тевенина (рис. 2а) и Нортона (рис. 4а) являются взаимно эквивалентными.

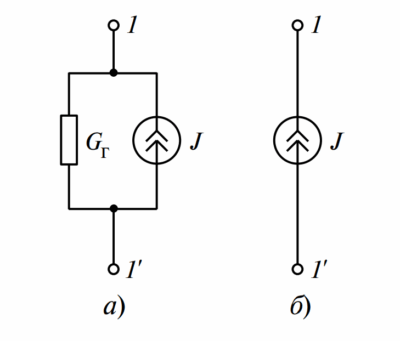
Рисунок 4 — Схемы замещения генератора: а) реальный источник тока с внутренней проводимостью; б) идеальный источник тока

Коэффициент полезного действия (КПД) для источника тока также определяется как отношение полезной мощности к полной:

$$\eta = \frac{P_{ист}}{P’_{ист}} = \frac{JU — G_гU^2}{JU} = 1 — \frac{G_гU}{J} \quad (12)$$

Поскольку $U = J / (G_н + G_г)$, подставив $U$, получаем формулу, аналогичную (9):

$$\eta = 1 — \frac{G_г}{G_н + G_г} \quad (13)$$

Вывод: КПД реального источника тока всегда меньше единицы (100%). При заданной проводимости нагрузки $G_н$, эффективность источника будет тем выше, чем меньше его внутренняя проводимость $G_г$. Поэтому при создании источников, работающих в режиме, близком к источнику тока, стремятся максимально увеличить их внутреннее сопротивление (что эквивалентно уменьшению внутренней проводимости $G_г$).

3. Преимущества и недостатки использования моделей

Обе модели — источник ЭДС (Тевенина) и источник тока (Нортона) — описывают один и тот же реальный источник, но с разных точек зрения.

Преимущества: Эти модели значительно упрощают анализ сложных электрических цепей, позволяя заменить сложную часть схемы одним эквивалентным источником. Модель Тевенина (ЭДС) удобна, когда внутреннее сопротивление источника мало. Модель Нортона (ток) удобна, когда внутреннее сопротивление велико.
Недостатки: Модели являются линейными. В реальности внутреннее сопротивление $R_г$ или проводимость $G_г$ могут быть нелинейными, то есть зависеть от протекающего тока, температуры или степени заряда (для аккумуляторов). Также КПД не является константой источника, а зависит от соотношения его $R_г$ и $R_н$ нагрузки.

4. Сравнение моделей источников ЭДС и тока

Характеристика	Источник ЭДС (Модель Тевенина)	Источник тока (Модель Нортона)
Идеальная модель	Идеальный источник напряжения (ЭДС)	Идеальный источник тока
Параметр потерь	Внутреннее сопротивление $R_г$ (Ом)	Внутренняя проводимость $G_г$ (Сименс)
Условие идеальности	$R_г \to 0$	$G_г \to 0$ (или $R_г \to \infty$)
Формула КПД	$\eta = 1 — \frac{R_г}{R_н + R_г}$	$\eta = 1 — \frac{G_г}{G_н + G_г}$
Цель оптимизации (для $\eta \to 100\%$)	Минимизировать $R_г$	Минимизировать $G_г$ (т.е. максимизировать $R_г$)

Соответствие стандартам: Все буквенные обозначения (E, J, I, R, G, U, P) и термины (ЭДС, КПД, мощность, проводимость), используемые в данном материале, соответствуют действующим межгосударственным и национальным стандартам, таким как ГОСТ Р МЭК 60027-1-2009 (Обозначения буквенные, применяемые в электротехнике) и ГОСТ Р 52002-2003 (Электротехника. Термины и определения основных понятий).

5. Интересные факты по теме

Теорема о максимальной мощности: Максимальный КПД (близкий к 100%) достигается, когда $R_н \gg R_г$. Однако, максимальная *мощность* в нагрузке ($P_н$) выделяется при условии $R_н = R_г$. В этом режиме КПД составляет ровно 50%. Это фундаментальный компромисс в электротехнике и электронике.
Независимое открытие: Закон о тепловом действии тока был открыт практически одновременно и независимо друг от друга англичанином Джеймсом Прескоттом Джоулем (1841 г.) и российским физиком Эмилием Ленцем (1842 г.), поэтому он носит двойное имя.
Реальные $R_г$: Внутреннее сопротивление сильно варьируется. У мощного автомобильного аккумулятора оно составляет сотые доли Ома (поэтому он может отдать ток в сотни ампер), а у 9-вольтовой батареи типа «Крона» — несколько Ом.
Происхождение термина ЭДС: Сам термин «электродвижущая сила» был введен Гансом Кристианом Эрстедом в 1820-х годах для описания «конфликта», создающего электричество.
Практический источник тока: Биполярный транзистор в схеме с общей базой или общим эмиттером в активном режиме работы является отличным практическим примером реального источника тока, так как его выходное сопротивление (аналог $1/G_г$) очень велико.

6. Часто задаваемые вопросы (FAQ)

1. Что такое ЭДС (E) и чем она отличается от напряжения (U)?

Ответ: ЭДС (Электродвижущая сила) — это физическая величина, характеризующая работу сторонних (неэлектрических) сил по перемещению единичного заряда внутри источника. Это «внутренняя» характеристика. Напряжение (U) — это разность потенциалов на зажимах (клеммах) источника. Напряжение равно ЭДС только в режиме холостого хода (когда ток не течет). При наличии тока $I$, напряжение всегда меньше ЭДС на величину внутреннего падения: $U = E — IR_г$.

2. Почему нельзя добиться КПД 100% в реальном источнике?

Ответ: Любой реальный материал, из которого изготовлен источник (провода обмоток генератора, электролит и электроды батареи), обладает электрическим сопротивлением. При протекании тока через это внутреннее сопротивление $R_г$ на нем неизбежно выделяется тепловая мощность $P_{потерь} = I^2R_г$ (закон Джоуля-Ленца). Эти потери и не позволяют достичь 100% эффективности.

3. Что такое режим короткого замыкания (КЗ)?

Ответ: Это аварийный режим, при котором сопротивление нагрузки $R_н = 0$ (например, при соединении клемм источника толстым проводом). Согласно формуле (7), ток в цепи достигает максимального значения: $I_{кз} = E / R_г$. При этом вся мощность источника рассеивается внутри него, а полезная мощность $P_н = I^2 R_н = 0$. КПД в режиме КЗ равен нулю.

4. Что такое режим холостого хода (ХХ)?

Ответ: Это режим, при котором к источнику не подключена нагрузка (цепь разомкнута), что эквивалентно $R_н = \infty$. Согласно формуле (7), ток в цепи $I = 0$. Внутреннее падение напряжения отсутствует ($IR_г = 0$), и напряжение на зажимах равно ЭДС: $U_{хх} = E$. Полезная мощность $P_н$ также равна нулю, так как нет тока.

5. Когда важнее максимальный КПД, а когда — максимальная мощность?

Ответ: В силовой электротехнике и энергетике (ЛЭП, электростанции, блоки питания) приоритетом является максимальный КПД для снижения потерь энергии и нагрева. В слаботочных цепях (аудио, телекоммуникации) часто важна передача максимальной мощности от одного каскада к другому (например, от усилителя к антенне). В этом случае нагрузку согласовывают ($R_н = R_г$) и мирятся с КПД 50%.

Заключение

Понимание мощности и коэффициента полезного действия (КПД) является фундаментальной задачей при анализе любой электрической цепи. Мощность, отдаваемая источником, всегда ограничивается его внутренними параметрами, которые приводят к неизбежным потерям энергии.

Источник ЭДС (модель Тевенина) и источник тока (модель Нортона) — это два эквивалентных способа описания реального источника. Ключевой вывод заключается в том, что внутреннее сопротивление $R_г$ (или внутренняя проводимость $G_г$) является параметром, определяющим внутренние потери. Оптимизация источника для повышения эффективности всегда сводится к конструктивному уменьшению $R_г$ (для источника ЭДС) или $G_г$ (для источника тока) с целью достижения максимальной эффективности передачи энергии в нагрузку.

Нормативная база

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий.
ГОСТ Р МЭК 60027-1-2009 — Обозначения буквенные, применяемые в электротехнике. Часть 1. Общие положения.
ГОСТ 2.721-74 — Единая система конструкторской документации. Обозначения условные графические в схемах. Обозначения общего применения.

Список литературы

Бессонов Л.А. Теоретические основы электротехники (ТОЭ). Электрические цепи. — 11-е изд. — М.: Гардарики, 2014.
Зевеке Г.В., Ионкин П.А., Нетушил А.В. Основы теории цепей. — 5-е изд. — М.: Энергоатомиздат, 1989.
Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов. — М.: Энергоатомиздат, 2005.