Метод смешанных величин для расчета электрических цепей

Содержание страницы

Методика расчета и пример
Преимущества и недостатки метода
Сравнение базовых методов анализа цепей
Интересные факты по теме
FAQ: Часто задаваемые вопросы
Заключение

Метод смешанных величин (МСВ), также известный как гибридный метод, — это универсальный подход к анализу сложных линейных электрических цепей. Его ключевая особенность заключается в том, что он позволяет рассчитывать схемы, которые содержат одновременно идеальные источники ЭДС (напряжения) и идеальные источники тока.

Этот метод был разработан для преодоления ограничений классических подходов:

Метод узловых напряжений (МУН), основанный исключительно на первом законе Кирхгофа, удобен для цепей с источниками тока, но создает трудности при наличии идеальных источников ЭДС (т.к. ток через такой источник не определен его напряжением).
Метод контурных токов (МКТ), основанный исключительно на втором законе Кирхгофа, эффективен для цепей с источниками ЭДС, но неприменим в чистом виде, если в схеме есть идеальные источники тока (т.к. напряжение на таком источнике не определено его током).

МСВ элегантно решает эту проблему, используя оба закона Кирхгофа одновременно. В качестве искомых «смешанных» переменных (или базисных величин) в этом методе выступает комбинированный набор узловых потенциалов (или напряжений) и контурных токов.

Методика расчета и пример

При расчете цепей методом смешанных величин используется следующая общая методика:

Разбиение цепи: Мысленно цепь разбивается на две подцепи.
- К первой подцепи (условно «токовой») относят все идеальные источники тока.
- Ко второй подцепи (условно «ЭДС») относят все идеальные источники ЭДС.
Распределение резистивных элементов: Пассивные (резистивные) элементы распределяют между этими двумя подцепями, исходя из удобства составления уравнений.
- К первой подцепи (где будут использоваться узловые потенциалы) удобнее относить элементы, заданные проводимостью (G).
- Ко второй подцепи (где будут использоваться контурные токи) удобнее относить элементы, заданные сопротивлением (R).
Выбор базисных переменных: Формируется набор смешанных величин: узловые потенциалы для первой подцепи и контурные токи для второй.
Составление системы: На основе законов Кирхгофа составляется система гибридных (смешанных) уравнений относительно выбранных переменных.
Решение: Решается полученная система линейных алгебраических уравнений, находятся базисные переменные.
Постобработка: Используя найденные базисные переменные, по закону Ома и законам Кирхгофа определяются все остальные искомые токи и напряжения в цепи.

Пример 1. Расчет простой смешанной цепи

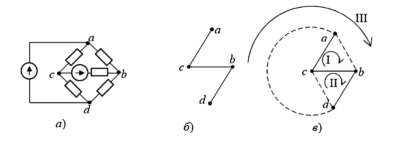
Рассмотрим применение метода для составления и решения смешанных уравнений для цепи, изображенной на Рис. 1, а). Эта схема содержит как источник тока $J_1$, так и источник ЭДС $E_2$, что делает ее идеальным кандидатом для МСВ.

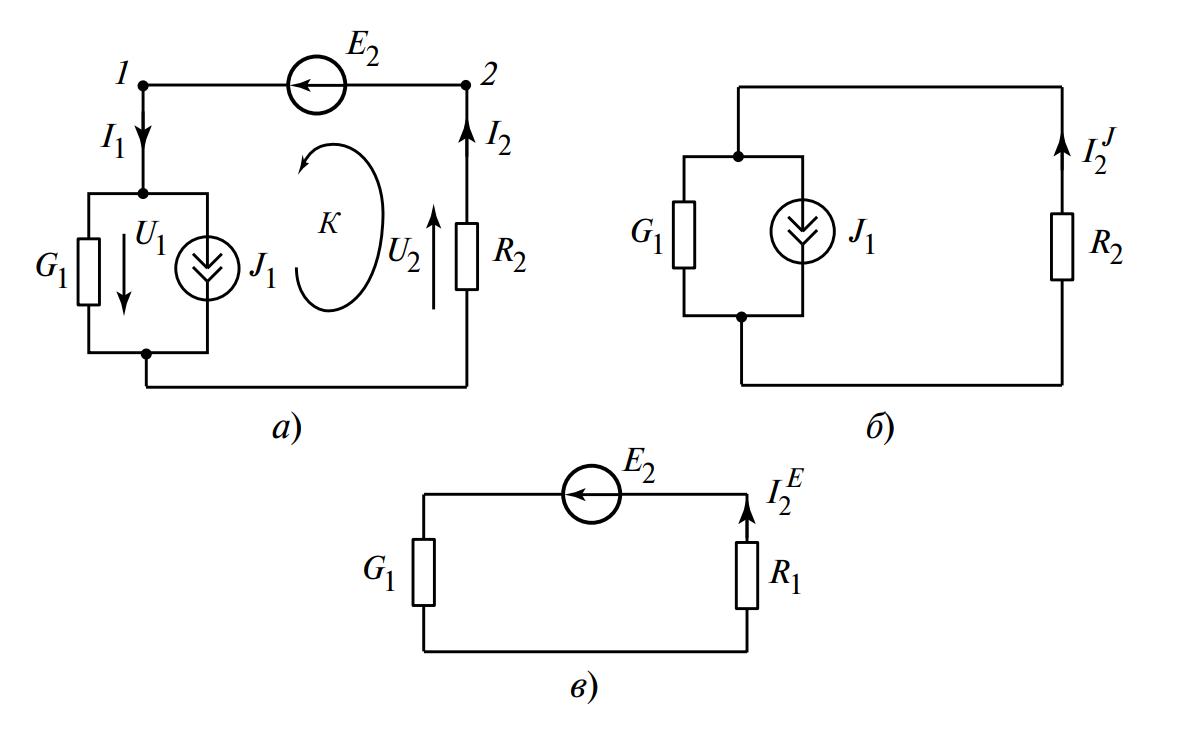
Схемы для расчета цепи методом смешанных величин

Рис. 1. Схемы расчета цепи с источниками ЭДС и тока: а) — исходная цепь с двумя источниками; б) — выделенная подцепь с источником тока; в) — выделенная подцепь с источником ЭДС.

Для анализа этой цепи вначале запишем уравнения на основе обоих законов Кирхгофа. Для узла 1 (верхнего) по первому закону Кирхгофа (сумма токов равна нулю):

$$I_1 — I_2 = 0$$

Для контура, включающего оба элемента и источник ЭДС, по второму закону Кирхгофа (сумма напряжений равна ЭДС):

$$U_1 + U_2 = E_2$$

Теперь подставим в эти уравнения компонентные уравнения для элементов. Элемент 1 (слева) — это источник тока $J_1$ с параллельной проводимостью $G_1$, его ток $I_1$ описывается как:

$$I_1 = G_1 U_1 + J_1$$

Элемент 2 (справа) — это резистивный элемент $R_2$, напряжение на нем $U_2$ описывается по закону Ома:

$$U_2 = R_2 I_2$$

Теперь выберем смешанные величины. В качестве потенциальной переменной выберем потенциал узла 1, $\phi_1$. Принимая потенциал нижнего узла за ноль, получаем $U_1 = \phi_1$. В качестве токовой переменной выберем контурный ток $I_K$, который в данной простой схеме равен току $I_2$, то есть $I_K = I_2$.

Подставим эти переменные и компонентные уравнения в исходные законы Кирхгофа:

Из $I_1 — I_2 = 0$ получаем $(G_1 U_1 + J_1) — I_2 = 0$. Заменяя переменные: $G_1 \phi_1 + J_1 — I_K = 0$, или $G_1 \phi_1 — I_K = -J_1$.
Из $U_1 + U_2 = E_2$ получаем $U_1 + (R_2 I_2) = E_2$. Заменяя переменные: $\phi_1 + R_2 I_K = E_2$.

В результате мы получаем систему смешанных уравнений. В общем виде ее можно записать так:

$$ \begin{cases} G_{11}\phi_1 — I_K = J_{11} \\ \phi_1 + R_{11}I_K = E_{11} \end{cases} \quad (1) $$

Где для нашего конкретного примера (Рис. 1) коэффициенты равны:

$G_{11} = G_1$
$J_{11} = -J_1$
$R_{11} = R_2$
$E_{11} = E_2$

Решение этой системы уравнений (например, методом подстановки) дает нам искомые смешанные величины — потенциал $\phi_1$ и ток $I_K$:

$$ \phi_1 = \frac{E_2 — R_2 J_1}{1 + G_1 R_2} $$
$$ I_K = \frac{G_1 E_2 + J_1}{1 + G_1 R_2} $$

Зная $\phi_1$ и $I_K$, можно найти любые другие параметры схемы. Например, $U_1 = \phi_1$, $I_2 = I_K$, $U_2 = R_2 I_K$ и $I_1 = I_2$.

Примечание: Разбиение на подцепи, показанное на Рис. 1, б) и в), иллюстрирует этот подход. Элемент $G_1$ отнесен к первой подцепи (б), так как он связан с источником тока $J_1$ и описывается через узловой потенциал $\phi_1$. Элемент $R_2$ отнесен ко второй подцепи (в), так как он связан с источником ЭДС $E_2$ и описывается через контурный ток $I_K$.

Преимущества и недостатки метода

Как и любой инженерный подход, МСВ имеет свои сильные и слабые стороны.

Преимущества

Универсальность: Это самый мощный из «ручных» методов, способный рассчитать практически любую линейную цепь, независимо от комбинации источников.
Гибкость: Позволяет аналитику выбрать наиболее удобный набор переменных (потенциалов и токов) для минимизации сложности итоговой системы уравнений.
Основа для САПР: Модифицированные и автоматизированные версии этого метода (например, метод узловых потенциалов с модификациями или метод табличных форм) лежат в основе большинства современных программ-симуляторов схем, таких как SPICE.

Недостатки

Сложность составления уравнений: По сравнению с Методом узловых напряжений или Методом контурных токов , «ручное» формирование системы смешанных уравнений требует большего внимания и аккуратности.
Концептуальная сложность: Требуется четкое понимание, как правильно разделить цепь на подцепи и какие переменные выбрать в качестве базисных.

Сравнение базовых методов анализа цепей

В таблице ниже приведено сравнение трех основных методов анализа линейных цепей.

Метод	Основной закон	Базисные переменные	Неприменим (в чистом виде) для цепей с…
Метод узловых напряжений (МУН)	Первый закон Кирхгофа (закон токов)	Узловые потенциалы (напряжения)	Идеальными источниками ЭДС (напряжения)
Метод контурных токов (МКТ)	Второй закон Кирхгофа (закон напряжений)	Контурные токи	Идеальными источниками тока
Метод смешанных величин (МСВ)	Оба закона Кирхгофа	Набор узловых потенциалов и контурных токов	(Нет ограничений по типу источников)

Интересные факты по теме

Основа SPICE: Большинство всемирно известных симуляторов электронных схем (таких как SPICE, Micro-Cap, Multisim) используют в своем ядре не «чистый» метод узловых напряжений, а его расширенную версию — модифицированный метод узловых напряжений (MNA). MNA, по сути, является формализованным и алгоритмизированным методом смешанных величин.
Связь с теорией управления: Подход МСВ тесно связан с представлением систем в виде «пространства состояний», используемым в теории автоматического управления. Напряжения на конденсаторах и токи через индуктивности (переменные состояния) комбинируются с другими величинами для полного описания системы.
Гибкость выбора: Выбор, какой резистивный элемент к какой подцепи отнести (к «токовой» или «ЭДС»), часто произволен и диктуется удобством. Например, элемент $R_2$ в Примере 1 можно было бы описать как проводимость $G_2 = 1/R_2$ и включить в уравнение для узловых потенциалов. Результат был бы идентичным.
Супер-узлы и супер-контуры: МСВ является более универсальной альтернативой методам «супер-узлов» (применяемым в МУН при наличии источников ЭДС) и «супер-контуров» (применяемым в МКТ при наличии источников тока).
Расширение на нелинейные цепи: Принципы гибридного анализа могут быть расширены и на нелинейные цепи, где уравнения становятся нелинейными и требуют численных методов решения (например, метода Ньютона-Рафсона).

FAQ: Часто задаваемые вопросы

1. Почему нельзя просто использовать метод узловых напряжений (МУН), если в схеме есть источник ЭДС?

Можно, но это усложняет метод. Идеальный источник ЭДС (например, $E_2$ на Рис. 1) фиксирует напряжение между двумя узлами, но ток, протекающий через него, неизвестен. Этот ток нельзя выразить через узловые потенциалы по закону Ома (у источника нет проводимости). Для решения проблемы в МУН вводится концепция «супер-узла», что по сути и является шагом к гибридному методу.

2. Почему нельзя просто использовать метод контурных токов (МКТ), если в схеме есть источник тока?

Аналогичная проблема. Идеальный источник тока (например, $J_1$ на Рис. 1) фиксирует ток в ветви, но напряжение на нем неизвестно. Это напряжение нельзя выразить через контурные токи по закону Ома. В МКТ для этого вводится концепция «супер-контура», что также усложняет «чистый» метод.

3. Метод смешанных величин — это то же самое, что модифицированный узловой анализ (MNA)?

В сущности, да. МСВ — это общее название подхода, а MNA (Modified Nodal Analysis) — это его строго формализованная версия, удобная для составления матриц и компьютерного расчета. В MNA в качестве переменных по умолчанию берутся все узловые потенциалы, а затем к ним добавляются токи через «неудобные» элементы (источники ЭДС, индуктивности), что и делает его гибридным.

4. Что такое «подцепь» в данном контексте? Это физическое разделение?

Нет, это исключительно концептуальное, «бумажное» разделение. Оно используется только на этапе составления системы уравнений, чтобы логически сгруппировать переменные: потенциалы отдельно, токи отдельно. Физически цепь остается единой.

5. Обязательно ли в МСВ число уравнений равно числу источников?

Не обязательно. Число итоговых уравнений в системе равно числу выбранных базисных (независимых) переменных. Этот выбор диктуется топологией цепи. Например, в сложной цепи с одним источником тока и одним источником ЭДС может потребоваться 3 узловых потенциала и 2 контурных тока, что даст систему из 5 уравнений.

Заключение

Метод смешанных величин представляет собой мощный и универсальный инструмент в арсенале инженера-электротехника и студента, изучающего ТОЭ (Теоретические основы электротехники). Он снимает ограничения, присущие «чистым» методам узловых напряжений и контурных токов, позволяя эффективно анализировать сложные схемы с любым сочетанием идеальных источников.

Хотя составление гибридных уравнений вручную может показаться более трудоемким, понимание этого принципа является ключевым для освоения работы современных систем автоматизированного проектирования (САПР) и симуляторов схем, которые используют именно такие гибридные алгоритмы для своей работы.

Нормативная база

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». — Стандарт устанавливает термины и определения базовых понятий в области электротехники, включая «электрическая цепь», «источник ЭДС», «источник тока» и др.