Метод эквивалентного генератора: Расчет электрических цепей

Содержание страницы

1. Понятие двухполюсника
2. Определение и формы эквивалентного генератора
3. Обоснование и определение параметров генератора
4. Взаимное преобразование: Тевенен и Нортон
5. Преимущества, ограничения и сравнение схем
6. Практический пример: Расчет цепи методом эквивалентного генератора
7. Интересные факты по теме
8. Часто задаваемые вопросы (FAQ)
Заключение

Концепция эквивалентного генератора — это основной инструмент в теории электрических цепей (ТОЭ). Что это? По сути, это метод, позволяющий заменить любую, сколь угодно сложную линейную часть электрической цепи, имеющую два вывода (двухполюсник), на простейшую эквивалентную схему. Эта схема состоит всего из одного источника (ЭДС или тока) и одного пассивного элемента (сопротивления или проводимости).

Краткая история: Этот мощный подход был впервые сформулирован французским инженером-телеграфистом Леоном Шарлем Тевененом в 1883 году. Он доказал, что любую линейную активную цепь можно свести к идеальному источнику ЭДС и последовательному ему сопротивлению. Несколько десятилетий спустя, в 1926 году, инженер Bell Labs Эдвард Лори Нортон представил дуальную (двойственную) концепцию — замену той же цепи на идеальный источник тока и параллельную ему проводимость. Эти два подхода, известные сегодня как теоремы Тевенена и Нортона, составляют неразрывную основу метода эквивалентного генератора.

1. Понятие двухполюсника

Чтобы в полной мере освоить метод, необходимо сначала четко определить объект его применения — двухполюсник. В электротехнике двухполюсником называется любая часть электрической цепи, которая имеет два выделенных узла (или «полюса», вывода) для подключения к другим элементам или цепям.

Двухполюсники классифицируются на два основных типа:

Активные двухполюсники: Это двухполюсники, в состав которых входят один или несколько источников электрической энергии (например, источники ЭДС или источники тока). На схемах их условно обозначают прямоугольником с буквой «А» (см. Рис. 1, а).
Пассивные двухполюсники: Это двухполюсники, не содержащие внутренних источников энергии. Они состоят только из пассивных элементов (резисторов, конденсаторов, катушек индуктивности). Их условно обозначают буквой «П».

2. Определение и формы эквивалентного генератора

Эквивалентный генератор — это идеализированная теоретическая модель, которая полностью заменяет сложный активный двухполюсник. Важнейшее свойство этой замены (эквивалентности) заключается в том, что она никак не влияет на распределение токов и напряжений в остальной, внешней части цепи (нагрузке), к которой был подключен исходный двухполюсник.

Эта модель может быть представлена в двух эквивалентных (дуальных) формах:

Схема Тевенена (Эквивалентный генератор ЭДС): Представляет собой последовательное соединение идеального источника ЭДС $E_г$ и внутреннего (эквивалентного) сопротивления $R_г$. Эта схема показана на Рис. 1, б.
Схема Нортона (Эквивалентный генератор тока): Представляет собой параллельное соединение идеального источника тока $J_г$ и внутренней (эквивалентной) проводимости $G_г$. Эта схема показана на Рис. 1, в.

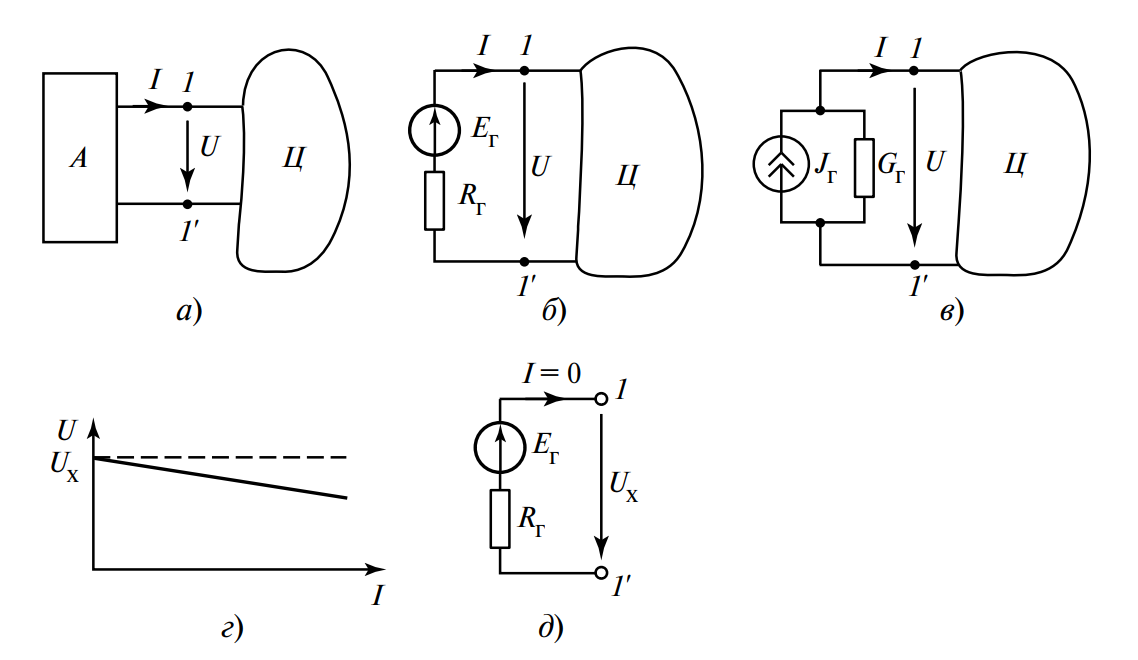
Рис. 1. Эквивалентный генератор двухполюсника:
а) исходная схема: активный двухполюсник (А) и внешняя цепь (Ц);
б) эквивалентный генератор ЭДС (схема Тевенена) для двухполюсника А;
в) эквивалентный генератор тока (схема Нортона) для двухполюсника А;
г) линейная внешняя вольт-амперная характеристика (ВАХ) двухполюсника А;
д) схема для определения напряжения холостого хода $U_х$ двухполюсника А.

3. Обоснование и определение параметров генератора

Правомерность такой замены для линейных электрических цепей строго доказывается на основе принципа суперпозиции (наложения). Поскольку уравнения, описывающие любой линейный активный двухполюсник (составленные по законам Кирхгофа), являются линейными, его внешняя вольт-амперная характеристика (ВАХ) — то есть зависимость напряжения $U$ на выводах 1-1′ от тока $I$, протекающего через них, — также строго линейна.

Эту характеристику можно графически представить в виде наклонной прямой (Рис. 1, г) и описать линейным уравнением:

$$ U = U_х — R \cdot I $$

В этом уравнении два ключевых параметра:

$U_х$ — напряжение холостого хода (ХХ). Это напряжение на выводах 1-1′ двухполюсника, когда внешняя цепь (Ц) отключена (т.е. в режиме холостого хода), и, следовательно, ток $I = 0$ (Рис. 1, д).
$R$ — входное (внутреннее) сопротивление двухполюсника. Это сопротивление «пассивированного» двухполюсника, измеряемое со стороны выводов 1-1′. Для его определения необходимо «обнулить» все независимые источники энергии внутри двухполюсника: все источники ЭДС заменяются коротким замыканием (их R=0), а все источники тока — разрывом цепи (их G=0).

Теперь рассмотрим схему Тевенена (Рис. 1, б). Ее внешняя характеристика, согласно второму закону Кирхгофа для контура, описывается точно таким же по структуре уравнением:

$$ U = E_г — R_г \cdot I $$

Чтобы генератор был полностью эквивалентен исходному двухполюснику, их внешние характеристики $U = f(I)$ должны полностью совпадать. Это достигается при выполнении двух простых условий:

$E_г = U_х$ (ЭДС эквивалентного генератора равна напряжению холостого хода двухполюсника).
$R_г = R$ (Внутреннее сопротивление генератора равно входному сопротивлению пассивированного двухполюсника).

Примечание: Схема эквивалентного генератора ЭДС (Рис. 1, б) и есть то, что в теории цепей называют схемой Тевенена, а сам метод — теоремой Тевенена.

4. Взаимное преобразование: Тевенен и Нортон

Схемы Тевенена и Нортона не являются конкурентами — они абсолютно эквивалентны друг другу и могут быть легко преобразованы одна в другую.

Если мы возьмем уравнение ВАХ для схемы Тевенена $U = E_г — R_г \cdot I$ и выразим из него ток $I$, мы получим:

$$ I = \frac{E_г}{R_г} — \frac{U}{R_г} $$

Это уравнение в точности описывает схему Нортона (Рис. 1, в), где общий ток $I$, вытекающий из вывода 1, равен току источника $J_г$ минус ток, ответвляющийся во внутреннюю проводимость $G_г$ (на которой напряжение равно $U$).

Сравнивая уравнения, мы получаем формулы для преобразования источника ЭДС в источник тока (Тевенена в Нортона):

$$ J_г = \frac{E_г}{R_г} \quad \text{и} \quad G_г = \frac{1}{R_г} $$

(Формула 1)

Разумеется, возможно и обратное преобразование источника тока в источник ЭДС (Нортона в Тевенена). Параметры схемы Тевенена выражаются через параметры схемы Нортона:

$$ E_г = \frac{J_г}{G_г} \quad \text{и} \quad R_г = \frac{1}{G_г} $$

(Формула 2)

Важно: Ток короткого замыкания ($I_{кз}$) двухполюсника (это ток при $U=0$) в точности равен току эквивалентного генератора тока $J_г$. Из уравнения ВАХ: $0 = U_х — R \cdot I_{кз}$, отсюда $I_{кз} = U_х / R = E_г / R_г$, что по формуле (1) и есть $J_г$.

5. Преимущества, ограничения и сравнение схем

Метод эквивалентного генератора (МЭГ) — один из самых востребованных методов расчета, однако важно понимать его сильные и слабые стороны.

Преимущества:

Радикальное упрощение: Метод позволяет заменить чрезвычайно сложную, многоконтурную часть цепи, содержащую множество источников и резисторов, всего двумя элементами.
Анализ нагрузки: Метод идеален для задач, где требуется рассчитать ток, напряжение или мощность только в одной (исследуемой) ветви цепи. Особенно, если параметры этой ветви (нагрузки) меняются. Вместо того чтобы каждый раз пересчитывать всю сложную схему, достаточно один раз найти эквивалентный генератор для «остальной» части цепи.
Наглядность: Упрощенная эквивалентная схема (Рис. 1, б или в) делает физическую картину процессов в цепи гораздо более понятной.

Недостатки и ограничения:

Только для линейных цепей: Метод неприменим, если в «сворачиваемой» части цепи есть нелинейные элементы (например, диоды, транзисторы, варисторы).
Потеря внутренней информации: При замене двухполюсника на генератор мы полностью теряем информацию о токах и напряжениях внутри самого двухполюсника. Метод позволяет найти параметры только во внешней, неэквивалентной части цепи.
Сложность расчета параметров: В некоторых случаях определение $U_х$ и $R_г$ само по себе может быть нетривиальной задачей, требующей расчета сложной цепи (хотя и в двух более простых режимах: холостого хода и с «выключенными» источниками).

Сравнительная таблица: Тевенен vs Нортон

Характеристика	Схема Тевенена	Схема Нортона
Тип источника	Идеальный источник ЭДС (Напряжения)	Идеальный источник тока
Внутренний элемент	Сопротивление $R_г$ (Ом)	Проводимость $G_г$ (Сименс)
Схема соединения	Последовательное	Параллельное
Расчетный параметр источника	Равен напряжению холостого хода $U_х$	Равен току короткого замыкания $I_{кз}$
Расчетный пассивный параметр	$R_г = R_{вх}$	$G_г = 1 / R_{вх}$
Предпочтительное применение	Удобнее при последовательном соединении с нагрузкой (анализ по 2-му закону Кирхгофа)	Удобнее при параллельном соединении с нагрузкой (анализ по 1-му закону Кирхгофа)

6. Практический пример: Расчет цепи методом эквивалентного генератора

Задача: Найти параметры эквивалентного генератора (Тевенена) для двухполюсника, выделенного на Рис. 2, а штриховой линией. Используя полученный генератор, рассчитать ток $I$ во внешней ветви.

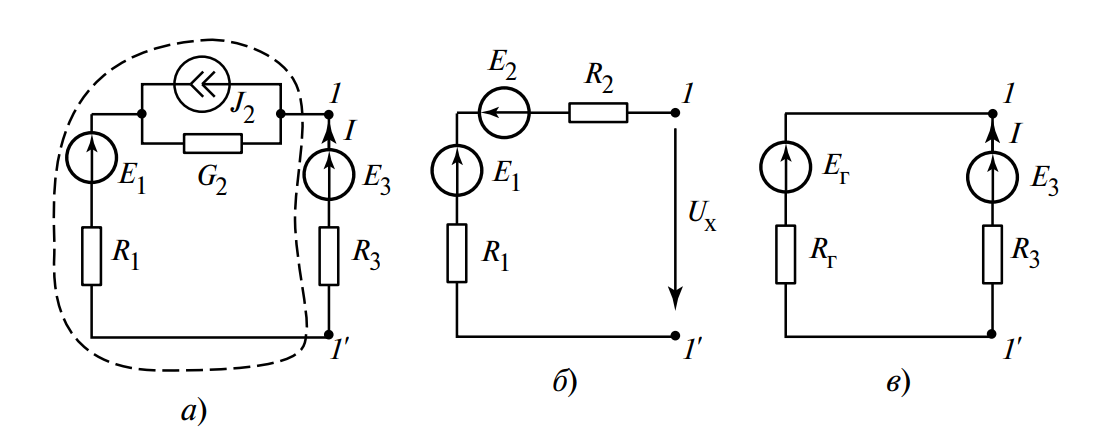
Рис. 2. Расчет цепи методом эквивалентного генератора:
а) исходная электрическая схема;
б) схема для определения напряжения холостого хода $U_х$ после преобразования источника тока;
в) итоговая простейшая цепь с эквивалентным генератором.

Шаг 1: Преобразование схемы для удобства расчета

В исходной схеме (Рис. 2, а) имеется источник тока $J_2 = 1$ A с параллельной ему проводимостью $G_2 = 0.5$ См. Для упрощения дальнейших расчетов (особенно $U_х$) преобразуем этот узел (генератор Нортона) в эквивалентный генератор ЭДС (схему Тевенена) по формулам (2):

ЭДС нового источника: $E_2 = J_2 / G_2 = 1 \text{ А} / 0.5 \text{ См} = 2 \text{ В}$
Сопротивление: $R_2 = 1 / G_2 = 1 / 0.5 \text{ См} = 2 \text{ Ом}$

Получаем преобразованную схему двухполюсника, показанную на Рис. 2, б.

Шаг 2: Определение напряжения холостого хода $U_х$

Рассмотрим схему на Рис. 2, б в режиме холостого хода (выводы 1-1′ разомкнуты). В этом режиме ток во всей цепи (включая $R_1$ и $R_2$) равен нулю ($I_{XX} = 0$). Следовательно, падения напряжения на сопротивлениях $R_1$ и $R_2$ отсутствуют ($U_{R1} = 0$, $U_{R2} = 0$).

Напряжение $U_х$ на выводах 1-1′ будет равно алгебраической сумме ЭДС в этом (разомкнутом) контуре. По второму закону Кирхгофа:

$U_х = U_{11′} = E_1 — E_2$

Согласно данным из оригинального примера, результат этого вычисления: $U_х = 1 \text{ В}$.

Таким образом, ЭДС эквивалентного генератора: $E_г = U_х = 1 \text{ В}$.

Шаг 3: Определение внутреннего сопротивления $R_г$

Для определения входного сопротивления $R$ (которое равно $R_г$) мысленно «пассивируем» схему на Рис. 2, б: «выключаем» все независимые источники ЭДС $E_1$ и $E_2$, заменяя их коротким замыканием (перемычками).

Глядя на схему со стороны выводов 1-1′, мы видим два последовательно соединенных сопротивления $R_1$ и $R_2$.

$R_г = R = R_1 + R_2$

Согласно данным из оригинального примера, результат этого сложения: $R = 5 \text{ Ом}$.

Таким образом, внутреннее сопротивление эквивалентного генератора: $R_г = R = 5 \text{ Ом}$.

Шаг 4: Расчет тока $I$ в результирующей цепи

Теперь мы заменяем весь сложный двухполюсник (в штриховой рамке на Рис. 2, а) на его только что найденный эквивалентный генератор (схему Тевенена) с параметрами $E_г = 1 \text{ В}$ и $R_г = 5 \text{ Ом}$.

Мы получаем простейшую неразветвленную цепь, показанную на Рис. 2, в, состоящую из нашего эквивалентного генератора и нагрузки ($R_3$, $E_3$).

Расчет тока $I$ в этой неразветвленной цепи не вызывает сложностей и может быть проведен по обобщенному закону Ома для замкнутого контура:

$$ I = \frac{\sum E}{\sum R} = \frac{E_г — E_3}{R_г + R_3} $$

Подставляя значения из оригинального примера (где $E_3 = -1.5 \text{ В}$ и $R_3 = 0 \text{ Ом}$), получаем:

$$ I = \frac{1 \text{ В} — (-1.5 \text{ В})}{5 \text{ Ом} + 0 \text{ Ом}} = \frac{2.5 \text{ В}}{5 \text{ Ом}} = 0.5 \text{ А} $$

Вывод по примеру: Этот расчет наглядно демонстрирует мощь метода. Вместо решения системы уравнений Кирхгофа для исходной сложной схемы (Рис. 2, а), мы свели задачу к трем простым шагам: расчету $U_х$, расчету $R_г$ и расчету тока в элементарном контуре.

Подход, основанный на замене отдельных сложных подцепей (двухполюсников) на их более простые эквивалентные модели (генераторы), является частью более общего методологического подхода, известного как диакоптика, или метод расчета электрических цепей по частям.

7. Интересные факты по теме

Теорема двойственности: Теоремы Тевенена и Нортона являются идеальным примером принципа двойственности в теории цепей. Все, что справедливо для напряжений, ЭДС и последовательных соединений (Тевенен), имеет свой «зеркальный» аналог для токов, источников тока и параллельных соединений (Нортон).
Не только резисторы: Метод полностью применим для цепей переменного тока (AC). В этом случае вместо сопротивлений ($R_г$) используются комплексные импедансы ($Z_г$), а вместо ЭДС ($E_г$) — комплексные амплитуды напряжений ($\dot{E}_г$). Все формулы сохраняют свою структуру, но расчеты ведутся в комплексной плоскости.
Экспериментальное определение: Параметры $E_г$ и $R_г$ можно найти чисто экспериментально, не зная «внутренностей» двухполюсника. Для этого достаточно двух измерений: напряжения холостого хода ($U_х = E_г$) вольтметром и тока короткого замыкания ($I_{кз} = J_г$) амперметром. Тогда $R_г = U_х / I_{кз}$.
Предшественник Тевенена: Немецкий физик Герман фон Гельмгольц сформулировал аналогичную теорему еще в 1853 году (за 30 лет до Тевенена). Однако работа Тевенена была более общей и сфокусированной именно на анализе электрических цепей.
Согласование нагрузки: Из теоремы Тевенена напрямую следует фундаментальная теорема о максимальной мощности. Нагрузка, подключенная к двухполюснику, будет потреблять максимальную мощность, когда ее сопротивление равно внутреннему сопротивлению генератора ($R_{нагрузки} = R_г$).

8. Часто задаваемые вопросы (FAQ)

1. В чем разница между эквивалентным генератором и реальным (например, батарейкой)?

Реальный источник (батарейка) — это физический объект. Эквивалентный генератор — это теоретическая модель. Эта модель может описывать не только одну батарейку, но и целую электростанцию или сложную плату с десятками компонентов, «свернутую» в один простой эквивалент для расчета внешней цепи. Модель реальной батарейки часто представляют в виде схемы Тевенена (идеальная ЭДС и внутреннее R), но эквивалентный генератор — понятие гораздо более широкое.

2. Можно ли использовать метод эквивалентного генератора для цепей с конденсаторами и катушками?

Да, абсолютно. Как упомянуто выше (факт 2), в этом случае расчет ведется для цепей переменного тока (AC) с использованием комплексных чисел. Вместо сопротивлений ($R$) используются комплексные импедансы ($Z$), которые учитывают емкостное ($Z_C = 1 / (j\omega C)$) и индуктивное ($Z_L = j\omega L$) сопротивления. Все формулы остаются верными, но расчеты (сложение, деление) производятся по правилам работы с комплексными числами.

3. Что делать, если в двухполюснике есть зависимые (управляемые) источники?

Метод остается применим, но с важной оговоркой: «выключать» (обнулять) зависимые источники при расчете $R_г$ нельзя, так как их поведение зависит от токов и напряжений в самой схеме. В этом случае $R_г$ находят одним из двух способов:
1. Через холостой ход и короткое замыкание: $R_г = U_х / I_{кз}$.
2. Методом «тестового источника»: «выключают» все независимые источники, к выводам 1-1′ подключают тестовый источник (например, $U_т = 1 \text{ В}$) и находят ток $I_т$, который он отдает в схему. Тогда $R_г = U_т / I_т$.

4. Что такое «входное сопротивление» пассивного двухполюсника?

Это общее (эквивалентное) сопротивление двухполюсника, не содержащего источников энергии, измеренное на его выводах. Если двухполюсник был активным, то его «входное сопротивление» — это сопротивление, которое он имеет после «выключения» (обнуления) всех его внутренних независимых источников (ЭДС -> КЗ, Источники тока -> Разрыв). Именно это сопротивление и используется в качестве $R_г$.

5. Какую схему в итоге выбрать: Тевенена или Нортона?

Выбор диктуется исключительно удобством дальнейшего расчета. Они полностью взаимозаменяемы. Практическое правило: если нагрузка подключается к двухполюснику последовательно, удобнее использовать схему Тевенена (получается один простой контур). Если нагрузка подключается параллельно, удобнее схема Нортона (получается один простой узел для расчета по первому закону Кирхгофа).

Заключение

Метод эквивалентного генератора, объединяющий теоремы Тевенена и Нортона, является краеугольным камнем в анализе линейных электрических цепей. Он предоставляет инженерам, техникам и студентам мощнейший инструмент для декомпозиции и упрощения сложных систем. Позволяя «свернуть» любую сколь угодно запутанную часть цепи до одного источника и одного пассивного элемента, этот метод кардинально упрощает расчеты токов, напряжений и мощностей в конкретной, интересующей нас ветви (нагрузке). Глубокое понимание этого метода необходимо для успешного освоения всех последующих разделов электротехники, электроники и радиотехники.

Нормативная база

Основные термины, определения и графические обозначения, используемые при анализе электрических цепей, регламентируются действующими стандартами, в том числе:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий.» (Устанавливает общие термины и определения для области электротехники).
ГОСТ 2.721-74 «Единая система конструкторской документации. Обозначения условные графические в схемах. Обозначения общего применения.» (Регламентирует условные графические обозначения элементов на схемах, аналогичных Рис. 1 и 2).

Метод эквивалентного генератора в теории электрических цепей