Метод эквивалентного генератора: теория, расчет и примеры

Содержание страницы

Теоретические основы метода
Алгоритм расчета цепи методом эквивалентного генератора
Экспериментальное определение параметров
Сравнение методов эквивалентного генератора напряжения и тока
Преимущества и ограничения метода
Примеры расчетов
Интересные факты о методе эквивалентного генератора
Часто задаваемые вопросы (FAQ)
Заключение

Метод эквивалентного генератора (МЭГ) является одним из фундаментальных методов расчета сложных линейных электрических цепей. В отечественной и зарубежной технической литературе он также известен как теорема Тевенена (Thévenin’s theorem), а в варианте с источником тока — как теорема Нортона. Данный метод позволяет существенно упростить анализ цепи, когда необходимо определить ток или напряжение только в одной ее ветви, заменяя остальную, сколь угодно сложную часть схемы, простейшим эквивалентом.

Историческая справка: Впервые теорема была сформулирована немецким физиком Германом фон Гельмгольцем в 1853 году. Позднее, в 1883 году, она была независимо «переоткрыта» французским телеграфным инженером Леоном Шарлем Тевененом. В 1926 году инженер Bell Labs Эдвард Лорри Нортон дополнил ее, предложив эквивалентную схему с источником тока. В современной российской инженерной практике принят обобщающий термин «метод эквивалентного генератора».

Теоретические основы метода

Любую часть сложной электрической схемы, имеющую два выделенных зажима (полюса) для подключения к остальной части цепи, называют двухполюсником. Согласно ГОСТ Р 52002-2003, двухполюсники подразделяются на:

Активные (АД): содержат внутри себя источники электрической энергии (ЭДС или тока).
Пассивные (ПД): не содержат источников энергии, либо действие всех источников взаимно скомпенсировано.

Суть метода заключается в следующем: по отношению к любой выделенной ветви вся остальная активная часть схемы может быть заменена эквивалентным реальным источником напряжения (генератором). Этот эквивалентный генератор характеризуется двумя основными параметрами:

ЭДС эквивалентного генератора ($E_э$) — равна напряжению холостого хода ($U_{xx}$) на разомкнутых зажимах активного двухполюсника.
Внутреннее сопротивление ($R_э$) — равно входному сопротивлению пассивного двухполюсника со стороны этих зажимов при условии, что все независимые источники внутри двухполюсника выключены (источники ЭДС закорочены, источники тока разомкнуты).

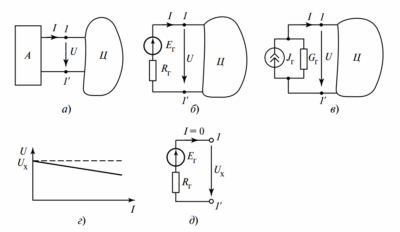
Рисунок 1. Двухполюсники: а — активный; б — с нагрузкой; в — преобразование к эквивалентному генератору

На рисунке 1 показан принцип эквивалентирования. Активный двухполюсник (рис. 1а) при подключении нагрузки (рис. 1б) заменяется простой последовательной цепью (рис. 1в), состоящей из $E_э$ и $R_э$.

Математическое обоснование

Рассмотрим схему (рис. 1б), где к активному двухполюснику присоединена ветвь с сопротивлением $R$, и в ней протекает искомый ток $I$. Согласно принципу компенсации, мы можем включить в эту ветвь две идеальные ЭДС, равные по величине и направленные встречно, что не изменит режим работы цепи. Если принять величину этих ЭДС равной напряжению холостого хода $U_{xx}$ на зажимах двухполюсника, то, используя принцип наложения, можно доказать, что ток в ветви определяется формулой:

$$ I = \frac{E_э}{R_э + R} $$

где $E_э = U_{xx}$. Это уравнение является базовым для расчета цепей данным методом.

Алгоритм расчета цепи методом эквивалентного генератора

Для практического применения метода рекомендуется придерживаться следующей строгой последовательности действий:

Выделение ветви: Мысленно или на схеме отключить ветвь, в которой требуется найти ток. Оставшаяся часть цепи рассматривается как активный двухполюсник.
Расчет $U_{xx}$ (ЭДС $E_э$): Рассчитать напряжение на разомкнутых зажимах полученного двухполюсника любым известным методом (Метод контурных токов, метод узловых напряжений, законы Кирхгофа). Это напряжение равно $E_э$.
Расчет $R_э$: Определить эквивалентное сопротивление двухполюсника относительно разомкнутых зажимов. При этом все источники ЭДС в схеме двухполюсника заменяются короткими замыканиями, а источники тока — разрывами цепи.
Составление эквивалентной схемы: Нарисовать одноконтурную схему, содержащую найденные $E_э$, $R_э$ и ранее отключенную ветвь $R$.
Определение искомого тока: Рассчитать ток по закону Ома для полной цепи.

Экспериментальное определение параметров

Параметры эквивалентного генератора могут быть определены не только расчетным, но и опытным путем, что особенно ценно при работе с «черным ящиком» — устройством, внутренняя структура которого неизвестна или слишком сложна.

Опыт холостого хода: Измеряется вольтметром с высоким внутренним сопротивлением напряжение на разомкнутых зажимах. Полученное значение соответствует $E_э$.
Опыт короткого замыкания: Зажимы замыкаются накоротко через амперметр (чье сопротивление пренебрежимо мало), измеряется ток $I_{кз}$.

Внутреннее сопротивление рассчитывается как:

$$ R_э = \frac{U_{xx}}{I_{кз}} = \frac{E_э}{I_{кз}} $$

Важно: В мощных промышленных цепях опыт короткого замыкания может быть аварийным и недопустимым. В таких случаях применяют метод известной нагрузки: подключают резистор известного номинала $R_{нагр}$, измеряют ток $I_{нагр}$ или напряжение $U_{нагр}$, и вычисляют $R_э$ из уравнения: $ R_э = \frac{U_{xx} — U_{нагр}}{I_{нагр}} $.

Сравнение методов эквивалентного генератора напряжения и тока

Существует дуальный вариант метода — использование эквивалентного генератора тока (теорема Нортона). Выбор между ними зависит от топологии конкретной схемы.

Таблица 1. Сравнение эквивалентных схем Тевенена и Нортона
Характеристика	Эквивалент напряжения (Тевенен)	Эквивалент тока (Нортон)
Базовый элемент	Идеальный источник ЭДС ($E_э$)	Идеальный источник тока ($J_э$)
Схема замещения	Последовательное соединение $E_э$ и $R_э$	Параллельное соединение $J_э$ и $G_э$ (проводимость)
Основной параметр источника	$E_э = U_{xx}$ (напряжение холостого хода)	$J_э = I_{кз}$ (ток короткого замыкания)
Внутренний параметр	Сопротивление $R_э$	Проводимость $G_э = 1/R_э$
Предпочтительное применение	Цепи с последовательным включением нагрузок, высокое внутреннее сопротивление	Цепи с параллельными ветвями, низкое внутреннее сопротивление

Преимущества и ограничения метода

Преимущества:

Эффективность при вариации нагрузки: Идеален, когда нужно исследовать поведение одной ветви при изменении ее параметров, не пересчитывая всю остальную цепь.
Упрощение сложных схем: Позволяет свернуть громоздкую часть цепи в два элемента.
Применимость к «черным ящикам»: Позволяет моделировать реальные устройства (аккумуляторы, усилители) по результатам внешних измерений.

Недостатки:

Потеря информации о внутренних процессах: Эквивалентная схема не отражает распределение токов и мощностей внутри исходного активного двухполюсника.
Некорректность энергетического баланса: Мощность, рассеиваемая на $R_э$, не равна суммарной мощности потерь внутри исходной цепи.
Ограничение линейностью: Метод в классическом виде применим только к линейным цепям (или линеаризованным на рабочем участке).

Примеры расчетов

Пример 1: Расчет мостовой схемы

Задача: Определить ток в диагонали мостовой схемы (резистор $R_5$), представленной на рисунке 2а.

Дано: $R_1 = R_4 = 1$ Ом; $R_2 = 4$ Ом; $R_3 = R_5 = 3$ Ом; $E_1 = 10$ В.

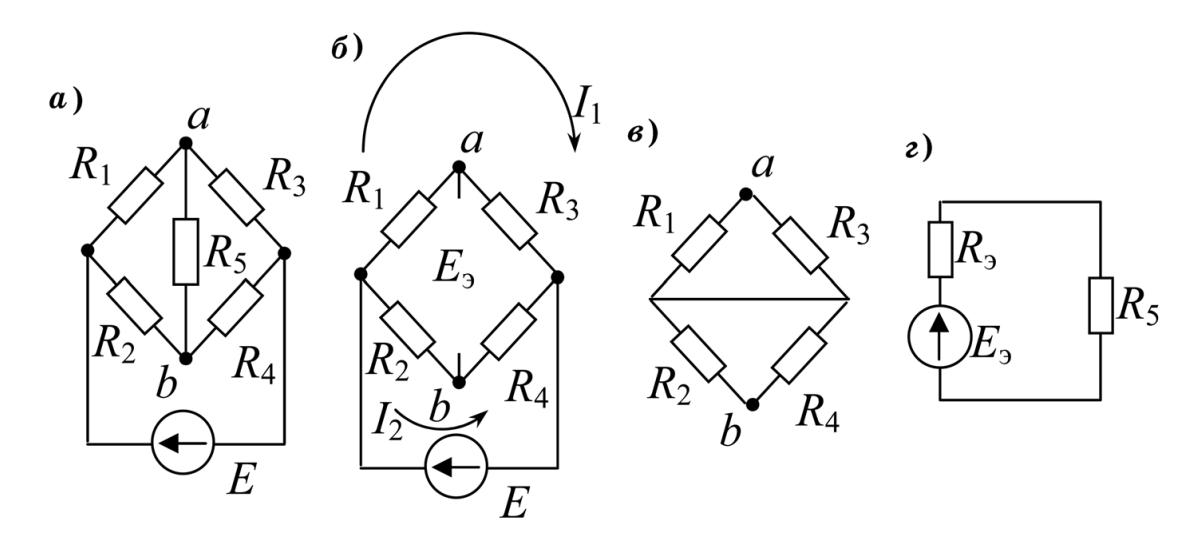
Рисунок 2. Этапы расчета мостовой схемы: а — исходная схема; б — определение $E_э$; в — определение $R_э$; г — схема с эквивалентным генератором.

Решение:

Определение $E_э$: Отключаем ветвь с $R_5$ (рис. 2б). Напряжение холостого хода $U_{ab(xx)}$ между точками подключения диагонали найдем, определив токи в ветвях моста. Так как ветвь разомкнута, токи $I_1$ и $I_2$ протекают через последовательно соединенные пары резисторов:
$$ I_1 = \frac{E_1}{R_1 + R_3} = \frac{10}{1 + 3} = 2,5 \text{ А} $$
$$ I_2 = \frac{E_1}{R_2 + R_4} = \frac{10}{4 + 1} = 2 \text{ А} $$
По второму закону Кирхгофа для контура, образованного $R_3$, $R_4$ и разомкнутыми зажимами a-b:
$$ U_{ab(xx)} + I_2 R_4 — I_1 R_3 = 0 $$
$$ E_э = U_{ab(xx)} = I_1 R_3 — I_2 R_4 = 2,5 \cdot 3 — 2 \cdot 1 = 7,5 — 2 = 5,5 \text{ В} $$
Определение $R_э$: Исключаем источник ЭДС $E_1$ (закорачиваем его). Схема превращается в две параллельные ветви, соединенные последовательно относительно зажимов a и b (рис. 2в):
$$ R_э = \frac{R_1 R_3}{R_1 + R_3} + \frac{R_2 R_4}{R_2 + R_4} = \frac{1 \cdot 3}{1 + 3} + \frac{4 \cdot 1}{4 + 1} = 0,75 + 0,8 = 1,55 \text{ Ом} $$
Расчет тока: Собираем эквивалентную схему (рис. 2г) и находим ток в $R_5$:
$$ I_5 = \frac{E_э}{R_э + R_5} = \frac{5,5}{1,55 + 3} \approx 1,21 \text{ А} $$

Пример 2: Определение параметров «черного ящика»

Задача: В схеме на рисунке 3 неизвестна внутренняя структура активного двухполюсника, но известны показания приборов. Вольтметр показывает $U = 100$ В. При его коротком замыкании амперметр показывает $I_{кз} = 10$ А. Определить ток, если вместо вольтметра подключить резистор $R = 30$ Ом.

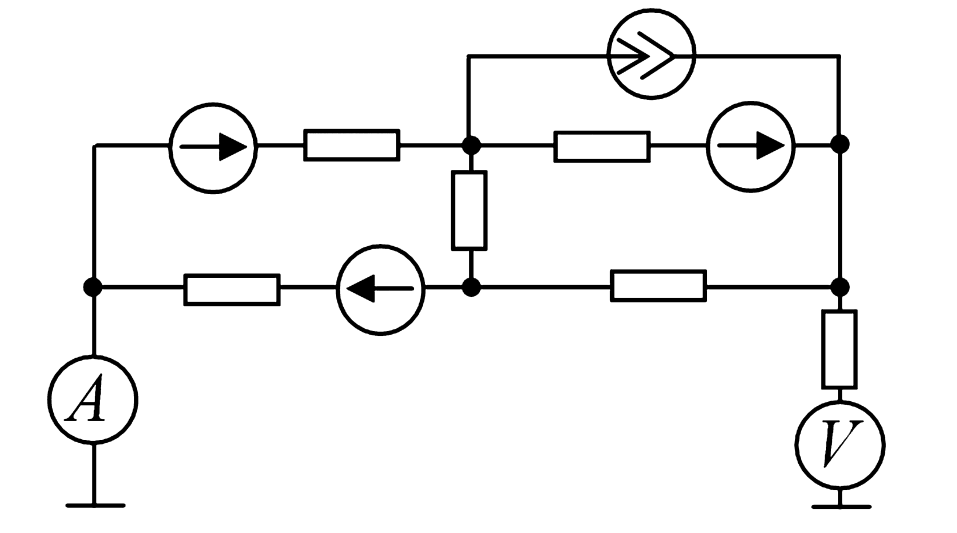
Схема с активным двухполюсником и подключенными измерительными приборами.

Рисунок 3. Исходная схема с неизвестным двухполюсником к примеру 2.

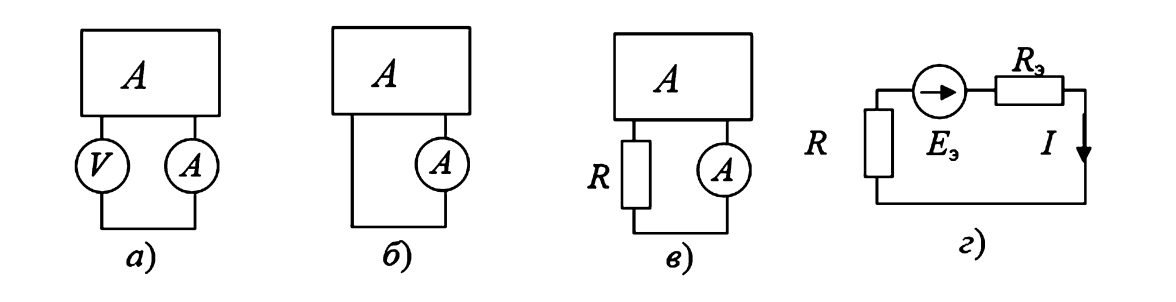
Преобразование схемы: а — опыт холостого хода; б — опыт короткого замыкания; в — рабочий режим; г — расчетная эквивалентная схема.

Рисунок 4. Преобразование схемы: а — опыт холостого хода; б — опыт короткого замыкания; в — рабочий режим; г — расчетная эквивалентная схема.

Решение:

Идеальный вольтметр имеет бесконечное сопротивление, поэтому его показание соответствует напряжению холостого хода (рис. 4а): $E_э = U_{xx} = 100$ В.
Показание амперметра при закорачивании выхода соответствует току короткого замыкания (рис. 4б): $I_{кз} = 10$ А.
Вычисляем внутреннее эквивалентное сопротивление:
$$ R_э = \frac{U_{xx}}{I_{кз}} = \frac{100}{10} = 10 \text{ Ом} $$
При подключении нагрузки $R = 30$ Ом (рис. 4в), переходим к эквивалентной схеме (рис. 4г) и находим ток:
$$ I = \frac{E_э}{R_э + R} = \frac{100}{10 + 30} = \frac{100}{40} = 2,5 \text{ А} $$

Интересные факты о методе эквивалентного генератора

Двойное открытие: Теорема была открыта Гельмгольцем за 30 лет до Тевенена, но именно публикация Тевенена сделала ее широко известной в инженерных кругах.
Универсальность: Метод применим не только к цепям постоянного тока, но и к цепям переменного синусоидального тока (с использованием комплексных чисел $Z_э$, $\dot{E}_э$).
Аудиоинженерия: Понятия «выходной импеданс» усилителя и «входной импеданс» динамика — это прямые следствия применения данной теоремы для согласования устройств.
Биоэлектричество: В физиологии эквивалентные схемы Тевенена используются для моделирования нервных клеток и прохождения сигналов через мембраны.
Максимальная мощность: Теорема лежит в основе условия передачи максимальной мощности от источника в нагрузку (достигается при $R_{нагр} = R_э$).
Ограничение по частоте: В цепях СВЧ понятие двухполюсника усложняется из-за волновых процессов, и метод применяют с осторожностью, используя S-параметры.
Диагностика: Метод используется для диагностики старения химических источников тока (аккумуляторов) путем отслеживания роста их $R_э$ со временем.

Часто задаваемые вопросы (FAQ)

1. Можно ли применять метод к нелинейным цепям?

Напрямую — нет. Метод строго справедлив только для линейных цепей. Однако, если нелинейная цепь работает в режиме малого сигнала, ее можно линеаризовать в рабочей точке и применить метод для приращений.

2. Равна ли мощность, выделяемая в эквивалентном генераторе, мощности в исходной цепи?

Нет, это распространенное заблуждение. Эквивалентная схема моделирует только поведение на внешних зажимах. Внутреннее потребление мощности в ней и в реальной схеме различается.

3. Что делать, если в схеме есть зависимые источники?

При расчете $R_э$ зависимые источники нельзя просто «выключать». Необходимо либо использовать метод пробного источника (подключить внешний источник к зажимам и найти отношение $U/I$), либо рассчитывать $U_{xx}$ и $I_{кз}$ непосредственно, тогда $R_э = U_{xx} / I_{кз}$.

4. Как быть, если Rэ оказалось отрицательным?

В цепях с зависимыми источниками (например, электронные схемы с транзисторами, операционными усилителями с ПОС) эквивалентное сопротивление действительно может быть отрицательным. Это указывает на потенциальную неустойчивость активной цепи.

5. В чем разница между ЭДС и напряжением холостого хода в контексте метода?

В контексте метода эти понятия численно равны. $U_{xx}$ — это измеряемая или вычисляемая разность потенциалов на разомкнутых зажимах, которая затем присваивается параметру $E_э$ модельного источника.

6. Всегда ли можно найти ток короткого замыкания?

Теоретически для линейных схем — да. На практике некоторые активные двухполюсники могут выйти из строя при реальном коротком замыкании, поэтому используют экстраполяцию нагрузочной характеристики.

7. Как метод работает в трехфазных цепях?

Он применим для расчета несимметричных режимов (например, однофазного КЗ). Вся симметричная часть системы заменяется эквивалентным генератором относительно точки аварии.

Заключение

Метод эквивалентного генератора является мощным инструментом в арсенале инженера-электрика. Он позволяет абстрагироваться от излишней сложности внутренней структуры цепи, фокусируясь на взаимодействии источника и нагрузки. Понимание этого метода необходимо не только для ручных расчетов, но и для грамотной интерпретации результатов компьютерного моделирования сложных электротехнических и электронных систем.

Нормативная база

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий.
ГОСТ 2.702-2011 — Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем.
ГОСТ IEC 60050-131-2015 — Международный электротехнический словарь. Часть 131. Теория цепей.
ГОСТ 19880-74 — Электротехника. Основные понятия. Термины и определения (архивный, но часто используемый в фундаментальной литературе).

Список рекомендуемой литературы

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2023.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Том 1. — СПб.: Питер, 2019.
Шевелев В.Е. Основы теории электрических цепей: Учебное пособие. — М.: ФОРУМ: ИНФРА-М, 2021.