Метод двух узлов: расчет электрических цепей, формулы и примеры

Содержание страницы

1. Теоретические основы
2. Практические примеры расчета
3. Сравнительный анализ методов расчета
4. Преимущества и недостатки метода
5. Интересные факты о методе двух узлов
6. FAQ: Часто задаваемые вопросы
Заключение

Метод двух узлов (в зарубежной литературе часто упоминается как теорема Миллмана) представляет собой частный, но широко распространенный случай метода узловых потенциалов. Он применяется для электрических схем, которые содержат всего два узла и произвольное количество параллельных ветвей, соединяющих эти узлы.

Согласно ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий», узел электрической цепи — это место соединения трех и более ветвей. Ситуации, когда вся сложная схема сводится к двум таким узлам, часто встречаются в системах электроснабжения (например, параллельная работа нескольких генераторов на общую нагрузку) или в электронике (питание множества блоков от общей шины).

Введение в проблематику: В современной электротехнике скорость и точность расчетов имеют критическое значение. Классическое применение законов Кирхгофа для многоконтурных цепей часто приводит к громоздким системам уравнений. Метод двух узлов является эффективным инструментом, позволяющим свести расчет сложной разветвленной цепи с двумя общими точками к одному линейному уравнению.

1. Теоретические основы

1.1. Вывод основной расчетной формулы

Рассмотрим схему, имеющую два узла: 1 и 2. Примем потенциал одного из узлов равным нулю (заземлим его), например, $\phi_2 = 0$. В этом случае напряжение между узлами $U_{12}$ будет равно потенциалу первого узла:

$$U_{12} = \phi_1 — \phi_2 = \phi_1 — 0 = \phi_1$$

Используя первый закон Кирхгофа для узла 1, сумма всех токов, втекающих в узел, должна быть равна сумме вытекающих. В методе узловых потенциалов это записывается через проводимости ветвей $g_k = 1/R_k$.

Базовое уравнение метода узловых потенциалов для первого узла:

$$\phi_1 \cdot g_{11} = J_{1\text{пр}}$$

Где:

$g_{11} = \sum g_k$ — собственная узловая проводимость узла 1, равная сумме проводимостей всех ветвей, присоединенных к этому узлу.
$J_{1\text{пр}} = \sum \pm E_k g_k + \sum \pm J_k$ — узловой ток, равный алгебраической сумме произведений ЭДС ветвей на их проводимости и токов источников тока.

Из этого следует итоговая формула метода двух узлов для определения межузлового напряжения:

$$U_{12} = \frac{\sum_{k=1}^{n} E_k g_k + \sum_{m=1}^{j} J_m}{\sum_{k=1}^{n} g_k} \quad (1)$$

Важно (правило знаков): В формуле (1) слагаемое $E_k g_k$ берется со знаком «плюс», если ЭДС $E_k$ направлена к узлу 1, и со знаком «минус», если от него. Аналогично, ток источника тока $J_m$ берется с «плюсом», если он направлен к узлу 1.

После нахождения $U_{12}$ токи в отдельных ветвях определяются по второму закону Кирхгофа или закону Ома для активного участка цепи:

$$I_k = (E_k — U_{12}) \cdot g_k$$

2. Практические примеры расчета

2.1. Пример 1: Базовый расчет разветвленной цепи

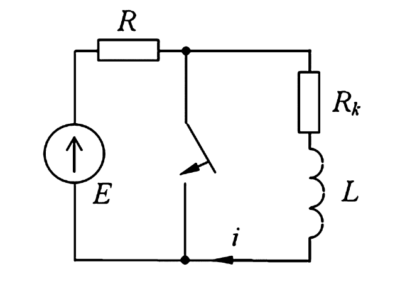
Задача: Определить токи в схеме, если известны параметры элементов: $R_1 = 2$ Ом, $R_2 = 1$ Ом, $R_3 = 4$ Ом, $E_1 = 8$ В, $E_2 = 6$ В, $J = 5,5$ А.

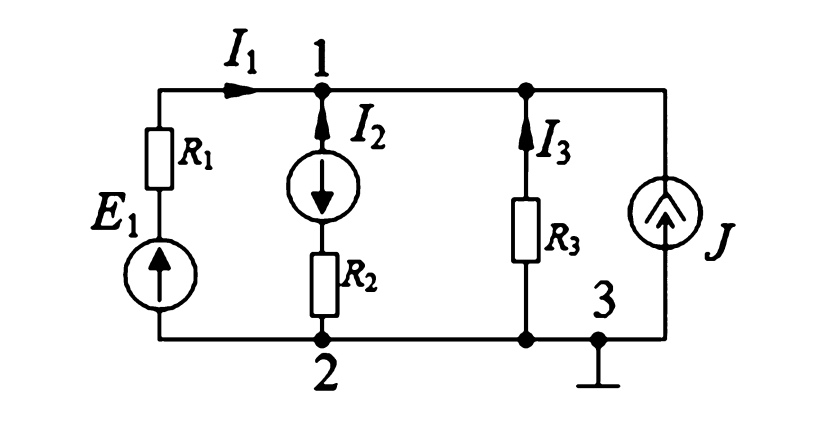
Рисунок 1. Расчетная схема электрической цепи с двумя узлами

На схеме изображены два узла: верхний 1 и нижний 2. Между ними включены четыре параллельные ветви. Первая ветвь содержит E1 и R1, ЭДС направлена вверх к узлу 1. Вторая ветвь содержит E2 и R2, ЭДС направлена вниз от узла 1. Третья ветвь содержит только резистор R3. Четвертая ветвь — источник тока J, направленный вверх к узлу 1.

Решение:

Выбор опорного узла: Заземлим нижний узел 2 ($\phi_2 = 0$). Положительные направления искомых токов в ветвях с резисторами зададим от узла 2 к узлу 1 (или наоборот, в зависимости от принятой конвенции в конкретном задачнике, здесь примем направления к верхнему узлу 1 для источников и от него для пассивных элементов для стандартной записи, но будем следовать знакам из исходных данных).Уточнение по исходным данным: судя по уравнению баланса, $E_1$ направлена к узлу 1, $E_2$ направлена от узла 1, $J$ направлен к узлу 1.
Расчет межузлового напряжения: Применим формулу (1).
$$U_{12} = \frac{E_1 g_1 — E_2 g_2 + J}{g_1 + g_2 + g_3} = \frac{8 \cdot (1/2) — 6 \cdot (1/1) + 5.5}{1/2 + 1/1 + 1/4}$$
$$U_{12} = \frac{4 — 6 + 5.5}{0.5 + 1 + 0.25} = \frac{3.5}{1.75} = 2 \text{ В}$$
Определение токов ветвей:
$$I_1 = (E_1 — U_{12}) \cdot g_1 = (8 — 2) \cdot 0.5 = 3 \text{ А}$$
$$I_2 = (-E_2 — U_{12}) \cdot g_2 = (-6 — 2) \cdot 1 = -8 \text{ А}$$
(Знак «минус» означает, что реальный ток течет противоположно выбранному положительному направлению, т.е. к узлу 2).
$$I_3 = (0 — U_{12}) \cdot g_3 = (0 — 2) \cdot 0.25 = -0.5 \text{ А}$$
Проверка (баланс мощностей):
Баланс генерируемой и потребляемой мощности подтверждает правильность расчета.
$$P_{\text{ист}} = E_1 I_1 + E_2 I_{2\text{факт}} + U_{12} J = 8 \cdot 3 + (-6) \cdot (-8) + 2 \cdot 5.5 = 24 + 48 + 11 = 83 \text{ Вт}$$
$$P_{\text{потр}} = I_1^2 R_1 + I_2^2 R_2 + I_3^2 R_3 = 3^2 \cdot 2 + (-8)^2 \cdot 1 + (-0.5)^2 \cdot 4 = 18 + 64 + 1 = 83 \text{ Вт}$$
Баланс сошелся: $83 \text{ Вт} = 83 \text{ Вт}$.

2.2. Пример 2: Анализ системы электрооборудования автомобиля

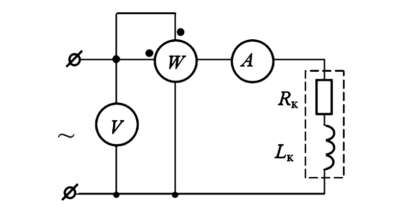
Задача: В бортовой сети автомобиля параллельно включены два источника: аккумулятор ($E_2 = 13$ В, $R_2 = 0,02$ Ом) и генератор ($E_1$ изменяется от 0 до 15 В, $R_1 = 0,04$ Ом). К ним подключено множество потребителей, которые можно заменить одним эквивалентным сопротивлением $R$. Необходимо исследовать режимы работы при разных $E_1$ и $R$.

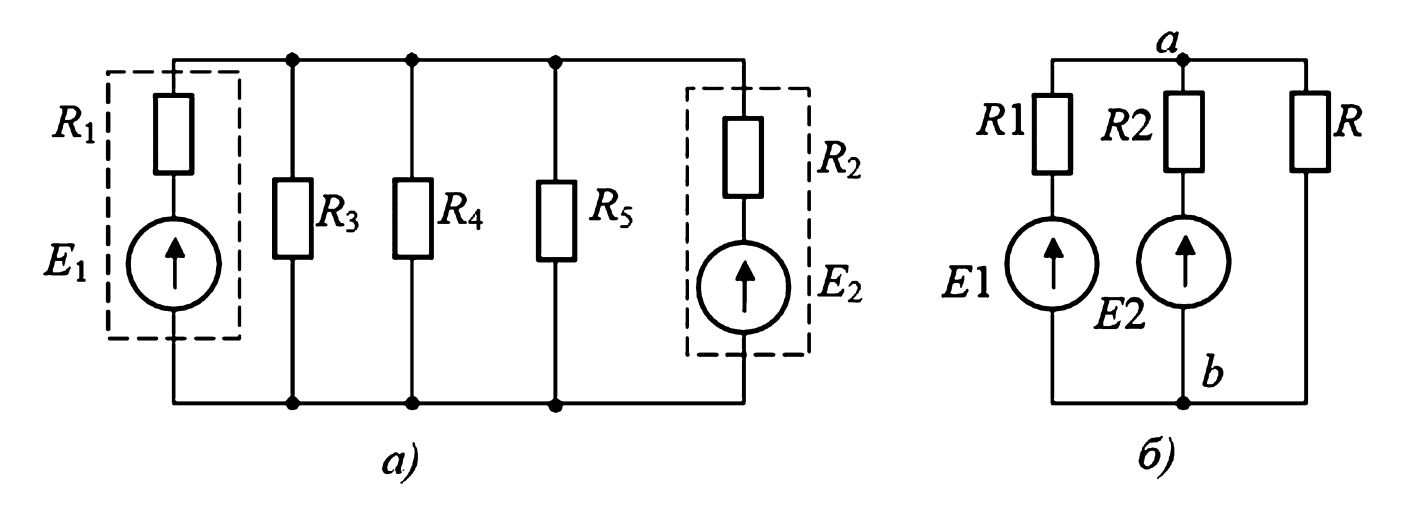
Рисунок 2. Схема электрооборудования: а — исходная; б — расчетная модель

(а — исходная схема с множеством ламп и двигателей; б — преобразованная расчетная схема, где все потребители заменены одним резистором R. Источники E1 и E2 включены параллельно нагрузке R.)

Анализ вариантов:

Для расчетов используется та же базовая формула (1), адаптированная для данной схемы:

$$U = \frac{E_1/R_1 + E_2/R_2}{1/R_1 + 1/R_2 + 1/R}$$

Вариант	Параметры ($E_1$, $R$)	Напряжение сети $U$, В	Ток генератора $I_1$, А	Ток АКБ $I_2$, А	Вывод о режиме работы
1	$E_1=12$ В, $R=1$ Ом	12.5	-12.5	25.0	Генератор потребляет (режим двигателя), АКБ разряжается.
2	$E_1=13$ В, $R=1$ Ом	12.83	4.28	8.55	Оба источника работают в режиме генерации, питая нагрузку.
3	$E_1=14$ В, $R=1$ Ом	13.16	21.0	-7.9	Генератор питает нагрузку и заряжает АКБ (ток АКБ отрицательный).
4	$E_1=14$ В, $R=0.5$ Ом	12.99	25.3	0.65	При мощной нагрузке оба источника снова переходят в режим генерации, даже при высоком ЭДС генератора.

Инженерный вывод: Пример 2 наглядно демонстрирует «перетекание» нагрузок между параллельными источниками постоянного тока в зависимости от их внутренней ЭДС и общего сопротивления сети. Это критически важно учитывать при проектировании систем бесперебойного питания и бортовых сетей транспортных средств.

3. Сравнительный анализ методов расчета

Чтобы понять место метода двух узлов среди других инструментов инженера, сравним его с классическими методами.

Таблица 1. Сравнение методов расчета электрических цепей
Метод	Область применения	Количество уравнений	Сложность вычислений
Метод двух узлов	Цепи с двумя выраженными узлами (параллельные ветви)	1 (одно!)	Низкая
Метод узловых потенциалов (общий)	Любые сложные цепи	$N_{узлов} — 1$	Средняя
Метод контурных токов	Любые сложные цепи (особенно планарные)	$N_{ветвей} — N_{узлов} + 1$	Средняя/Высокая
Законы Кирхгофа (прямое применение)	Простые цепи, учебные задачи	$N_{ветвей}$	Высокая (громоздко)

4. Преимущества и недостатки метода

Как и любой инженерный инструмент, метод имеет свои сильные и слабые стороны.

Преимущества:

Экстремальная простота: решение всего одного уравнения вместо системы.
Минимизация ошибок: меньше вычислений — меньше вероятность арифметической ошибки.
Наглядность: физический смысл каждого слагаемого в числителе (токи короткого замыкания ветвей) и знаменателе (проводимости) понятен инженеру.

Недостатки:

Ограниченная применимость: подходит только для специфической топологии цепи (два узла).
Сложность с идеальными источниками ЭДС: если в ветви есть идеальный источник ЭДС (без сопротивления), проводимость ветви стремится к бесконечности, что требует особого подхода к предельному переходу в формуле.

5. Интересные факты о методе двух узлов

В англоязычной литературе этот метод известен как Теорема Миллмана (Millman’s theorem), названная в честь Джейкоба Миллмана, который популяризировал её в 1940-х годах.
Метод является электрическим аналогом нахождения центра масс в механике, где проводимости играют роль масс, а потенциалы — роль координат.
Он идеально подходит для расчета современных систем на базе возобновляемых источников энергии, где множество солнечных панелей или ветрогенераторов подключены к одной шине постоянного тока.
В микроэлектронике этот метод используется для быстрого расчета потенциала общей подложки чипа при наличии множества токов утечки.
Если в цепи есть только источники тока, формула упрощается до закона Ома для участка цепи: $U = I_{\sum} \cdot R_{\text{экв}}$.
Метод работает и для цепей переменного тока, если проводить вычисления в комплексных числах (используя комплексные проводимости и фазоры ЭДС).
Многие современные симуляторы схем (SPICE, Multisim) используют модифицированный метод узловых потенциалов как основной алгоритм движка, частью которого является логика метода двух узлов.

6. FAQ: Часто задаваемые вопросы

Вопрос 1: Что делать, если в цепи больше двух узлов, но они соединены «звездой» или «треугольником»?

В таком случае необходимо сначала применить преобразование «звезда-треугольник» для упрощения схемы, либо использовать общий метод узловых потенциалов.

Вопрос 2: Можно ли применять этот метод для цепей переменного тока?

Да, метод полностью применим для цепей синусоидального тока. В этом случае все величины (ЭДС, токи, проводимости) должны быть представлены в комплексной форме.

Вопрос 3: Как учитывать ветвь с идеальным вольтметром?

Идеальный вольтметр имеет бесконечное сопротивление ($R \to \infty$, $g \to 0$). Такая ветвь просто не учитывается в сумме проводимостей в знаменателе формулы (1).

Вопрос 4: Что произойдет, если одна из ветвей содержит идеальный источник ЭДС (R=0)?

В этом случае метод в классическом виде применять нельзя, так как $g \to \infty$. Однако, это означает, что напряжение между узлами просто равно ЭДС этого идеального источника.

Вопрос 5: Влияет ли выбор заземленного узла на результат?

Нет, выбор опорного узла влияет только на абсолютные значения потенциалов, но разность потенциалов (напряжение $U_{12}$) и токи в ветвях останутся неизменными.

Вопрос 6: Нужно ли учитывать внутреннее сопротивление источников при расчете?

Обязательно. Внутреннее сопротивление источника $R_{вн}$ суммируется с сопротивлением нагрузки в его ветви для получения корректного значения проводимости $g_k = 1/(R_{нагр} + R_{вн})$.

Вопрос 7: Какой знак ставить перед током источника тока J в формуле?

Если стрелка источника тока направлена к узлу, потенциал которого мы определяем (не заземленному), ставится «плюс». Если от узла — «минус».

Заключение

Метод двух узлов остается одним из самых элегантных и мощных инструментов в арсенале инженера-электрика. Несмотря на развитие компьютерного моделирования, понимание этого метода необходимо для быстрой экспресс-оценки режимов работы оборудования, проверки результатов машинного расчета и глубокого понимания физических процессов перераспределения токов в параллельных ветвях.

Нормативная база и литература

ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий. — Введ. 2004-01-01. — М.: Изд-во стандартов, 2003.
ГОСТ 2.702-2011. Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем. — М.: Стандартинформ, 2012.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2016.
Millman, J. (1940). A Useful Network Theorem. Proceedings of the IRE, 28(9), 413-417.