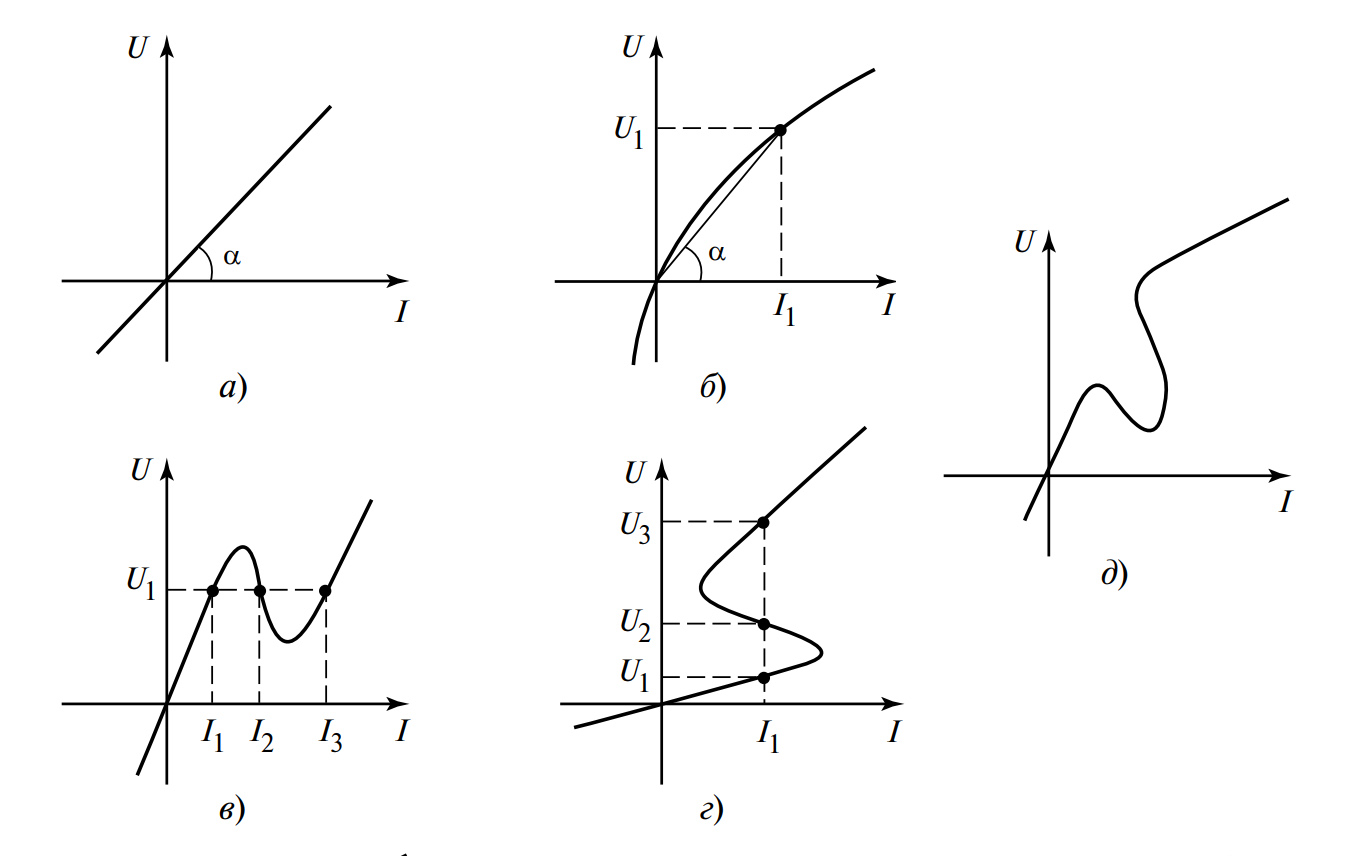Линейные и нелинейные электрические цепи

Содержание страницы

1. Линейные и нелинейные элементы
2. Анализ вольт-амперных характеристик (ВАХ)
3. Преимущества и недостатки линейного и нелинейного подходов
4. Интересные факты по теме
5. Часто задаваемые вопросы (FAQ)
Заключение

Линейная электрическая цепь — это фундаментальная модель в электротехнике, представляющая собой совокупность электрических устройств, параметры которых (сопротивление, индуктивность, емкость) остаются постоянными и не зависят от величин протекающих токов и приложенных напряжений. Ключевым свойством таких цепей является подчинение принципу суперпозиции (наложения).

Нелинейная электрическая цепь — это цепь, в состав которой входит хотя бы один нелинейный элемент, то есть элемент, чьи параметры изменяются в зависимости от тока или напряжения. Такие цепи не подчиняются принципу суперпозиции, что кардинально усложняет их анализ.

Исторически теория электрических цепей началась с линейных моделей. Работы Георга Ома (1827 г.) и Густава Кирхгофа (1845 г.) заложили фундамент для анализа цепей постоянного тока. Однако с изобретением вакуумных ламп, а позднее — полупроводниковых приборов (диодов, транзисторов), стало очевидно, что большинство реальных устройств ведут себя нелинейно. Это потребовало разработки новых, более сложных методов анализа, но именно нелинейные элементы лежат в основе всей современной электроники, обеспечивая возможность усиления, генерирования и преобразования сигналов.

Примечание: Основное различие между линейными и нелинейными цепями заключается в применимости принципа суперпозиции. В линейной цепи реакция на сумму воздействий равна сумме реакций на каждое воздействие по отдельности. В нелинейной цепи это правило не выполняется.

1. Линейные и нелинейные элементы

Линейный элемент электрической цепи постоянного тока (будь то источник напряжения, источник тока или резистивный элемент) — это такой элемент, у которого ток и напряжение связаны строгими линейными зависимостями. Элемент, не удовлетворяющий этому условию, называется нелинейным.

Зависимости напряжения от тока у источников (ЭДС и тока) называют внешними характеристиками, а у резистивных элементов — вольт-амперными характеристиками (ВАХ). Как следует из данных определений, у линейных элементов эти зависимости должны быть линейными (графически — прямыми линиями), у нелинейных элементов — нелинейными (графически — кривыми линиями).

В данном материале мы сосредоточимся на вольт-амперных характеристиках (ВАХ) резистивных элементов.

Таблица 1. Графические обозначения резистивных элементов

Условные графические обозначения (УГО) элементов в электрических схемах стандартизированы. В Российской Федерации эти обозначения регламентируются Единой системой конструкторской документации (ЕСКД), в частности, действующим стандартом ГОСТ 2.728-74 «ЕСКД. Обозначения условные графические в схемах. Резисторы, конденсаторы».

Наименование резистора	Условное обозначение (согласно ГОСТ 2.728-74)
Резистор постоянный (линейный)
Резистор нелинейный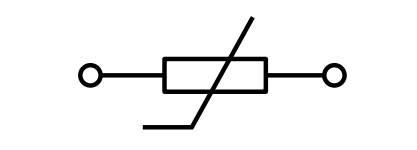
Резистор переменный (реостат)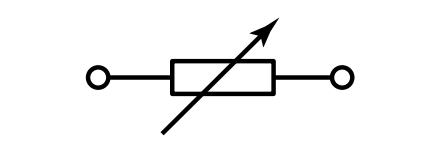
Резистор подстроечный с разрывом цепи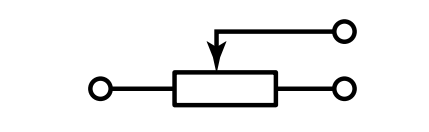
Резистор подстроечный без разрыва цепи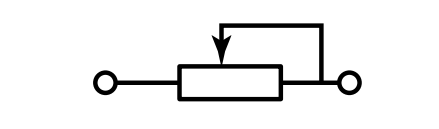

2. Анализ вольт-амперных характеристик (ВАХ)

Вольт-амперные характеристики могут быть построены экспериментально, при этом каждая их точка дает значение постоянного напряжения резистора при данном значении его постоянного тока и совпадении их условно-положительных направлений. Такие ВАХ называют статическими в отличие от динамических ВАХ, снятых при достаточно быстрых изменениях тока.

Это отличие обусловлено в основном зависимостью сопротивления (проводимости) от температуры (как, например, в лампах накаливания) или иными инерционными процессами. В рамках данного обзора мы будем рассматривать только статические ВАХ.

2.1. Статическое и дифференциальное сопротивление

Если каждую точку графика ВАХ (с координатами $U_1$, $I_1$) соединить с началом координат (рис. 1, а, б), то тангенс угла наклона $\alpha$ такой соединительной линии (секущей) к оси абсцисс (оси напряжений) дает величину, обратную статическому сопротивлению.

Более строго, статическое сопротивление $R$ в любой точке ВАХ равно отношению напряжения к току в этой точке:

$$ R = \frac{U_1}{I_1} = \text{ctg}(\alpha) $$

При построении графиков ВАХ часто по оси ординат откладывают ток $I$, а по оси абсцисс — напряжение $U$. В этом случае:

$$ R = R(U, I) = \frac{U}{I} = k \cdot \text{ctg}(\alpha) $$

где $k = m_U/m_I$; $m_U$ и $m_I$ — масштабные коэффициенты для осей напряжения и тока.

Для нелинейных элементов также вводят понятие дифференциального сопротивления $R_{\text{diff}}$, которое характеризует поведение элемента для малых изменений тока и напряжения в окрестности рабочей точки. Оно определяется как производная напряжения по току в данной точке ВАХ:

$$ R_{\text{diff}} = \frac{dU}{dI} $$

Дифференциальное сопротивление равно тангенсу угла наклона касательной к ВАХ в рабочей точке (если ось $I$ — ордината, а $U$ — абсцисса).

2.2. ВАХ линейного элемента

График ВАХ линейного резистивного элемента представляет собой прямую линию, проходящую через начало координат (рис. 1, а). Сопротивление такого элемента неизменно и является константой:

$$ R = R(U, I) = \frac{U}{I} = \text{const} $$

У линейного элемента статическое сопротивление $R$ и дифференциальное сопротивление $R_{\text{diff}}$ равны и постоянны в любой точке.

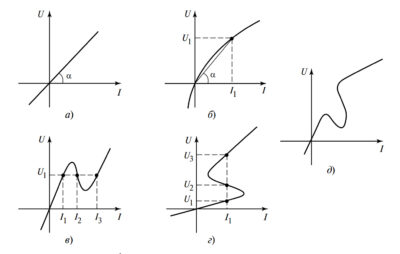
Рисунок 1. Вольт-амперные характеристики:
а — линейная ВАХ;
б — нелинейная возрастающая ВАХ;
в — ВАХ, управляемая током;
г — ВАХ, управляемая напряжением;
д — неуправляемая ВАХ.

2.3. Типы ВАХ нелинейных элементов

График ВАХ нелинейного резистивного элемента — кривая линия. Выделяют четыре основных типа ВАХ нелинейных элементов.

ВАХ является возрастающей функцией (рис. 1, б). Каждая точка ее графика однозначно определяет как ток, так и напряжение. То есть, любому значению тока $I$ соответствует одно значение напряжения $U$, и наоборот. Примером могут служить терморезисторы или варисторы.
ВАХ, управляемая током (рис. 1, в). Характеристика является такой функцией, каждому значению тока которой отвечает одно значение напряжения, но некоторым значениям напряжения могут отвечать сразу несколько (например, три) значений тока. Такие ВАХ и соответствующие им сопротивления называют управляемыми током, так как ток однозначно задает состояние элемента. Их описывают функциями вида: $U = f(I)$, $R = R(I)$. Пример элемента — туннельный диод.
ВАХ, управляемая напряжением (рис. 1, г). Характеристика является такой функцией, каждому значению напряжения которой отвечает одно значение тока, но некоторым значениям тока могут отвечать сразу несколько значений напряжения. Такие ВАХ и соответствующие им сопротивления называют управляемыми напряжением, так как напряжение однозначно задает состояние. Их описывают функциями вида: $I = \phi(U)$, $R = R(U)$. Пример элемента — газоразрядная лампа, тиристор.
ВАХ неуправляемая (рис. 1, д). Является многозначной функцией как по току, так и по напряжению. Такая ВАХ называется неуправляемой. Подобные характеристики могут описывать элементы с гистерезисом, где состояние зависит от предыстории (например, магнитные цепи).

Знакомство с ВАХ линейных и нелинейных элементов свидетельствует о значительной простоте первых и многообразии и сложности вторых. Поэтому выделение класса линейных электрических цепей, исследование которых представляется намного более простой задачей, чем исследования нелинейных цепей, исключительно важно.

Вместе с тем надо понимать, что линейность электрической цепи на практике возможна лишь для определенного диапазона изменения токов и напряжений, вне которого цепь становится нелинейной (например, любой резистор сгорит при превышении допустимого тока, что является крайне нелинейным эффектом).

3. Преимущества и недостатки линейного и нелинейного подходов

Таблица 2. Сравнение линейных и нелинейных цепей

Параметр	Линейные цепи	Нелинейные цепи
Основные элементы	Идеальные резисторы (R), катушки (L), конденсаторы (C) с постоянными параметрами.	Диоды, транзисторы, тиристоры, лампы, варисторы, терморезисторы.
Форма ВАХ	Прямая линия, проходящая через начало координат.	Кривая линия (S-образная, N-образная, возрастающая и т.д.).
Основной закон	Закон Ома ($U = I \cdot R$, где $R = \text{const}$).	Сложные нелинейные зависимости ($I = f(U)$ или $U = f(I)$).
Принцип суперпозиции	Применим. Анализ сложных цепей упрощается.	Неприменим.
Методы анализа	Алгебраические (законы Кирхгофа), метод контурных токов, узловых потенциалов, эквивалентного генератора.	Графический, аналитический (кусочно-линейная аппроксимация), численные методы.
Функциональность	Фильтрация, деление напряжения/тока, согласование.	Выпрямление, усиление, генерация, переключение, модуляция.
Сложность анализа	Низкая или средняя.	Высокая.

4. Интересные факты по теме

Лампа накаливания — нелинейна: Обычная лампа накаливания является классическим примером нелинейного резистивного элемента. Ее сопротивление в холодном состоянии в 10-15 раз ниже, чем в рабочем (нагретом), из-за чего ее ВАХ — ярко выраженная кривая.
Линейность — это идеализация: В реальности абсолютно линейных элементов не существует. Любой пассивный элемент (даже прецизионный резистор) имеет нелинейные свойства, которые проявляются при высоких напряжениях, частотах или изменении температуры. Однако в заданных рабочих диапазонах их нелинейностью можно пренебречь.
Основа всей цифровой техники: Вся современная цифровая логика (процессоры, память) построена на транзисторах, работающих в ключевом (крайне нелинейном) режиме «включено/выключено».
Хаос в цепях: Некоторые нелинейные RLC-цепи (например, «схема Чуа») могут демонстрировать хаотическое поведение. Их состояние непредсказуемо в долгосрочной перспективе, несмотря на то, что они описываются детерминированными уравнениями.
Появление нелинейности: Когда синусоидальный сигнал проходит через нелинейную цепь, на выходе появляются новые частоты (гармоники), которых не было во входном сигнале. На этом свойстве основана работа умножителей частоты и смесителей.

5. Часто задаваемые вопросы (FAQ)

1. Что такое принцип суперпозиции и почему он так важен?

Принцип суперпозиции гласит, что в линейной цепи с несколькими источниками ток в любой ветви равен алгебраической сумме токов, создаваемых каждым источником в отдельности (при этом остальные источники «выключаются» — источники ЭДС заменяются коротким замыканием, источники тока — разрывом). Это позволяет свести сложную задачу к нескольким простым. В нелинейных цепях этот принцип не работает, и их приходится рассчитывать «целиком».

2. В чем разница между статическим и дифференциальным сопротивлением?

Статическое сопротивление ($R = U/I$) — это «обычное» сопротивление в рабочей точке, оно определяет мощность, рассеиваемую элементом ($P = U \cdot I = I^2 R$). Дифференциальное сопротивление ($R_{\text{diff}} = dU/dI$) — это сопротивление элемента для малого переменного сигнала, наложенного на постоянный ток. Именно $R_{\text{diff}}$ используется при расчете усилительных каскадов на транзисторах. У нелинейных элементов эти два значения не совпадают.

3. Почему диод называют нелинейным элементом?

ВАХ идеального диода состоит из двух прямых: при прямом смещении (U > 0) сопротивление равно нулю (ток бесконечен), при обратном (U < 0) — сопротивление бесконечно (ток равен нулю). ВАХ реального диода — это крутая экспоненциальная кривая. В обоих случаях это не прямая линия, проходящая через ноль под одним углом, поэтому диод является нелинейным элементом. Его основное свойство — выпрямление — прямое следствие этой нелинейности.

4. Что такое кусочно-линейная аппроксимация?

Это один из самых распространенных аналитических методов расчета нелинейных цепей. Сложная кривая ВАХ нелинейного элемента (например, диода) заменяется набором прямых отрезков (кусочков). Например, ВАХ диода аппроксимируют двумя отрезками: при U < U_th (пороговое напряжение) сопротивление бесконечно, при U > U_th сопротивление — некое малое постоянное значение $R_f$. Это позволяет применить к каждому «кусочку» методы анализа линейных цепей.

5. Являются ли катушка индуктивности и конденсатор линейными элементами?

В теории цепей — да. Их зависимости линейны: для катушки напряжение пропорционально *производной* тока ($U = L \cdot dI/dt$), для конденсатора ток пропорционален *производной* напряжения ($I = C \cdot dU/dt$). Так как $L$ и $C$ считаются константами, эти элементы линейны. Однако в реальности, например, катушка с ферромагнитным сердечником является нелинейной, так как ее индуктивность $L$ сильно зависит от тока (эффект насыщения сердечника).

Заключение

Разделение электрических цепей на линейные и нелинейные является фундаментальным в электротехнике. Линейные цепи, подчиняющиеся закону Ома и принципу суперпозиции, служат основой для понимания базовых процессов и легко поддаются математическому анализу.

Нелинейные цепи, хотя и значительно сложнее в расчетах, являются основой всей современной электроники, позволяя реализовывать функции усиления, выпрямления, генерации и цифровой логики. Ключом к пониманию любого элемента, как линейного, так и нелинейного, является его вольт-амперная характеристика (ВАХ), которая графически представляет закон, связывающий ток и напряжение в данном устройстве.

Нормативная база

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Стандарт устанавливает основные термины, используемые в области электротехники, включая определения для электрических цепей и их элементов.
ГОСТ 2.728-74 «Единая система конструкторской документации. Обозначения условные графические в схемах. Резисторы, конденсаторы» (Действующий). Определяет стандартные графические обозначения для резисторов (включая нелинейные) и конденсаторов на электрических схемах.

Линейные и нелинейные электрические цепи: определения, ВАХ, классификация