Круговые и линейные диаграммы в трехфазных цепях

Содержание страницы

Анализ схемы с переменным сопротивлением в одной фазе
Анализ различных типов сопротивления $Z_A$
Таблица анализа режимов
Преимущества и недостатки метода
Интересные факты
FAQ: Часто задаваемые вопросы
Заключение

Круговые и линейные диаграммы в трехфазных цепях — это графический метод анализа (также известный как годограф или геометрическое место точек), который наглядно демонстрирует, как изменяются комплексные величины (векторы) фазных напряжений и токов при плавном изменении параметра одного из элементов цепи. Этот метод является прямым развитием векторных диаграмм и широко использует теорему об эквивалентном генераторе.

Исторически этот подход получил широкое распространение в электротехнике для анализа режимов работы электрических машин, в частности, асинхронных двигателей (где он известен как диаграмма Гей-Горгеса). В данном материале мы рассмотрим применение этого метода для анализа несимметричных режимов в стационарной трехфазной цепи.

Основной принцип: Если в электрической цепи изменяется модуль комплексного сопротивления одной из ветвей, а его аргумент (фазовый угол) остается постоянным, то геометрическим местом концов векторов напряжений и токов в любой части цепи является дуга окружности. В частном случае, если аргумент равен нулю (активное сопротивление), диаграмма вырождается в прямую линию.

Анализ схемы с переменным сопротивлением в одной фазе

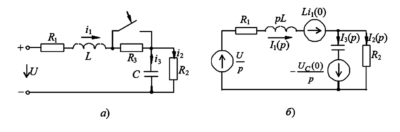
Рассмотрим классический пример, иллюстрирующий построение круговой диаграммы. Возьмем трехфазную цепь, соединенную по схеме «звезда-звезда» без нейтрального провода (рис. 1а). В фазах B и C установлены одинаковые постоянные активные сопротивления (резисторы): $Z_B = Z_C = R = \text{const}$. В фазе A включено переменное сопротивление $Z_A$, модуль которого может изменяться от 0 до $\infty$, но его характер (емкостный, индуктивный или активный) остается неизменным.

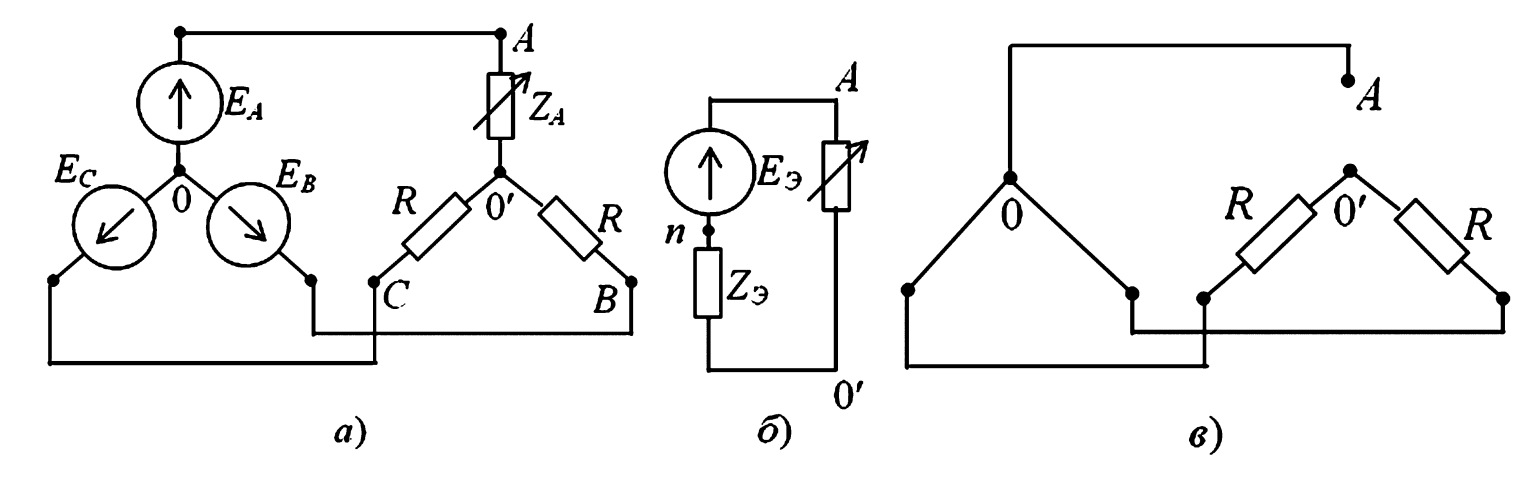
Рис. 1. Схема цепи при изменении сопротивления в фазе А:

а — исходная схема;
б — эквивалентная схема по методу эквивалентного генератора;
в — схема для определения эквивалентного сопротивления.

Применение метода эквивалентного генератора

Для анализа этой схемы и нахождения зависимости напряжений от $Z_A$, наиболее удобно применить метод эквивалентного генератора (теорему Тэвенена). Мысленно отключаем изменяющийся элемент $Z_A$ от узлов A и n (нейтраль нагрузки) и заменяем всю оставшуюся часть схемы (трехфазный источник и сопротивления $Z_B$, $Z_C$) одним эквивалентным генератором, подключенным к тем же узлам (рис. 1б).

Параметры этого эквивалентного генератора определяются следующим образом:

ЭДС эквивалентного генератора ($E_Э$): Равна напряжению холостого хода между точками A и n, когда $Z_A$ отключена. В этом режиме $Z_B$ и $Z_C$ (обе равны $R$) оказываются соединены последовательно с суммарным напряжением $U_{BC}$. Для симметричной системы источников ЭДС напряжение смещения нейтрали $U_{nO’}$ равно $-U_A / 2$. Тогда напряжение холостого хода $E_Э$ (напряжение между точкой A и точкой n) будет:
$$E_Э = U_{An, \text{хх}} = U_A — U_n = U_A — (-U_A / 2) = 1.5 \cdot U_A$$
(Или $E_Э = 1.5 \cdot U_Ф$, где $U_Ф$ — фазное напряжение источника).
Внутреннее сопротивление ($Z_Э$): Равно входному сопротивлению пассивной схемы со стороны зажимов A и n при закороченных источниках ЭДС (рис. 1в). При этом точки A, B, C замыкаются на нейтраль источника O’. Относительно узла n, сопротивления $Z_B$ и $Z_C$ оказываются включенными параллельно между точкой n и общей точкой O’ (к которой теперь подключена и точка A). Таким образом, эквивалентное сопротивление равно:
$$Z_Э = \frac{Z_B \cdot Z_C}{Z_B + Z_C} = \frac{R \cdot R}{R + R} = \frac{R}{2}$$

Теперь эквивалентная схема (рис. 1б) представляет собой простой контур из $E_Э$, $Z_Э$ и подключенной к ним нагрузки $Z_A$. Годограф тока $I_A = E_Э / (Z_Э + Z_A)$ или напряжения на фазе $U_{An} = I_A \cdot Z_A$ будет представлять собой окружность.

Анализ различных типов сопротивления $Z_A$

Вид диаграммы (окружность или прямая) и ее расположение зависят от разности фазовых углов сопротивлений $Z_A$ и $Z_Э$. Обозначим эту разность $\psi = \phi_A — \phi_Э$. В нашем случае сопротивление $Z_Э = R/2$ является чисто активным, поэтому его фазовый угол $\phi_Э = 0$. Следовательно, $\psi = \phi_A$.

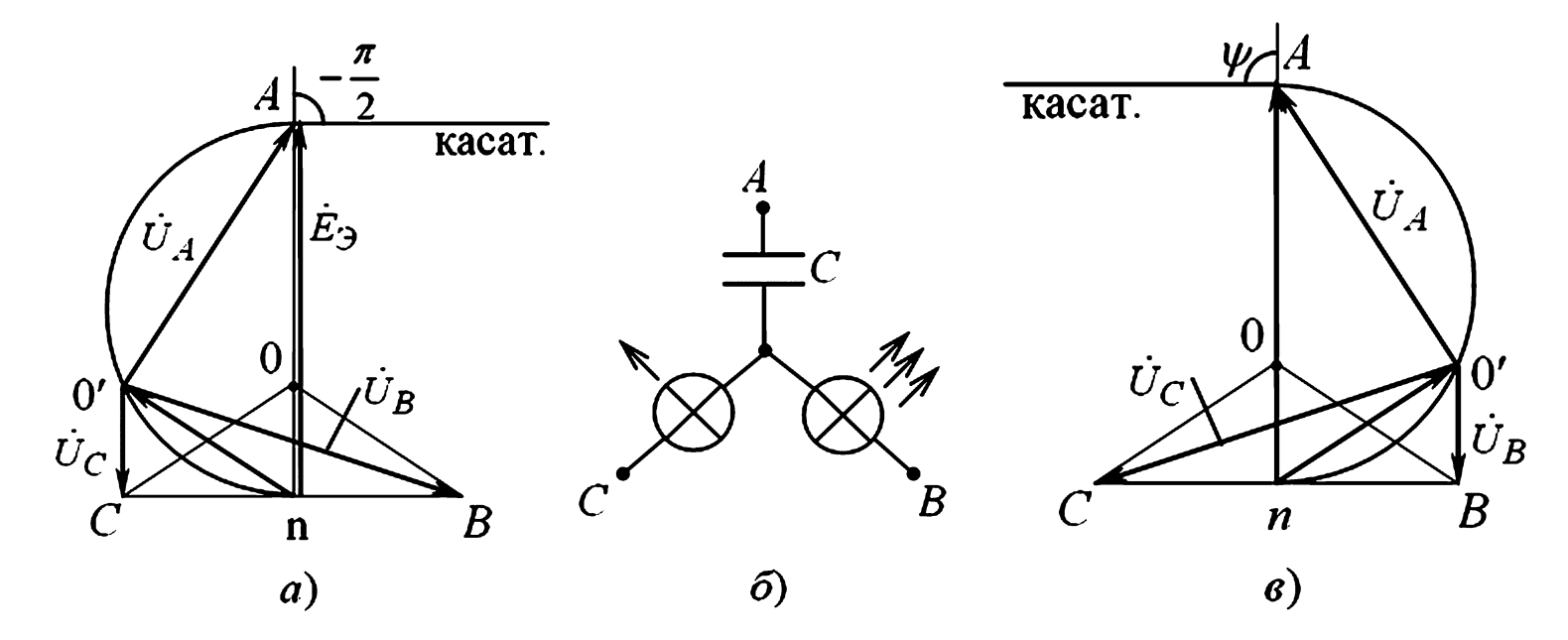
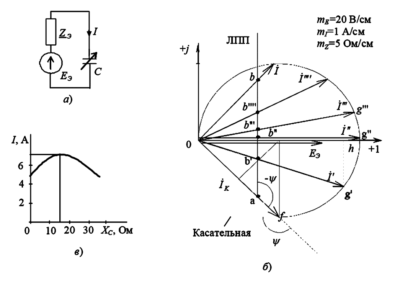
Рис. 2. Круговые диаграммы при изменении сопротивления в фазе А:

а — емкостного;
б — схема фазоуказателя;
в — индуктивного.

1. $Z_A$ — переменное емкостное сопротивление ($Z_A = -jX_C$)

Если в фазе A изменяется емкостное сопротивление (например, путем изменения емкости конденсатора), то его фазовый угол $\phi_A = -\pi/2$.

Угол $\psi$: $\psi = \phi_A — \phi_Э = -\pi/2 — 0 = -\pi/2$.
Вид диаграммы: Годограф конца вектора напряжения смещения нейтрали $U_{nO’}$ (или фазного напряжения $U_{An}$) представляет собой дугу окружности (показано на рис. 2а).
Свойства: В этом режиме возникает несимметрия фазных напряжений нагрузки. Анализ векторной диаграммы (рис. 2а) показывает, что при любом значении $X_C$ (от 0 до $\infty$) **напряжение на фазе B ($U_{Bn}$) всегда оказывается больше, чем на фазе C ($U_{Cn}$)**.
Применение: Этот эффект лежит в основе работы простейших фазоуказателей (рис. 2б). Прибор состоит из двух одинаковых ламп накаливания (активные сопротивления, как $Z_B$ и $Z_C$) и конденсатора (емкостное сопротивление, как $Z_A$). При подключении к сети по схеме «звезда-звезда» без нейтрали, лампа, которая горит ярче (на ней большее напряжение), указывает на фазу, следующую за фазой, к которой подключен конденсатор. Это критически важно для определения порядка чередования фаз при подключении генераторов, трансформаторов и трехфазных двигателей.

2. $Z_A$ — переменное индуктивное сопротивление ($Z_A = jX_L$)

Если в фазе A изменяется индуктивное сопротивление (например, катушка с переменной индуктивностью), то его фазовый угол $\phi_A = +\pi/2$.

Угол $\psi$: $\psi = \phi_A — \phi_Э = +\pi/2 — 0 = +\pi/2$.
Вид диаграммы: Годограф также представляет собой дугу окружности (показано на рис. 2в).
Свойства: В этом случае наблюдается обратный эффект по сравнению с емкостной нагрузкой. **Напряжение на фазе C ($U_{Cn}$) всегда будет больше напряжения на фазе B ($U_{Bn}$)**.

3. $Z_A$ — переменное активное сопротивление ($Z_A = R_A$)

Это особый случай, когда в фазе A изменяется чисто активное сопротивление (например, реостат). Фазовый угол $\phi_A = 0$.

Угол $\psi$: $\psi = \phi_A — \phi_Э = 0 — 0 = 0$.
Вид диаграммы: Когда фазовые углы эквивалентного генератора и переменной нагрузки совпадают, круговая диаграмма вырождается в прямую линию (линейную диаграмму).
Свойства: Нейтраль нагрузки ‘n’ перемещается по отрезку прямой. При этом напряжения на «здоровых» фазах B и C ($U_{Bn}$ и $U_{Cn}$) будут равными между собой при любом значении $R_A$. Напряжение на самой фазе A ($U_{An}$) будет изменяться также по прямой линии в диапазоне от $0$ (при $R_A = 0$, т.е. коротком замыкании фазы) до $1.5 \cdot U_Ф$ (при $R_A = \infty$, т.е. обрыве фазы).

Таблица анализа режимов

Характеристика	Емкостное сопротивление ($Z_A = -jX_C$)	Индуктивное сопротивление ($Z_A = jX_L$)	Активное сопротивление ($Z_A = R_A$)
Фазовый угол $\phi_A$	$-\pi/2$ (–90°)	$+\pi/2$ (+90°)	$0$
Разность углов $\psi = \phi_A — \phi_Э$	$-\pi/2$	$+\pi/2$	$0$
Вид диаграммы (годографа)	Круговая	Круговая	Линейная (прямая)
Соотношение напряжений	$U_{Bn} > U_{Cn}$	$U_{Cn} > U_{Bn}$	$U_{Bn} = U_{Cn}$
Практическое применение	Фазоуказатели	Анализ несимметрии	Анализ обрыва/КЗ фазы

Преимущества и недостатки метода

Преимущества

Наглядность: Метод позволяет визуализировать, как изменение одного параметра влияет на всю цепь, что сложно воспринять из сухих формул.
Качественный анализ: Позволяет быстро оценить предельные режимы (КЗ и холостой ход) и характер несимметрии.
Практическая основа: На этом принципе основаны реальные измерительные приборы (фазоуказатели) и методы анализа (диаграмма асинхронного двигателя).

Недостатки

Ограниченная точность: Графическое построение всегда уступает в точности аналитическим расчетам.
Сложность: При одновременном изменении нескольких параметров или в более сложных схемах построение диаграмм становится чрезвычайно громоздким.
Узкая применимость: Метод наиболее эффективен, когда меняется только один параметр, а остальные постоянны.

Интересные факты

Годограф вектора напряжения или тока при изменении одного комплексного сопротивления является частным случаем дробно-линейного преобразования (или преобразования Мёбиуса) вида $w = (az+b)/(cz+d)$, которое всегда отображает окружности и прямые в окружности и прямые.
Самой известной круговой диаграммой в электротехнике является диаграмма Гей-Горгеса (или Оссанны), которая описывает режимы работы асинхронного двигателя.
Точка, соответствующая режиму холостого хода ($Z_A = \infty$) и точка короткого замыкания ($Z_A = 0$) являются фундаментальными точками для построения любой круговой диаграммы.
Фазоуказатель с двумя лампами и конденсатором не будет работать в однофазной сети, так как для его работы необходимо наличие вращающегося в определенном порядке магнитного поля (или системы векторов ЭДС).
Если в рассмотренной схеме сопротивление $Z_A$ станет равным $R$, то есть $Z_A = Z_B = Z_C = R$, система станет симметричной, напряжение смещения нейтрали $U_{nO’}$ станет равно нулю, а фазные напряжения нагрузки будут равны фазным напряжениям источника.
Анализ несимметричных режимов можно также проводить методом симметричных составляющих, который является более универсальным, но менее наглядным.
При обрыве фазы A ($R_A = \infty$) в рассмотренной схеме, напряжение на этой фазе ($U_{An}$) становится равно $1.5 \cdot U_Ф$, а не нулю, что часто является неожиданностью для начинающих.

FAQ: Часто задаваемые вопросы

1. Что такое «годограф вектора»?

Годограф вектора — это линия (кривая), которую описывает конец вектора на комплексной плоскости, если один из параметров, определяющих этот вектор (например, сопротивление), плавно изменяется.

2. Почему диаграмма для активного сопротивления $R_A$ становится линейной?

Диаграмма становится линейной, потому что фазовый угол переменного сопротивления $Z_A = R_A$ (равный 0) совпадает с фазовым углом эквивалентного сопротивления $Z_Э = R/2$ (также равным 0). Их разность $\psi = 0$. В этом частном случае окружность «вырождается» в прямую линию.

3. Что означает $U_Ф$ в формулах?

$U_Ф$ — это обозначение фазного напряжения источника питания, то есть напряжения между одним из фазных проводов (A, B или C) и нейтралью источника (O’).

4. Насколько важно соблюдать порядок чередования фаз?

Критически важно. Если неправильно подключить трехфазный асинхронный двигатель, его ротор будет вращаться в обратную сторону. При параллельном включении генераторов или трансформаторов несовпадение порядка чередования фаз приведет к межфазному короткому замыканию.

5. Что произойдет, если $Z_B$ и $Z_C$ не будут равны друг другу?

Схема изначально станет несимметричной. Это усложнит расчеты: эквивалентное сопротивление $Z_Э$ станет комплексным (будет иметь и активную, и реактивную часть), а начальная точка $E_Э$ также сместится. Диаграмма останется круговой, но ее построение будет значительно сложнее.

6. Можно ли использовать этот метод для токов?

Да, абсолютно. В нашей эквивалентной схеме ток $I_A = E_Э / (Z_Э + Z_A)$. При изменении $Z_A$ годограф тока $I_A$ также будет представлять собой окружность (или прямую), так как это также дробно-линейное преобразование.

7. Что такое «напряжение смещения нейтрали»?

Это напряжение между нейтралью нагрузки (точкой ‘n’, где сходятся $Z_A, Z_B, Z_C$) и нейтралью источника (точкой ‘O'»). В симметричном режиме оно равно нулю. В несимметричных режимах (как в нашем примере) оно отлично от нуля, что и вызывает перекос фазных напряжений на нагрузке.

Заключение

Круговые и линейные диаграммы являются мощным аналитическим инструментом в теоретических основах электротехники. Они позволяют не просто рассчитать, а визуализировать и глубоко понять поведение сложной трехфазной цепи при изменении одного из ее параметров.

На примере простой схемы «звезда-звезда» мы увидели, как изменение характера сопротивления в одной фазе (с емкостного на индуктивное) кардинально меняет соотношение напряжений в других фазах, что имеет прямое практическое применение в фазоуказателях. Понимание этого графического метода является ключевым для студентов и инженеров, занимающихся анализом несимметричных режимов и проектированием электротехнических устройств.

Нормативная база

При анализе трехфазных цепей, особенно в контексте несимметрии и качества электроэнергии, используются следующие стандарты:

ГОСТ 32144-2013 — «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения.»
ГОСТ 30804.4.30-2013 — «Электрическая энергия. Совместимость технических средств электромагнитная. Методы измерений показателей качества электрической энергии.»
ГОСТ 11677-85 — «Трансформаторы силовые. Общие технические условия.»
ГОСТ 23875-88 — «Качество электрической энергии. Термины и определения.»

Характеристика	Емкостное сопротивление (\(Z_A = -jX_C\))	Индуктивное сопротивление (\(Z_A = jX_L\))	Активное сопротивление (\(Z_A = R_A\))
Фазовый угол \(\phi_A\)	\(-\pi/2\) (–90°)	\(+\pi/2\) (+90°)	\(0\)
Разность углов \(\psi = \phi_A — \phi_Э\)	\(-\pi/2\)	\(+\pi/2\)	\(0\)
Вид диаграммы (годографа)	Круговая	Круговая	Линейная (прямая)
Соотношение напряжений	\(U_{Bn} > U_{Cn}\)	\(U_{Cn} > U_{Bn}\)	\(U_{Bn} = U_{Cn}\)
Практическое применение	Фазоуказатели	Анализ несимметрии	Анализ обрыва/КЗ фазы

Круговые и линейные диаграммы в трехфазных цепях

Анализ схемы с переменным сопротивлением в одной фазе

Применение метода эквивалентного генератора

Анализ различных типов сопротивления \(Z_A\)

1. \(Z_A\) — переменное емкостное сопротивление (\(Z_A = -jX_C\))

2. \(Z_A\) — переменное индуктивное сопротивление (\(Z_A = jX_L\))

3. \(Z_A\) — переменное активное сопротивление (\(Z_A = R_A\))