Конденсаторы в силовой электронике: характеристики, расчет

Содержание страницы

1. Физическая природа и принцип действия конденсатора
2. Классификация и материаловедение конденсаторов
3. Сравнительная характеристика типов конденсаторов
4. Основные параметры и эквивалентные схемы замещения
5. Особенности применения в силовой электронике
6. Влияние частоты и высших гармоник на работу конденсаторов
7. Импеданс электролитических конденсаторов на высоких частотах
8. Практический пример: Расчет конденсатора звена постоянного тока (DC-Link)
9. Интересные факты о конденсаторах
10. FAQ: Часто задаваемые вопросы (ЧаВо)
Заключение

Конденсатор (от лат. condensare — «уплотнять», «сгущать») — это устройство для накопления энергии электрического поля.

История этого прибора берет свое начало в 1745 году, когда голландский физик Питер ван Мушенбрук и немецкий изобретатель Эвальд Юрген фон Клейст независимо друг от друга создали «Лейденскую банку» — первый прототип современного конденсатора. С тех пор устройство прошло путь от стеклянной банки с водой до высокотехнологичных ионисторов и пленочных компонентов силовой электроники.

В данном материале мы подробно разберем физику процессов, эквивалентные схемы, влияние частоты и гармоник, а также нюансы выбора компонентов согласно современным стандартам.

1. Физическая природа и принцип действия конденсатора

В самом общем смысле, конденсатор представляет собой двухполюсник, обладающий свойством емкости, то есть способностью накапливать электрический заряд. Конструктивно электротехнический конденсатор состоит из двух или более токопроводящих обкладок (электродов), разделенных слоем диэлектрика (изолятора). Толщина этого слоя, как правило, ничтожно мала по сравнению с линейными размерами проводящих пластин.

Аналогия:
Представьте конденсатор как мембрану в трубе с водой. Пока вода (ток) давит в одну сторону, мембрана растягивается, накапливая упругую энергию (заряд). Как только давление исчезает, мембрана стремится вернуться в исходное состояние, выталкивая воду обратно. Чем больше площадь мембраны и чем она эластичнее, тем больше воды она может «накопить» при том же давлении.

Поляризация диэлектрика: Микроскопический уровень

Процессы, протекающие внутри конденсатора при подключении напряжения, определяют его характеристики. При воздействии внешнего электрического поля на диэлектрик происходит физическое явление, называемое поляризацией. В объеме материала происходит смещение связанных электрических зарядов. Это могут быть электронные оболочки атомов, ионы кристаллической решетки или полярные молекулы (диполи).

Смещение происходит строго в соответствии с вектором напряженности электрического поля. Это приводит к тому, что центры масс положительных и отрицательных зарядов в микрообъеме вещества расходятся, образуя индуцированные электрические диполи.

Анализ распределения зарядов (Описание Рис. 1)

Для глубокого понимания процессов рассмотрим физическую модель плоского конденсатора. На рис. 1 представлена упрощенная структура распределения зарядов в плоском конденсаторе при подключении к нему внешнего источника напряжения $ U $.

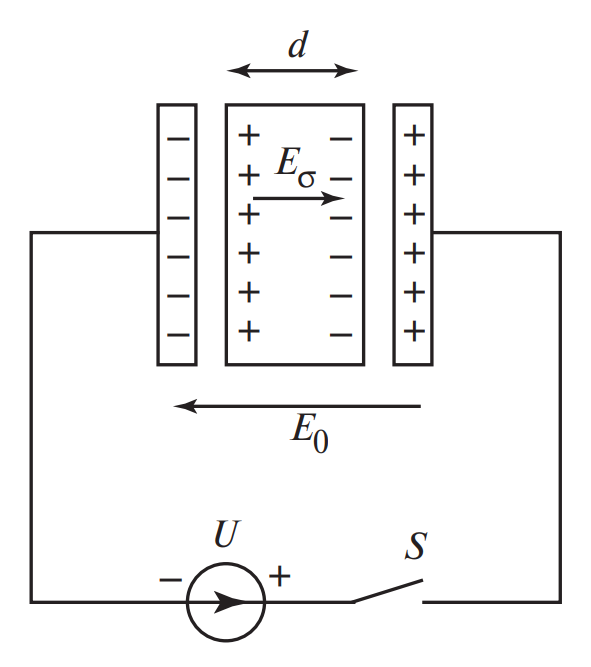
Рис. 1. Упрощенная структура распределения зарядов в плоском конденсаторе. Показано взаимодействие внешнего поля $ E_0 $ и внутреннего поля поляризации $ E_{\sigma} $.

Рассмотрим детали рисунка 1 подробнее, следуя строгой логике физического процесса:

При приложении напряжения $ U $ на проводящих обкладках накапливаются свободные заряды (обозначены знаками «+» и «–» на внешних границах).
Эти заряды создают в зазоре внешнее электрическое поле с напряженностью $ E_0 = U/d $, где $ d $ — расстояние между пластинами.
Под действием поля $ E_0 $ внутри диэлектрика происходит поляризация. На поверхности диэлектрика, обращенной к положительной обкладке, индуцируется отрицательный связанный заряд, а на противоположной — положительный.
Возникающий на поверхности диэлектрика связанный заряд создает собственное электрическое поле с напряженностью $ E_{\sigma} $.
Важнейший момент: Вектор поля $ E_{\sigma} $ направлен строго встречно внешнему полю $ E_0 $. Это приводит к частичной компенсации полей и, как следствие, к уменьшению результирующей напряженности внутри диэлектрика.

Именно этот механизм ослабления поля позволяет диэлектрику накапливать больше заряда при том же напряжении по сравнению с вакуумом. Емкость конденсатора описывается фундаментальной формулой:

C = \frac{\varepsilon_0 \varepsilon_r S}{d} \quad

Где:

$ S $ — активная площадь поверхности каждой из пластин (обкладок);
$ d $ — расстояние между пластинами (толщина диэлектрика);
$ \varepsilon_0 \approx 8.857 \times 10^{-12} $ Ф/м — электрическая постоянная вакуума;
$ \varepsilon_r $ — относительная диэлектрическая проницаемость материала ($ \varepsilon_r > 1 $).

Экспертное пояснение: Величина $ \varepsilon_r $ показывает, во сколько раз увеличивается емкость конденсатора при заполнении пространства между обкладками данным диэлектриком по сравнению с вакуумом. Для воздуха $ \varepsilon_r \approx 1 $, для полипропилена $ \approx 2.2 $, а для специальных видов керамики она может достигать $ 10^4 $ и выше.

2. Классификация и материаловедение конденсаторов

Выбор диэлектрического материала — это всегда компромисс между габаритами, стабильностью и стоимостью. Диэлектрики классифицируют по структуре молекул на:

Неполярные: Состоят из электрически нейтральных молекул (например, фторопласт, полипропилен). Отличаются малыми потерями на высоких частотах.
Полярные: Дипольные материалы, имеющие большие потери, но высокую проницаемость.
Сегнетодиэлектрики: Материалы с доменной структурой (титанат бария), обладающие гигантской $ \varepsilon_r $, но сильной зависимостью емкости от напряжения и температуры.

Особенности электролитических конденсаторов

В силовой электронике для сглаживания пульсаций напряжения в цепях постоянного тока (DC-link) незаменимы электролитические конденсаторы. Их уникальность заключается в конструкции:

Анод (+): Изготавливается из алюминиевой фольги, поверхность которой искусственно оксидируется. Слой оксида алюминия $ Al_2O_3 $ является диэлектриком.
Катод (–): Представляет собой сложную структуру, где роль второй обкладки фактически выполняет электролит (жидкий или гелеобразный), пропитывающий бумажный сепаратор, который контактирует с катодной фольгой и металлическим корпусом.

Важно! Электролитические конденсаторы являются строго полярными приборами. Ошибка в полярности подключения (соединение «плюса» источника с корпусом конденсатора) приводит к электрохимическому разрушению оксидного слоя, выделению газа, перегреву и взрыву компонента.

3. Сравнительная характеристика типов конденсаторов

Для удобства выбора приведем сравнительную таблицу основных типов конденсаторов, используемых в современной технике.

Тип диэлектрика	Диапазон емкостей	Рабочее напряжение	Тангенс угла потерь ($ \tan \delta $)	Преимущества	Недостатки
Алюминиевый электролитический	1 мкФ – 1 Ф	6.3 В – 550 В	Высокий (0.05 – 0.2)	Высокая удельная емкость, низкая цена	Малый срок службы, высыхание, плохие ВЧ свойства
Керамический (MLCC)	1 пФ – 100 мкФ	10 В – 5 кВ	Очень низкий (C0G) до среднего (X7R)	Миниатюрность, низкая индуктивность	Пьезоэффект, зависимость емкости от напряжения (DC-bias)
Пленочный (Полипропилен)	1 нФ – 100 мкФ	100 В – 3000 В	Низкий (< 0.001)	Самовосстановление, стабильность, высокие токи	Большие габариты
Танталовый	0.1 мкФ – 1000 мкФ	2.5 В – 63 В	Средний	Стабильность, высокая плотность энергии	Риск возгорания при пробое, высокая цена

4. Основные параметры и эквивалентные схемы замещения

Реальный конденсатор существенно отличается от идеальной математической модели. Основными паразитными параметрами являются:

Тангенс угла диэлектрических потерь ($ \tan \delta $): Характеризует долю энергии, рассеиваемой в тепло. При синусоидальном токе он определяется как отношение активной мощности $ P $ к реактивной $ Q $:
$$ \tan \delta = \frac{P}{Q} \quad $$
Ток утечки: Ток, протекающий через диэлектрик при постоянном напряжении (определяется сопротивлением изоляции).
ESR (Эквивалентное последовательное сопротивление): Сумма сопротивлений выводов, обкладок и потерь в диэлектрике.

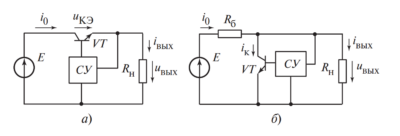
Анализ схем замещения (Описание Рис. 2)

На рис. 2 показаны упрощенные эквивалентные схемы замещения, позволяющие математически описать потери.

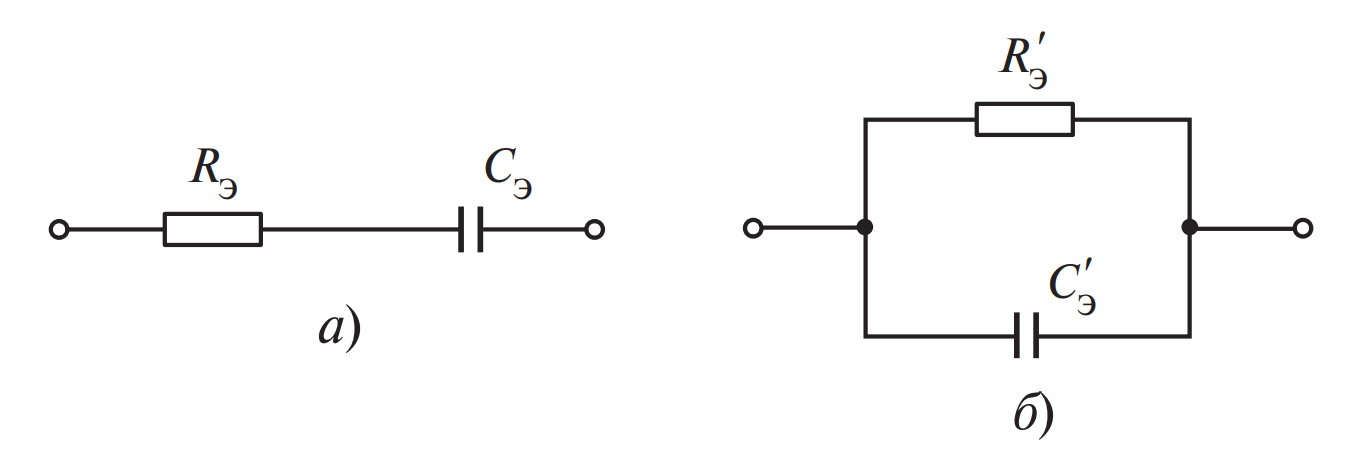
Рис. 2. Упрощенные схемы замещения конденсаторов: а — последовательная; б — параллельная.

Описание схем согласно рисунку:

Схема а (Последовательная): Конденсатор представлен идеальной емкостью $ C_э $ и последовательно включенным резистором $ R_э $. Эта схема удобна для расчетов потерь в цепях переменного тока, где ток через элемент велик. Тангенс угла потерь здесь выражается как:
$$ \tan \delta = \omega C_э R_э \quad $$
Схема б (Параллельная): Конденсатор представлен емкостью $ C’_э $ и параллельным резистором $ R’_э $. Эта модель чаще применяется для описания токов утечки диэлектрика. Формула для этой схемы:
$$ \tan \delta = \frac{1}{\omega C’_э R’_э} \quad $$

Где $ \omega = 2\pi f $ — круговая частота. Важно понимать, что параметры $ R_э $ и $ C_э $ не являются константами, а зависят от частоты и температуры.

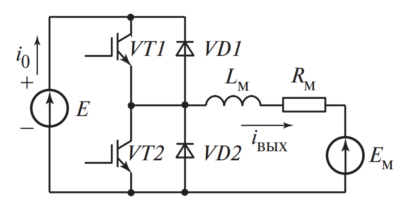
5. Особенности применения в силовой электронике

Силовая электроника предъявляет экстремальные требования к компонентам. Конденсаторы работают в условиях высоких токов, импульсных перенапряжений и значительного нагрева. Условно их можно разделить на две большие группы:

Группа 1: Неполярные конденсаторы переменного тока

Эти компоненты работают в цепях переменного напряжения или в цепях коммутации тиристоров/транзисторов. Их функции:

Компенсация реактивной мощности: Повышение $ \cos \phi $ сети.
Демпфирующие цепи (Snubbers): Формирование траектории переключения ключей, защита от перенапряжений. Здесь конденсатор принимает на себя энергию индуктивности рассеяния.
Резонансные контуры: Обеспечение мягкой коммутации (ZVS/ZCS).

Они часто подвергаются воздействию трапецеидальных импульсов тока с огромной скоростью нарастания $ di/dt $.

Группа 2: Фильтровые конденсаторы звена постоянного тока

В основном это электролитические конденсаторы большой емкости. Они служат буфером энергии между выпрямителем и инвертором. Их главная задача — обеспечить низкий импеданс для пульсаций тока высокой частоты и поддерживать стабильное напряжение $ U_{DC} $.

6. Влияние частоты и высших гармоник на работу конденсаторов

В современной преобразовательной технике чистая синусоида — редкость. Работа ШИМ-инверторов и выпрямителей порождает спектр высших гармоник. Это критически влияет на ресурс конденсаторов.

Проблема перегрева: Потери в конденсаторе резко возрастают с частотой. Типовые графики показывают, что при увеличении частоты с 50 Гц до 10 кГц тангенс угла потерь может вырасти в 10 раз и более.

Расчет потерь мощности при несинусоидальном токе

Наиболее точный метод оценки теплового режима — суммирование потерь от каждой гармонической составляющей спектра. Активная мощность потерь $ P_C $ рассчитывается по формуле:

P_C = \sum_{n=1}^{\infty} (U_n^2 \cdot n \cdot \omega_1 \cdot C \cdot \tan \delta_n) \quad

Где:

$ n $ — номер гармоники;
$ \omega_1 $ — частота основной гармоники;
$ U_n $ — действующее (RMS) значение напряжения $ n $-й гармоники;
$ \tan \delta_n $ — значение тангенса угла потерь на частоте этой гармоники.

Увеличение частоты заставляет инженеров снижать допустимое рабочее напряжение на конденсаторе, чтобы избежать теплового пробоя.

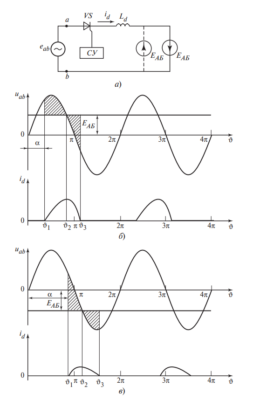
Зависимость допустимого напряжения от частоты (Описание Рис. 3)

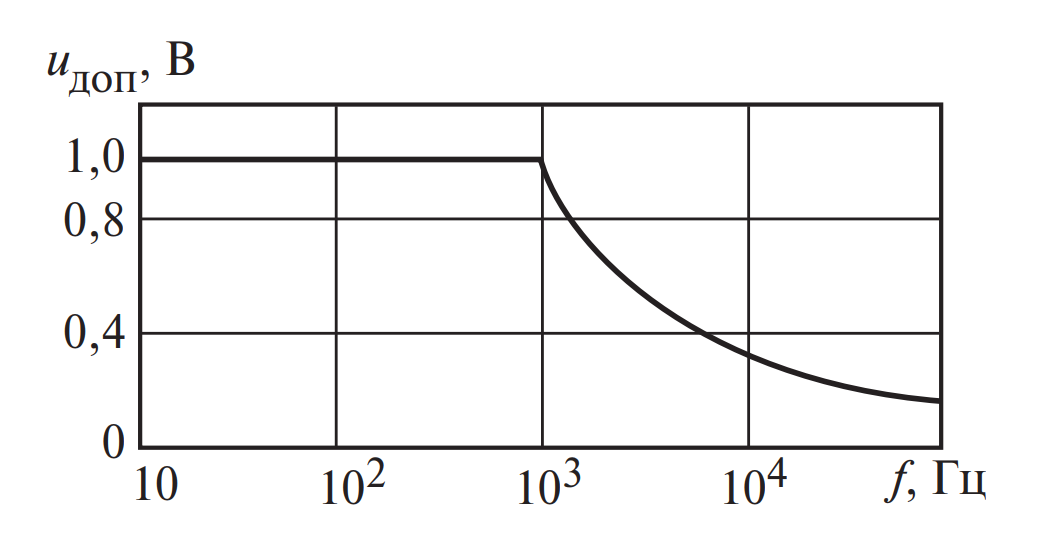
Рис. 3. Зависимость амплитуды допустимого напряжения конденсатора от частоты.

График на рис. 3 демонстрирует, как снижается допустимое напряжение $ U_{доп} $ с ростом частоты $ f $. При низких частотах ограничением является электрическая прочность диэлектрика (амплитуда пробоя). Однако с ростом частоты (обычно выше 1 кГц) кривая резко идет вниз. Это зона теплового ограничения: если не снизить напряжение, диэлектрик расплавится из-за внутренних потерь.

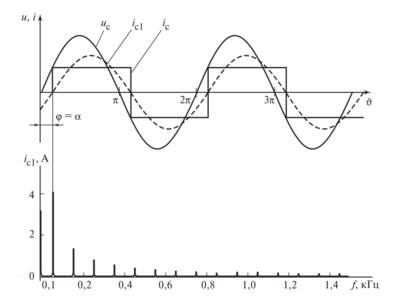
Оптимизация массогабаритных показателей (Описание Рис. 4)

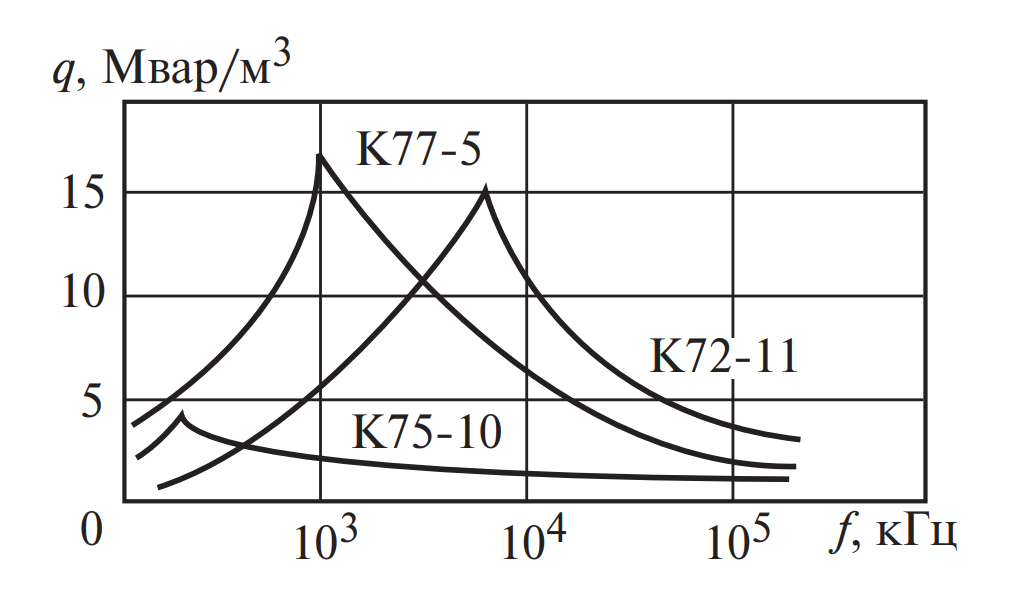
Рис. 4. Зависимость удельной реактивной мощности конденсаторов от частоты для различных типов (К77-5, К72-11, К75-10).

На рис. 4 показаны кривые удельной реактивной мощности (Мвар/м³) в зависимости от частоты. Видно, что для каждого типа диэлектрика существует свой пик эффективности. Это означает, что проектировщик должен подбирать тип конденсатора строго под рабочую частоту преобразователя, чтобы минимизировать объем устройства.

7. Импеданс электролитических конденсаторов на высоких частотах

Электролитические конденсаторы, несмотря на большую емкость, ведут себя на высоких частотах совсем не как конденсаторы. Это связано с наличием паразитной индуктивности выводов и рулона фольги.

Сложная схема замещения (Описание Рис. 5)

Рис. 5. а) Полная схема замещения электролитического конденсатора; б) Зависимость полного сопротивления $ Z_C $ от частоты для типа К50-20.

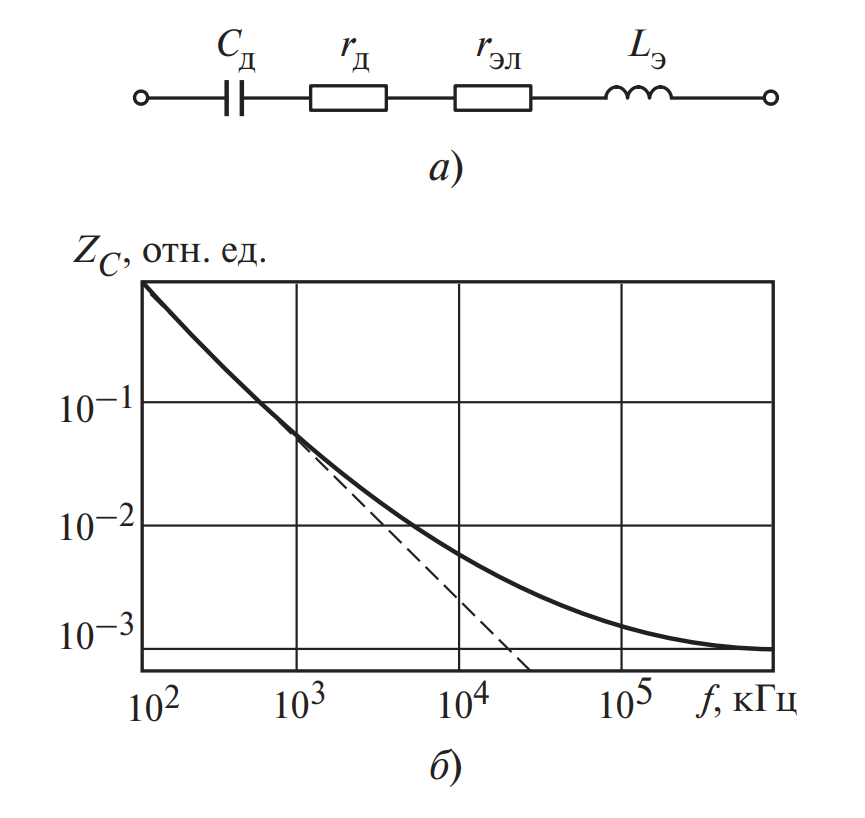
а) Схема замещения: Включает в себя:

$ C_д $ — собственная емкость диэлектрика.
$ r_д $ — сопротивление потерь в диэлектрике.
$ r_{эл} $ (в тексте $ r_э $) — сопротивление электролита и выводов (ESR).
$ L_э $ — эквивалентная последовательная индуктивность (ESL).

Полное сопротивление (импеданс) такого конденсатора описывается формулой:

Z_C = \sqrt{r_S^2 + \left( \frac{1}{2\pi f C_э} \cdot \frac{1}{1 — (f/f_0)^2} \right)^2} \quad

Где $ f_0 $ — частота собственного резонанса, определяемая как $ f_0 = \frac{1}{2\pi\sqrt{L_э C_д}} $.

б) Анализ графика: На графике (б) видно, что до определенной частоты импеданс падает (емкостной характер). В точке резонанса импеданс минимален и равен активному сопротивлению $ ESR $. При дальнейшем росте частоты (выше 10–20 кГц для К50-20) импеданс начинает расти! Конденсатор превращается в катушку индуктивности и перестает сглаживать пульсации.

Совет: Чтобы обойти этот эффект, в схемах параллельно мощному электролитическому конденсатору всегда ставят керамический или пленочный конденсатор малой емкости (0.1 – 1 мкФ). «Мелкий» конденсатор берет на себя фильтрацию ВЧ-помех, с которыми не справляется электролит из-за своей индуктивности.

Для оценки реальной эффективности на ВЧ используют понятие эффективной емкости:

C_{эф} = \frac{1}{2\pi f Z_C} \quad

8. Практический пример: Расчет конденсатора звена постоянного тока (DC-Link)

Для закрепления теоретического материала проведем расчет конденсатора фильтра для силовой установки. Это одна из самых распространенных задач при проектировании частотных преобразователей (ПЧ), источников питания и инверторов.

Постановка задачи:
Необходимо выбрать батарею электролитических конденсаторов для звена постоянного тока частотного преобразователя мощностью 15 кВт. Питание осуществляется от трехфазной сети 380 В / 50 Гц через мостовой выпрямитель Ларионова.

Исходные данные для расчета

Мощность нагрузки ($ P_{out} $): 15 000 Вт.
Линейное напряжение сети ($ U_{line} $): 380 В (AC).
Допустимый коэффициент пульсаций напряжения ($ K_p $): 2% (стандартное требование для надежной работы IGBT-модулей).
Температура внутри шкафа ($ T_{amb} $): +60 °C.
Планируемый срок службы: не менее 20 000 часов.

Этап 1: Определение рабочих напряжений и токов

Сначала найдем амплитудное значение выпрямленного напряжения. Для трехфазной схемы с мостовым выпрямителем среднее значение напряжения звена постоянного тока $ U_{DC} $ близко к амплитудному линейному:

U_{DC_{max}} = U_{line} \cdot \sqrt{2} = 380 \cdot 1.414 \approx 537 \text{ В}

С учетом возможных скачков напряжения в сети (+10%), конденсатор должен иметь номинальное напряжение с запасом. Выбираем стандартный ряд: $ U_{nom} = 400 \text{ В} $ (для последовательного соединения двух банок, итого 800 В) или одиночные на 600 В (редкость для больших емкостей).

Решение: Будем использовать последовательное включение двух групп конденсаторов по 400 В (суммарно 800 В), чтобы обеспечить запас прочности.

Рассчитаем средний ток потребления нагрузкой ($ I_{DC} $):

I_{DC} = \frac{P_{out}}{U_{DC}} = \frac{15000}{537} \approx 27.9 \text{ А}

Этап 2: Расчет необходимой емкости по допустимым пульсациям

При трехфазном выпрямлении частота пульсаций $ f_p $ составляет $ 6 \cdot f_{seti} = 300 \text{ Гц} $. Допустимый размах пульсаций $ \Delta U $ при требовании 2%:

\Delta U = U_{DC} \cdot 0.02 = 537 \cdot 0.02 \approx 10.7 \text{ В}

Минимальная емкость $ C_{min} $ определяется из условия, что конденсатор должен поддерживать ток нагрузки в паузах между пиками выпрямленного напряжения:

C_{min} \approx \frac{I_{DC}}{f_p \cdot \Delta U} = \frac{27.9}{300 \cdot 10.7} = 8.69 \cdot 10^{-3} \text{ Ф} \approx 8700 \text{ мкФ}

Так как мы решили использовать последовательное соединение двух групп (для получения 800 В), общая емкость батареи падает в 2 раза. Следовательно, каждая группа должна иметь емкость $ 2 \cdot C_{min} = 17400 \text{ мкФ} $.

Этап 3: Проверка по току пульсаций (Ripple Current) — Критический момент!

Это самый важный этап, который часто игнорируют начинающие инженеры. Конденсатор греется не от постоянного тока, а от переменной составляющей. Для трехфазного выпрямителя действующее значение тока пульсаций через конденсатор $ I_{C,rms} $ приближенно составляет 50-60% от тока нагрузки:

I_{C,rms} \approx 0.55 \cdot I_{DC} = 0.55 \cdot 27.9 \approx 15.3 \text{ А}

Выбор компонента: Рассмотрим, например, промышленный конденсатор 4700 мкФ x 400В (серия для силовой электроники).

Из даташита: $ Rated \ Ripple \ Current $ при 85°C и 100 Гц = 8.5 А.

Конфигурация батареи:

Нам нужно суммарно ~17400 мкФ в плече. 17400 / 4700 ≈ 3.7. Округляем до 4 параллельных конденсаторов.
Общая емкость плеча: $ 4 \cdot 4700 = 18800 \text{ мкФ} $ (Удовлетворяет $ C_{min} $).
Допустимый ток пульсаций всего плеча: $ 4 \cdot 8.5 \text{ А} = 34 \text{ А} $.

Так как расчетный ток пульсаций (15.3 А) меньше допустимого для сборки (34 А), конденсаторы не перегреются.

Этап 4: Тепловой расчет и оценка срока службы

Оценим реальный нагрев. Предположим, ESR (эквивалентное последовательное сопротивление) одного конденсатора составляет 30 мОм ($ 0.03 \text{ Ом} $).
Ток через один конденсатор: $ I_{cap} = 15.3 \text{ А} / 4 = 3.8 \text{ А} $.

Мощность потерь на одном конденсаторе:

P_{loss} = I_{cap}^2 \cdot ESR = 3.8^2 \cdot 0.03 \approx 0.43 \text{ Вт}

Это небольшое значение, корпус легко рассеет такое тепло. Перегрев $ \Delta T $ составит примерно 3–5 °C относительно среды.

При температуре внутри корпуса $ 60 \text{ °C} $ температура ядра конденсатора будет $ \approx 65 \text{ °C} $.

Закон Аррениуса для конденсаторов:
Срок службы электролитического конденсатора удваивается при снижении рабочей температуры на каждые 10 °C.Формула: $ L = L_0 \cdot 2^{\frac{T_{max} — T_{work}}{10}} $

Если базовый срок службы $ L_0 $ при 85 °C равен 5000 часов, то при нашей рабочей температуре 65 °C:

L = 5000 \cdot 2^{\frac{85 — 65}{10}} = 5000 \cdot 2^2 = 20 000 \text{ часов}

Вывод: Выбранная конфигурация (2 последовательные группы по 4 параллельных конденсатора 4700 мкФ x 400В) полностью удовлетворяет требованиям по пульсациям, токовой нагрузке и ресурсу.

9. Интересные факты о конденсаторах

Мир емкостных элементов полон удивительных физических явлений и неожиданных применений.

Планета-конденсатор. Земной шар вместе с ионосферой образует гигантский сферический конденсатор. Обкладками служат проводящая поверхность Земли и ионизированные слои атмосферы, а диэлектриком — нижние слои атмосферы. Напряжение между «обкладками» достигает 300–400 кВ, но из-за огромного расстояния напряженность поля у поверхности невелика (около 130 В/м). Постоянный заряд поддерживается грозовой активностью по всей планете.
«Поющие» конденсаторы. В современной электронике часто можно услышать тонкий писк от платы, даже если там нет динамиков. Виновники — многослойные керамические конденсаторы (MLCC). Обладая пьезоэлектрическим эффектом, диэлектрик (например, титанат бария) механически расширяется и сжимается в такт пульсациям напряжения. Если частота попадает в слышимый диапазон, плата начинает «петь».
Сенсорные экраны. Емкостная технология, используемая в каждом смартфоне, основана на теле человека как проводнике. Экран покрыт сеткой микроскопических конденсаторов. Когда вы касаетесь стекла пальцем, вы вносите дополнительную емкость в цепь утечки тока. Контроллер мгновенно вычисляет координаты изменения емкости, воспринимая это как касание. Стилусы для таких экранов работают, имитируя электрические свойства пальца.
Спасение жизней. В медицинских дефибрилляторах используется главный свойство конденсатора — способность мгновенно отдавать накопленную энергию. Батарейка заряжает конденсатор в течение нескольких секунд, а затем он разряжается за миллисекунды через электроды, создавая импульс мощностью в несколько киловатт, необходимый для перезапуска сердечного ритма.
Рельсотрон (Railgun). Военные электромагнитные пушки используют батареи конденсаторов размером с комнату. Чтобы разогнать снаряд до гиперзвуковых скоростей (более 2 км/с) с помощью силы Лоренца, требуется колоссальный импульс тока в миллионы ампер, который не может обеспечить ни один генератор напрямую, но легко выдает батарея импульсных конденсаторов.
Суперконденсаторы против аккумуляторов. Современные ионисторы (суперконденсаторы) занимают нишу между обычными конденсаторами и аккумуляторами. Они используют двойной электрический слой толщиной в несколько нанометров и пористые углеродные электроды с гигантской площадью поверхности. Это позволяет заряжать их за секунды и выдерживать сотни тысяч циклов перезаряда, что делает их идеальными для систем рекуперации энергии в транспорте.
Ошибка, стоившая истории. Первая «Лейденская банка» (прототип конденсатора) была открыта случайно и болезненно. В 1746 году Питер ван Мушенбрук пытался наэлектризовать воду в банке. Держа банку одной рукой (одна обкладка) и касаясь провода другой (вторая обкладка), он получил сильнейший удар током. Ученый написал: «Я не согласился бы пережить это еще раз даже за королевский трон Франции».

10. FAQ: Часто задаваемые вопросы (ЧаВо)

Ответы на самые популярные вопросы инженеров и радиолюбителей по эксплуатации конденсаторов.

В1: Можно ли заменить конденсатор на другой с большим или меньшим напряжением?

Ответ: Заменять на конденсатор с большим рабочим напряжением можно и даже полезно (увеличится надежность), главное, чтобы он подошел по габаритам. Заменять на конденсатор с меньшим напряжением категорически нельзя — это приведет к пробою диэлектрика, короткому замыканию и взрыву. Что касается емкости, то в цепях питания допускается увеличение на 20–50%, но в частотно-задающих цепях емкость должна быть строго номинальной.

В2: Почему вздуваются электролитические конденсаторы?

Ответ: Вздутие — это признак того, что жидкий электролит внутри закипел и начал испаряться, создавая избыточное давление. Это происходит из-за перегрева (внешнего или внутреннего из-за высокого ESR), превышения допустимого напряжения или переполюсовки. Насечки на верхней крышке корпуса — это специальный клапан безопасности, который разрывается, чтобы предотвратить разлет осколков корпуса при взрыве. Вздутый конденсатор подлежит немедленной замене.

В3: Что такое ESR и почему это самый важный параметр для ремонта?

Ответ: ESR (Equivalent Series Resistance) — эквивалентное последовательное сопротивление. Со временем электролит высыхает, емкость может оставаться в норме, но ESR растет. Это приводит к тому, что конденсатор перестает сглаживать пульсации и начинает сильно греться (по закону $ P = I^2 \cdot R $). Для импульсных блоков питания высокий ESR — главная причина выхода из строя, поэтому проверять старые конденсаторы нужно специальным ESR-метром, а не обычным мультиметром.

В4: Как правильно и безопасно разрядить высоковольтный конденсатор?

Ответ: Никогда не замыкайте выводы отверткой! Это создает огромный ток, который может приварить отвертку к контактам, повредить глаза искрами и разрушить внутреннюю структуру конденсатора. Для безопасного разряда используйте резистор номиналом 1–10 кОм мощностью 2–5 Вт, заизолированный в термоусадку. Подключите его к выводам на 5–10 секунд. В крайнем случае можно использовать лампу накаливания на 220 В.

В5: В чем разница между пусковым и рабочим конденсатором для электродвигателя?

Ответ: Пусковой конденсатор предназначен для кратковременной работы (несколько секунд) при старте двигателя. Он имеет большую емкость, но может перегреться и взорваться при длительном включении. Рабочий конденсатор постоянно включен в цепь фазосдвигающей обмотки, он рассчитан на непрерывный режим работы и высокие реактивные токи. Использовать пусковой электролитический конденсатор вместо рабочего пленочного (например, типа CBB60) запрещено.

Заключение

Конденсаторы остаются критически важным звеном в развитии силовой электроники. Несмотря на кажущуюся простоту, процессы, происходящие в них при высоких частотах и несинусоидальных токах, требуют глубокого понимания физики твердого тела и электродинамики. Современные тренды направлены на миниатюризацию, повышение рабочих температур и снижение паразитных индуктивностей, что позволяет создавать все более эффективные преобразователи энергии. Для студента и инженера крайне важно уметь работать не только с номинальной емкостью, но и с частотными характеристиками импеданса и потерь.

Нормативная база

ГОСТ IEC 60384-1-2015 — Конденсаторы постоянной емкости для электронной аппаратуры. Общие технические условия.
ГОСТ IEC 61071-2014 — Конденсаторы силовой электроники.
ГОСТ 12.2.007.5-75 — Система стандартов безопасности труда. Конденсаторы силовые. Установки конденсаторные. Требования безопасности.

Список литературы

Флоренцев, С. Н. Силовая электроника. Современное состояние и перспективы развития. — М.: МЭИ, 2018.
Уильямс, Б. В. Силовая электроника: приборы, драйверы, применения. — М.: Энергоатомиздат, 1993.
Техническая документация и Application Notes производителей компонентов (Epcos/TDK, Vishay, Kemet).