Характеристики выпрямителей: пульсации, коммутация и характеристики

Содержание страницы

1. Спектральный состав и пульсации выпрямленного напряжения
2. Влияние выпрямителя на питающую сеть: Искажение тока
3. Процесс коммутации: Микросекунды, которые решают всё
4. Внешние характеристики: Как выпрямитель держит нагрузку
5. Энергетическая эффективность и коэффициент мощности
6. Сравнительная характеристика схем выпрямления
7. Интересные факты о выпрямителях и коммутации
8. FAQ: Часто задаваемые вопросы по характеристикам выпрямителей
Заключение

Выпрямительные устройства — это основа современной силовой электроники. Их задача кажется тривиальной: преобразовать переменный ток (AC), который генерируется электростанциями, в постоянный ток (DC), необходимый для питания большинства электронных схем, электродвигателей постоянного тока и электрохимических установок. Однако за этой простотой скрывается сложный комплекс электромагнитных процессов.

История развития выпрямителей насчитывает более века: от громоздких вращающихся преобразователей и ртутных игнитронов до современных полупроводниковых тиристоров и транзисторов. Понимание характеристик выпрямителей — это не просто знание формул, это понимание того, как электрическая энергия меняет свою форму, какие потери при этом возникают и как этот процесс влияет на питающую сеть.

Суть проблемы: Идеальный выпрямитель должен выдавать чистую прямую линию напряжения и потреблять из сети чистую синусоиду тока. Реальный выпрямитель генерирует «грязное» пульсирующее напряжение и искажает ток сети. Наша задача — разобраться, почему это происходит и как это математически описать.

1. Спектральный состав и пульсации выпрямленного напряжения

Выпрямленное напряжение на выходе любого статического преобразователя никогда не бывает идеально гладким (как от аккумулятора). Оно всегда представляет собой пульсирующий поток энергии. С точки зрения математического анализа, это напряжение можно разложить на две составляющие:

Постоянная составляющая (DC): Полезная часть, которая совершает работу (например, вращает вал двигателя).
Переменная составляющая (AC): Вредная часть, называемая пульсацией. Она вызывает нагрев, вибрации, гул в аппаратуре и помехи.

Гармонический анализ напряжения

Переменная составляющая — это не хаотичный шум, а строгая сумма гармонических колебаний. Согласно теории рядов Фурье, мгновенное значение пульсации $ u_{\sim}(t) $ описывается уравнением:

\( u_{\sim}(t) = \sum_{n=1}^{\infty} U_{nm} \sin(n \omega t + \phi_n) \) (1) — Уравнение гармонического состава пульсаций

Где:

$ n $ — порядковый номер высшей гармоники.
$ m $ — пульсность схемы (количество пульсаций выходного напряжения за один период сетевого напряжения). Это фундаментальная характеристика топологии выпрямителя.
$ \omega $ — угловая частота питающей сети ($ \omega = 2\pi f $).
$ U_{nm} $ — амплитуда $ n $-й гармоники.
$ \phi_n $ — начальная фаза гармоники.

Аналогия: Представьте, что вы толкаете автомобиль. Постоянная составляющая — это скорость, с которой машина едет. Переменная составляющая (пульсации) — это рывки, с которыми вы толкаете машину. Чем чаще рывки (выше частота), тем плавнее кажется движение тяжелой машины (нагрузки), так как инерция сглаживает мелкие толчки.

Частотные характеристики

Важнейшим параметром для проектирования сглаживающих фильтров является частота гармоник. Она жестко привязана к частоте сети и пульсности схемы:

\( f_n = n f_1 = n m f \) (2) — Частота гармоник

Где $ f $ — частота сети (стандартно 50 Гц), а $ f_1 = mf $ — частота первой (основной) гармоники пульсаций. Рассмотрим это на примерах реальных схем при частоте сети 50 Гц:

Тип схемы	Пульсность (m)	Частота 1-й гармоники (n=1)	Сложность фильтрации
Однофазная двухполупериодная (мостовая)	2	100 Гц	Высокая (требуются большие конденсаторы/дроссели)
Трехфазная с нулевым выводом	3	150 Гц	Средняя
Трехфазная мостовая (схема Ларионова)	6	300 Гц	Низкая (пульсации мелкие и частые)

Амплитуда гармоник

Амплитуда гармоник показывает, насколько сильны пульсации. Для режима работы без задержки отпирания тиристоров (угол управления $ \alpha = 0 $), амплитуда $ n $-й гармоники определяется по формуле:

\( U_{nm} = \frac{2 U_{d0}}{m^2 n^2 — 1} \sqrt{1 + m^2 n^2 \dots} \) Примечание: В упрощенном виде зависимость убывающая.

Из анализа формулы (которая в общем виде показывает зависимость от квадрата номера гармоники) следует важный вывод: амплитуда гармоник убывает обратно пропорционально квадрату их номера. Это означает, что самой мощной и опасной является первая гармоника ($ n=1 $). Высшими гармониками (второй, третьей и т.д.) часто можно пренебречь, так как их энергия ничтожно мала.

Действующее значение переменной составляющей $ U_{\Pi} $ вычисляется как среднеквадратичное значение всех гармоник:

\( U_{\Pi} = \sqrt{\frac{1}{2} \sum_{n=1}^{\infty} U_{nm}^2} \) (3) — Действующее значение пульсаций

На практике качество выпрямленного напряжения оценивают через Коэффициент пульсаций $ K_{\Pi} $ — отношение амплитуды пульсаций к среднему выпрямленному напряжению.

Важно! При регулировании выпрямителя (увеличении угла $ \alpha $) ситуация ухудшается. С ростом угла задержки включения тиристоров переменная составляющая растет. Это логично: мы «вырезаем» куски из синусоиды, делая форму напряжения более резкой и прерывистой. Однако частота пульсаций (период повторяемости) от угла $ \alpha $ не зависит.

2. Влияние выпрямителя на питающую сеть: Искажение тока

Выпрямитель — это нелинейная нагрузка. В отличие от утюга или лампы накаливания, он потребляет ток не плавно по синусоиде, а импульсами. Это приводит к так называемому «загрязнению» электросети высшими гармониками тока.

Природа искажений

Идеальную синусоиду тока потребляет только однофазный выпрямитель при работе на чисто активную нагрузку (резистор) и угле $ \alpha = 0 $. Во всех остальных случаях, особенно при наличии индуктивности в нагрузке (дроссель, обмотка двигателя), ток приобретает прямоугольную или трапецеидальную форму.

Если индуктивность нагрузки $ L_d $ достаточно велика (режим непрерывного тока, $ \omega L_d \to \infty $), ток превращается в прямоугольные импульсы. Разложение такого тока в ряд Фурье для однофазной схемы дает выражение:

\( i_1(\vartheta) = \frac{4 I_d}{\pi k_T} \left( \sin \vartheta + \frac{1}{3}\sin 3\vartheta + \dots + \frac{1}{n}\sin n\vartheta \right) \) (4) — Гармонический состав тока

Где $ k_T $ — коэффициент трансформации.

Экспертный комментарий: Формула (4) показывает, что в спектре тока присутствуют только нечетные гармоники (3-я, 5-я, 7-я…). Особенно опасна 3-я гармоника в трехфазных сетях, так как токи третьей гармоники всех трех фаз совпадают по фазе и суммируются в нулевом проводе, что может привести к его перегреву и отгоранию даже при симметричной нагрузке.

Зависимость от характера нагрузки

Активная нагрузка: При увеличении угла управления $ \alpha $ (глубокое регулирование) токовая пауза увеличивается, форма тока становится более «острой», амплитуды высших гармоник растут.
Активно-индуктивная нагрузка: Индуктивность стремится поддержать ток постоянным. При идеально сглаженном токе на стороне DC, форма тока на стороне AC (прямоугольник) не меняется при изменении $ \alpha $. Меняется только фазовый сдвиг этого прямоугольника относительно напряжения (ухудшается коэффициент мощности).

Методы борьбы с искажениями

Для снижения вредного влияния на сеть используются фильтры. Они бывают пассивными (LC-цепи, настроенные на частоты гармоник) и активными (сложные электронные устройства, генерирующие «анти-гармоники»).

3. Процесс коммутации: Микросекунды, которые решают всё

В упрощенной теории часто предполагают, что ток мгновенно переключается с одного тиристора на другой. В реальности это невозможно. Причина — индуктивность рассеяния обмоток трансформатора $ L_s $. Индуктивность — это «электрическая инерция», она препятствует мгновенному изменению тока.

Процесс перехода тока с вентиля на вентиль называется коммутацией. Он занимает определенное время, в течение которого оба вентиля (уходящий из работы и вступающий в работу) открыты одновременно. Этот интервал характеризуется углом коммутации $ \gamma $.

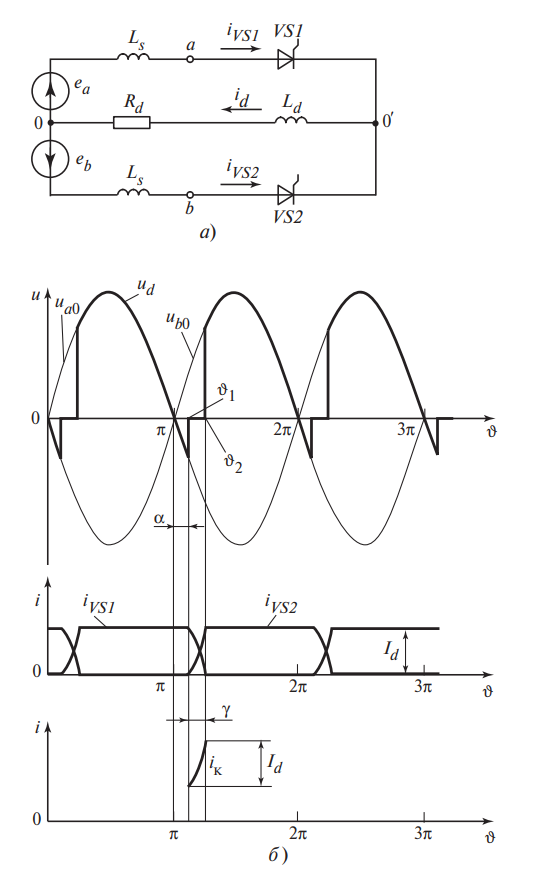
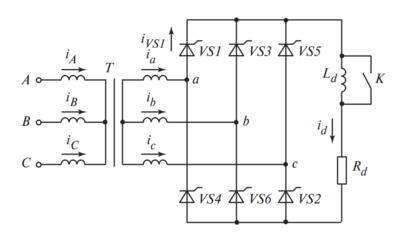
Рисунок 1. Двухполупериодный тиристорный выпрямитель и диаграммы коммутации.

Описание схемы (а): Показан трансформатор с двумя вторичными полуобмотками. Верхняя полуобмотка подключена к аноду тиристора VS1, нижняя — к аноду тиристора VS2. Катоды объединены и идут к нагрузке (Ld, Rd). В цепи анодов включены эквивалентные индуктивности рассеяния $ L_s $.
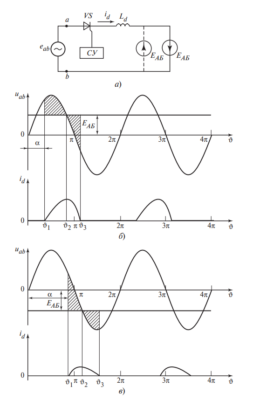
Описание диаграмм (б):

Верхний график: Синусоиды напряжения вторичных обмоток $ u_{a0} $ и $ u_{b0} $.
Средний график: Токи через тиристоры $ i_{VS1} $ и $ i_{VS2} $. Видно, что ток не падает мгновенно, а плавно снижается (для VS1) и плавно нарастает (для VS2) на участке $ \gamma $.
Нижний график: Выпрямленное напряжение $ u_d $. В момент коммутации (пересечение фаз) напряжение проседает до нуля.

Детальный разбор процесса (шаг за шагом)

Рассмотрим процесс на примере схемы со средним выводом (см. описание Рисунка 1), считая ток нагрузки идеально сглаженным ($ I_d = \text{const} $).

Исходное состояние: Проводит тиристор VS1. Ток нагрузки течет через верхнюю полуобмотку и VS1.
Момент $ \vartheta_1 $ (Включение): На тиристор VS2 подается импульс управления. Так как потенциал его анода выше катода, он открывается.
Интервал коммутации $ \gamma $:
- Теперь открыты оба тиристора (VS1 и VS2).
- Это означает, что вторичная обмотка трансформатора фактически замкнута накоротко через открытые тиристоры.
- Возникает ток короткого замыкания $ i_k $ в контуре, образованном двумя полуобмотками.
- Под действием разности ЭДС фаз ток в VS1 начинает убывать, а в VS2 — нарастать.
Математика тока КЗ:
Ток коммутации $ i_k $ состоит из вынужденной (установившейся) и свободной составляющих:
$$ i_k = \frac{U_2}{2x_s} [\cos \alpha — \cos(\vartheta + \alpha)] $ (5) — Ток коммутации$
Где $ x_s = \omega L_s $ — индуктивное сопротивление рассеяния.
Баланс токов: Сумма токов тиристоров всегда равна току нагрузки: $$ i_{VS1} + i_{VS2} = I_d = \text{const} $ (6) — Уравнение непрерывности тока$
Завершение коммутации: Как только ток $ i_{VS2} $ достигает значения $ I_d $, ток $ i_{VS1} $ становится равным нулю. Тиристор VS1 закрывается. Коммутация завершена.

Расчет угла коммутации

Длительность этого процесса (угол $ \gamma $) зависит от тока нагрузки, индуктивности рассеяния и угла управления. Основное уравнение коммутации:

\( I_d = \frac{U_2}{x_s} [\cos \alpha — \cos(\alpha + \gamma)] \) (7) — Связь тока нагрузки и угла коммутации

Из этого уравнения выводится формула для угла $ \gamma $:

\( \gamma = \arccos(\cos \alpha — \frac{x_s I_d}{U_2}) — \alpha \) (8)

Интересный факт: С увеличением угла управления $ \alpha $ угол коммутации $ \gamma $ уменьшается. Это связано с тем, что при больших углах $ \alpha $ коммутация происходит при большем мгновенном значении линейного напряжения (разности ЭДС фаз), которое «сильнее» проталкивает ток из одной фазы в другую, ускоряя процесс.

Влияние на выходное напряжение

Самое неприятное последствие коммутации — потеря напряжения. Пока оба тиристора открыты (КЗ вторичной цепи), мгновенное напряжение на выходе равно полусумме напряжений фаз (для мостовой схемы) или нулю (для схемы с нулевой точкой при определенных условиях). В любом случае, среднее значение напряжения снижается. Эта потеря обозначается как $ \Delta U_x $:

\( \Delta U_x = \frac{1}{\pi} \int_{\alpha}^{\alpha+\gamma} U_2 \sin \vartheta \, d\vartheta = \frac{I_d x_s}{\pi} \) (9) — Индуктивное падение напряжения

Итоговая формула среднего напряжения с учетом коммутации:

\( U_d = U_{d0} \cos \alpha — \frac{I_d x_s}{\pi} \) (10)

4. Внешние характеристики: Как выпрямитель держит нагрузку

Внешняя характеристика — это зависимость выходного напряжения $ U_d $ от тока нагрузки $ I_d $. Для идеального источника эта линия была бы горизонтальной. Для реального выпрямителя она падающая.

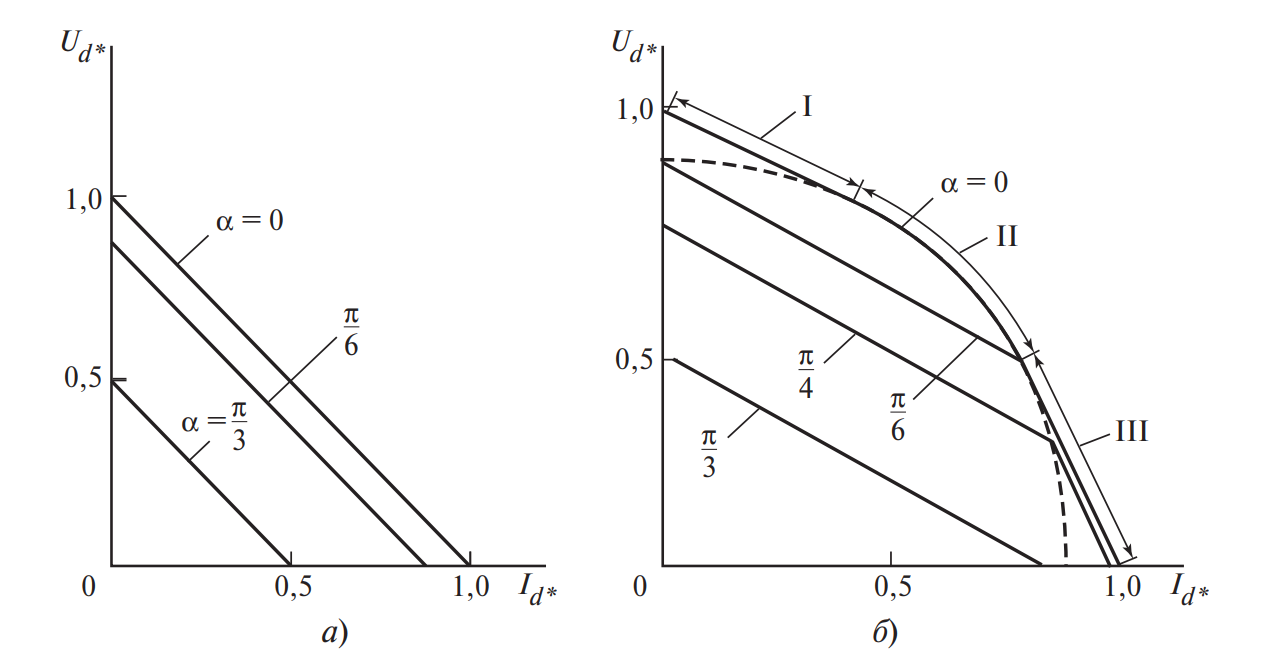
Рисунок 2. Внешние характеристики выпрямителей.

Описание (а): График для однофазного выпрямителя. По оси Y — относительное напряжение $ U_d^* $, по оси X — ток $ I_d^* $. Линии идут вниз под наклоном. Показаны семейства кривых для разных углов $ \alpha $ (0, 30, 60 градусов).
Описание (б): График для трехфазного мостового выпрямителя. Характер падения более крутой в зоне перегрузок.

Уравнение внешней характеристики учитывает три фактора потерь:

\( U_d = U_{d0} \cos \alpha — \Delta U_R — \Delta U_{VS} — \Delta U_x \) (11) — Полное уравнение внешней характеристики

Расшифровка потерь:

$ \Delta U_R $ (Активные потери): Падение напряжения на активном сопротивлении обмоток трансформатора, проводов и шин. Преобладает в выпрямителях малой мощности.
$ \Delta U_{VS} $ (Падение на вентилях): Пороговое напряжение полупроводников (около 1-1.5 В на тиристор). В высоковольтных схемах малозаметно, в низковольтных — критично.
$ \Delta U_x $ (Индуктивное падение): То самое снижение напряжения из-за коммутации, которое мы разобрали выше. Преобладает в мощных преобразователях.

В нормальных режимах падение напряжения составляет 5-10%. Однако при перегрузках или КЗ характеристика резко падает вниз, так как индуктивное сопротивление начинает играть доминирующую роль.

5. Энергетическая эффективность и коэффициент мощности

Эффективность выпрямителя оценивается не только тем, сколько энергии он передал, но и тем, сколько он «испортил» в процессе.

Коэффициент полезного действия (КПД)

КПД ($ \eta $) определяется классическим отношением полезной мощности к затраченной.

\( \eta = \frac{U_d I_d}{U_d I_d + \Delta P_T + \Delta P_{VS} + \Delta P_{всп}} \) (12) — Формула КПД

Современные мощные тиристорные выпрямители имеют очень высокий КПД (0.9 – 0.98), так как потери в полупроводниках относительно малы по сравнению с передаваемой мощностью.

Коэффициент мощности (Power Factor)

Здесь все сложнее, чем в обычных цепях переменного тока. Коэффициент мощности $ \chi $ для выпрямителя зависит от двух факторов:

Фазовый сдвиг ($ \cos \phi_1 $): Обусловлен углом управления $ \alpha $ и индуктивностью коммутации. Чем больше мы «задерживаем» открытие тиристора, тем больше ток отстает от напряжения.
Коэффициент искажения ($ \nu $): Обусловлен несинусоидальностью тока. Так как ток не является синусоидой, полная мощность $ S $ содержит мощность гармоник, которая не совершает полезной работы.

Формула для выпрямителя с идеально сглаженным током:

\( \chi = \nu \cdot \cos \alpha \) (13) — Коэффициент мощности управляемого выпрямителя

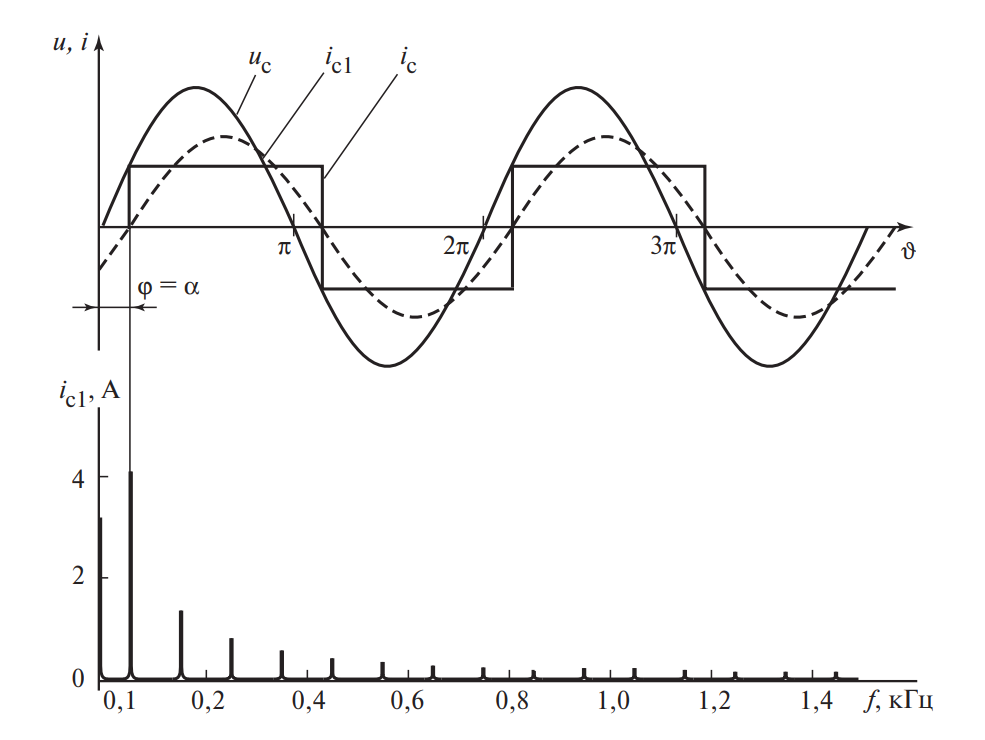
Рисунок 3. Диаграммы напряжения и тока сети.

Показана синусоида напряжения сети $ u_c $ и прямоугольная (ступенчатая) форма тока $ i_c $. Выделена первая гармоника тока $ i_{c1} $, которая сдвинута относительно напряжения на угол $ \phi_1 $. Этот сдвиг примерно равен углу управления $ \alpha $.

Вывод: Управляемый выпрямитель всегда потребляет из сети значительную реактивную мощность (даже при активной нагрузке!), причем чем глубже регулирование (ниже выходное напряжение), тем хуже коэффициент мощности. Это требует установки компенсирующих устройств (конденсаторных батарей) на входе.

6. Сравнительная характеристика схем выпрямления

Параметр	Однофазная мостовая	Трехфазная с нулевым выводом	Трехфазная мостовая (Ларионова)
Количество вентилей	4	3	6
Частота пульсаций (f сети = 50 Гц)	100 Гц	150 Гц	300 Гц
Коэфф. пульсаций (без фильтра)	67%	25%	5.7%
Использование мощности трансформатора	Хорошее	Плохое (подмагничивание)	Отличное
Обратное напряжение на вентиле	1.57 $ U_d $	2.09 $ U_d $	1.05 $ U_d $

7. Интересные факты о выпрямителях и коммутации

Легализованное короткое замыкание. Процесс коммутации, который происходит в выпрямителе сотни раз в секунду, технически является коротким замыканием вторичной обмотки трансформатора. В этот момент (угол $\gamma$) ток течет сразу через две фазы, минуя нагрузку, но благодаря индуктивности рассеяния это не приводит к аварии, а лишь «переливает» энергию.
Ртутные предки. До появления кремниевых тиристоров в середине XX века использовались гигантские ртутные выпрямители (игнитроны). Они излучали жутковатое фиолетовое свечение и были настолько надежны, что некоторые работали на подстанциях метрополитена и алюминиевых заводах более 50 лет.
Парадокс угла управления. При увеличении угла задержки открытия тиристоров ($\alpha$) длительность процесса коммутации ($\gamma$) на самом деле уменьшается. Это происходит потому, что коммутация начинается при более высоком мгновенном напряжении между фазами, которое быстрее «проталкивает» ток из одного плеча в другое.
Эффект «поющих» шин. Мощные выпрямители заставляют токоведущие шины и трансформаторы издавать характерный гул. Это вызвано магнитострикцией — физической деформацией сердечников под действием высших гармоник тока (особенно 300 Гц, 600 Гц). Опытный инженер может на слух определить степень загрузки выпрямителя.
Математическая хитрость Ларионова. Изобретенная в 1923 году схема «три параллельных моста» (известная как схема Ларионова) стала стандартом де-факто для всего мира. Её гениальность в том, что она естественным образом подавляет все гармоники, кратные трем, без использования каких-либо фильтров.
Угроза нулевому проводу. В офисных зданиях с большим количеством компьютерных блоков питания (которые являются выпрямителями) ток в нулевом проводе может превышать ток в фазах. Это происходит из-за суммирования токов третьей гармоники (150 Гц), которые совпадают по фазе, создавая риск пожара даже при «нормальной» нагрузке.
Псевдо-синусоида 24 пульса. В сверхмощных приводах (например, на ледоколах) используют 12-ти и 24-х пульсные схемы выпрямления. Для этого применяют трансформаторы со смещением фаз обмоток (звезда и треугольник). В результате входной ток становится настолько близким к синусоиде, что фильтры практически не нужны.

8. FAQ: Часто задаваемые вопросы по характеристикам выпрямителей

1. Почему выходное напряжение выпрямителя падает при подключении нагрузки?

Это происходит из-за внутреннего сопротивления выпрямителя. Оно складывается из трех факторов: активного сопротивления обмоток, падения напряжения на полупроводниках (около 1–2 В) и, самое главное, индуктивного падения напряжения ($\Delta U_x$). Последнее вызвано процессом коммутации: чем больше ток нагрузки, тем дольше длится переключение вентилей, «съедая» часть полезной площади синусоиды напряжения.

2. Что произойдет, если индуктивность рассеяния трансформатора будет равна нулю?

В теоретической идеальной модели процесс коммутации станет мгновенным ($\gamma = 0$). Внешняя характеристика станет более жесткой (напряжение будет падать меньше). Однако в реальности это привело бы к бесконечно большим скоростям нарастания тока ($di/dt$) при включении тиристоров, что мгновенно вывело бы полупроводники из строя из-за теплового пробоя кристалла. Индуктивность рассеяния играет роль защитного буфера.

3. В чем разница между выпрямителем напряжения и выпрямителем тока?

Различие кроется в типе выходного фильтра. Если на выходе стоит конденсатор большой емкости, устройство стремится поддерживать неизменное напряжение (выпрямитель напряжения). Если же используется мощный дроссель (индуктивность), устройство поддерживает неизменный ток (выпрямитель тока). Промышленные схемы большой мощности чаще всего являются выпрямителями тока из-за необходимости сглаживания глубоких пульсаций.

4. Как угол управления $\alpha$ влияет на коэффициент мощности ($\chi$)?

Влияние прямое и негативное. При фазовом управлении тиристорами мы искусственно сдвигаем момент потребления тока относительно напряжения сети. Коэффициент мощности приблизительно равен $\chi \approx \nu \cdot \cos \alpha$. Чем глубже мы регулируем выпрямитель (уменьшаем выходное напряжение), тем сильнее отстает ток, и тем больше реактивной (бесполезной) мощности потребляется из сети.

5. Можно ли избавиться от пульсаций на 100%?

Полностью избавиться от переменной составляющей невозможно, но можно свести её к пренебрежимо малым значениям. Для этого увеличивают пульсность схемы (переход с 1-фазной на 3-фазную снижает пульсации с 67% до 5.7%) и используют многозвенные LC-фильтры. В прецизионной аппаратуре после выпрямителя ставят линейный стабилизатор, который активно «срезает» остаточные пульсации.

Заключение

Понимание характеристик выпрямителей требует комплексного подхода, учитывающего как временные диаграммы, так и спектральный состав сигналов. Ключевым моментом для инженера является осознание компромиссов: улучшение сглаживания пульсаций требует удорожания фильтров, а регулирование выходного напряжения неизбежно ведет к ухудшению коэффициента мощности и росту реактивных потерь. Процесс коммутации, обусловленный индуктивностью рассеяния трансформатора, является фундаментальным ограничением, снижающим выходное напряжение под нагрузкой и накладывающим предел на быстродействие защиты преобразователя. Грамотный учет этих факторов позволяет создавать надежные системы электропитания, соответствующие современным жестким требованиям по энергоэффективности и электромагнитной совместимости.

Нормативная база

При проектировании и эксплуатации выпрямительных установок необходимо руководствоваться следующими действующими стандартами:

ГОСТ 32144-2013 — Нормы качества электрической энергии (ограничение гармоник тока).
ГОСТ 24607-88 — Преобразователи частоты полупроводниковые. Общие технические требования.

Список рекомендуемой литературы

Розанов Ю. К., Рябчицкий М. В., Кваснюк А. А. Силовая электроника: учебник для вузов. — 2-е изд., стереотип. — М.: Издательский дом МЭИ, 2015. — 632 с.
Зиновьев Г. С. Основы силовой электроники: Учебник. — 5-е изд., испр. и доп. — М.: Юрайт, 2016. — 670 с.