Экспериментальное определение параметров индуктивной катушки: метод амперметра-вольтметра-ваттметра

Содержание страницы

Теоретические основы метода
Схема экспериментальной установки
Расчет параметров по результатам измерений
Векторные диаграммы и треугольники
Определение характера неизвестного двухполюсника
Сравнение методов измерения параметров катушек
Интересные факты об индуктивных катушках и их измерении
Часто задаваемые вопросы (FAQ)
Заключение

Реальные индуктивные элементы в электротехнических цепях никогда не являются идеальными. Они всегда обладают активным сопротивлением провода обмотки, а при наличии сердечника — и потерями на гистерезис и вихревые токи. Точное определение этих паразитных параметров критически важно для проектирования фильтров, трансформаторов, электрических машин и корректного расчета режимов цепей переменного тока. В данной статье рассматривается классический лабораторный метод определения параметров катушки без ферромагнитного сердечника на промышленной частоте.

Теоретические основы метода

Любая реальная индуктивная катушка при включении в цепь синусоидального переменного тока обладает не только индуктивностью $L$, но и активным сопротивлением $R$. Если катушка не имеет ферромагнитного сердечника (является «воздушной»), ее параметры $R$ и $L$ можно считать линейными, то есть независящими от величины протекающего тока. В этом случае схема замещения катушки представляется в виде последовательного соединения идеального активного резистора и идеальной индуктивности.

Физически разделить эти элементы невозможно, так как они распределены по всей длине провода намотки. Чтобы подчеркнуть эту неразрывность, на принципиальных схемах их иногда заключают внутри пунктирного прямоугольника (см. Рисунок 1).

Для экспериментального определения этих параметров применяется метод трех приборов: амперметра, вольтметра и ваттметра. Этот метод основан на измерении действующих значений тока и напряжения, а также активной мощности, потребляемой исследуемым двухполюсником.

Схема экспериментальной установки

Сборка измерительной цепи производится согласно схеме, представленной на Рисунке 1. В цепь последовательно с исследуемой катушкой включаются токовая обмотка ваттметра и амперметр. Параллельно катушке подключаются обмотка напряжения ваттметра и вольтметр.

Электрическая схема: источник переменного напряжения ~U подключен к цепи, состоящей из последовательно соединенных амперметра (PA), токовой обмотки ваттметра (PW) и исследуемой катушки (представленной как R и L в пунктирном прямоугольнике). Вольтметр (PV) и обмотка напряжения ваттметра подключены параллельно исследуемой катушке.

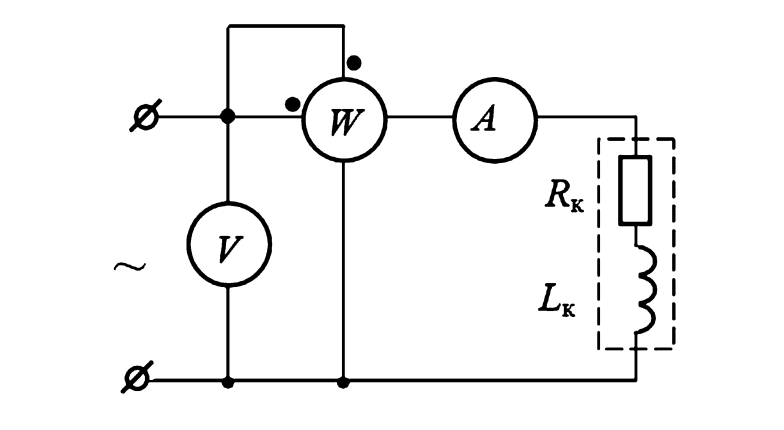
Рисунок 1 — Схема электрической цепи для определения параметров катушки индуктивности

Важное замечание по выбору приборов: Для измерений в цепях переменного тока промышленной частоты (50 Гц) традиционно используются приборы электромагнитной или электродинамической системы. Они измеряют истинное действующее (среднеквадратичное) значение тока $I$ и напряжения $U$. Магнитоэлектрические приборы (без выпрямителей) реагируют только на постоянную составляющую и в данной схеме покажут ноль. Современные цифровые мультиметры должны иметь функцию «True RMS» для корректных показаний, если форма тока отличается от идеальной синусоиды.

Особенности подключения ваттметра

Ваттметр — прибор электродинамической (или ферродинамической, цифровой) системы, имеющий две измерительные цепи:

Токовая обмотка: имеет малое сопротивление, включается последовательно с нагрузкой.
Обмотка напряжения: имеет большое сопротивление, включается параллельно нагрузке.

Для правильного измерения важно соблюдать полярность включения обмоток. Начала обмоток («генераторные зажимы») на корпусе прибора обозначаются точками $(\bullet)$ или звездочками $(*)$. Они должны подключаться со стороны источника питания.

Расчет параметров по результатам измерений

Ваттметр измеряет активную мощность $P$, которая в цепи переменного тока определяется формулой:

$$ P = U \cdot I \cdot \cos\phi $$

где $\phi$ — угол сдвига фаз между напряжением и током.

Используя показания приборов (мощность $P$, напряжение $U$, ток $I$), можно определить все основные параметры катушки, пользуясь следующими соотношениями:

1. Полное сопротивление (импеданс)

Согласно закону Ома для цепи переменного тока, полное сопротивление $Z$ равно отношению действующего значения напряжения к действующему значению тока:

$$ Z = \frac{U}{I} $$

2. Активное сопротивление

Активная мощность выделяется только на активном сопротивлении $R$. Следовательно, его можно найти из формулы мощности $P = I^2 \cdot R$:

$$ R = \frac{P}{I^2} $$

3. Коэффициент мощности

Коэффициент мощности $\cos\phi$ показывает отношение полезной (активной) мощности $P$ к полной мощности $S = U \cdot I$:

$$ \cos\phi = \frac{P}{S} = \frac{P}{U \cdot I} $$

Зная $\cos\phi$, можно найти активное сопротивление и другим способом: $R = Z \cdot \cos\phi$.

4. Реактивное (индуктивное) сопротивление

Используя треугольник сопротивлений (см. Рисунок 2б), индуктивное сопротивление $X_L$ можно найти по теореме Пифагора:

$$ X_L = \sqrt{Z^2 — R^2} $$

Альтернативный способ через тригонометрические функции: $X_L = Z \cdot \sin\phi$, где $\sin\phi = \sqrt{1 — \cos^2\phi}$.

5. Индуктивность катушки

Зная индуктивное сопротивление и частоту сети $f$ (для промышленной сети $f = 50$ Гц), вычисляем индуктивность $L$:

$$ L = \frac{X_L}{\omega} = \frac{X_L}{2\pi f} $$

где $\omega$ — угловая частота.

Векторные диаграммы и треугольники

Для графического представления соотношений в исследуемой цепи строят векторные диаграммы и треугольники, показанные на Рисунке 2.

Диаграммы: а) Векторная диаграмма напряжений: горизонтальный вектор тока I, совпадающий с ним по фазе вектор активного напряжения Ua = I*R, и опережающий его на 90 градусов вектор индуктивного напряжения UL = I*XL. Сумма векторов Ua и UL дает вектор полного напряжения U, сдвинутый относительно тока на угол phi.
б) Треугольник сопротивлений: прямоугольный треугольник с катетами R (горизонтальный) и XL (вертикальный) и гипотенузой Z. Угол между R и Z равен phi.
в) Треугольник мощностей: подобный треугольнику сопротивлений, с катетами P (активная мощность) и Q (реактивная мощность), и гипотенузой S (полная мощность).

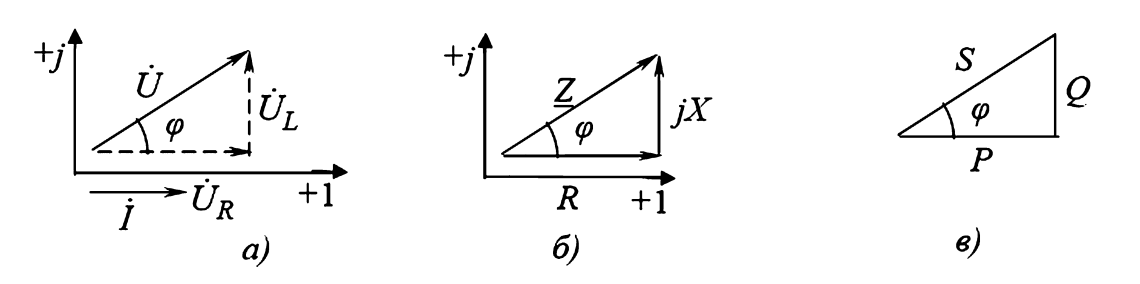
Рисунок 2 — Векторные диаграммы и треугольники: а — векторная диаграмма напряжений; б — треугольник сопротивлений; в — треугольник мощностей.

а) Векторная диаграмма напряжений: показывает, что полное напряжение $\vec{U}$ является векторной суммой активной составляющей $\vec{U}_R$ (совпадающей по фазе с током) и индуктивной составляющей $\vec{U}_L$ (опережающей ток на 90°).
б) Треугольник сопротивлений: получается из диаграммы напряжений делением всех сторон на ток $I$. Наглядно демонстрирует связь $Z^2 = R^2 + X_L^2$.
в) Треугольник мощностей: получается умножением сторон треугольника напряжений на ток $I$. Связывает полную $S$, активную $P$ и реактивную $Q$ мощности: $S^2 = P^2 + Q^2$.

Определение характера неизвестного двухполюсника

Описанный метод универсален и подходит для любого пассивного двухполюсника. Однако, если мы имеем «черный ящик», базовые измерения $P, U, I$ дадут нам модуль реактивного сопротивления $X = \sqrt{Z^2 — R^2}$, но не его знак (индуктивный или емкостный).

Чтобы определить характер реактивности, необходимо провести дополнительный опыт: включить последовательно с исследуемым двухполюсником конденсатор известной емкости. Если после этого общее реактивное сопротивление цепи уменьшится, значит, исходный двухполюсник имел активно-индуктивный характер (емкость частично скомпенсировала индуктивность). Если же реактивное сопротивление возрастет — двухполюсник имел активно-емкостный характер.

Сравнение методов измерения параметров катушек

Метод амперметра-вольтметра-ваттметра является базовым, но не единственным. Сравним его с другими распространенными методами.

Таблица 1 — Сравнение методов измерения параметров индуктивных катушек
Метод	Преимущества	Недостатки
Метод амперметра-вольтметра-ваттметра	Измерение в реальном рабочем режиме (под номинальным током/напряжением). Простота реализации на промышленной частоте. Учет реальных потерь (включая потери в стали, если есть сердечник).	Невысокая точность при малых значениях $\cos\phi$ (большая фазовая погрешность ваттметров). Необходимость учета собственного потребления приборов для точных измерений.
Мостовой метод (мосты переменного тока)	Высокая точность измерений. Возможность измерения малых индуктивностей и добротностей.	Сложность процесса балансировки моста. Измерения проводятся обычно на малых токах, что может не отражать реальные параметры нелинейных катушек.
Резонансный метод (Q-метр)	Идеален для высокочастотных катушек. Прямое измерение добротности $Q$.	Менее пригоден для низкочастотных силовых катушек. Требует специализированного оборудования.

Интересные факты об индуктивных катушках и их измерении

Неидеальность «воздуха»: Даже у катушки без ферромагнитного сердечника индуктивность может незначительно зависеть от частоты из-за поверхностного эффекта (скин-эффекта) в проводах, который уменьшает эффективное сечение проводника на высоких частотах.
Паразитная емкость: Любая реальная катушка имеет межвитковую емкость. На определенной (собственной резонансной) частоте катушка превращается в колебательный контур и может вести себя как активное сопротивление или даже как емкость.
Влияние ваттметра: Классический электродинамический ваттметр сам потребляет мощность. В точных лабораторных работах из измеренной мощности $P_{изм}$ вычитают мощность, потребляемую обмоткой напряжения самого ваттметра ($U^2/R_V$) и вольтметра.
Косинус фи и погрешность: При измерениях катушек с очень высокой добротностью (угол $\phi$ близок к 90°, $\cos\phi$ близок к 0) погрешность ваттметра резко возрастает. Для таких измерений существуют специальные малокосинусные ваттметры.
Стандарт индуктивности: Эталоны индуктивности (взаимоиндуктивности) выполняются исключительно без ферромагнитных сердечников, часто на каркасах из мрамора или специальной керамики, для обеспечения высочайшей стабильности во времени и независимости от внешних полей.
Температурный дрейф: Активное сопротивление $R$ медной обмотки увеличивается примерно на 0.4% при повышении температуры на 1°C. Поэтому измерения следует проводить в установившемся тепловом режиме.
Бифилярная намотка: Существует способ намотки катушки (бифилярная), при котором ее индуктивность практически равна нулю. Такие катушки применяются для создания проволочных резисторов с минимальной паразитной реактивностью.

Часто задаваемые вопросы (FAQ)

Вопрос 1: Можно ли использовать этот метод для катушки с железным сердечником?

Да, метод применим, но с оговоркой. Для катушки с сердечником параметры $L$ и $R$ станут нелинейными (зависящими от тока). Измеренные значения будут справедливы только для конкретного значения тока, при котором проводился опыт. Полученное $R$ будет включать в себя не только сопротивление провода, но и эквивалентное сопротивление потерь в стали сердечника.

Вопрос 2: Почему нельзя просто измерить активное сопротивление R мультиметром в режиме омметра?

Омметр на постоянном токе измерит только омическое сопротивление провода ($R_{DC}$). На переменном токе реальное активное сопротивление ($R_{AC}$) всегда выше из-за скин-эффекта, эффекта близости и возможных потерь в окружающих металлических предметах (вихревые токи). Метод ваттметра дает именно реальное $R_{AC}$ на рабочей частоте.

Вопрос 3: Что будет, если перепутать полярность токовой обмотки ваттметра?

Стрелка аналогового ваттметра отклонится в обратную сторону (за ноль), что может повредить прибор. Цифровой ваттметр просто покажет отрицательное значение мощности.

Вопрос 4: В каких единицах получаются результаты при расчетах по приведенным формулам?

Если напряжение подставлять в Вольтах [В], ток в Амперах [А], а мощность в Ваттах [Вт], то сопротивления $R, Z, X_L$ будут в Омах [Ом], а индуктивность $L$ — в Генри [Гн].

Вопрос 5: Как влияет класс точности приборов на результат?

Напрямую. Относительная погрешность определения $R$ и $X_L$ примерно равна удвоенной сумме приведенных погрешностей используемых приборов. Для лабораторных работ рекомендуется использовать приборы класса точности 0.5 или 1.0.

Вопрос 6: Зачем нужен вольтметр, если у ваттметра уже есть обмотка напряжения?

Ваттметр показывает только мощность (произведение $U \cdot I \cdot \cos\phi$). Чтобы найти полные сопротивление $Z = U/I$ и затем разделить его на $R$ и $X_L$, нам обязательно нужно знать отдельные значения $U$ и $I$.

Вопрос 7: Безопасно ли размыкать цепь тока во время работы ваттметра?

Размыкать вторичные цепи измерительных трансформаторов тока категорически запрещено. В прямых схемах включения (как на Рис. 1) при небольших напряжениях размыкание допустимо, но не рекомендуется под нагрузкой во избежание возникновения дуги. Все переключения лучше делать при снятом напряжении.

Заключение

Экспериментальное определение параметров индуктивной катушки методом трех приборов является классической и надежной методикой, широко применяемой в электротехнике. Несмотря на появление современных цифровых RLC-измерителей, данный метод остается незаменимым при испытаниях силового оборудования, так как позволяет определять параметры элементов в режимах, максимально приближенных к эксплуатационным — при реальных значениях рабочих токов и напряжений промышленной частоты.

Нормативная база и литература

ГОСТ IEC 60051-1-2021 Приборы аналоговые показывающие электроизмерительные прямого действия и вспомогательные части к ним. Часть 1. Определения и основные требования, общие для всех частей.
ГОСТ 19880-74 Электротехника. Основные понятия. Термины и определения.
Правила устройства электроустановок (ПУЭ), Глава 1.1. Общая часть.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2023.