Интеграл Дюамеля: расчет переходных процессов, формула, пример

Содержание страницы

Временные характеристики линейных цепей
Вывод интеграла Дюамеля
Преимущества и недостатки метода
Сравнение методов анализа переходных процессов
Пример 1. Расчет тока в RL-цепи
Интересные факты об интеграле Дюамеля
Часто задаваемые вопросы (FAQ)
Заключение

Интеграл Дюамеля (также известный как интеграл свертки) — это главный математический инструмент, используемый в теории линейных систем, включая электротехнику, для определения реакции (например, тока или напряжения) цепи на воздействие произвольной, сложной формы. Метод позволяет рассчитать переходный процесс в линейной цепи при любом непериодическом входном напряжении, зная реакцию этой цепи на простое единичное ступенчатое воздействие.

Метод был разработан французским математиком Жаном-Мари Констаном Дюамелем в XIX веке, изначально для решения задач теплопроводности. Позже его принцип был адаптирован для анализа любых линейных систем, описываемых дифференциальными уравнениями, что сделало его незаменимым в теории электрических цепей.

Временные характеристики линейных цепей

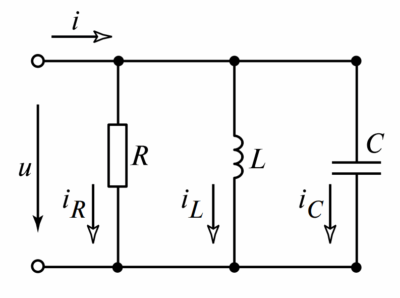
В линейных электрических цепях, благодаря принципу суперпозиции, ток в любой k-й ветви (\(i_k\)) может быть представлен как произведение напряжения на входе n-й ветви (\(U_n\)) на соответствующую входную (\(g_{kk}\)) или взаимную (\(g_{kn}\)) проводимость:

\(i_k = U_n \cdot g_{kn}\)

При анализе переходных процессов, когда цепь подключается к источнику постоянного напряжения, это соотношение сохраняется. Однако в этом случае и ток, и проводимость становятся функциями времени:

\(i_k(t) = U_n \cdot g_{kn}(t)\)

Здесь \(\boldsymbol{g_{kn}(t)}\) называется переходной проводимостью. В общем случае, переходная проводимость \(\boldsymbol{g_{kn}(t)}\) определяется как отношение переходного тока в k-й ветви к постоянному напряжению в n-й ветви, при условии отсутствия других источников в цепи и нулевых начальных условиях:

\(g_{kn}(t) = \frac{i_k(t)}{U_n}\) (1)

Аналогично, напряжение на любом участке цепи \(\boldsymbol{ab}\) во время переходного процесса также является функцией времени и пропорционально воздействующему напряжению \(\boldsymbol{U}\):

\(u_{ab}(t) = U \cdot k(t)\)

где \(\boldsymbol{k(t)}\) — переходная функция напряжения. Она определяется как отношение напряжения \(\boldsymbol{u_{ab}(t)}\) к входному напряжению \(\boldsymbol{U}\) при отсутствии в цепи других источников.

Для стандартизации и упрощения расчетов, переходную проводимость \(\boldsymbol{g(t)}\) и переходную функцию \(\boldsymbol{k(t)}\) обычно определяют, используя единичное ступенчатое воздействие, то есть при \(\boldsymbol{U = 1 \text{ В}}\). Эти функции \(\boldsymbol{g(t)}\) и \(\boldsymbol{k(t)}\) объединяют под общим названием временные характеристики цепи (или функции отклика на единичную ступень), обозначаемые \(\boldsymbol{h(t)}\).

Вывод интеграла Дюамеля

Основная задача, решаемая интегралом Дюамеля, — определение тока \(\boldsymbol{i(t)}\) или напряжения \(\boldsymbol{u(t)}\) на участке цепи при включении этой цепи под напряжение сложной, произвольной формы \(\boldsymbol{u(\tau)}\), при условии, что временная характеристика (например, \(\boldsymbol{g(t)}\)) известна и начальные условия в цепи нулевые.

Для вывода формулы представим непрерывную кривую входного напряжения \(\boldsymbol{u(\tau)}\) в виде суммы бесконечного числа малых ступенчатых приращений (см. Рис. 1а).

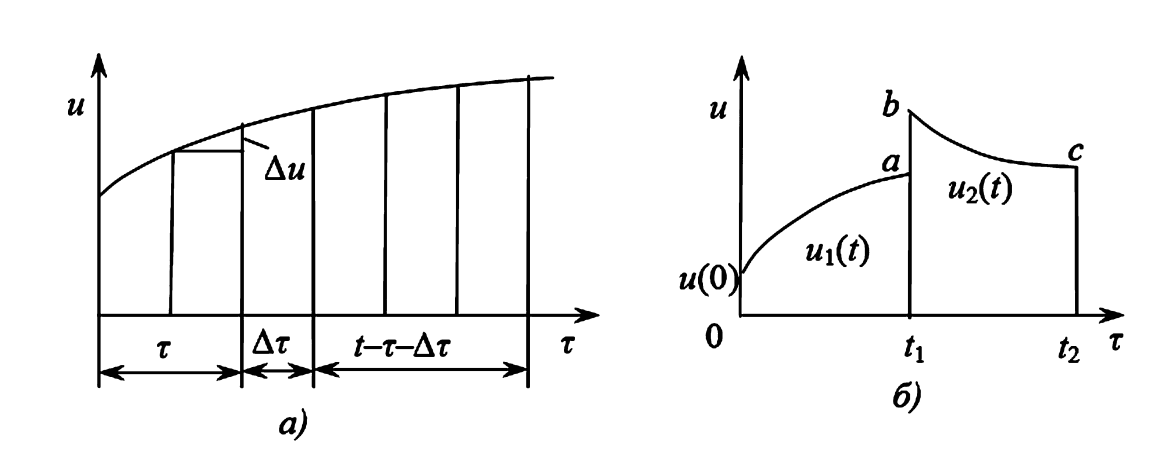
Рис. 1. Иллюстрация к выводу интеграла Дюамеля:
а) аппроксимация непрерывного напряжения \(\boldsymbol{u(\tau)}\) ступенчатой функцией;
б) напряжение, изменяющееся по сложному закону со скачками.

Ток в цепи в любой момент времени \(\boldsymbol{t}\) можно определить, используя принцип суперпозиции, как сумму токов от:

Начального значения напряжения \(\boldsymbol{u(0)}\), которое действует с момента \(\boldsymbol{t=0}\).
Всех последующих малых ступенек приращения напряжения \(\boldsymbol{\Delta u}\), каждая из которых вступает в действие с определенным запаздыванием \(\boldsymbol{\tau}\).

Каждая такая ступенька приращения напряжения \(\boldsymbol{\Delta u}\) в момент времени \(\boldsymbol{\tau}\) определяется через производную:

\(\Delta u = u'(\tau) \Delta \tau = \frac{du(\tau)}{d\tau} \Delta \tau\)

Ток от этой элементарной ступеньки в момент времени \(\boldsymbol{t}\) будет равен \(\boldsymbol{\Delta i(t) = \Delta u \cdot g(t — \tau)}\), где \(\boldsymbol{g(t — \tau)}\) — та же переходная проводимость, но сдвинутая во времени.

Суммарный ток \(\boldsymbol{i(t)}\) будет равен току от начального скачка \(\boldsymbol{u(0) \cdot g(t)}\) плюс сумма токов от всех приращений:

\(i(t) = u(0)g(t) + \sum u'(\tau)\Delta \tau \cdot g(t — \tau)\)

Заменяя конечный интервал времени \(\boldsymbol{\Delta \tau}\) на бесконечно малый дифференциал \(\boldsymbol{d\tau}\) и переходя от суммирования к интегрированию в пределах от \(\boldsymbol{0}\) до \(\boldsymbol{t}\), получаем окончательную формулу интеграла Дюамеля:

\(i(t) = u(0)g(t) + \int_{0}^{t} u'(\tau)g(t — \tau)d\tau\)

Эта формула позволяет определить переходный ток \(\boldsymbol{i(t)}\). Аналогично, для определения переходного напряжения на участке цепи, достаточно заменить переходную проводимость \(\boldsymbol{g(t)}\) на переходную функцию напряжения \(\boldsymbol{h(t)}\) (или \(\boldsymbol{k(t)}\)).

Случай разрывного (кусочно-заданного) напряжения

Если входное напряжение изменяется по более сложному закону, имея скачки (разрывы) в определенные моменты времени \(\boldsymbol{t_1}\), \(\boldsymbol{t_2}\) и т.д. (см. Рис. 1б), то ток определяют как сумму токов от всех воздействий до текущего момента времени \(\boldsymbol{t}\).

Каждый скачок напряжения \(\boldsymbol{\Delta U}\) в момент \(\boldsymbol{t_k}\) рассматривается как отдельное ступенчатое воздействие, создающее ток \(\boldsymbol{\Delta U \cdot g(t — t_k)}\).

Например, для момента времени \(\boldsymbol{t_1 < t < t_2}\) (после первого скачка \(\boldsymbol{(u_b — u_a)}\) в момент \(\boldsymbol{t_1}\)):

\(i(t) = u(0)g(t) + \int_{0}^{t_1} u’_1(\tau)g(t — \tau)d\tau + (u_b — u_a)g(t — t_1) + \int_{t_1}^{t} u’_2(\tau)g(t — \tau)d\tau\)

Для времени \(\boldsymbol{t > t_2}\) (после второго скачка \(\boldsymbol{u_c}\) в момент \(\boldsymbol{t_2}\)):

\(i(t) = u(0)g(t) + \int_{0}^{t_1} u’_1(\tau)g(t — \tau)d\tau + (u_b — u_a)g(t — t_1) + \int_{t_1}^{t_2} u’_2(\tau)g(t — \tau)d\tau + u_c g(t — t_2)\)

(Примечание: в оригинальной формуле источника \(\boldsymbol{u_c}\) может быть обозначено как \(\boldsymbol{u_c(0)}\) или \(\boldsymbol{\Delta U_c}\), что означает величину скачка в момент \(\boldsymbol{t_2}\)).

Преимущества и недостатки метода

Преимущества

Универсальность: Метод применим для входного сигнала абсолютно любой формы, которую можно описать функцией.
Наглядность: Формула имеет четкий физический смысл (сумма откликов на малые ступеньки).
Эффективность для кусочных функций: Особенно удобен для анализа цепей при воздействии кусочно-линейных или разрывных напряжений (импульсы, пилообразные сигналы).
Базируется на одной характеристике: Для полного описания отклика системы достаточно знать всего одну функцию — ее переходную характеристику \(\boldsymbol{g(t)}\) или \(\boldsymbol{h(t)}\).

Недостатки

Сложность интегрирования: В зависимости от вида функций \(\boldsymbol{u'(\tau)}\) и \(\boldsymbol{g(t)}\) вычисление итогового интеграла может быть очень трудоемким.
Нулевые начальные условия: Классическая форма интеграла Дюамеля выведена для цепей с нулевыми начальными условиями (незаряженные емкости, нулевые токи в индуктивностях). Для ненулевых условий требуются модификации формулы.
Только для линейных цепей: Метод основан на принципе суперпозиции, поэтому он неприменим для нелинейных цепей.
Требуется \(\boldsymbol{g(t)}\): Необходимо предварительно определить переходную характеристику цепи, что само по себе является отдельной задачей.

Сравнение методов анализа переходных процессов

Критерий	Интеграл Дюамеля	Классический метод	Операторный метод (преобр. Лапласа)
Основной принцип	Временной (свертка), принцип суперпозиции.	Решение диф. уравнения (поиск общего и частного решения).	Переход в ‘s-область’ (частотную), решение алгебраических уравнений.
Форма входного сигнала	Любая, особенно удобен для кусочно-заданных.	Простые формы (постоянное, синусоидальное). Для сложных — трудоемок.	Любая, имеющая изображение по Лапласу.
Начальные условия	Стандартная форма — для нулевых. Ненулевые требуют модификации.	Учитываются при поиске постоянных интегрирования.	Автоматически учитываются в операторных схемах.
Сложность	Сложность вычисления интеграла свертки.	Сложность решения диф. уравнения и поиска частного решения.	Сложность прямого и обратного преобразования Лапласа.

Пример 1. Расчет тока в RL-цепи

Задача: Определить ток в индуктивной катушке (параметры: \(\boldsymbol{R_k = 0,5 \text{ Ом}}\), \(\boldsymbol{L_k = 1 \text{ Гн}}\)) через 5 секунд после ее подключения под напряжение, изменяющееся по сложному закону (см. Рис. 1б).

Законы изменения напряжения:

\(u_1(\tau) = 150 — 100e^{-0.25\tau}\) В, действует до времени \(\boldsymbol{t_1 = 4 \text{ с}}\).
\(u_2(\tau) = 50 + 100e^{-0.4(\tau — t_1)}\) В, действует начиная с \(\boldsymbol{t_1}\) до времени \(\boldsymbol{t_2 = 6 \text{ с}}\).

Решение:

1. Определение переходной проводимости \(\boldsymbol{g(t)}\)

Определим ток \(\boldsymbol{i(t)}\) в данной RL-цепи при подключении ее под постоянное напряжение \(\boldsymbol{U = 1 \text{ В}}\). Известно, что ток в RL-цепи при \(\boldsymbol{U=1}\) равен:

\(i(t)|_{U=1} = \frac{U}{R_k}(1 — e^{-\frac{R_k}{L_k}t})\)

Следовательно, переходная проводимость:

\(g(t) = \frac{1}{R_k}(1 — e^{-\frac{R_k}{L_k}t}) = \frac{1}{0.5}(1 — e^{-\frac{0.5}{1}t}) = \boldsymbol{2(1 — e^{-0.5t})}\)

2. Определение производных напряжений

Находим производные по \(\boldsymbol{\tau}\) для каждого участка:

\(u’_1(\tau) = \frac{d}{d\tau}(150 — 100e^{-0.25\tau}) = -100 \cdot (-0.25)e^{-0.25\tau} = \boldsymbol{25e^{-0.25\tau}}\)

\(u’_2(\tau) = \frac{d}{d\tau}(50 + 100e^{-0.4(\tau — t_1)}) = 100 \cdot (-0.4)e^{-0.4(\tau — t_1)} = \boldsymbol{-40e^{-0.4(\tau — t_1)}}\)

3. Определение параметров для расчета

Расчет ведется для момента времени \(\boldsymbol{t = 5 \text{ с}}\). Этот момент находится в интервале \(\boldsymbol{t_1 < t < t_2}\) (т.к. \(\boldsymbol{4 < 5 < 6}\)). Будем использовать формулу для разрывного напряжения.

Начальное напряжение (при \(\boldsymbol{\tau=0}\)):
\(u(0) = u_1(0) = 150 — 100e^0 = 150 — 100 = \boldsymbol{50 \text{ В}}\)
Напряжение в момент скачка \(\boldsymbol{t_1 = 4}\) (конец первого участка):
\(u_a = u_1(4) = 150 — 100e^{-0.25 \cdot 4} = 150 — 100e^{-1} \approx 150 — 36.79 = \boldsymbol{113.21 \text{ В}}\)
Напряжение в момент скачка \(\boldsymbol{t_1 = 4}\) (начало второго участка):
\(u_b = u_2(4) = 50 + 100e^{-0.4(4-4)} = 50 + 100e^0 = \boldsymbol{150 \text{ В}}\)
Величина скачка напряжения в \(\boldsymbol{t_1 = 4}\):
\(\Delta U_1 = u_b — u_a = 150 — 113.21 = \boldsymbol{36.79 \text{ В}}\)

4. Расчет тока \(\boldsymbol{i(t)}\)

Ток в момент \(\boldsymbol{t=5}\) определяется по формуле:

\(i(5) = u(0)g(5) + \int_{0}^{t_1} u’_1(\tau)g(5 — \tau)d\tau + (u_b — u_a)g(5 — t_1) + \int_{t_1}^{5} u’_2(\tau)g(5 — \tau)d\tau\)

Подставляем известные функции и значения (\(\boldsymbol{t=5}\), \(\boldsymbol{t_1=4}\)):

\(i(5) = 50 \cdot g(5) + \int_{0}^{4} 25e^{-0.25\tau} \cdot g(5 — \tau)d\tau + 36.79 \cdot g(1) + \int_{4}^{5} (-40e^{-0.4(\tau — 4)}) \cdot g(5 — \tau)d\tau\)

Где \(\boldsymbol{g(t) = 2(1 — e^{-0.5t})}\). Вычисление данных определенных интегралов является трудоемкой математической задачей.

После выполнения всех подстановок и решения интегралов для момента времени \(\boldsymbol{t = 5 \text{ с}}\), итоговый ток составляет:

\(i(5) = 201.4 \text{ А}\)

Интересные факты об интеграле Дюамеля

Связь со сверткой: Интеграл Дюамеля, по своей сути, является интегралом свертки функции производной входного сигнала и переходной характеристики системы.
Импульсная характеристика: Метод тесно связан с понятием «импульсной характеристики» \(\boldsymbol{w(t)}\). Переходная характеристика \(\boldsymbol{g(t)}\) является интегралом от импульсной характеристики \(\boldsymbol{w(t)}\).
Междисциплинарность: Изначально разработанный для задач теплофизики, этот же математический аппарат используется в механике (для расчета колебаний), акустике и теории автоматического управления (ТАУ).
Основа для цифровых систем: В цифровой обработке сигналов аналогом интеграла Дюамеля является дискретная свертка, лежащая в основе работы КИХ-фильтров (FIR).
Принцип Дюамеля: Существует также «принцип Дюамеля» в решении дифференциальных уравнений в частных производных (например, волнового), который использует похожую идею сведения задачи к более простой.
Визуализация: Процесс вычисления интеграла можно представить как «скольжение» одной функции (\(\boldsymbol{g(t)}\)) в обратном времени по другой (\(\boldsymbol{u'(\tau)}\)) с вычислением площади их произведения.
Альтернативная форма: Существует и вторая, эквивалентная форма интеграла Дюамеля: \(i(t) = g(0)u(t) + \int_{0}^{t} g'(\tau)u(t — \tau)d\tau\). Выбор формы зависит от того, какую из функций (\(\boldsymbol{u(t)}\) или \(\boldsymbol{g(t)}\)) проще дифференцировать.

Часто задаваемые вопросы (FAQ)

1. Что такое интеграл Дюамеля простыми словами?

Это способ «собрать» сложную реакцию цепи из множества простых. Мы представляем сложный входной сигнал (напряжение) как серию маленьких «ступенек». Мы знаем, как цепь реагирует на одну ступеньку (это «переходная характеристика» \(\boldsymbol{g(t)}\)). Интеграл Дюамеля просто суммирует реакции на все эти маленькие ступеньки, с учетом их задержки во времени, чтобы получить итоговый ток.

2. В чем главное ограничение метода?

Метод работает только для линейных цепей (где ток пропорционален напряжению, т.е. содержащих R, L, C). Он основан на принципе суперпозиции, который в нелинейных цепях (с диодами, транзисторами) не выполняется. Также стандартная форма требует нулевых начальных условий.

3. Что такое переходная проводимость \(\boldsymbol{g(t)}\)?

Это «паспорт» реакции цепи. \(\boldsymbol{g(t)}\) — это функция, которая описывает, как изменяется ток в цепи с течением времени, если на ее вход подать простое напряжение в 1 Вольт в виде ступеньки (включить в \(\boldsymbol{t=0}\) и держать).

4. Что делать, если начальные условия не нулевые?

Метод можно модифицировать. Полный ток будет равен сумме двух составляющих: 1) тока от начальных условий (рассчитанного при \(\boldsymbol{U=0}\)) и 2) тока от входного напряжения (рассчитанного по интегралу Дюамеля, как если бы начальные условия были нулевыми).

5. Чем интеграл Дюамеля отличается от преобразования Лапласа?

Оба метода решают одну и ту же задачу, но по-разному. Интеграл Дюамеля — это метод во временной области (мы все время работаем с функциями времени \(\boldsymbol{t}\)). Метод Лапласа — это метод в частотной (операторной) области: он переводит дифференциальные уравнения во времени в алгебраические в «s-области», решает их там, а затем возвращается обратно во время. Лаплас часто проще для сложных цепей, так как не требует вычисления сложных интегралов свертки.

6. Почему в формуле используется производная напряжения \(\boldsymbol{u'(\tau)}\)?

Производная \(\boldsymbol{u'(\tau)}\) показывает «скорость» изменения напряжения. Умноженная на \(\boldsymbol{d\tau}\), она дает \(\boldsymbol{du}\) — ту самую «высоту» элементарной ступеньки, из которых мы «строим» наш сложный сигнал.

7. Применим ли этот метод для синусоидального напряжения?

Да, применим. Можно взять \(\boldsymbol{u(\tau) = U_m \sin(\omega \tau + \psi)}\), найти производную \(\boldsymbol{u'(\tau)}\) и решить интеграл. Однако для синусоидального напряжения это избыточно сложный путь. Гораздо проще использовать метод комплексных амплитуд (символический метод) или классический метод.

Заключение

Интеграл Дюамеля представляет собой мощный и теоретически элегантный метод анализа во временной области. Он незаменим для расчета отклика линейной электрической цепи на воздействия сложной, непериодической формы, которые трудно или невозможно проанализировать другими методами (например, комплексных амплитуд).

Несмотря на то, что в современной инженерной практике для сложных систем часто применяются численные методы и операторное исчисление (преобразование Лапласа), понимание принципа Дюамеля остается ключевым элементом фундаментального образования в области теории цепей, физики и теории автоматического управления, поскольку он наглядно демонстрирует связь между откликом системы и любым произвольным воздействием через принцип суперпозиции.

Нормативная база

Расчет переходных процессов и используемая терминология в электротехнике регламентируются следующими стандартами:

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий. (Устанавливает стандартизированную терминологию, включая «переходный процесс»).
ГОСТ 13109-97 — Качество электрической энергии. Нормы качества электрической энергии в системах электроснабжения общего назначения. (Регламентирует параметры качества, которые могут нарушаться при переходных процессах).

Список литературы

Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Высшая школа, 2007.
Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С. В. Основы теории цепей. — М.: Энергоатомиздат, 1989.
Демирчян К. С., Нейман Л. Р., Коровкин Н. В., Чечурин В. Л. Теоретические основы электротехники: в 3-х томах. — СПб.: Питер, 2009.