Индуктивность в цепях переменного и постоянного тока: теория и расчет

Содержание страницы

1. Физическая природа и основные определения
2. Поведение индуктивности в стационарном режиме (Постоянный ток)
3. Установившийся синусоидальный режим: Индуктивное сопротивление и сдвиг фаз
4. Реальная катушка индуктивности: Схема замещения
5. Добротность индуктивности (Quality Factor)
6. Практический расчет индуктивности: Методика и Пример
7. Сравнительная таблица базовых пассивных элементов
8. Интересные факты об индуктивности
9. FAQ: Часто задаваемые вопросы (Expert Edition)
Заключение

Индуктивность — это фундаментальное свойство электрической цепи, характеризующее её способность накапливать энергию в магнитном поле при протекании электрического тока, а также сопротивляться изменению силы этого тока. В качестве физического компонента индуктивность (или катушка индуктивности, соленоид, дроссель) представляет собой пассивный двухполюсник.

С исторической точки зрения, явление электромагнитной индукции было независимо открыто Майклом Фарадеем в Англии (1831 г.) и Джозефом Генри в США (1832 г.). Именно в честь Джозефа Генри названа единица измерения индуктивности в системе СИ — Генри (Гн). Это открытие стало поворотным моментом в истории электротехники, позволив человечеству перейти от гальванических элементов к генераторам и трансформаторам, сформировав основу современной энергетики.

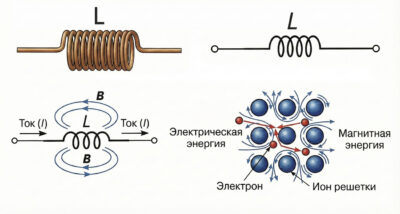
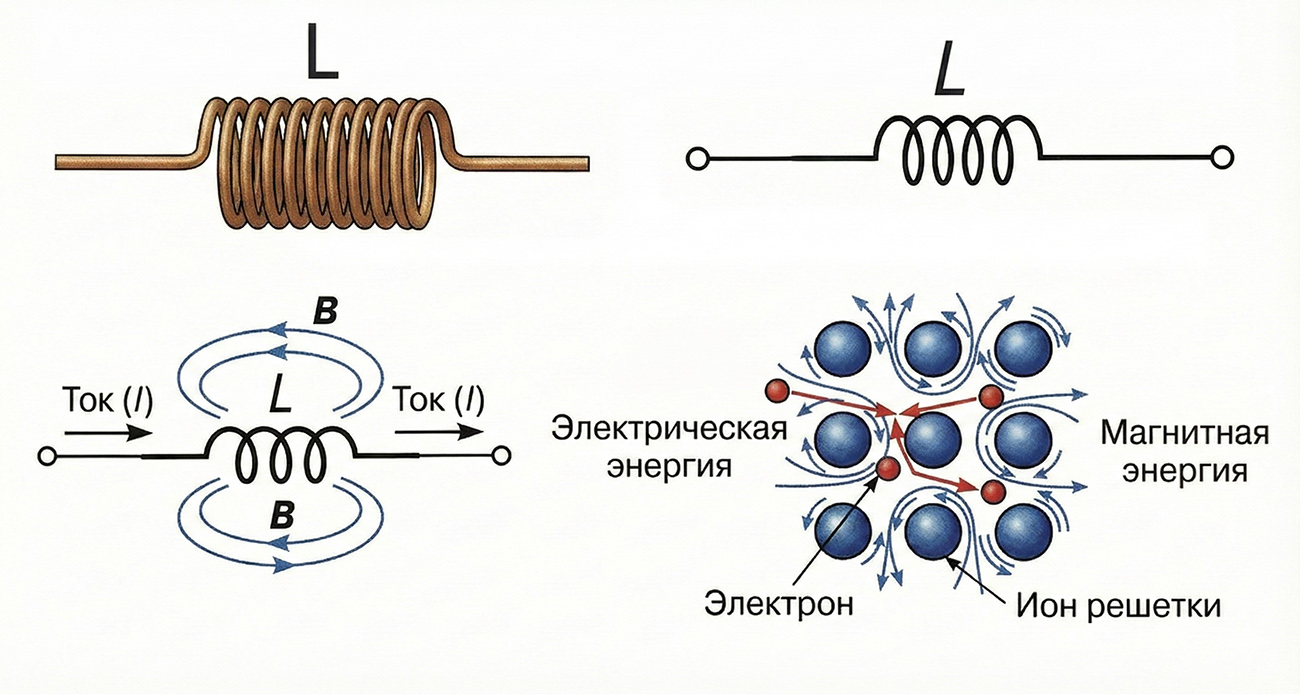
Замечание: Важно различать понятие «индуктивность» как параметр (величина \(L\)) и «индуктивность» как элемент цепи (катушка). Идеальная индуктивность является консервативным элементом: она не рассеивает энергию в тепло (как резистор), а лишь запасает её и возвращает обратно в цепь.

На этой иллюстрации представлена инфографика, объясняющая понятие индуктивности (L). В верхней части изображения показан внешний вид реальной катушки (соленоида) и соответствующее ей условное обозначение на электрических схемах. В нижней левой части демонстрируется физический принцип работы: протекающий через катушку электрический ток (I) генерирует магнитное поле (B), показанное замкнутыми линиями. Справа внизу приведена схема на микроскопическом уровне, где изображено движение электронов через кристаллическую решетку ионов, иллюстрирующая взаимосвязь электрической и магнитной энергий в проводнике.
Ток (I): Когда электрический ток протекает через провод, он всегда создает вокруг себя магнитное поле.
Эффект катушки: Если провод прямой, поле вокруг него слабое и «размазанное». Но когда мы скручиваем провод в спираль (как на рисунке), магнитные поля от каждого отдельного витка складываются внутри катушки.
Магнитное поле (B): Синие линии показывают концентрацию этого поля. Катушка работает как магнитная «линза», фокусируя поле внутри себя.
Смысл индуктивности (L): Индуктивность — это мера того, насколько сильно эта конкретная катушка может «запасать» энергию в виде этого магнитного поля.

1. Физическая природа и основные определения

Индуктивность (см. Рис. 1) — это идеализированный элемент схемы, который моделирует эффект создания магнитного потока током. Ключевым свойством этого элемента является инерционность: ток в катушке не может измениться мгновенно. Это обусловлено явлением самоиндукции: при любом изменении тока возникает ЭДС, препятствующая этому изменению (Правило Ленца).

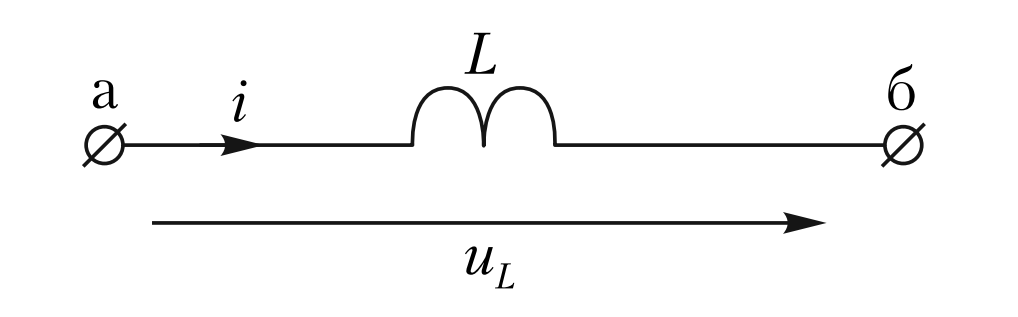
Рис. 1. Индуктивность — элемент, запасающий энергию в магнитном поле. Стрелками показаны выбранные положительные направления тока \(i\) и напряжения \(u_L\).

При выбранных на Рис. 1 положительных направлениях (когда стрелки тока и напряжения совпадают по направлению, что соответствует пассивной системе знаков), мгновенное значение напряжения на зажимах индуктивности \(u_L\) определяется разностью потенциалов между точками входа и выхода (\(\phi_а – \phi_б\)) и фундаментальным дифференциальным соотношением:

u_L = L \frac{di}{dt}

Это уравнение гласит: разность потенциалов на индуктивном элементе прямо пропорциональна скорости изменения тока во времени.

Здесь величина \(L\) выступает как коэффициент пропорциональности. Если \(L = \text{const}\), то есть величина индуктивности не зависит от величины протекающего через нее тока, такую индуктивность называют линейной. В противном случае (например, при наличии ферромагнитного сердечника, входящего в насыщение), элемент становится нелинейным, и анализ цепи значительно усложняется.

Аналогия из механики: Индуктивность в электричестве — это полный аналог массы в механике.

Масса препятствует изменению скорости тела (инерция). Чтобы разогнать тяжелый маховик (увеличить скорость), нужно приложить силу. Чтобы остановить его — тоже нужна сила.
Индуктивность препятствует изменению тока. Чтобы увеличить ток («разогнать» заряды), нужно приложить напряжение. Чтобы резко прервать ток — индуктивность выбросит накопленную энергию в виде скачка напряжения (ЭДС самоиндукции).

Энергия магнитного поля

Так как идеальная индуктивность не потребляет энергию безвозвратно, она работает как накопитель. Энергия \(W_M\), запасенная в магнитном поле линейной катушки к моменту времени \(t\), определяется интегралом мощности:

W_M = \int_0^t u_L \cdot i \, dt = \int_0^i L \frac{di}{dt} \cdot i \, dt = \int_0^i L i \, di = \frac{L i^2}{2}

Эта формула \(W_M = \frac{L i^2}{2}\) подтверждает, что запасенная энергия при соответствующих условиях (например, при убывании тока до нуля) может быть полностью возвращена источнику или передана другим элементам цепи.

2. Поведение индуктивности в стационарном режиме (Постоянный ток)

Рассмотрим поведение идеальной катушки в цепях постоянного тока (DC). Стационарный режим подразумевает, что все переходные процессы завершены, и токи с напряжениями неизменны во времени.

Исходя из основной формулы \( u_L = L \frac{di}{dt} \), проанализируем ситуацию:

Если ток \( i(t) = \text{const} \) (константа), то его производная по времени равна нулю:

\frac{di}{dt} = 0 \quad \Rightarrow \quad u_L = L \cdot 0 = 0

Разность потенциалов на индуктивности возникает только в случае изменения тока во времени. Следовательно, в стационарном режиме под действием постоянных источников индуктивность ведет себя как обычный проводник с нулевым сопротивлением.

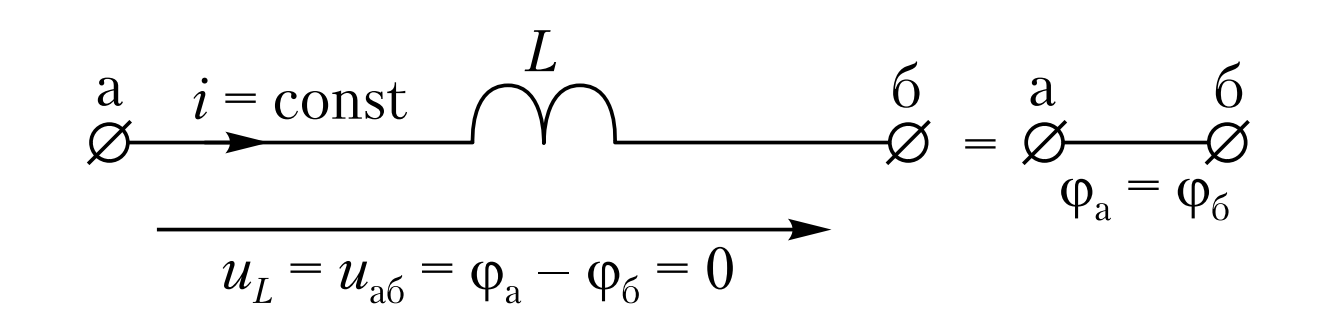
Рис. 2. В стационарном режиме (\(i = \text{const}\)) индуктивность проявляет себя как короткозамкнутая перемычка (идеальный проводник).

В практике такую перемычку называют «короткое замыкание» (к.з.). На схеме замещения (Рис. 2) индуктивность заменяется проводом. Это означает, что для постоянного тока катушка «прозрачна» (если пренебречь омическим сопротивлением провода, о чем будет сказано ниже в разделе о реальных катушках).

3. Установившийся синусоидальный режим: Индуктивное сопротивление и сдвиг фаз

Наибольший интерес представляет поведение индуктивности в цепях переменного тока (AC). Пусть через индуктивность протекает синусоидальный ток:

i(t) = I_m \sin(\omega t)

Где:

\(I_m\) — амплитуда тока,

\(\omega = 2\pi f\) — угловая частота.

Найдем напряжение на индуктивности, используя операцию дифференцирования:

u_L(t) = L \frac{d}{dt} (I_m \sin(\omega t)) = L \cdot I_m \cdot \frac{d}{dt}(\sin(\omega t))

u_L(t) = L \cdot I_m \cdot \omega \cos(\omega t) = \omega L I_m \cos(\omega t)

Для удобства сравнения фаз приведем функцию косинуса к синусу, используя тригонометрическое тождество \(\cos(\alpha) = \sin(\alpha + 90^\circ)\):

u_L(t) = \omega L I_m \sin(\omega t + 90^\circ) = U_{mL} \sin(\omega t + 90^\circ)

Анализ полученного результата

Вывод 1: Форма сигнала. Напряжение на индуктивности остается гармонической функцией той же частоты \(\omega\), что и ток. Индуктивность является линейным элементом и не вносит частотных искажений (не генерирует новых гармоник).

Вывод 2: Фазовый сдвиг. Фаза синусоидального напряжения на индуктивности превышает фазу тока ровно на \(90^\circ\) (\(\pi/2\) радиан). Это означает, что напряжение «опережает» ток. На временно́й диаграмме (Рис. 3, а) кривая напряжения проходит через ноль и достигает максимума на четверть периода раньше, чем кривая тока.

Вывод 3: Закон Ома для индуктивности. Связь амплитуд напряжения и тока описывается соотношением:

U_{mL} = \omega L I_m

Это соотношение структурно идентично закону Ома \(U = I \cdot R\), где роль сопротивления выполняет величина:

X_L = \omega L = 2\pi f L

Величина \(X_L\) называется индуктивным сопротивлением (реактивным сопротивлением индуктивности) и измеряется в Омах.

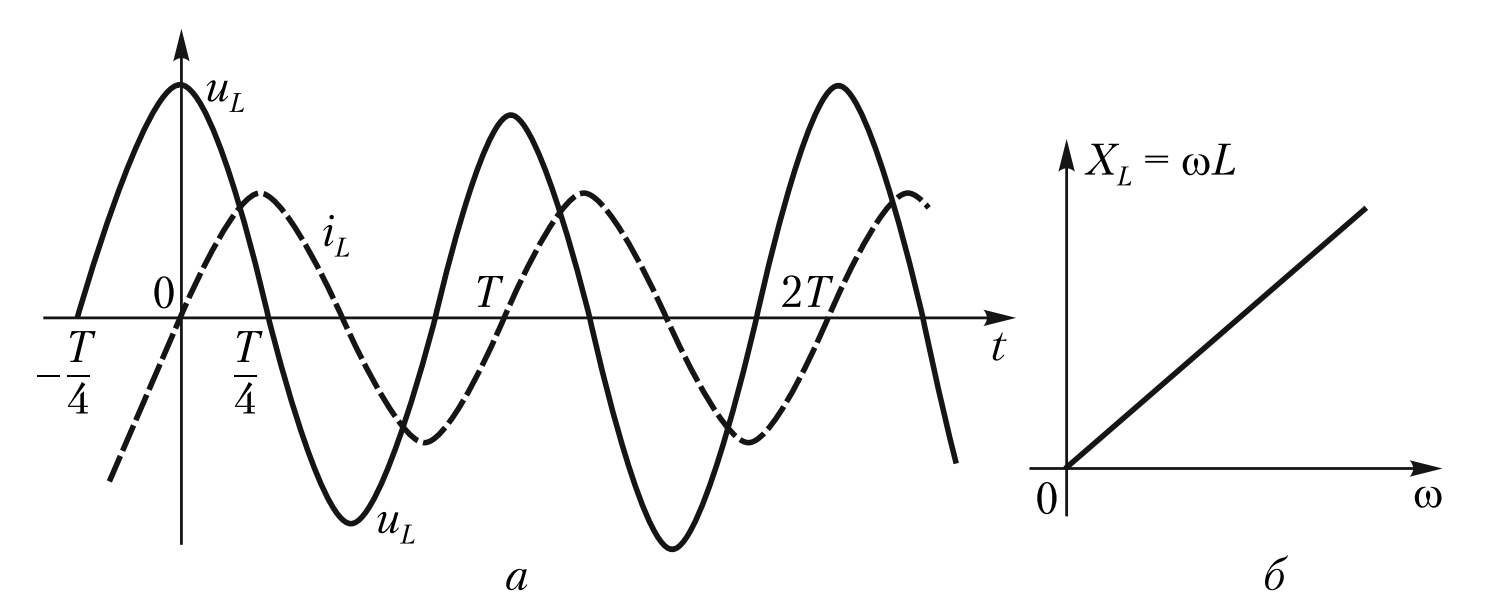
Рис. 3. Синусоидальный режим в индуктивности:

а — Временные диаграммы: напряжение \(u_L\) опережает ток \(i\) по фазе на \(90^\circ\).
б — Частотная характеристика: индуктивное сопротивление \(X_L = \omega L\) линейно зависит от частоты \(\omega\).

Частотные свойства (Фильтрация)

Как видно из графика на Рис. 3 (б), индуктивное сопротивление прямо пропорционально частоте:

При низких частотах (\(\omega \to 0\)), \(X_L \to 0\). Индуктивность почти не оказывает сопротивления току (стремится к короткому замыканию).
При высоких частотах (\(\omega \to \infty\)), \(X_L \to \infty\). Индуктивность представляет собой огромное сопротивление, практически разрыв цепи.

В инженерной практике это свойство используется для фильтрации: катушки индуктивности (дроссели) свободно пропускают постоянный и низкочастотный ток, но блокируют высокочастотные помехи и сигналы. Поэтому при качественном анализе схем:

На частоте \(\omega \approx 0\) — индуктивность заменяют закороткой.
На частоте \(\omega \to \infty\) — индуктивность заменяют разрывом (холостой ход).

4. Реальная катушка индуктивности: Схема замещения

До сих пор мы рассматривали идеальную индуктивность. Однако любой физический объект обладает потерями и паразитными параметрами. Реальная катушка представляет собой провод, намотанный на каркас, и имеет следующие несовершенства:

Активное сопротивление провода: Медь или алюминий, из которых сделана обмотка, имеют конечное сопротивление \(R\).
Потери в сердечнике (если есть): Вихревые токи и гистерезис в магнитном материале приводят к нагреву.
Межвитковая емкость: Между витками существует паразитная емкость, которая начинает влиять на работу на высоких частотах (возникает резонанс).

Для расчетов на низких и средних частотах (когда емкостью можно пренебречь) простейшая схема замещения реальной катушки содержит два сосредоточенных элемента: идеальную индуктивность \(L_Э\) и резистор \(R_Э\), отражающий все тепловые потери (Рис. 4).

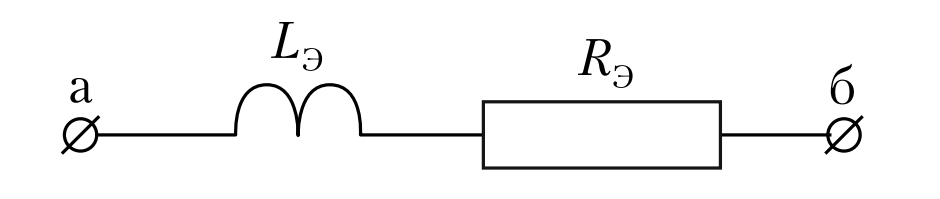
Рис. 4. Простейшая последовательная схема замещения реальной катушки индуктивности, состоящая из эквивалентного резистора \(R_Э\) и индуктивности \(L_Э\).

В этой схеме ток через элементы протекает один и тот же, а общее напряжение складывается из падения напряжения на активном сопротивлении (в фазе с током) и на индуктивности (опережает ток на 90 градусов).

5. Добротность индуктивности (Quality Factor)

Качество реальной катушки индуктивности оценивается тем, насколько она близка к идеальной (чисто реактивной). Для количественной характеристики соотношения между полезным (индуктивным \(X_L = \omega L_Э\)) и вредным (резистивным \(R_Э\)) сопротивлениями вводится понятие добротности (\(Q\)-фактор).

Q_L = \frac{X_L}{R_Э} = \frac{\omega L_Э}{R_Э}

Также добротность можно определить через энергетические понятия:

Q_L = 2\pi \cdot \frac{\text{Энергия, запасенная в поле}}{\text{Энергия, потерянная за период}}

Характеристики добротности:

Это безразмерная величина.
Она зависит от частоты (так как в числителе стоит \(\omega\), а \(R_Э\) также может зависеть от частоты из-за скин-эффекта).
Чем выше \(Q\), тем «чище» индуктивность, тем меньше потери и тем уже полоса пропускания в резонансных контурах (выше избирательность).

Для применяемых в современной инженерной практике высокодобротных катушек в радиочастотном диапазоне (например, на частотах порядка \(10 \cdot 10^6\) Гц или 10 МГц) добротность может достигать значений от 50 до нескольких сотен (Q = 100…300). В СВЧ диапазоне применяются специальные объемные резонаторы, где добротность достигает тысяч.

6. Практический расчет индуктивности: Методика и Пример

В инженерной практике часто возникает задача: спроектировать катушку (дроссель) с заданным значением \(L\) или определить индуктивность уже существующей обмотки.

Наиболее распространенной конструкцией является соленоид — длинная цилиндрическая катушка. Для неё справедлива классическая формула расчета индуктивности, связывающая геометрические размеры и магнитные свойства среды.

Базовая формула расчета для однослойного соленоида

Для длинного соленоида (где длина намотки \(l\) значительно превышает диаметр \(D\)) индуктивность определяется следующим соотношением:

L = \frac{\mu_0 \cdot \mu_r \cdot N^2 \cdot S}{l}

Где параметры имеют следующий физический смысл:

\( L \) — индуктивность (Генри, Гн);
\( \mu_0 \) — магнитная постоянная (вакуумная проницаемость), фундаментальная физическая константа:
\( \mu_0 = 4\pi \cdot 10^{-7} \approx 1.257 \cdot 10^{-6} \) Гн/м;
\( \mu_r \) — относительная магнитная проницаемость материала сердечника (безразмерная величина). Для воздуха \( \mu_r \approx 1 \), для ферритов может достигать 600–10000;
\( N \) — количество витков провода (обратите внимание, зависимость квадратичная: увеличение витков в 2 раза повышает индуктивность в 4 раза!);
\( S \) — площадь поперечного сечения катушки (м²). Для круглой формы \( S = \pi r^2 = \frac{\pi D^2}{4} \);
\( l \) — длина намотки (м).

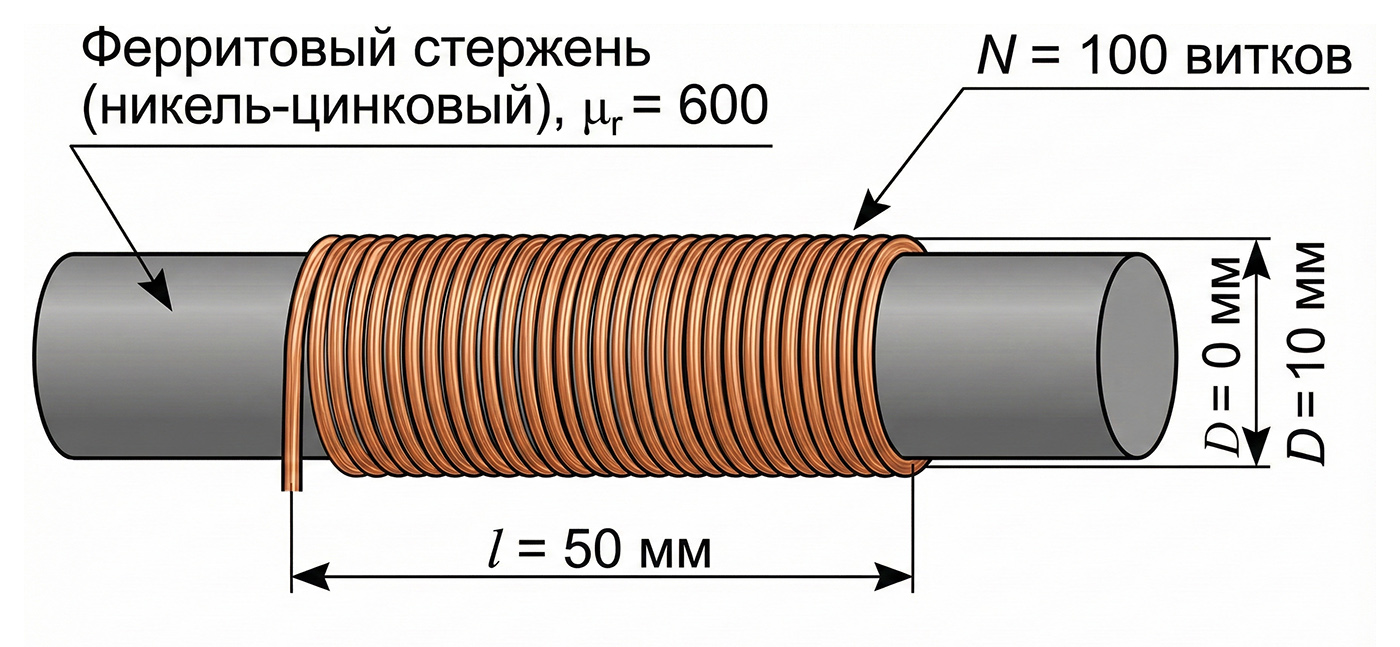
Рис. 7. Конструктивный чертеж дросселя на ферритовом стержне. На схеме четко обозначены зоны измерения: длина намотки \(l\) составляет 50 мм, диаметр сердечника \(D\) равен 10 мм. Обмотка содержит 100 витков провода, уложенных виток к витку.

Пример инженерного расчета

Рассмотрим практическую задачу. Необходимо изготовить помехоподавляющий дроссель на ферритовом стержне.

Дано:

Материал сердечника: никель-цинковый феррит с \( \mu_r = 600 \).
Диаметр сердечника (\(D\)): 10 мм = \( 0.01 \) м.
Длина намотки (\(l\)): 50 мм = \( 0.05 \) м.
Количество витков (\(N\)): 100 витков.

Решение:

1. Сначала вычислим площадь поперечного сечения сердечника \(S\):

S = \frac{\pi \cdot D^2}{4} = \frac{3.14159 \cdot (0.01)^2}{4} \approx 7.854 \cdot 10^{-5} \, \text{м}^2

2. Рассчитаем абсолютную магнитную проницаемость сердечника \( \mu_a = \mu_0 \cdot \mu_r \):

\mu_a = (4\pi \cdot 10^{-7}) \cdot 600 \approx 7.54 \cdot 10^{-4} \, \text{Гн/м}

3. Подставим значения в основную формулу:

L = \frac{7.54 \cdot 10^{-4} \cdot (100)^2 \cdot 7.854 \cdot 10^{-5}}{0.05}

4. Проводим вычисления:

L = \frac{7.54 \cdot 10^{-4} \cdot 10^4 \cdot 7.854 \cdot 10^{-5}}{0.05} = \frac{7.54 \cdot 7.854 \cdot 10^{-1}}{0.05}

L \approx \frac{5.922 \cdot 10^{-1}}{0.05} = \frac{0.5922}{0.05} \approx 11.84 \, \text{мГн}

Ответ: Расчетная индуктивность дросселя составляет приблизительно 11.84 мГн (миллигенри).

Корректировка для коротких катушек (Коэффициент Нагаоки):

Приведенная выше формула идеально работает только для очень длинных соленоидов (\(l \gg D\)). В реальности, если длина катушки сопоставима с её диаметром, магнитное поле на краях ослабевает («эффект краевых полей»).

Для точного расчета вводится поправочный коэффициент Нагаоки \(K\) (0 < K < 1), зависящий от отношения \(D/l\):

\( L_{\text{real}} = K \cdot L_{\text{theor}} \)

Например, если длина равна диаметру (\(l=D\)), коэффициент \(K \approx 0.69\), то есть реальная индуктивность будет на 30% меньше расчетной по простой формуле.

Важно о насыщении!
При расчете катушек с ферромагнитным сердечником нельзя забывать про ток насыщения. Формула предполагает, что \( \mu_r \) — константа. Однако при превышении определенного тока магнитный материал входит в насыщение, \( \mu_r \) резко падает (стремится к 1), и индуктивность катастрофически снижается. Это приводит к резкому росту тока и выходу схемы из строя.

7. Сравнительная таблица базовых пассивных элементов

Для лучшего понимания места индуктивности в теории цепей, сравним её с другими базовыми элементами.

Характеристика	Резистор (R)	Индуктивность (L)	Конденсатор (C)
Основное свойство	Ограничивает ток, рассеивает энергию	Препятствует изменению тока, запасает магн. энергию	Препятствует изменению напряжения, запасает эл. энергию
Связь u и i	\(u = i \cdot R\)	\(u = L \cdot \frac{di}{dt}\)	\(i = C \cdot \frac{du}{dt}\)
Сопротивление (AC)	\(R\) (не зависит от \(f\))	\(X_L = \omega L\) (растет с \(f\))	\(X_C = \frac{1}{\omega C}\) (падает с \(f\))
Фазовый сдвиг	0° (в фазе)	Напряжение опережает ток на 90°	Ток опережает напряжение на 90°
Поведение на DC (\(\omega=0\))	Сопротивление R	Короткое замыкание	Разрыв цепи

8. Интересные факты об индуктивности

Историческая несправедливость.
Хотя единицу измерения назвали в честь американца Джозефа Генри, первым явление электромагнитной индукции открыл Майкл Фарадей в 1831 году. Генри сделал это открытие почти одновременно (в 1832 году), но замешкался с публикацией результатов. В науке, как и в спорте, важна не только скорость открытия, но и скорость фиксации результата.
Энергия в МРТ.
В аппаратах магнитно-резонансной томографии (МРТ) используются сверхпроводящие катушки индуктивности. Однажды «закачанный» в такую катушку ток может циркулировать годами без источника питания, создавая колоссальное магнитное поле. Энергия, запасенная в поле типичного томографа (\( W = Li^2/2 \)), сопоставима с кинетической энергией груженого грузовика на скорости 100 км/ч.
Паразит на высоких частотах.
Любой проводник имеет индуктивность, даже прямой кусок проволоки (примерно 1 нГн на 1 мм длины). В современных процессорах, работающих на частотах в миллиарды герц (ГГц), даже ножка микросхемы становится серьезным индуктивным сопротивлением \( X_L = \omega L \), которое может исказить сигнал. Поэтому инженеры стараются делать соединения максимально короткими.
Рельсотрон (Railgun).
Грозное оружие будущего — рельсовая пушка — работает исключительно на законах индуктивности. Огромный ток создает мощнейшее магнитное поле, которое с силой Лоренца выталкивает снаряд. Здесь индуктивность выступает не как элемент защиты, а как способ мгновенного преобразования электрической энергии в кинетическую.
Беспроводная магия.
Зарядка вашего смартфона без проводов (стандарт Qi) основана на принципе взаимной индукции. Катушка в зарядной станции и катушка в телефоне образуют воздушный трансформатор. Эффективность передачи энергии достигается за счет точного резонанса: \( \omega L = 1/(\omega C) \), что позволяет передавать энергию «сквозь воздух» с КПД до 80%.

9. FAQ: Часто задаваемые вопросы (Expert Edition)

В1: Почему при выдергивании вилки мощного прибора из розетки видна искра?

Это проявление ЭДС самоиндукции. Как мы выяснили из теории, ток в индуктивности (обмотке мотора пылесоса или трансформатора) не может исчезнуть мгновенно. При резком разрыве цепи (\( dt \to 0 \)) производная \( di/dt \) стремится к бесконечности.

Индуктивность реагирует выбросом напряжения \( u_L = -L \frac{di}{dt} \), которое может достигать тысяч вольт. Это напряжение пробивает воздушный промежуток между контактами вилки и розетки, создавая плазменный шнур — искру или дугу, поддерживающую протекание тока еще какое-то время.

В2: В чем отличие «Дросселя» от «Катушки индуктивности»?

Технически это один и тот же элемент, разница лишь в назначении:

Катушка индуктивности — общий термин. Обычно так называют элементы колебательных контуров, где важна точность частоты и высокая добротность \( Q \).
Дроссель (от нем. drosseln — ограничивать, глушить) — это катушка, предназначенная для подавления (фильтрации) переменной составляющей тока или высокочастотных помех. Дроссели стоят в блоках питания для сглаживания пульсаций.

В3: Что такое насыщение сердечника и почему это опасно?

Ферромагнитные сердечники (железо, феррит) могут усиливать магнитное поле только до определенного предела. Магнитные домены в материале выстраиваются вдоль поля, и когда они все «повернулись», материал насыщается.

В этот момент относительная магнитная проницаемость \( \mu_r \) резко падает (с тысяч единиц практически до 1). Согласно формуле \( L \sim \mu_r \), индуктивность катушки мгновенно уменьшается в сотни раз. Катушка превращается в простой кусок провода, ток лавинообразно нарастает, что обычно приводит к взрыву силовых ключей или перегоранию предохранителей.

В4: Можно ли измерить индуктивность обычным мультиметром?

В большинстве случаев — нет. Стандартный мультиметр в режиме «прозвонки» или измерения сопротивления покажет только активное сопротивление провода \( R_{DC} \) (Омы). Это позволит понять, не оборван ли провод, но не скажет ничего об индуктивности \( L \).

Для измерения \( L \) нужен специальный RLC-метр или мультиметр с функцией измерения индуктивности. Такие приборы подают на катушку переменный ток тестовой частоты и вычисляют индуктивность по фазовому сдвигу и импедансу.

В5: Почему сердечники трансформаторов делают из пластин, а не из цельного куска металла?

Это делается для борьбы с вихревыми токами (токами Фуко). Переменное магнитное поле наводит ЭДС не только в обмотке, но и в самом электропроводящем сердечнике. Если сердечник сплошной, в нем возникают мощные замкнутые токи, которые раскаляют железо докрасна, вызывая огромные потери энергии.

Наборная конструкция из тонких изолированных пластин (шихтованный сердечник) разрывает пути для этих токов, резко снижая потери и нагрев. В высокочастотных дросселях вместо пластин используют ферриты — специальную магнитокерамику, которая вообще не проводит электрический ток.

Заключение

Индуктивность является одним из трех китов электротехники (наряду с емкостью и сопротивлением). Понимание её работы в стационарном режиме (как проводник) и в синусоидальном режиме (как частотно-зависимое сопротивление с фазовым сдвигом) необходимо любому инженеру. Реальные катушки всегда имеют активные потери, характеризуемые добротностью \(Q\). Учет этих свойств позволяет создавать эффективные фильтры, трансформаторы, моторы и системы передачи энергии.

Нормативная база

ГОСТ 2.723-68 — Единая система конструкторской документации. Обозначения условные графические в схемах. Катушки индуктивности, дроссели, трансформаторы, автотрансформаторы и магнитные усилители.
ГОСТ IEC 60050-151-2014 — Международный электротехнический словарь. Часть 131. Теория электрических и магнитных цепей (определяет термины «индуктивность», «взаимная индуктивность»).
ГОСТ 20718-75 — Катушки индуктивности аппаратуры связи. Термины и определения.

Индуктивность в электрической цепи: устройство, теория, расчет и физика процессов