Емкость в электрической цепи: Теория, устройство, расчет и принцип действия

Содержание страницы

1. Идеальная емкость: Физический смысл и математическая модель
2. Стационарный режим (Постоянный ток)
3. Установившийся синусоидальный режим (Переменный ток)
4. Реальная емкость: Схемы замещения и потери
5. Практический пример: Расчет реактивного сопротивления и тока конденсатора
6. Сравнительный анализ и применение
7. Интересные факты о емкости и конденсаторах
8. Часто задаваемые вопросы (FAQ)
Заключение

Электрическая емкость — это физическая величина, характеризующая способность проводника или системы проводников накапливать электрический заряд. В контексте теории электрических цепей, под емкостью понимают пассивный элемент схемы (конденсатор), который способен запасать энергию в своем электрическом поле и, в идеальном случае, не рассеивать ее в виде тепла.

Историческая справка: История конденсатора начинается с середины XVIII века. В 1745 году голландский физик Питер ван Мушенбрук (и независимо от него немец Эвальд Юрген фон Клейст) создал «Лейденскую банку» — первый в мире конденсатор. Это устройство позволяло накапливать заряд статического электричества. Позже, великий Майкл Фарадей ввел понятие диэлектрической проницаемости и заложил основы теории поля. Именно в его честь названа единица измерения емкости в системе СИ — Фарад (Ф).

Данный материал представляет собой подробное техническое руководство. Мы разберем физику процессов, математический аппарат, поведение емкости на постоянном и переменном токе, а также учтем паразитные параметры реальных компонентов.

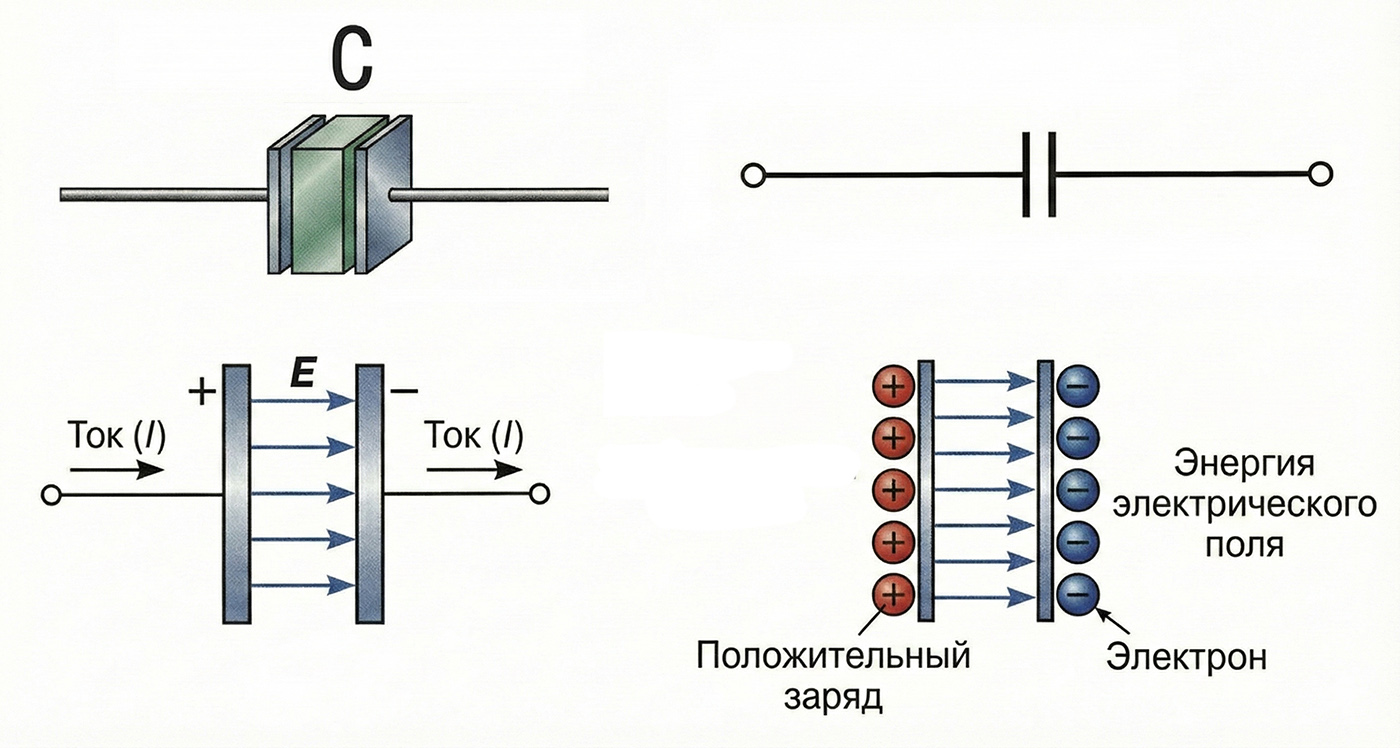
Когда к выводам прикладывается внешнее напряжение, электрический ток (I) приносит положительные заряды на левую обкладку и отводит их с правой (накапливая там электроны). Поскольку между пластинами находится диэлектрик, носители заряда не могут перетечь напрямую (цепь гальванически развязана).

Вместо протекания сквозного тока, между разноименно заряженными пластинами возникает электрическое поле (E). Именно это поле удерживает заряды на пластинах за счет сил кулоновского притяжения и является хранилищем потенциальной энергии конденсатора. Процесс накопления продолжается до тех пор, пока напряжение внутреннего поля конденсатора не уравновесит внешнее приложенное напряжение.

1. Идеальная емкость: Физический смысл и математическая модель

В теории цепей мы часто оперируем понятием идеальной емкости. Это абстракция, математическая модель, которая обладает исключительно свойством накапливать заряд, игнорируя утечки тока через изоляцию или сопротивление выводов.

В основе работы элемента лежит принцип разделения зарядов. Когда к двум изолированным друг от друга проводникам (обкладкам) прикладывается напряжение, на них скапливаются разноименные заряды \( +q \) и \( -q \). Электрическое поле, возникающее между обкладками, является носителем энергии.

Аналогия с гидродинамикой: Представьте трубу, перекрытую упругой резиновой мембраной. Вода (ток) не может протекать сквозь мембрану, но может растягивать ее. Чем сильнее напор воды (напряжение), тем сильнее растягивается мембрана, накапливая потенциальную энергию. Если напор убрать, мембрана вернется в исходное состояние, выталкивая воду обратно. Так работает и конденсатор: ток не течет «сквозь» диэлектрик, но смещение зарядов создает ток во внешней цепи при зарядке и разрядке.

1.1. Основные дифференциальные и интегральные соотношения

Рассмотрим схематическое изображение емкостного элемента. Обратите внимание на направления тока и напряжения.

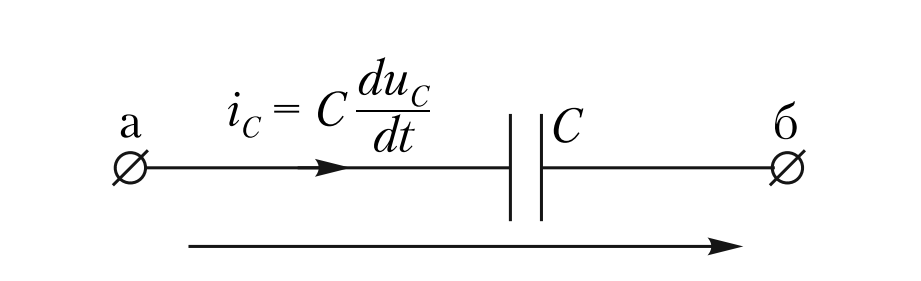
Рисунок 1. Емкость — элемент, запасающий энергию в электрическом поле. Положительные направления тока \( i_C \) и напряжения \( u_C \) выбраны согласованными (совпадающими). Ток в ветви с емкостью существует только при изменении напряжения во времени.

Фундаментальное определение емкости связывает заряд \( q \) и напряжение \( u_C \):

q(t) = C \cdot u_C(t)

Так как электрический ток \( i(t) \) — это скорость изменения заряда во времени (\( i = dq/dt \)), мы можем получить выражение для тока, продифференцировав уравнение заряда. Для линейного элемента, где величина емкости \( C = \text{const} \) и не зависит от напряжения или времени:

i_C(t) = \frac{d(Cu_C)}{dt} = C \frac{du_C(t)}{dt}

Это уравнение является ключевым для понимания динамики. Из него следует важнейший вывод: ток через конденсатор пропорционален скорости изменения напряжения. Если напряжение не меняется (\( du_C/dt = 0 \)), ток равен нулю.

Для нахождения напряжения при известном токе необходимо выполнить обратную операцию — интегрирование:

u_C(t) = \frac{1}{C} \int_{-\infty}^{t} i_C(\tau) d\tau = u_C(0) + \frac{1}{C} \int_{0}^{t} i_C(\tau) d\tau

Здесь слагаемое \( u_C(0) \) отражает «память» конденсатора — напряжение, которое было на нем к моменту начала наблюдения (начальное условие). Это подтверждает тезис о том, что конденсатор является энергонезависимым (в пределах времени удержания заряда) хранилищем энергии.

Важно: Напряжение на емкости не может измениться скачком. Для мгновенного изменения напряжения \( u_C \) потребовался бы ток бесконечной величины (\( i_C \to \infty \)), что физически невозможно в реальных цепях ограниченной мощности. Это свойство называется законом коммутации для емкости.

2. Стационарный режим (Постоянный ток)

Рассмотрим поведение емкости под действием источников постоянного напряжения (DC). Этот режим называется установившимся стационарным режимом. В данном случае все переходные процессы завершены, и электрические величины (токи, напряжения) не изменяются во времени.

Исходя из формулы тока, полученной нами ранее:

i_C = C \frac{du_C}{dt}

Поскольку в стационарном режиме напряжение постоянно (\( u_C = \text{const} \)), его производная по времени равна нулю:
\( \frac{du_C}{dt} = 0 \). Следовательно:

i_C = C \cdot 0 = 0

Это означает, что постоянный ток через конденсатор не протекает. Диэлектрик между обкладками является изолятором.

Рисунок 2. В стационарном режиме при \( u_C = \text{const} \) идеальная емкость проявляет себя как разрыв цепи (обрыв ветви). Ток \( i_C = 0 \).

На эквивалентных схемах для расчета режима по постоянному току ветвь с конденсатором можно мысленно удалить (разорвать). При этом напряжение на зажимах обрыва может быть отличным от нуля и равняться разности потенциалов между точками подключения.

3. Установившийся синусоидальный режим (Переменный ток)

Наибольший интерес для электротехники представляет поведение емкости в цепях переменного синусоидального тока (AC), так как именно так передается энергия в промышленных сетях и работают сигнальные цепи.

Пусть к обкладкам конденсатора емкостью \( C \) приложено напряжение, изменяющееся по гармоническому закону:

u_C(t) = U_{mC} \sin(\omega t)

где:

\( U_{mC} \) — амплитуда напряжения (Вольт);
\( \omega = 2\pi f \) — угловая частота (рад/с);
\( t \) — время (с).

Найдем ток, протекающий через емкость, используя операцию дифференцирования:

i_C(t) = C \frac{d(U_{mC} \sin \omega t)}{dt} = C \cdot U_{mC} \cdot \frac{d(\sin \omega t)}{dt}

Производная синуса дает косинус, умноженный на внутреннюю производную аргумента (\( \omega \)):

i_C(t) = \omega C U_{mC} \cos(\omega t)

Для удобства сравнения фаз тока и напряжения, приведем функцию косинуса к синусу, используя тригонометрическую формулу приведения \( \cos(\alpha) = \sin(\alpha + 90^\circ) \):

i_C(t) = I_m \sin(\omega t + 90^\circ)

где амплитуда тока равна \( I_m = \omega C U_{mC} \).

3.1. Фазовые соотношения

Анализируя полученные выражения для \( u_C(t) \) и \( i_C(t) \), мы приходим к фундаментальному выводу:

Вывод: В синусоидальном режиме напряжение и ток в емкости представляют собой гармоники одной частоты, но они сдвинуты по фазе. Ток опережает напряжение на угол \( \pi/2 \) (или 90°).

Физически это объясняется тем, что для появления напряжения на обкладках (накопления энергии) сначала должен протечь ток (прийти заряд). Ток максимален в моменты, когда напряжение переходит через ноль (максимальная скорость изменения потенциала), и равен нулю, когда напряжение достигает пика (момент остановки накопления заряда перед разрядом).

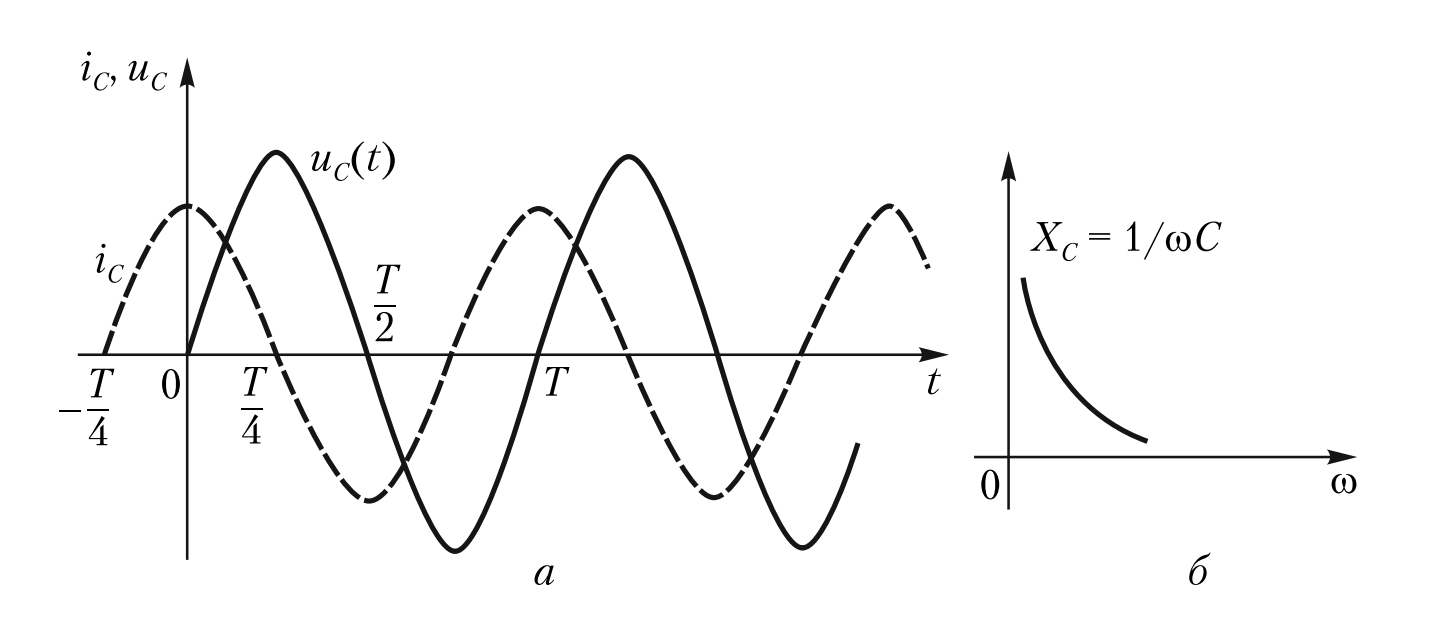
Рисунок 3. Синусоидальный режим в емкости:
а — временные диаграммы: напряжение \( u_C \) отстает от тока \( i_C \) на 90° (достигает максимума позже на четверть периода);
б — график частотной зависимости: емкостное сопротивление \( X_C = 1/(\omega C) \) гиперболически убывает с ростом частоты.

3.2. Емкостное сопротивление (Закон Ома для емкости)

Связь между амплитудными (а также действующими) значениями напряжения и тока описывается соотношением:

U_{mC} = \frac{I_m}{\omega C}

Это выражение структурно идентично закону Ома \( U = I \cdot R \). Роль сопротивления здесь играет величина \( X_C \), называемая реактивным емкостным сопротивлением:

X_C = \frac{1}{\omega C} = \frac{1}{2\pi f C}

Единица измерения \( X_C \) — Ом (\( \Omega \)).

3.3. Частотный анализ

Проанализируем зависимость \( X_C \) от частоты \( \omega \), показанную на Рисунке 3 (б):

При низких частотах (\( \omega \to 0 \)): \( X_C \to \infty \). Конденсатор представляет собой огромное сопротивление. Для постоянного тока (\( f=0 \)) это разрыв цепи.
При высоких частотах (\( \omega \to \infty \)): \( X_C \to 0 \). Конденсатор стремится стать перемычкой (коротким замыканием).

Именно это свойство используется в фильтрах: конденсаторы «не пускают» низкие частоты (блокировочные конденсаторы на входе усилителей) или же «закорачивают» высокочастотные помехи на землю (шунтирующие конденсаторы в цепях питания).

4. Реальная емкость: Схемы замещения и потери

До сих пор мы рассматривали идеальный элемент. Однако реальные физические компоненты (конденсаторы) не идеальны. Диэлектрик между обкладками обладает конечным сопротивлением, а выводы и обкладки обладают собственным омическим сопротивлением и индуктивностью.

Основной причиной потерь энергии в конденсаторе является несовершенство изоляции (токи утечки) и потери на переполяризацию диэлектрика.

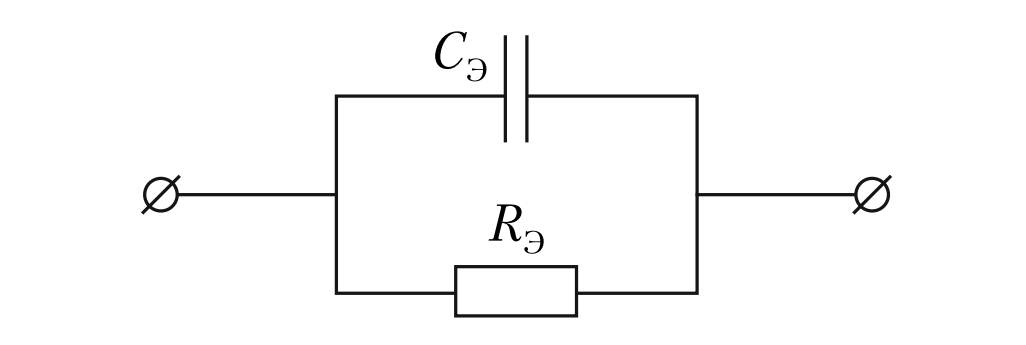
Рисунок 4. Простейшая параллельная схема замещения реального конденсатора. Она состоит из идеальной емкости \( C_Э \) и параллельно подключенного резистора \( R_Э \), моделирующего утечки.

На Рисунке 4 представлена параллельная схема замещения.

\( C_Э \) — основная емкость элемента.
\( R_Э \) — сопротивление утечки (очень большое для качественных конденсаторов, порядка мегаомов и выше).

Также существует последовательная схема замещения (ESR), которую чаще применяют для электролитических конденсаторов в импульсных источниках питания, но для общего анализа диэлектрических потерь параллельная схема весьма наглядна.

4.1. Добротность конденсатора

Качество конденсатора оценивается параметром, называемым добротностью (\( Q_C \)). Она показывает соотношение реактивной (запасаемой) мощности к активной (рассеиваемой).

В синусоидальном режиме для параллельной схемы замещения, представленной на рисунке, отношение проводимости емкостной ветви (\( \omega C_Э \)) к проводимости резистивной ветви (\( g_Э = 1/R_Э \)) определяет добротность:

Q_C = \frac{\text{Реактивная проводимость}}{\text{Активная проводимость}} = \frac{\omega C_Э}{1/R_Э} = \omega C_Э R_Э

Также часто используют обратную величину — тангенс угла диэлектрических потерь (\( \tan \delta \)):

\tan \delta = \frac{1}{Q_C}

Добротность реальных конденсаторов — величина безразмерная. У высококачественных керамических или пленочных конденсаторов на высоких частотах \( Q \) может достигать значений в несколько тысяч, что говорит об очень малых потерях энергии.

5. Практический пример: Расчет реактивного сопротивления и тока конденсатора

Необходимо определить, какой ток будет протекать через конденсатор в цепи переменного тока, и как частота сигнала влияет на это значение. Это классическая задача при проектировании фильтров и цепей питания.

Задача: Имеется неполярный пленочный конденсатор емкостью \( C = 2.2 \text{ мкФ} \) (микрофарада).
Необходимо рассчитать его реактивное сопротивление (\( X_C \)) и действующее значение тока (\( I \)) при подключении к источнику синусоидального напряжения \( U = 12 \text{ В} \) (RMS) для двух разных частот:

Случай А: Частота сети \( f_1 = 50 \text{ Гц} \) (низкая частота).
Случай Б: Частота аудиосигнала \( f_2 = 20 \text{ кГц} \) (высокая частота).

Решение задачи

Шаг 1. Перевод единиц измерения в систему СИ.

Емкость дана в микрофарадах. Для расчетов необходимо перевести её в Фарады:

C = 2.2 \text{ мкФ} = 2.2 \times 10^{-6} \text{ Ф} $$ $$ f_2 = 20 \text{ кГц} = 20 \times 10^3 \text{ Гц}

Шаг 2. Расчет для низкой частоты (\( f_1 = 50 \text{ Гц} \)).

Сначала найдем угловую частоту \( \omega \):

\omega_1 = 2\pi f_1 \approx 2 \cdot 3.14 \cdot 50 = 314 \text{ рад/с}

Теперь вычислим емкостное сопротивление \( X_{C1} \):

X_{C1} = \frac{1}{\omega_1 C} = \frac{1}{314 \cdot 2.2 \cdot 10^{-6}} \approx \frac{1}{0.0006908} \approx 1447 \text{ Ом} \approx 1.45 \text{ кОм}

По закону Ома для участка цепи находим ток:

I_1 = \frac{U}{X_{C1}} = \frac{12 \text{ В}}{1447 \text{ Ом}} \approx 0.0083 \text{ А} = 8.3 \text{ мА}

Шаг 3. Расчет для высокой частоты (\( f_2 = 20 \text{ кГц} \)).

Аналогично находим угловую частоту для 20 000 Гц:

\omega_2 = 2\pi f_2 \approx 6.28 \cdot 20000 = 125600 \text{ рад/с}

Вычисляем сопротивление \( X_{C2} \):

X_{C2} = \frac{1}{\omega_2 C} = \frac{1}{125600 \cdot 2.2 \cdot 10^{-6}} \approx \frac{1}{0.27632} \approx 3.6 \text{ Ом}

Находим ток:

I_2 = \frac{U}{X_{C2}} = \frac{12 \text{ В}}{3.6 \text{ Ом}} \approx 3.33 \text{ А}

Внимание! Обратите внимание на колоссальную разницу в токе. При одном и том же напряжении 12 Вольт, ток вырос с безопасных 8.3 мА до внушительных 3.33 А. Это наглядно демонстрирует, почему нельзя подключать обычные конденсаторы к высокочастотным мощным цепям без точного расчета — конденсатор может перегреться и взорваться, или сжечь источник сигнала, так как его сопротивление становится ничтожно малым (почти короткое замыкание).

Итоговое сравнение результатов

Параметр	Низкая частота (50 Гц)	Высокая частота (20 кГц)	Вывод
Сопротивление \( X_C \)	1447 Ом	3.6 Ом	Уменьшилось в 400 раз
Ток \( I \)	0.008 А (Малый)	3.33 А (Большой)	Вырос в 400 раз
Режим работы	Барьер (Сопротивление)	Почти проводник (Шунт)	Зависит от \( \omega \)

Данный расчет подтверждает теоретический тезис: проводимость емкости прямо пропорциональна частоте. Именно поэтому конденсаторы емкостью 2.2 мкФ могут использоваться как гасящее сопротивление в сетевых блоках питания (на 50 Гц), но будут мгновенно перегружать усилитель звуковой частоты, если их поставить параллельно выходу на 20 кГц.

6. Сравнительный анализ и применение

Сравним поведение конденсатора с другим реактивным элементом — индуктивностью, а также режимы его работы.

Таблица 1. Сравнение режимов работы емкости

Параметр / Режим	Постоянный ток (DC)	Переменный ток (AC)	Высокочастотный сигнал (HF)
Сопротивление (\( X_C \))	Бесконечность (\( \infty \))	\( 1 / (\omega C) \)	Стремится к нулю
Ток	0 (после заряда)	\( I = U / X_C \)	Максимальный
Роль в схеме	Разрыв цепи, накопитель заряда	Реактивное сопротивление, фазосдвигающий элемент	Шунт (короткое замыкание для ВЧ помех)

Таблица 2. Сравнительный анализ базовых пассивных элементов (R, L, C)

Свойства емкости в контексте других фундаментальных пассивных компонентов: резистора и индуктивности. В таблице ниже приведены ключевые характеристики, определяющие поведение этих элементов в цепях постоянного и переменного тока.

Характеристика	Резистор (R)	Индуктивность (L)	Конденсатор (C)
Основное физическое свойство	Диссипация: Безвозвратно преобразует электрическую энергию в тепловую (эффект Джоуля-Ленца). Ограничивает ток.	Инерция тока: Препятствует мгновенному изменению тока. Запасает энергию в магнитном поле.	Инерция напряжения: Препятствует мгновенному изменению напряжения. Запасает энергию в электрическом поле.
Дифференциальная связь \( u \) и \( i \)	\( u(t) = R \cdot i(t) \)	\( u(t) = L \frac{di(t)}{dt} \)	\( i(t) = C \frac{du(t)}{dt} \)
Сопротивление переменному току (Модуль)	\( R \) (не зависит от частоты)	\( X_L = \omega L \) (растет прямо пропорционально частоте)	\( X_C = \frac{1}{\omega C} \) (падает обратно пропорционально частоте)
Комплексное сопротивление (Импеданс)	\( Z_R = R \)	\( Z_L = j\omega L \)	\( Z_C = \frac{1}{j\omega C} = -j \frac{1}{\omega C} \)
Фазовый сдвиг (между u и i)	\( \varphi = 0^\circ \) (Ток и напряжение в фазе)	\( \varphi = +90^\circ \) (Напряжение опережает ток)	\( \varphi = -90^\circ \) (Ток опережает напряжение)
Поведение на постоянном токе (DC, \( \omega = 0 \))	Обычное сопротивление \( R \)	Короткое замыкание (проводник с \( R \approx 0 \))	Разрыв цепи (ток не течет)
Энергия	Рассеивается: \( P = I^2 R \)	Запасается в магнитном поле: \( W_L = \frac{L i^2}{2} \)	Запасается в электрическом поле: \( W_C = \frac{C u^2}{2} \)
Механическая аналогия	Трение (вязкость)	Масса (инерция)	Пружина (упругость)

7. Интересные факты о емкости и конденсаторах

Планета-конденсатор. Земной шар и ионосфера образуют гигантский сферический конденсатор. Обкладками служат проводящая поверхность Земли (отрицательный заряд) и ионосфера (положительный заряд), а диэлектриком — нижние слои атмосферы. Емкость этой системы составляет около 1 Фарада.
Тачскрины. Экраны современных смартфонов работают благодаря емкостной технологии. Стекло покрыто прозрачным проводящим слоем. Когда палец (который является проводником) касается экрана, он меняет локальную емкость в точке касания, что контроллер считывает как команду. Именно поэтому экраны не реагируют на обычные перчатки.
Смертельная «память». Высоковольтные конденсаторы (например, в микроволновых печах или старых ЭЛТ-мониторах) могут сохранять смертельный заряд в течение нескольких дней или даже месяцев после отключения прибора от сети. Это явление усугубляется эффектом диэлектрической абсорбции, когда заряд «впитывается» в диэлектрик и возвращается на обкладки после кратковременного замыкания.
Спасение жизней. В медицинских дефибрилляторах используется конденсатор большой емкости. Он накапливает энергию от батареи в течение нескольких секунд, чтобы затем мгновенно высвободить её мощным импульсом (около 3000 Вольт за несколько миллисекунд), способным перезапустить остановившееся сердце.
Суперконденсаторы (Ионисторы). Существуют устройства, занимающие промежуточное положение между аккумуляторами и обычными конденсаторами. Их емкость может достигать тысяч фарад. Они заряжаются за секунды и используются в электробусах для быстрой подзарядки на остановках, а также в системах рекуперации энергии торможения в Формуле-1 (KERS).
Микрофонный эффект. Некоторые керамические конденсаторы обладают пьезоэлектрическим эффектом: они могут механически вибрировать под воздействием переменного напряжения, издавая слышимый писк («поющие дроссели/конденсаторы» в видеокартах), и наоборот — преобразовывать внешние вибрации в электрический шум.
Лейденская банка. Первый в истории конденсатор, созданный в 1745 году, выглядел как стеклянная банка, оклеенная фольгой изнутри и снаружи. Чтобы получить емкость всего в 1 Фарад (стандарт для современного ионистора размером с монету), лейденскими банками пришлось бы заполнить площадь, превышающую территорию Москвы.

8. Часто задаваемые вопросы (FAQ)

1. Почему конденсаторы взрываются?

Чаще всего это происходит с электролитическими конденсаторами. Основные причины: превышение допустимого напряжения, переполюсовка (подключение плюса к минусу) или перегрев. Внутри электролита при этом закипает жидкость, давление газа растет, и корпус разрывается (обычно по специальным насечкам на крышке) с громким хлопком и выбросом «ватного» содержимого.

2. Можно ли заменить конденсатор на другой, с большим напряжением или емкостью?

Замена на конденсатор с большим рабочим напряжением всегда допустима и безопасна (если он влезает по габаритам). Замена на большую емкость допустима в цепях питания (фильтрах), но категорически запрещена во времязадающих цепях и колебательных контурах, так как это изменит частоту работы устройства.

3. Что такое ESR и почему оно важно?

ESR (Equivalent Series Resistance) — это эквивалентное последовательное сопротивление. У стареющих электролитических конденсаторов электролит высыхает, и ESR растет. Хотя емкость может оставаться в норме, высокое ESR приводит к тому, что конденсатор перестает сглаживать пульсации и начинает сильно греться. Это самая частая причина поломки импульсных блоков питания.

4. Почему конденсатор не пропускает постоянный ток?

Потому что его обкладки гальванически изолированы друг от друга слоем диэлектрика. Электроны не могут физически перепрыгнуть с одной пластины на другую. Ток в цепи течет только в моменты изменения напряжения (зарядка или разрядка), когда происходит перераспределение зарядов на пластинах. Как только емкость зарядится, движение зарядов прекращается.

5. В чем разница между керамическим и электролитическим конденсатором?

Керамические: имеют малую емкость, не имеют полярности, отлично работают на высоких частотах, долговечны.
Электролитические: имеют огромную емкость при малых размерах, имеют полярность (+/-), со временем высыхают и плохо работают на очень высоких частотах из-за внутренней индуктивности.

Заключение

Емкость является неотъемлемой частью современной электроники и электротехники. Процессы, протекающих в конденсаторе при постоянном и переменном токе — это основа для любого инженера. Мы выяснили, что конденсатор — это не просто разрыв цепи, а сложный частотно-зависимый элемент.

Умение рассчитывать реактивное сопротивление \( X_C \), понимать фазовый сдвиг (ток опережает напряжение) и учитывать паразитные параметры (утечку через \( R_Э \)) позволяет проектировать эффективные фильтры, источники питания, колебательные контуры и системы передачи данных. Правильный выбор типа конденсатора с учетом его добротности и частотных характеристик гарантирует надежность и долговечность разрабатываемых устройств.

Нормативная база

При проектировании электрических схем и чтении технической документации необходимо руководствоваться действующими государственными стандартами. Для Российской Федерации актуальны следующие документы:

ГОСТ 2.728-74 — «Единая система конструкторской документации. Обозначения условные графические в схемах. Резисторы, конденсаторы». (Описывает, как рисовать конденсаторы на схемах: обычные, электролитические, переменные).
ГОСТ 19880-74 — «Электротехника. Основные понятия. Термины и определения». (Определяет физические термины, такие как «емкость», «диэлектрик»).
ГОСТ Р МЭК 60384-1-2003 — «Конденсаторы постоянной емкости для электронной аппаратуры». (Общие технические условия, гармонизированные с международными стандартами IEC).

Список рекомендуемой литературы

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Издательство «Юрайт», 2024. — 701 с.
(Классический учебник, «библия» для инженеров-электриков, детально описывающая процессы в линейных и нелинейных цепях).
Демирчян К.С., Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники: в 3 т. — СПб.: Питер, 2021.
(Фундаментальный труд, глубоко раскрывающий физику электромагнитного поля и теории цепей).
Попов В.П. Основы теории цепей: Учебник для вузов. — М.: Издательство «Лань», 2020. — 576 с