Содержание страницы
- 1. Составление дифференциальных уравнений для однородной линии
- 2. Решение уравнений при установившемся синусоидальном процессе
- 3. Падающие и отраженные волны в линии
- 4. Линия без искажений (Условие Гевисайда)
- 5. Линия без потерь (Идеальная линия)
- Интересные факты по теме
- Часто задаваемые вопросы (FAQ)
- Заключение
Электрическими цепями с распределенными параметрами называются такие цепи, в которых физические свойства — сопротивление, индуктивность, емкость и проводимость — нельзя считать сосредоточенными в отдельных точках (как в случае с резисторами или конденсаторами). Вместо этого они равномерно или неравномерно «распределены» по всей длине проводников.
В таких цепях ток и напряжение являются функциями не только времени, но и пространственной координаты, то есть они непрерывно изменяются при переходе от одной точки (сечения) цепи к другой. Классическая теория цепей (законы Ома и Кирхгофа в их алгебраической форме) здесь неприменима; для анализа требуются дифференциальные уравнения в частных производных.
Краткая история: Теоретическая база для анализа таких цепей была заложена в 1880-х годах Оливером Хевисайдом. Он разработал так называемые «телеграфные уравнения», пытаясь решить проблему искажения и затухания сигнала в трансатлантических телеграфных кабелях. Его работа показала, что сигнал распространяется по кабелю в виде электромагнитной волны, и легла в основу современной теории линий передачи.
Термин «цепи с распределенными параметрами» (или более распространенный — «длинные линии») обычно связывают с мощными линиями электропередачи (ЛЭП), передающими энергию на большие расстояния, телефонными и телеграфными воздушными и кабельными линиями, рельсовыми цепями автоблокировки на железнодорожном транспорте, фидерами антенн в радиотехнике и другими подобными установками.
В то же время, устройства с распределенными параметрами встречаются и там, где «линий» в буквальном смысле этого слова, казалось бы, нет. Так, обычная индуктивная катушка при работе на повышенной частоте начинает проявлять свойства линии с распределенными параметрами. Действительно, между каждыми двумя соседними витками катушки есть межвитковая емкость. Кроме того, каждый виток обладает емкостью относительно корпуса прибора или «земли».
При частотах порядка сотен килогерц индуктивная катушка, если не принято специальных мер (например, секционирование или намотка типа «универсаль»), представляет собой типичную линию с распределенными параметрами. Если такая катушка намотана на стальной сердечник, который способен насыщаться, и частота тока достаточно велика, то все устройство в целом представляет собой сложную совокупность из электрической и магнитной нелинейных цепей с распределенными параметрами.
Сравнение моделей цепей
Для понимания контекста важно различать два подхода к моделированию электрических цепей.
| Характеристика | Цепи с сосредоточенными параметрами | Цепи с распределенными параметрами |
|---|---|---|
| Модель | Параметры R, L, C, G считаются сконцентрированными в дискретных элементах. | Параметры R, L, C, G равномерно распределены по всей длине линии. |
| Основное условие | Длина линии \(l\) значительно меньше длины волны \(\lambda\) (\(l \ll \lambda\)). | Длина линии \(l\) сопоставима или больше длины волны \(\lambda\) (\(l \ge \lambda/10\)). |
| Аналитический аппарат | Алгебраические уравнения (Закон Ома), обыкновенные дифференциальные уравнения (ОДУ). | Дифференциальные уравнения в частных производных (ДУЧП) — «телеграфные уравнения». |
| Ключевые явления | Переходные процессы, резонанс в контурах. | Распространение волн (падающие, отраженные), стоячие волны, волновое сопротивление. |
| Примеры | Низкочастотные схемы, блоки питания, RLC-фильтры на низких частотах. | Линии электропередачи (ЛЭП), коаксиальные кабели, волноводы, микрополосковые линии на платах. |
1. Составление дифференциальных уравнений для однородной линии
Рассмотрим однородную длинную линию (например, линию связи или электропередачи). У нее сопротивление, индуктивность, емкость и проводимость изоляции изменяются пропорционально ее длине. Для анализа разобьем всю линию на бесконечно малые элементарные участки длиной \(dx\). Координата \(x\) — это расстояние, отсчитываемое от начала линии.
Каждый такой участок \(dx\) (рис. 1) можно представить эквивалентной схемой, состоящей из четырех первичных параметров линии:
- \(R_0\) — продольное активное сопротивление единицы длины (Ом/км).
- \(L_0\) — индуктивность единицы длины (Гн/км).
- \(C_0\) — емкость единицы длины (Ф/км).
- \(G_0\) — поперечная проводимость утечки (изоляции) единицы длины (См/км).
Таким образом, на элементарной длине \(dx\) активное сопротивление будет равно \(R_0 dx\), индуктивность — \(L_0 dx\), проводимость утечки — \(G_0 dx\) и емкость — \(C_0 dx\). Отметим, что поперечная проводимость \(G_0\) не является обратной величиной по отношению к продольному сопротивлению \(R_0\).
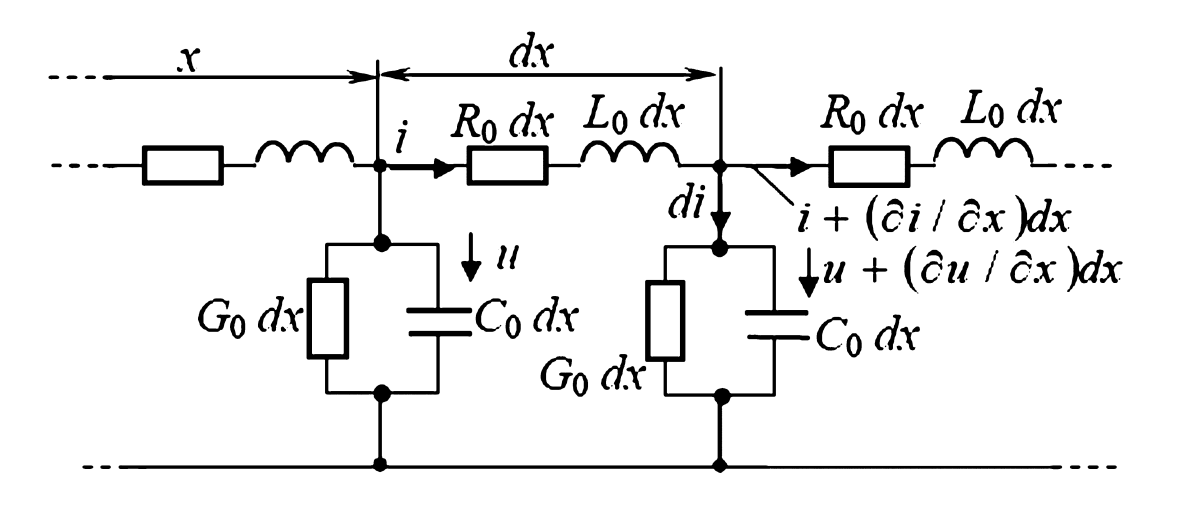
Обозначим ток в начале рассматриваемого участка линии (в сечении \(x\)) через \(i\), а напряжение между проводами линии в том же сечении — \(u\). И ток, и напряжение в общем случае являются функциями двух переменных: расстояния \(x\) и времени \(t\), т.е. \(i(x, t)\) и \(u(x, t)\). Поэтому в дальнейших уравнениях будут участвовать частные производные от \(u\) и \(i\) по времени \(t\) и расстоянию \(x\).
Если для некоторого момента времени \(t\) ток в начале участка (в сечении \(x\)) равен \(i\), то вследствие наличия утечки тока через поперечный элемент (проводимость \(G_0\) и емкость \(C_0\)) ток в конце участка (в сечении \(x+dx\)) для того же момента времени будет отличаться. Согласно разложению в ряд Тейлора, он будет равен \(i + \frac{\partial i}{\partial x} dx\). Здесь \(\frac{\partial i}{\partial x}\) — скорость изменения тока в направлении \(x\), которая, будучи умноженной на расстояние \(dx\), дает приращение тока на пути \(dx\). Аналогично, если напряжение в начале участка \(u\), то в конце участка для того же момента времени напряжение равно \(u + \frac{\partial u}{\partial x} dx\).
Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной \(dx\), обойдя его по часовой стрелке. Падение напряжения на продольных элементах \(R_0 dx\) и \(L_0 dx\) уравновешивается разностью напряжений между концом и началом участка:
$$ -u + (i R_0 dx) + (L_0 dx \frac{\partial i}{\partial t}) + (u + \frac{\partial u}{\partial x} dx) = 0 $$
После упрощения (члены \(u\) и \(-u\) взаимно уничтожаются) и деления всего уравнения на \(dx\), получим первое телеграфное уравнение:
$$ -\frac{\partial u}{\partial x} = L_0 \frac{\partial i}{\partial t} + R_0 i \quad (1) $$
Теперь применим первый закон Кирхгофа к узлу в сечении \(x\). Ток \(i\), входящий в узел, равен сумме тока, утекающего через поперечную ветвь (\(di\)), и тока, выходящего из узла в сечение \(x+dx\):
$$ i = di + (i + \frac{\partial i}{\partial x} dx) \quad (2) $$
Ток \(di\), в свою очередь, равен сумме токов, проходящих через проводимость \(G_0 dx\) и через емкость \(C_0 dx\). Напряжение на этих поперечных элементах можно принять равным \(u\), пренебрегая бесконечно малым падением напряжения \(\frac{\partial u}{\partial x} dx\) по сравнению с самим \(u\):
$$ di \approx (u) (G_0 dx) + (C_0 dx) \frac{\partial u}{\partial t} \quad (3) $$
Подставим (3) в (2), упростим (сократив \(i\)) и поделим полученное уравнение на \(dx\):
$$ 0 = (u G_0 + C_0 \frac{\partial u}{\partial t}) + \frac{\partial i}{\partial x} $$
Отсюда получаем второе телеграфное уравнение:
$$ -\frac{\partial i}{\partial x} = G_0 u + C_0 \frac{\partial u}{\partial t} \quad (4) $$
Уравнения (1) и (4) являются основными дифференциальными уравнениями для линии с распределенными параметрами. Это система линейных дифференциальных уравнений в частных производных.
2. Решение уравнений при установившемся синусоидальном процессе
На практике наиболее важен анализ линий в режиме установившегося синусоидального процесса. В этом случае мы можем перейти от функций времени \(i(x, t)\) и \(u(x, t)\) к их комплексным амплитудам (фазорам) \(\dot{I}(x)\) и \(\dot{U}(x)\), которые зависят только от координаты \(x\).
Для этого используем символический метод (метод комплексных амплитуд). Заменим мгновенные значения \(i\) и \(u\) на их комплексные представления \(\dot{I}(x) e^{j\omega t}\) и \(\dot{U}(x) e^{j\omega t}\). При этом операции дифференцирования по времени и пространству преобразуются:
- \(\frac{\partial i}{\partial t} \rightarrow j\omega \dot{I}(x)\)
- \(\frac{\partial u}{\partial t} \rightarrow j\omega \dot{U}(x)\)
- \(\frac{\partial i}{\partial x} \rightarrow \frac{d\dot{I}}{dx}\)
- \(\frac{\partial u}{\partial x} \rightarrow \frac{d\dot{U}}{dx}\)
Представление мгновенных значений в виде произведения двух множителей, из которых один является функцией только \(x\), а другой — функцией только \(t\), дает возможность перейти от уравнений в частных производных (1) и (4) к системе обыкновенных дифференциальных уравнений. Подставим эти выражения в (1) и (4) и сократим общий множитель \(e^{j\omega t}\). Получим:
$$ -\frac{d\dot{U}}{dx} = (R_0 + j\omega L_0) \dot{I} \quad (5) $$
$$ -\frac{d\dot{I}}{dx} = (G_0 + j\omega C_0) \dot{U} \quad (6) $$
Введем обозначения для комплексных погонных (на единицу длины) параметров линии:
$$ Z_0 = R_0 + j\omega L_0 \quad (7) $$
где \(Z_0\) — погонное комплексное сопротивление линии.
$$ Y_0 = G_0 + j\omega C_0 \quad (8) $$
где \(Y_0\) — погонная комплексная проводимость линии.
Тогда система (5) и (6) принимает вид:
$$ -\frac{d\dot{U}}{dx} = Z_0 \dot{I} \quad (5а) $$
$$ -\frac{d\dot{I}}{dx} = Y_0 \dot{U} \quad (6а) $$
Решим эту систему уравнений относительно \(\dot{U}\). С этой целью продифференцируем выражение (5а) по \(x\):
$$ -\frac{d^2\dot{U}}{dx^2} = Z_0 \frac{d\dot{I}}{dx} \quad (9) $$
В уравнение (9) вместо \(\frac{d\dot{I}}{dx}\) подставим правую часть уравнения (6а), т.е. \(-Y_0 \dot{U}\). Получим:
$$ -\frac{d^2\dot{U}}{dx^2} = Z_0 (-Y_0 \dot{U}) $$
$$ \frac{d^2\dot{U}}{dx^2} = Z_0 Y_0 \dot{U} \quad (10) $$
Уравнение (10) представляет собой линейное однородное дифференциальное уравнение второго порядка. Введем обозначение \(\gamma^2 = Z_0 Y_0\). Тогда уравнение (10) принимает канонический вид волнового уравнения:
$$ \frac{d^2\dot{U}}{dx^2} — \gamma^2 \dot{U} = 0 $$
Общее решение этого уравнения имеет вид:
$$ \dot{U}(x) = \dot{A}_1 e^{\gamma x} + \dot{A}_2 e^{-\gamma x} \quad (11) $$
Здесь \(\dot{A}_1\) и \(\dot{A}_2\) — комплексные числа, являющиеся постоянными интегрирования. Они определяются из граничных условий (например, через напряжение и ток в начале или в конце линии).
Коэффициент \(\gamma\) называется постоянной распространения (или коэффициентом распространения):
$$ \gamma = \sqrt{Z_0 Y_0} = \sqrt{(R_0 + j\omega L_0)(G_0 + j\omega C_0)} \quad (12) $$
\(\gamma\) — это комплексное число, поэтому его можно представить в алгебраической форме:
$$ \gamma = \alpha + j\beta \quad (13) $$
где \(\alpha\) — коэффициент затухания, характеризующий затухание (уменьшение амплитуды) волны на единицу длины линии (измеряется в Непер/км или дБ/км). \(\beta\) — коэффициент фазы (или волновое число), характеризующий изменение фазы волны на единицу длины линии (измеряется в рад/км).
Теперь определим ток \(\dot{I}(x)\) из уравнения (5а):
$$ \dot{I}(x) = -\frac{1}{Z_0} \frac{d\dot{U}}{dx} $$
Подставляем (11) и дифференцируем:
$$ \dot{I}(x) = -\frac{1}{Z_0} \frac{d}{dx} (\dot{A}_1 e^{\gamma x} + \dot{A}_2 e^{-\gamma x}) = -\frac{1}{Z_0} (\gamma \dot{A}_1 e^{\gamma x} — \gamma \dot{A}_2 e^{-\gamma x}) $$
$$ \dot{I}(x) = \frac{\gamma}{Z_0} (\dot{A}_2 e^{-\gamma x} — \dot{A}_1 e^{\gamma x}) $$
Величину \(\frac{Z_0}{\gamma} = \frac{Z_0}{\sqrt{Z_0 Y_0}} = \sqrt{\frac{Z_0}{Y_0}}\) обозначают \(Z_C\) и называют волновым сопротивлением (или характеристическим сопротивлением) линии:
$$ Z_C = \sqrt{\frac{Z_0}{Y_0}} = \sqrt{\frac{R_0 + j\omega L_0}{G_0 + j\omega C_0}} = z_C e^{j\phi_C} \quad (14) $$
где \(z_C\) — модуль, а \(\phi_C\) — аргумент волнового сопротивления \(Z_C\).
Поскольку \(\frac{\gamma}{Z_0} = \frac{1}{Z_C}\), выражение для тока принимает вид:
$$ \dot{I}(x) = \frac{1}{Z_C} (\dot{A}_2 e^{-\gamma x} — \dot{A}_1 e^{\gamma x}) \quad (15) $$
Уравнения (11) и (15) являются общими решениями для напряжения и тока в любой точке линии. Для удобства расчетов часто меняют начало отсчета, перенося его в конец линии. Обозначим расстояние от текущей точки на линии до конца линии через \(y\) и длину всей линии через \(l\):
$$ y = l — x \quad (16) $$
Пусть нам известны напряжение \(\dot{U}_2\) и ток \(\dot{I}_2\) в конце линии (т.е. при \(x=l\) или \(y=0\)). Подставим в формулы (11) и (15) \(x = l\). (Примечание: \(\dot{U}(x=l) = \dot{U}_2\), \(\dot{I}(x=l) = \dot{I}_2\)).
$$ \dot{U}_2 = \dot{A}_1 e^{\gamma l} + \dot{A}_2 e^{-\gamma l} $$
$$ \dot{I}_2 = \frac{1}{Z_C} (\dot{A}_2 e^{-\gamma l} — \dot{A}_1 e^{\gamma l}) $$
Решая эту систему относительно \(\dot{A}_1\) и \(\dot{A}_2\), находим постоянные интегрирования:
$$ \dot{A}_1 = \frac{1}{2} (\dot{U}_2 — \dot{I}_2 Z_C) e^{-\gamma l} \quad (17) $$
$$ \dot{A}_2 = \frac{1}{2} (\dot{U}_2 + \dot{I}_2 Z_C) e^{\gamma l} \quad (18) $$
Если подставить уравнения (17) и (18) в (11) и (15), заменить \(x = l — y\) и перейти к гиперболическим функциям (используя формулы Эйлера: \(\text{ch}(z) = \frac{e^z + e^{-z}}{2}\), \(\text{sh}(z) = \frac{e^z — e^{-z}}{2}\)), получим уравнения длинной линии в гиперболической форме:
$$ \dot{U}(y) = \dot{U}_2 \text{ch}(\gamma y) + \dot{I}_2 Z_C \text{sh}(\gamma y) \quad (19) $$
$$ \dot{I}(y) = \dot{U}_2 \frac{1}{Z_C} \text{sh}(\gamma y) + \dot{I}_2 \text{ch}(\gamma y) \quad (20) $$
Формулы (19) и (20) — это уравнения однородной линии в форме четырехполюсника. Они позволяют, зная напряжение \(\dot{U}_2\) и ток \(\dot{I}_2\) в конце линии (на нагрузке), определить комплексы напряжения и тока в любой точке, находящейся на расстоянии \(y\) от конца линии.
Определение \(Z_C\) и \(\gamma\) экспериментально:
Параметры \(Z_C\) и \(\gamma\) (вторичные параметры линии) можно определить, не зная первичных параметров, с помощью двух опытов: холостого хода (ХХ) и короткого замыкания (КЗ).
- Опыт холостого хода (\(I_2 = 0\)): Измеряем входное сопротивление \(Z_{XX}\) при разомкнутом конце линии.
Из (19) и (20) при \(y=l\) и \(\dot{I}_2 = 0\):
\(\dot{U}_1 = \dot{U}_2 \text{ch}(\gamma l)\)
\(\dot{I}_1 = \dot{U}_2 \frac{1}{Z_C} \text{sh}(\gamma l)\)
\(Z_{XX} = \frac{\dot{U}_1}{\dot{I}_1} = Z_C \frac{\text{ch}(\gamma l)}{\text{sh}(\gamma l)} = Z_C \coth(\gamma l)\) - Опыт короткого замыкания (\(U_2 = 0\)): Измеряем входное сопротивление \(Z_{КЗ}\) при замкнутом конце линии.
Из (19) и (20) при \(y=l\) и \(\dot{U}_2 = 0\):
\(\dot{U}_1 = \dot{I}_2 Z_C \text{sh}(\gamma l)\)
\(\dot{I}_1 = \dot{I}_2 \text{ch}(\gamma l)\)
\(Z_{КЗ} = \frac{\dot{U}_1}{\dot{I}_1} = Z_C \frac{\text{sh}(\gamma l)}{\text{ch}(\gamma l)} = Z_C \tanh(\gamma l)\)
Перемножив эти два сопротивления, найдем \(Z_C\):
\(Z_{XX} \cdot Z_{КЗ} = (Z_C \coth(\gamma l)) \cdot (Z_C \tanh(\gamma l)) = Z_C^2\)
\(Z_C = \sqrt{Z_{XX} \cdot Z_{КЗ}}\)
Разделив их, найдем \(\gamma\):
\(\frac{Z_{КЗ}}{Z_{XX}} = \frac{Z_C \tanh(\gamma l)}{Z_C \coth(\gamma l)} = \tanh^2(\gamma l)\)
\(\tanh(\gamma l) = \sqrt{\frac{Z_{КЗ}}{Z_{XX}}}\), откуда можно вычислить \(\gamma\).
3. Падающие и отраженные волны в линии
Вернемся к общему решению (11) и (15). Электромагнитный процесс в линии с распределенными параметрами определяется суммой двух процессов, представляющих собой падающие и отраженные волны.
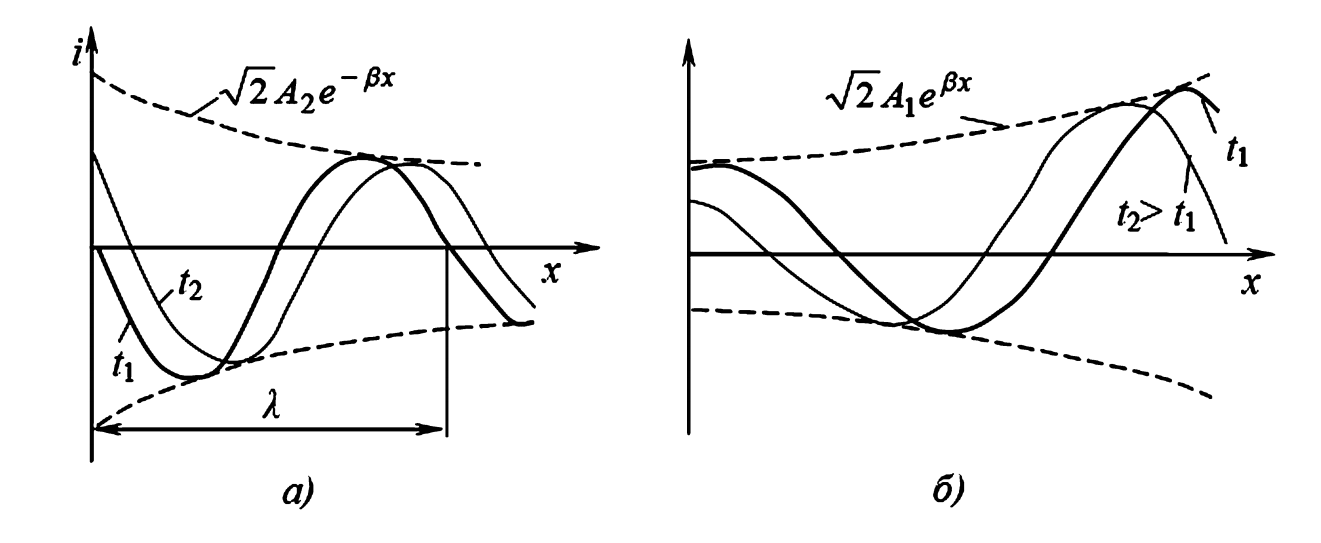
- Падающая (инцидентная) волна: Это процесс перемещения электромагнитной волны по направлению от источника энергии к приемнику (нагрузке), т. е. в направлении увеличения координаты \(x\). В наших уравнениях этому соответствует член \(\dot{A}_2 e^{-\gamma x}\). Множитель \(e^{-\gamma x} = e^{-\alpha x} \cdot e^{-j\beta x}\) показывает, что амплитуда волны (\(\dot{A}_2 e^{-\alpha x}\)) затухает по мере удаления от начала линии.
- Отраженная волна: Это процесс перемещения электромагнитной волны по направлению от приемника энергии (нагрузки) к источнику, т. е. в сторону уменьшения координаты \(x\). Этому соответствует член \(\dot{A}_1 e^{\gamma x}\). Множитель \(e^{\gamma x} = e^{\alpha x} \cdot e^{j\beta x}\) показывает, что эта волна затухает в своем направлении движения (к началу линии).
Таким образом, решение (11) для напряжения можно записать как сумму падающей и отраженной волн:
\( \dot{U}(x) = \dot{U}_{отр}(x) + \dot{U}_{пад}(x) = \dot{A}_1 e^{\gamma x} + \dot{A}_2 e^{-\gamma x} \)
Аналогично для тока из (15):
\( \dot{I}(x) = \dot{I}_{отр}(x) + \dot{I}_{пад}(x) = -\frac{\dot{A}_1}{Z_C} e^{\gamma x} + \frac{\dot{A}_2}{Z_C} e^{-\gamma x} \)
Обратите внимание, что для падающей волны \(\dot{U}_{пад} = Z_C \dot{I}_{пад}\), а для отраженной \(\dot{U}_{отр} = -Z_C \dot{I}_{отр}\). Волновое сопротивление \(Z_C\) связывает напряжение и ток в бегущей волне.
Коэффициент отражения
Отношение комплексной амплитуды отраженной волны к комплексной амплитуде падающей волны в конце линии (в точке \(x=l\)) называют коэффициентом отражения по напряжению \(\rho_U\).
$$ \rho_U = \frac{\dot{U}_{отр}(l)}{\dot{U}_{пад}(l)} = \frac{\dot{A}_1 e^{\gamma l}}{\dot{A}_2 e^{-\gamma l}} $$
Используя выражения для \(\dot{A}_1\) и \(\dot{A}_2\) (17) и (18), а также зная, что сопротивление нагрузки \(Z_Н = \dot{U}_2 / \dot{I}_2\), получаем:
$$ \rho_U = \frac{\frac{1}{2} (\dot{U}_2 — \dot{I}_2 Z_C) e^{-\gamma l} \cdot e^{\gamma l}}{\frac{1}{2} (\dot{U}_2 + \dot{I}_2 Z_C) e^{\gamma l} \cdot e^{-\gamma l}} = \frac{\dot{U}_2 — \dot{I}_2 Z_C}{\dot{U}_2 + \dot{I}_2 Z_C} = \frac{Z_Н — Z_C}{Z_Н + Z_C} \quad (21) $$
Аналогично, коэффициент отражения по току \(\rho_I\):
\( \rho_I = \frac{\dot{I}_{отр}(l)}{\dot{I}_{пад}(l)} = \frac{-\dot{A}_1 e^{\gamma l} / Z_C}{\dot{A}_2 e^{-\gamma l} / Z_C} = -\rho_U \)
Согласованная нагрузка
Линию с распределенными параметрами, как правило, используют в качестве промежуточного звена между источником энергии и нагрузкой. Из формулы (21) видно, что если сопротивление нагрузки \(Z_Н\) не равно волновому сопротивлению линии \(Z_C\), то \(\rho_U \neq 0\). В этом случае падающая волна, дойдя до конца линии, частично пройдет в нагрузку, а частично отразится от нее, порождая отраженную волну.
Если же выбрать нагрузку так, что \(Z_Н = Z_C\), то \(\rho_U = 0\). Такая нагрузка называется согласованной. При согласованной нагрузке отраженная волна отсутствует (\(\dot{A}_1 = 0\)), и вся энергия, приносимая падающей волной, полностью поглощается в нагрузке. Это режим бегущей волны, который является оптимальным для большинства линий связи и ВЧ-устройств.
4. Линия без искажений (Условие Гевисайда)
Линия без искажений — это такая линия, в которой электромагнитные волны всех частот распространяются с одинаковой фазовой скоростью и одинаково затухают. Это критически важно, например, для телефонии, где сложный сигнал (голос) состоит из множества гармоник. Если разные гармоники будут затухать по-разному или двигаться с разной скоростью, форма сигнала на выходе исказится, что приведет к искажению тембра голоса.
Линия будет неискажающей, если ее первичные параметры удовлетворяют особому соотношению, известному как условие Гевисайда:
$$ \frac{R_0}{L_0} = \frac{G_0}{C_0} = k $$
В этом случае волновое сопротивление (14) становится действительным числом, не зависящим от частоты:
\( Z_C = \sqrt{\frac{R_0 + j\omega L_0}{G_0 + j\omega C_0}} = \sqrt{\frac{k L_0 + j\omega L_0}{k C_0 + j\omega C_0}} = \sqrt{\frac{L_0(k + j\omega)}{C_0(k + j\omega)}} = \sqrt{\frac{L_0}{C_0}} \)
Постоянная распространения (12) также упрощается:
\( \gamma = \sqrt{(k L_0 + j\omega L_0)(k C_0 + j\omega C_0)} = \sqrt{L_0 C_0 (k + j\omega)^2} = (k + j\omega)\sqrt{L_0 C_0} \)
Сравнивая с \(\gamma = \alpha + j\beta\), получаем:
- Коэффициент затухания: \(\alpha = k \sqrt{L_0 C_0} = R_0 \sqrt{C_0/L_0}\) (не зависит от \(\omega\))
- Коэффициент фазы: \(\beta = \omega \sqrt{L_0 C_0}\) (линейно зависит от \(\omega\))
Фазовая скорость \(v_ф = \omega / \beta = 1 / \sqrt{L_0 C_0}\) также не зависит от частоты. Так как и \(\alpha\), и \(v_ф\) постоянны для всех частот, сигнал любой формы распространяется по такой линии без искажений, лишь затухая и задерживаясь по времени.
5. Линия без потерь (Идеальная линия)
На высоких и сверхвысоких частотах (ВЧ и СВЧ) часто выполняется условие \(R_0 \ll \omega L_0\) и \(G_0 \ll \omega C_0\). В этом случае активными потерями в линии можно пренебречь и рассматривать идеализированную линию без потерь (\(R_0 = 0\), \(G_0 = 0\)).
Для такой линии:
- \(Z_0 = j\omega L_0\)
- \(Y_0 = j\omega C_0\)
Тогда волновое сопротивление (14) становится чисто активным:
$$ Z_C = \sqrt{\frac{j\omega L_0}{j\omega C_0}} = \sqrt{\frac{L_0}{C_0}} \quad (22) $$
Постоянная распространения (12) становится чисто мнимой:
$$ \gamma = \sqrt{(j\omega L_0)(j\omega C_0)} = \sqrt{j^2 \omega^2 L_0 C_0} = j\omega \sqrt{L_0 C_0} $$
Отсюда \(\gamma = \alpha + j\beta\) дает:
- Коэффициент затухания: \(\alpha = 0\) (волна не затухает)
- Коэффициент фазы: \(\beta = \omega \sqrt{L_0 C_0}\)
Фазовая скорость \(v_ф = \omega / \beta = 1 / \sqrt{L_0 C_0}\). Линия без потерь автоматически является линией без искажений.
Уравнения линии без потерь
Для линии без потерь \(\gamma y = j\beta y\). Гиперболические функции от мнимого аргумента преобразуются в тригонометрические:
- \(\text{ch}(\gamma y) = \text{ch}(j\beta y) = \cos(\beta y)\)
- \(\text{sh}(\gamma y) = \text{sh}(j\beta y) = j \sin(\beta y)\)
Тогда уравнения (19) и (20) принимают вид:
$$ \dot{U}(y) = \dot{U}_2 \cos(\beta y) + j \dot{I}_2 Z_C \sin(\beta y) \quad (23) $$
$$ \dot{I}(y) = j \dot{U}_2 \frac{1}{Z_C} \sin(\beta y) + \dot{I}_2 \cos(\beta y) \quad (24) $$
Эти уравнения показывают, что в линии без потерь происходит периодическое изменение амплитуд напряжения и тока вдоль линии, но без потери энергии.
Режимы работы линии без потерь
1. Режим холостого хода (\(I_2 = 0\))
Входное сопротивление \(Z_{XX}(y)\) на расстоянии \(y\) от разомкнутого конца:
\( Z_{XX}(y) = \frac{\dot{U}(y)}{\dot{I}(y)} = \frac{\dot{U}_2 \cos(\beta y)}{j \dot{U}_2 (1/Z_C) \sin(\beta y)} = \frac{Z_C}{j} \cot(\beta y) \)
$$ Z_{XX}(y) = -j Z_C \cot(\beta y) \quad (25) $$
Входное сопротивление является чисто реактивным (емкостным или индуктивным) и зависит от длины линии \(y\). Например, при \(y = \lambda/4\) (\(\beta y = (2\pi/\lambda) \cdot (\lambda/4) = \pi/2\)), \(\cot(\pi/2) = 0\), и \(Z_{XX} = 0\). То есть, четвертьволновый отрезок линии, разомкнутый на конце, ведет себя как короткое замыкание (последовательный колебательный контур).
2. Режим короткого замыкания (\(U_2 = 0\))
Входное сопротивление \(Z_{КЗ}(y)\) на расстоянии \(y\) от замкнутого конца:
\( Z_{КЗ}(y) = \frac{\dot{U}(y)}{\dot{I}(y)} = \frac{j \dot{I}_2 Z_C \sin(\beta y)}{\dot{I}_2 \cos(\beta y)} \)
$$ Z_{КЗ}(y) = j Z_C \tan(\beta y) \quad (26) $$
При \(y = \lambda/4\) (\(\tan(\pi/2) \rightarrow \infty\)), \(Z_{КЗ} \rightarrow \infty\). Четвертьволновый отрезок, замкнутый на конце, ведет себя как разрыв цепи (параллельный колебательный контур). Это свойство широко используется в СВЧ-технике.
3. Режим стоячих волн
В линии без потерь при холостом ходе, коротком замыкании или чисто реактивной нагрузке \(\rho_U = 1\). Отраженная волна имеет ту же амплитуду, что и падающая. В результате их наложения образуется режим стоячих волн.
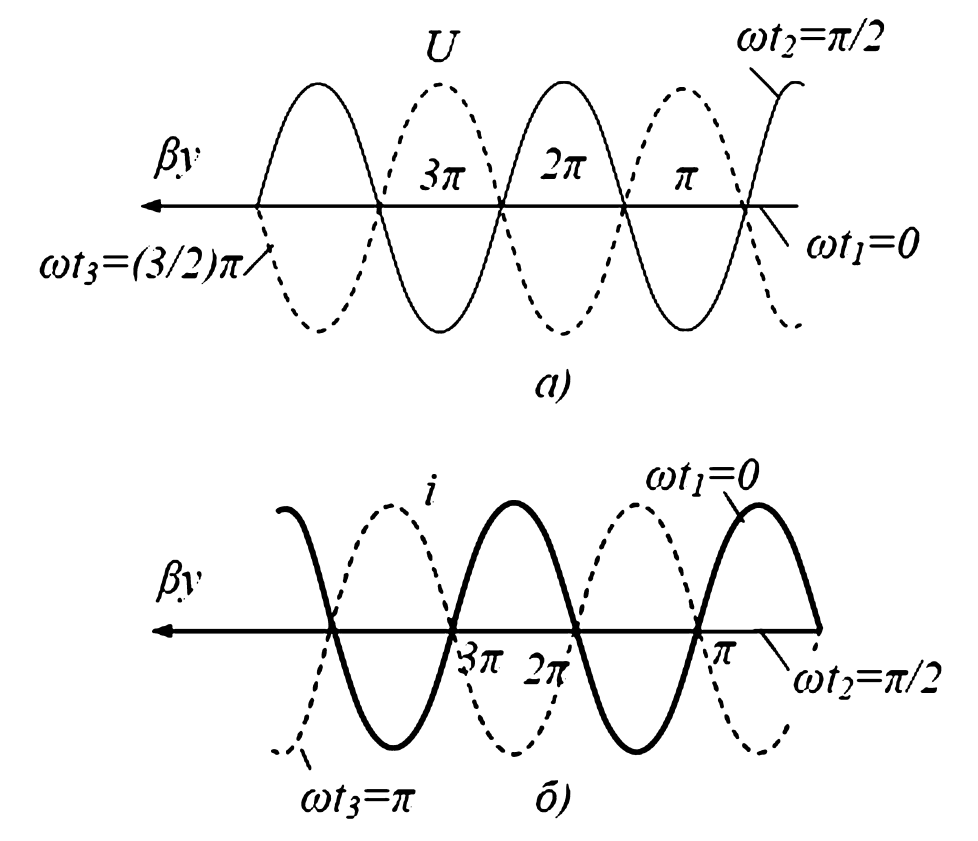
В режиме стоячей волны энергия от источника к нагрузке не передается. Энергия «заперта» в линии и периодически переходит из энергии электрического поля (в моменты максимума напряжения) в энергию магнитного поля (в моменты максимума тока).
Как видно из рис. 3, узлы тока совпадают с пучностями напряжения, и наоборот. В режиме КЗ картина будет обратной: в конце линии (y=0) будет узел напряжения и пучность тока.
4. Режим смешанных волн
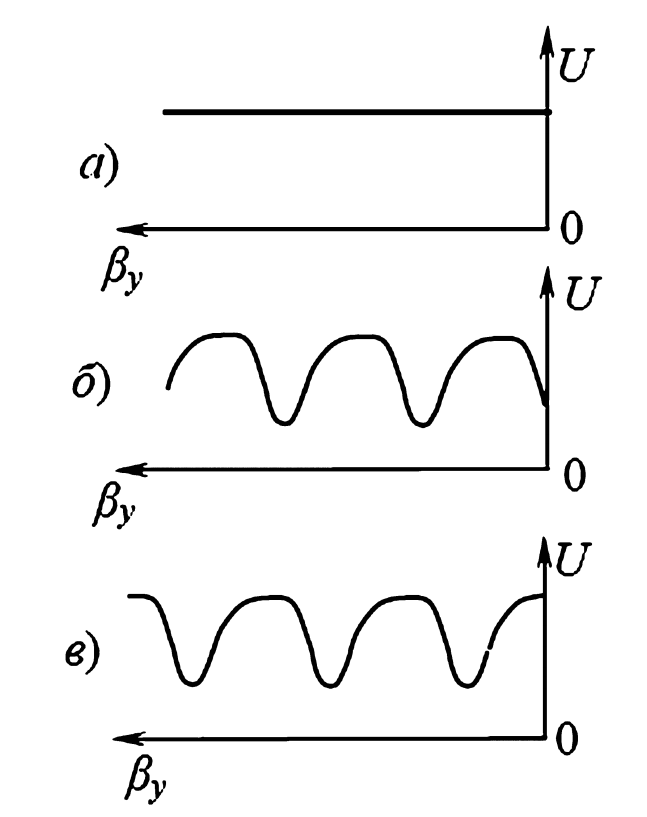
При несогласованной, но активной нагрузке (\(Z_Н \neq Z_C\) и \(\rho_U < 1\)), в линии возникает смешанная волна — комбинация бегущей волны (которая передает энергию в нагрузку) и стоячей волны (созданной отраженной частью).
Для оценки степени согласованности линии используют два коэффициента:
- Коэффициент стоячей волны (КСВ): \(K_{СВ} = \frac{U_{max}}{U_{min}} = \frac{1 + |\rho_U|}{1 — |\rho_U|}\).
В идеальном (согласованном) режиме \(\rho_U = 0\) и \(K_{СВ} = 1\). В режиме КЗ или ХХ \(\rho_U = 1\) и \(K_{СВ} \rightarrow \infty\). - Коэффициент бегущей волны (КБВ): \(K_{БВ} = \frac{U_{min}}{U_{max}} = \frac{1}{K_{СВ}}\).
Примеры расчетов
Пример 1
Задача: Для некоторой линии без потерь сопротивление нагрузки в 1.5 раза больше волнового (\(Z_Н = 1.5 Z_C\)). Определить коэффициент стоячей волны.
Решение:
1. Находим коэффициент отражения \(\rho_U\) (по модулю, т.к. нагрузки активные):
\( |\rho_U| = \left| \frac{Z_Н — Z_C}{Z_Н + Z_C} \right| = \left| \frac{1.5 Z_C — Z_C}{1.5 Z_C + Z_C} \right| = \frac{0.5 Z_C}{2.5 Z_C} = 0.2 \)
2. Находим коэффициент стоячей волны \(K_{СВ}\):
\( K_{СВ} = \frac{1 + |\rho_U|}{1 — |\rho_U|} = \frac{1 + 0.2}{1 — 0.2} = \frac{1.2}{0.8} = 1.5 \)
Ответ: \(K_{СВ} = 1.5\).
Пример 2
Задача: Для линии длиной \(l = 5\) км на частоте \(f = 1000\) Гц были проведены опыты ХХ и КЗ. Получены входные сопротивления: \(Z_{XX} = 535 e^{-j64^\circ}\) Ом и \(Z_{КЗ} = 467.5 e^{-j10^\circ}\) Ом. Требуется определить волновое сопротивление \(Z_C\) и коэффициент распространения \(\gamma\).
Решение:
1. Определяем волновое сопротивление \(Z_C\):
\( Z_C = \sqrt{Z_{XX} \cdot Z_{КЗ}} = \sqrt{(535 e^{-j64^\circ}) \cdot (467.5 e^{-j10^\circ})} \)
\( Z_C = \sqrt{535 \cdot 467.5} \cdot e^{j(-64^\circ — 10^\circ)/2} = \sqrt{249812.5} \cdot e^{-j74^\circ/2} \)
\( Z_C \approx 500 e^{-j37^\circ} \) Ом.
2. Определяем \(\tanh(\gamma l)\):
\( \tanh(\gamma l) = \sqrt{\frac{Z_{КЗ}}{Z_{XX}}} = \sqrt{\frac{467.5 e^{-j10^\circ}}{535 e^{-j64^\circ}}} = \sqrt{0.8738 e^{j(-10^\circ + 64^\circ)}} \)
\( \tanh(\gamma l) = \sqrt{0.8738} \cdot e^{j54^\circ/2} = 0.935 e^{j27^\circ} \)
3. Находим \(\gamma l\) из \(\tanh(\gamma l)\). Используем формулу \(e^{2z} = \frac{1 + \tanh(z)}{1 — \tanh(z)}\).
\( \tanh(\gamma l) = 0.935 (\cos 27^\circ + j \sin 27^\circ) = 0.935(0.891 + j0.454) \approx 0.833 + j0.424 \)
\( 1 + \tanh(\gamma l) = 1.833 + j0.424 = 1.88 e^{j13^\circ} \)
\( 1 — \tanh(\gamma l) = 0.167 — j0.424 = 0.455 e^{-j68.5^\circ} \)
\( e^{2\gamma l} = \frac{1.88 e^{j13^\circ}}{0.455 e^{-j68.5^\circ}} \approx 4.13 e^{j81.5^\circ} \)
4. Переходим к \(\gamma l\), взяв натуральный логарифм:
\( 2\gamma l = \ln(4.13 e^{j81.5^\circ}) = \ln(4.13) + j(81.5^\circ \cdot \frac{\pi}{180^\circ}) \approx 1.418 + j1.422 \)
\( \gamma l = 0.709 + j0.711 \)
5. Находим \(\gamma\), разделив на длину \(l = 5\) км:
\( \gamma = \frac{0.709 + j0.711}{5} = 0.1418 + j0.1422 \) 1/км.
В полярной форме \(\gamma \approx 0.2 e^{j45^\circ}\) 1/км. \(\alpha = 0.1418\) Нп/км, \(\beta = 0.1422\) рад/км.
Ответ: \(Z_C = 500 e^{-j37^\circ}\) Ом, \(\gamma = 0.1418 + j0.1422\) 1/км.
Пример 3
Задача: Определить первичные параметры \(R_0, L_0, G_0, C_0\) для линии из предыдущего примера, если \(f = 1000\) Гц, \(Z_C = 500 e^{-j37^\circ}\) Ом и \(\gamma = 0.2 e^{j45^\circ}\) 1/км.
Решение:
1. Находим погонное сопротивление \(Z_0 = R_0 + j\omega L_0\):
\( Z_0 = \gamma \cdot Z_C = (0.2 e^{j45^\circ}) \cdot (500 e^{-j37^\circ}) = 100 e^{j(45^\circ — 37^\circ)} = 100 e^{j8^\circ} \)
\( Z_0 = 100 (\cos 8^\circ + j \sin 8^\circ) = 100 (0.990 + j0.139) = 99 + j13.9 \)
Отсюда: \(R_0 = 99\) Ом/км.
\( \omega L_0 = 13.9 \Rightarrow L_0 = \frac{13.9}{2 \pi f} = \frac{13.9}{2 \pi \cdot 1000} \approx 0.00221 \) Гн/км (или 2.21 мГн/км).
\(L_0 = 2.21\) мГн/км.
2. Находим погонную проводимость \(Y_0 = G_0 + j\omega C_0\):
\( Y_0 = \frac{\gamma}{Z_C} = \frac{0.2 e^{j45^\circ}}{500 e^{-j37^\circ}} = 0.0004 e^{j(45^\circ + 37^\circ)} = 0.0004 e^{j82^\circ} \)
\( Y_0 = 0.0004 (\cos 82^\circ + j \sin 82^\circ) = 0.0004 (0.139 + j0.990) \)
\( Y_0 = (5.56 \cdot 10^{-5}) + j(3.96 \cdot 10^{-4}) \)
Отсюда: \(G_0 = 5.56 \cdot 10^{-5}\) См/км (или 55.6 мкСм/км).
\( \omega C_0 = 3.96 \cdot 10^{-4} \Rightarrow C_0 = \frac{3.96 \cdot 10^{-4}}{2 \pi \cdot 1000} \approx 6.3 \cdot 10^{-8} \) Ф/км.
\(C_0 = 0.063\) мкФ/км.
Ответ: \(R_0=99\) Ом/км, \(L_0=2.21\) мГн/км, \(G_0=55.6\) мкСм/км, \(C_0=0.063\) мкФ/км.
Интересные факты по теме
- Искусственная «пупинизация»: До открытия Оливером Хевисайдом условия неискажения (\(R_0/L_0 = G_0/C_0\)), сигналы в кабелях сильно искажались. Чтобы исправить это, американский инженер Михаил Пупин предложил искусственно увеличивать индуктивность \(L_0\) через равные промежутки, включая в линию специальные катушки («пупиновские катушки»). Это приближало линию к неискажающей и резко улучшало качество телефонной связи.
- Скорость света в кабеле: Фазовая скорость волны в линии без потерь \(v_ф = 1 / \sqrt{L_0 C_0}\). Для коаксиального кабеля с диэлектриком \(\varepsilon\) эта скорость равна \(v_ф = c / \sqrt{\varepsilon_r}\) , где \(c\) — скорость света в вакууме, а \(\varepsilon_r\) — относительная диэлектрическая проницаемость изолятора. В типичном кабеле \(\varepsilon_r \approx 2.25\), поэтому сигнал распространяется со скоростью \(\approx 0.67c\), то есть на 33% медленнее света.
- От кабеля до чипа: Теория длинных линий применяется не только к километровым ЛЭП. На современных компьютерных платах тактовые частоты достигают гигагерц. На таких частотах даже короткие дорожки (микрополосковые линии) длиной в несколько сантиметров становятся «длинными линиями» (\(l > \lambda/10\)), и их необходимо согласовывать, чтобы избежать отражений сигнала, вызывающих ошибки в данных.
- «Призраки» на ТВ: В эпоху аналогового телевидения плохое согласование антенного кабеля с телевизором (т.е. \(Z_Н \neq Z_C\)) приводило к отражению сигнала от входа телевизора обратно к антенне, где он отражался снова и шел в телевизор с задержкой. Это создавало на экране «призрачное», или двоение, изображение.
- Стоячие волны как на гитаре: Режим стоячей волны в линии без потерь физически аналогичен колебаниям струны гитары. Когда струну защипывают, в ней устанавливается стоячая волна с узлами на концах (у порожков). В линии КЗ или ХХ также возникают узлы и пучности, но для электромагнитной, а не механической волны.
Часто задаваемые вопросы (FAQ)
1. Почему цепи называются «с распределенными параметрами»?
Они так называются потому, что их фундаментальные электрические свойства (сопротивление R, индуктивность L, емкость C и проводимость G) не сосредоточены в отдельных компонентах, а «размазаны», или распределены, по всей длине проводников. Каждый миллиметр провода имеет свое малое сопротивление, свою малую индуктивность и свою малую емкость по отношению к другому проводу.
2. Когда нужно применять теорию длинных линий, а когда можно ее игнорировать?
Главный критерий — соотношение физической длины линии (\(l\)) и длины волны сигнала (\(\lambda\)). Практическое правило: если длина линии \(l\) составляет 10% или более от длины волны (\(l \ge \lambda/10\)), линию необходимо рассматривать как «длинную» (с распределенными параметрами). Если \(l \ll \lambda\), ее можно считать «короткой» и использовать теорию цепей с сосредоточенными параметрами (законы Ома/Кирхгофа), пренебрегая волновыми эффектами.
3. Что такое «первичные» и «вторичные» параметры линии?
Первичные параметры — это физические характеристики самой линии на единицу длины: \(R_0\) (Ом/км), \(L_0\) (Гн/км), \(C_0\) (Ф/км) и \(G_0\) (См/км). Они зависят от материала, геометрии проводов и изолятора.
Вторичные параметры — это расчетные характеристики, описывающие поведение волны в линии: \(Z_C\) (волновое сопротивление, Ом) и \(\gamma\) (постоянная распространения, 1/км). Они зависят от первичных параметров и частоты сигнала \(\omega\).
4. Что такое волновое сопротивление \(Z_C\) простыми словами?
Волновое сопротивление — это не обычное омическое сопротивление. Его нельзя измерить мультиметром. Это «кажущееся» сопротивление, которое «видит» электромагнитная волна, распространяясь по линии. Если бы линия была бесконечно длинной, ее входное сопротивление было бы равно \(Z_C\). В режиме бегущей волны (в согласованной линии) отношение напряжения к току \(\dot{U}/\dot{I}\) в любой точке равно \(Z_C\).
5. Почему так важно «согласование» нагрузки (\(Z_Н = Z_C\))?
Согласование критически важно для эффективной передачи энергии. Когда нагрузка согласована (\(Z_Н = Z_C\)), коэффициент отражения \(\rho_U = 0\). Это означает, что 100% энергии, приносимой падающей волной, поглощается нагрузкой. Если согласования нет (\(Z_Н \neq Z_C\)), часть энергии отражается обратно к источнику. Это снижает КПД, может повредить мощные передатчики и вызывает искажения сигнала (например, «призраки» на ТВ).
Заключение
Теория цепей с распределенными параметрами — фундаментальный раздел электротехники и радиотехники, описывающий процессы в линиях, длина которых сопоставима с длиной волны сигнала. В отличие от простых цепей, где ток одинаков во всех элементах, в «длинных линиях» ток и напряжение изменяются от точки к точке, подчиняясь волновым законам.
Ключевыми понятиями в этом анализе являются первичные параметры (\(R_0, L_0, C_0, G_0\)), определяющие физику линии, и вторичные параметры (\(Z_C\) и \(\gamma\)), описывающие распространение волны. Понимание явлений падающих и отраженных волн, волнового сопротивления и режима согласованной нагрузки является обязательным для проектирования эффективных систем передачи энергии и данных — от линий электропередачи до высокоскоростных цифровых устройств.
Нормативные документы
Анализ цепей с распределенными параметрами является теоретической базой, которая применяется при проектировании и испытаниях кабельной продукции. Первичные параметры (\(R_0, L_0, C_0, G_0\)) и вторичные (\(Z_C, \alpha\)) нормируются в стандартах на конкретные типы кабелей. Ключевые стандарты в этой области:
- ГОСТ 15845-2024 — Изделия кабельные. Термины и определения. (Устанавливает базовую терминологию).
- ГОСТ 22483-2012 (IEC 60228:2004) — Жилы токопроводящие для кабелей, проводов и шнуров. (Нормирует параметр \(R_0\)).
- ГОСТ Р 54429-2011 (IEC 61156-5:2009) — Кабели связи симметричные для цифровых систем передачи. (Нормирует волновое сопротивление, затухание и другие параметры для «витой пары»).
- ГОСТ 15125-92 — Кабели связи симметричные высокочастотные с кордельно-полистирольной изоляцией. (Устанавливает технические требования, включая волновое сопротивление и коэффициент затухания).
- ГОСТ 31996-2012 — Кабели силовые с пластмассовой изоляцией. (Регламентирует параметры, включая сопротивление и емкость, для силовых линий).
- ГОСТ 27893-2023 — Кабели связи. Методы испытаний. (Описывает методики измерения электрических параметров, включая \(Z_C\)).
Рекомендуемая литература
- Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Высшая школа, 2007.
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. — М.: Энергоатомиздат, 1989.
- Баскаков С.И. Радиотехнические цепи и сигналы. — М.: Высшая школа, 2005.
- Попов В.П. Основы теории цепей. — М.: Высшая школа, 2009.