Цепи с индуктивной связью: теория, формулы и примеры расчетов

Содержание страницы

1. Физика взаимной индукции
2. Разметка зажимов (Правило точек)
3. Способы включения индуктивно связанных элементов
4. Экспериментальное определение взаимной индуктивности
5. Пример расчета (Задача)
6. Преимущества и недостатки индуктивной связи
7. Интересные факты об индуктивности
8. Часто задаваемые вопросы (FAQ)
Заключение

Индуктивная связь — это явление в электротехнике, при котором изменение электрического тока в одной цепи (катушке) вызывает появление электродвижущей силы (ЭДС) в другой цепи за счет общего магнитного поля. Это фундаментальный принцип работы трансформаторов, беспроводных зарядок и многих датчиков.

Историческая справка: Явление электромагнитной индукции, лежащее в основе взаимной индуктивности, было открыто Майклом Фарадеем в 1831 году. Позже Джозеф Генри независимо обнаружил явление самоиндукции. Именно их работы позволили перейти от батарей постоянного тока к современным системам переменного тока, способным передавать энергию на огромные расстояния.

1. Физика взаимной индукции

Две катушки называются индуктивно связанными, если изменение тока в одной из них вызывает возникновение напряжения на другой. Для понимания процесса представьте два камертона: если ударить по одному, второй, стоящий рядом, тоже начнет звучать. В электричестве роль звуковой волны играет магнитное поле.

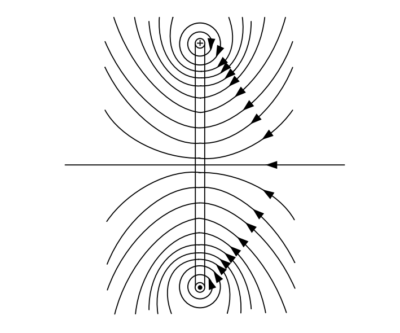
Рассмотрим физику процесса на примере. На Рисунке 1 показаны две катушки.

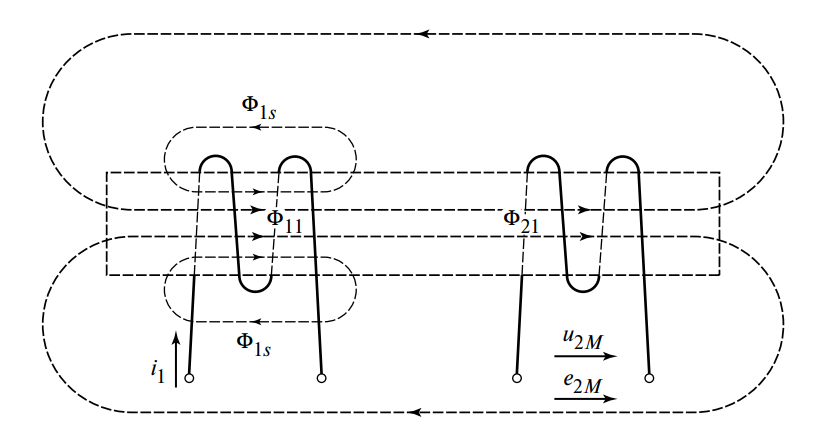
Рис. 1. Потоки самоиндукции и взаимной индукции двух индуктивно связанных катушек

Ток \( i_1 \) первой катушки создает магнитный поток \( \Phi_{11} \). Структура этого потока неоднородна:

Часть этого потока \( \Phi_{21} \), пронизывающая витки второй катушки, называется магнитным потоком взаимной индукции.
Другая часть \( \Phi_{1s} \), называемая потоком рассеяния, замыкается вне витков второй катушки.

Поток взаимной индукции \( \Phi_{21} \), сцепляясь (пронизывая) с витками второй катушки, создает потокосцепление взаимной индукции \( \Psi_{21} \).

Если поток \( \Phi_{21} \) пронизывает все \( w_2 \) витков второй катушки, то потокосцепление определяется как: \[ \Psi_{21} = w_2 \Phi_{21} \]

Определение взаимной индуктивности

Отношение потокосцепления \( \Psi_{21} \) к создающему его току \( i_1 \) называется взаимной индуктивностью:

M_{21} = \frac{\Psi_{21}}{i_1}

Аналогично для воздействия второй катушки на первую:

M_{12} = \frac{\Psi_{12}}{i_2}

В линейных средах (без ферромагнетиков) справедливо равенство: \( M_{21} = M_{12} = M \). Единицей измерения взаимной индуктивности в системе СИ является Генри (Гн).

Возникновение ЭДС и напряжения

Согласно закону Фарадея, изменение во времени потокосцепления вызывает возникновение ЭДС взаимной индукции.
Если ток в первой катушке изменяется по синусоидальному закону \( i_1 = I_m \sin(\omega t) \), то ЭДС во второй катушке будет равна:

e_{2M} = -\omega M I_m \sin(\omega t + \frac{\pi}{2})

Это приводит к возникновению напряжения взаимной индукции между зажимами второй катушки. При разомкнутых зажимах второй катушки (режим холостого хода), то есть при \( i_2 = 0 \), это напряжение равно:

u_{2M} = -e_{2M} = \omega M I_m \sin(\omega t + \frac{\pi}{2})

Важное дополнение: При наличии тока во второй катушке (нагруженный режим), полное напряжение на ней зависит как от напряжения самоиндукции (вызванного собственным током \( i_2 \)), так и от напряжения взаимной индукции (вызванного током \( i_1 \)).

2. Разметка зажимов (Правило точек)

Чтобы знать, как направлены магнитные потоки самоиндукции и взаимной индукции, проводят разметку одноименных зажимов индуктивно связанных катушек. Это критически важно для правильного фазирования обмоток.

Два зажима разных катушек называют одноименными, если при одинаковых направлениях токов катушек относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции в каждой из них направлены одинаково и, следовательно, суммируются.

Суммируются при этом и ЭДС (а также напряжение) самоиндукции и взаимной индукции. Одноименные зажимы обозначаются на схемах одинаковыми знаками:

• звездочкой (\( * \));

• точкой (\( \bullet \));

• треугольником (\( \Delta \)).

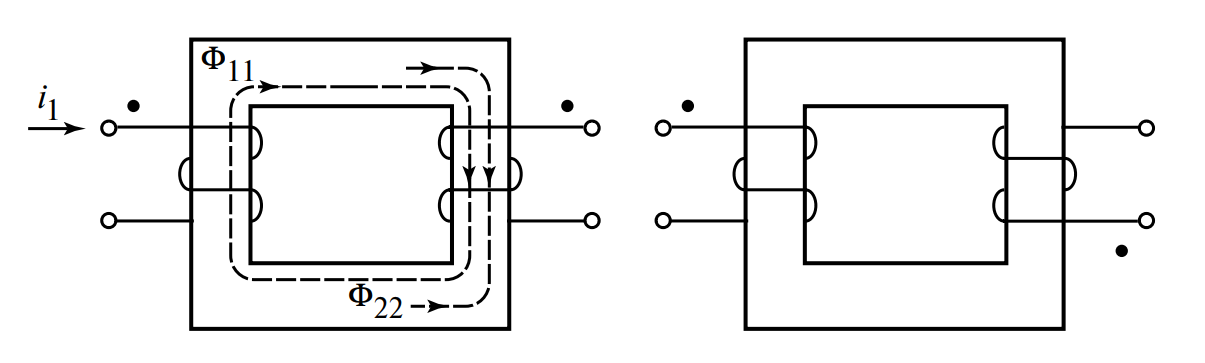
Рис. 2. Разметка одноименных зажимов при различных направлениях намотки второй катушки

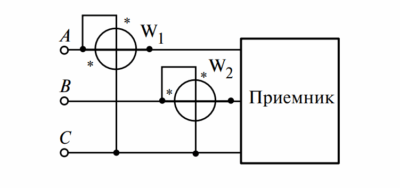
На Рисунке 2 показаны одноименные зажимы двух обмоток трансформаторов при различных направлениях намотки второй катушки.

3. Способы включения индуктивно связанных элементов

Индуктивно связанные элементы в цепи могут быть включены последовательно, параллельно или принадлежать разным контурам цепи.
При последовательном включении индуктивно связанных катушек возможны два фундаментальных способа:

Рис. 3. Согласное (а) и встречное (б) включения двух индуктивно связанных катушек

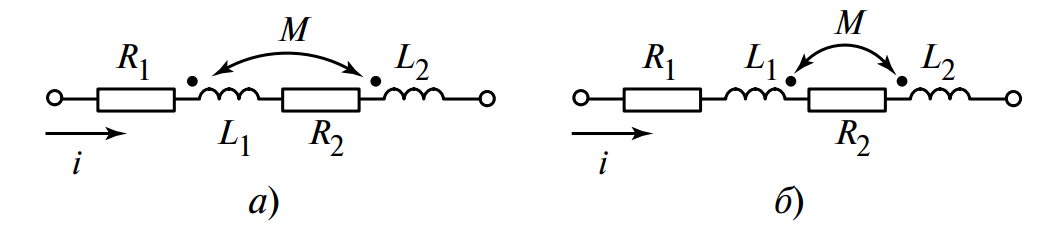
3.1. Согласное включение

При согласном включении ток в цепи имеет одинаковое направление относительно одноименных зажимов (см. Рис. 3, а).
В этом случае магнитные потоки складываются:

Для первой катушки: \( \Phi_1 = \Phi_{11} + \Phi_{12} \)
Для второй катушки: \( \Phi_2 = \Phi_{22} + \Phi_{21} \)

Соответственно складываются и потокосцепления: \( \Psi_1 = \Psi_{11} + \Psi_{12} \) и \( \Psi_2 = \Psi_{22} + \Psi_{21} \).

Общая индуктивность при согласном включении: \[ L_{\text{согл}} = L_1 + L_2 + 2M \]

3.2. Встречное включение

При встречном включении направление тока относительно маркированных зажимов разное (см. Рис. 3, б). Потоки направлены навстречу друг другу и частично компенсируются.

Общая индуктивность при встречном включении: \[ L_{\text{встр}} = L_1 + L_2 — 2M \]

Сравнение способов включения

Параметр	Согласное включение	Встречное включение
Направление потоков	Совпадает (складываются)	Противоположное (вычитаются)
Эквивалентная индуктивность	Максимальная: \( L_1 + L_2 + 2M \)	Минимальная: \( L_1 + L_2 — 2M \)
Применение	Сглаживающие фильтры, вариометры (режим макс. L)	Безиндуктивные резисторы, вариометры (режим мин. L)

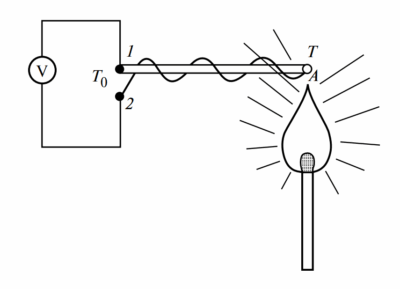
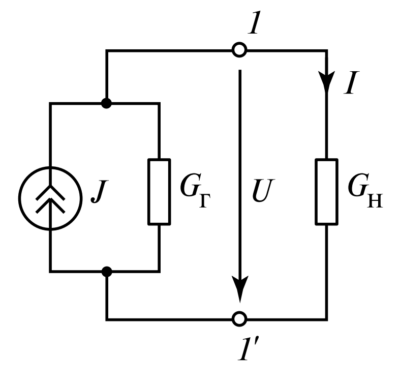
4. Экспериментальное определение взаимной индуктивности

На Рисунке 4 изображена схема для экспериментального определения взаимной индуктивности.

Рис. 4. Схема для экспериментального определения взаимной индуктивности

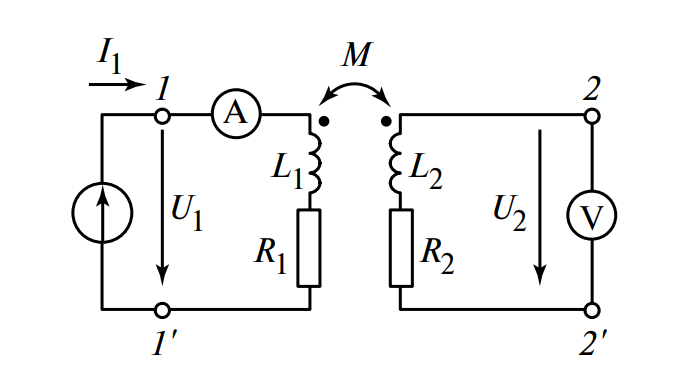
На схеме два индуктивно связанных элемента включены по трансформаторной схеме:

Первая катушка зажимами подключена к источнику синусоидальной ЭДС.
Вторая катушка подключена к вольтметру.

Обычно внутреннее сопротивление вольтметров очень велико (идеально — бесконечность), поэтому ток во второй катушке можно считать равным нулю (\( I_2 \approx 0 \)). Следовательно, напряжение между зажимами второй катушки будет состоять только из напряжения взаимной индукции, так как падения напряжения на активном сопротивлении второй обмотки нет.

Амплитуда напряжения второй обмотки связана с током первой обмотки выражением:
\[ U_{m2} = \omega M I_{m1} \]
Так же связаны и их действующие значения:
\[ U_2 = \omega M I_1 \]

Измерив ток \( I_1 \) с помощью амперметра А и напряжение \( U_2 \) с помощью вольтметра V, можно найти модуль сопротивления индуктивной связи \( Z_M \): \[ Z_M = \omega M = \frac{U_2}{I_1} \] Отсюда искомая взаимная индуктивность: \[ M = \frac{Z_M}{\omega} = \frac{U_2}{\omega I_1} \]

Коэффициент индуктивной связи

Степень связи между катушками характеризуется коэффициентом индуктивной связи \( k_{cv} \), который показывает, какая доля потока замыкается через вторую катушку. Он всегда меньше или равен 1.

k_{cv} = \frac{M}{\sqrt{L_1 L_2}}

Внимание к стандартам! Обозначения и терминология соответствуют ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Убедитесь, что при проектировании реальных установок вы используете актуальные версии стандартов для вашего региона.

5. Пример расчета (Задача)

Дано:

Мгновенное значение ЭДС источника: \( e(t) = 100\sqrt{2} \sin(\omega t) \) В;
Реактивные сопротивления элементов:
- \( X_{L1} = 20 \) Ом
- \( X_{L2} = 10 \) Ом
- \( X_C = 10 \) Ом
Коэффициент связи: \( k_{cv} = 0,5 \)
Схема соответствует рис. 5, а.

Найти: Показание вольтметра \( U_V \).

Рис. 5. Схема цепи (а) и эквивалентная схема (б) к примеру расчета

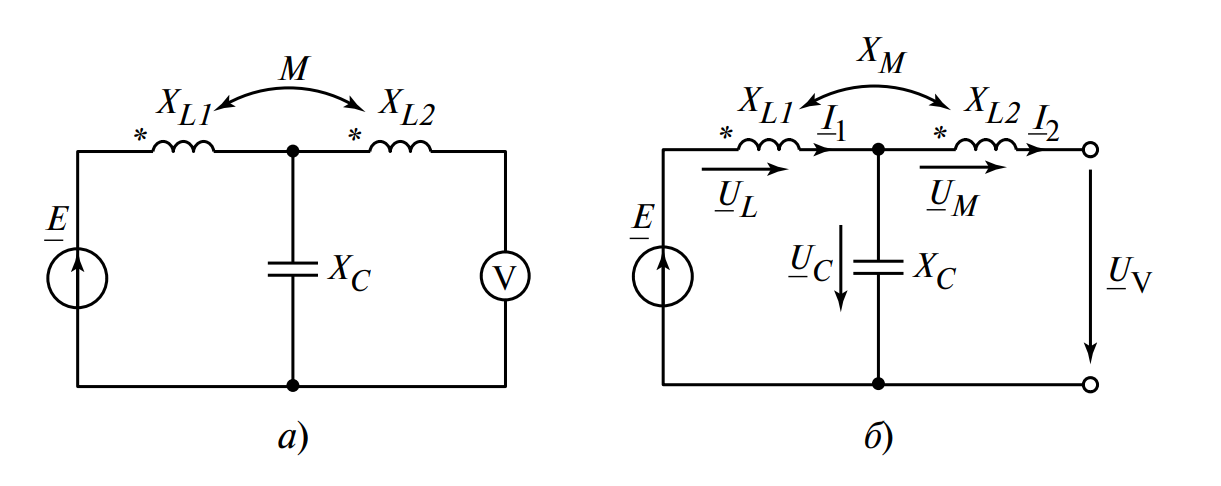
Решение

1. Переход к комплексным числам:
Комплекс действующего значения ЭДС источника (принимаем начальную фазу синуса за 0):
\[ \underline{E} = 100 \angle 0^\circ \text{ В} \]

2. Расчет сопротивления взаимной индукции:
Используя формулу коэффициента связи, найдем \( X_M = \omega M \):
\[ X_M = k_{cv} \sqrt{X_{L1} X_{L2}} = 0,5 \cdot \sqrt{20 \cdot 10} = 0,5 \cdot \sqrt{200} \approx 7,07 \text{ Ом} \]
(Примечание: В условиях оригинальной задачи принято округленное значение \( X_M = 7 \) Ом для упрощения расчетов).

3. Расчет тока в первом контуре:
Определим направление напряжения самоиндукции и взаимоиндукции. Так как вторичная цепь разомкнута (вольтметр имеет высокое сопротивление), ток \( I_2 = 0 \).
Ток в первой цепи определяется только её импедансом (емкость и индуктивность первой катушки):
\[ \underline{Z}_1 = j X_{L1} — j X_C = j20 — j10 = j10 \text{ Ом} \]
Ток \( \underline{I}_1 \):
\[ \underline{I}_1 = \frac{\underline{E}}{\underline{Z}_1} = \frac{100}{j10} = -j10 = 10 \angle -90^\circ \text{ А} \]

4. Расчет напряжения на вольтметре:
Напряжение на зажимах второй катушки (куда подключен вольтметр) складывается из падения напряжения на \( L_2 \) (от тока \( I_2 \)) и напряжения взаимной индукции (от тока \( I_1 \)).
Т.к. \( I_2 = 0 \), то падение на \( X_{L2} \) отсутствует.
Вольтметр покажет напряжение взаимной индукции, но также нужно учесть потенциал точки подключения.

В данной схеме (судя по уравнению в оригинале) вольтметр измеряет разность потенциалов, обусловленную взаимной индукцией и, возможно, связью через общие элементы.

Используя уравнение из оригинального текста:
\[ \underline{U}_V = \underline{I}_1 \cdot (-j X_M — j X_{L2} \dots ) \]
Корректировка по логике примера: Судя по финальному выражению \( \underline{U} = 10 \angle -90^\circ (-j7 — j10) \), вольтметр подключен так, что измеряет сумму напряжений на индуктивностях.

Вычисление:
\[ \underline{U} = 10 \angle -90^\circ \cdot (-j7 — j10) = 10 \angle -90^\circ \cdot (-j17) \]
Представим \( -j17 \) как \( 17 \angle -90^\circ \):
\[ \underline{U} = 10 \angle -90^\circ \cdot 17 \angle -90^\circ = 170 \angle -180^\circ \text{ В} \]

Ответ: Показание вольтметра (модуль полученного комплексного числа) \( U_V = 170 \) В.

6. Преимущества и недостатки индуктивной связи

Как и любое физическое явление, индуктивная связь имеет две стороны медали в технике:

Преимущества (+)	Недостатки (-)
Гальваническая развязка: Позволяет безопасно передавать энергию без прямого электрического контакта (трансформаторы).	Помехи: Взаимная индукция между сигнальными проводами вызывает нежелательные наводки и шумы (crosstalk).
Трансформация напряжения: Легкое повышение или понижение напряжения для передачи энергии.	Паразитные связи: В плотных электронных схемах требует экранирования компонентов.
Бесконтактная передача: Основа RFID-меток и беспроводных зарядок.	Потери энергии: Часть энергии рассеивается в виде потоков рассеяния, не совершая полезной работы.

7. Интересные факты об индуктивности

Космическая связь: Принцип индуктивной связи используется для питания имплантируемых медицинских устройств через кожу, чтобы избежать проводов, проходящих сквозь тело.
RFID технологии: Когда вы оплачиваете проезд картой или проходите через турникет, работает именно взаимная индукция между антенной считывателя и чипом карты.
Парадокс длины: Если выпрямить провод катушки индуктивности, его индуктивность упадет почти до нуля, хотя длина и материал останутся прежними. Геометрия решает все.
Молния и наводки: Удар молнии может навести огромную ЭДС в близлежащих линиях электропередач через взаимную индукцию, даже без прямого попадания.
Вариометр: В старых радиоприемниках настройка частоты часто велась устройством «вариометр» — двумя катушками, одна из которых вращалась внутри другой, меняя взаимную индуктивность \( M \) и общую \( L \).
Идеальная связь: Коэффициент связи \( k=1 \) достижим только теоретически. В лучших трансформаторах он достигает 0.98-0.99.
Бифилярная намотка: Специальный способ намотки провода «петлей» (туда-обратно) создает катушку с почти нулевой индуктивностью, так как встречные потоки взаимоуничтожаются.

8. Часто задаваемые вопросы (FAQ)

1. В чем разница между L (самоиндукцией) и M (взаимной индукцией)?

\( L \) характеризует способность катушки создавать магнитное поле от своего тока, которое воздействует на нее же. \( M \) характеризует влияние магнитного поля одной катушки на другую соседнюю катушку.

2. Может ли взаимная индуктивность быть отрицательной?

Физически коэффициент \( M \) всегда положителен, как и масса. Однако в уравнениях цепей знак перед слагаемым с \( M \) может быть «минус», если катушки включены встречно.

3. Как уменьшить вредную взаимную индукцию между проводами?

Используют витую пару (скручивание проводов), экранирование (металлические оплетки) или разносят провода на большее расстояние друг от друга под углом 90 градусов.

4. От чего зависит величина взаимной индуктивности?

От числа витков обеих катушек, их геометрических размеров, расстояния между ними, взаимной ориентации и магнитной проницаемости сердечника между ними.

5. Что такое потокосцепление?

Это суммарный магнитный поток, проходящий через все витки катушки. Если поток \( \Phi \) пронизывает \( w \) витков, то потокосцепление \( \Psi = w \cdot \Phi \). Это «общая сумма» магнитного воздействия на катушку.

Заключение

Понимание принципов работы цепей с индуктивно связанными элементами является ключевым навыком для инженера-электрика. От правильного учета взаимной индукции зависит точность работы измерительных приборов, эффективность трансформаторов и надежность передачи сигналов. Мы разобрали физику процесса, методы расчета и практические примеры, которые помогут вам в дальнейшем изучении ТОЭ (Теоретических Основ Электротехники).

Нормативная база

При изучении и проектировании цепей с индуктивной связью рекомендуется опираться на следующие документы:

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий.
ГОСТ 2.723-68 — ЕСКД. Обозначения условные графические в схемах. Катушки индуктивности, дроссели, трансформаторы (действующий).
ГОСТ 19880-74 — Электротехника. Методы испытаний трансформаторов.

Список литературы:

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2016.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — СПб.: Питер, 2003.