Анализ цепей при непериодических (импульсных) воздействиях

Содержание страницы

Математический аппарат спектрального метода
Сравнение спектрального и операторного методов
Преимущества и недостатки спектрального метода
Частотные спектры типовых одиночных сигналов
Теорема Рейли
Применение спектрального метода
Интересные факты по теме
Часто задаваемые вопросы (FAQ)
Заключение

Спектральный (частотный) метод — это фундаментальный подход в теории электрических цепей, предназначенный для анализа их реакции на непериодические, в том числе импульсные, сигналы. Этот метод также применяется для расчета переходных процессов, выступая альтернативой операторному методу.

Суть метода заключается в преобразовании функций времени \((f(t))\), описывающих сигналы (напряжения, токи), в функции частоты \((S(j\omega))\), которые называются спектрами или спектральными плотностями. Исторически этот метод вырос из работ французского математика Жана-Батиста Жозефа Фурье, который в начале XIX века, изучая процессы теплопроводности, предположил, что любую функцию можно представить в виде суммы (или интеграла) синусоидальных колебаний. Это привело к созданию рядов Фурье (для периодических сигналов) и интеграла Фурье (для непериодических), который является математической основой спектрального метода.

Математический аппарат спектрального метода

Переход от временной области к частотной осуществляется с помощью прямого преобразования Фурье, которое представляет собой интеграл Фурье:

\[ S(j\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt \]

Это выражение получают из формулы для ряда Фурье путем предельного перехода, при котором период функции \((T)\) устремляется к бесконечности.

Важное ограничение: Для существования преобразования Фурье функция \((f(t))\) должна быть абсолютно интегрируемой, то есть интеграл от ее модуля должен быть конечным:

\[ \int_{-\infty}^{\infty} |f(t)| dt < \infty \]

Ряд функций, например, функция единичного скачка или постоянное напряжение, этому условию не удовлетворяет, что ограничивает применимость метода в сравнении с преобразованием Лапласа.

Для обратного перехода, то есть для нахождения исходной функции времени \((f(t))\) по известному спектру \((S(j\omega))\), используется обратное преобразование Фурье:

\[ f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} S(j\omega) e^{j\omega t} d\omega \]

Связь с преобразованием Лапласа

Сравнивая формулы преобразований Лапласа \((F(p))\) и Фурье \((S(j\omega))\), можно сделать важный вывод: преобразование Фурье является частным случаем преобразования Лапласа при замене комплексной переменной \((p)\) на \((j\omega)\).

\[ S(j\omega) = F(p) \Big|_{p=j\omega} \]

Это означает, что все ранее рассмотренные формулы соответствия и свойства преобразования Лапласа (теоремы о дифференцировании, интегрировании, смещении и т.д.) справедливы и для преобразования Фурье. Например, закон Ома для участка цепи RLC, записанный в операторной форме, в спектральной форме будет иметь вид:

\[ I(j\omega) = \frac{E(j\omega) + Li(0) — \frac{U_C(0)}{j\omega}}{R + j\omega L + \frac{1}{j\omega C}} \]

Знаменатель этого выражения:

\[ Z(j\omega) = R + j\omega L + \frac{1}{j\omega C} \]

представляет собой не что иное, как комплексное сопротивление (импеданс) цепи, которое широко применяется для расчета цепей синусоидального тока в установившемся режиме. Таким образом, спектральный метод напрямую связывает анализ переходных процессов с хорошо изученными частотными характеристиками цепи.

Алгоритм расчета

Если входной сигнал имеет вид некоторого импульса \((u_1(t))\), то, определив его спектр \((S(j\omega) = U_1(j\omega))\) и зная частотную характеристику (импеданс \((Z(j\omega))\) или передаточную функцию \((H(j\omega))\) цепи), можно определить спектр искомой величины (например, тока \((I(j\omega))\) или выходного напряжения \((U_2(j\omega))\)).

Для четырехполюсника, зная его передаточную функцию \((H(j\omega))\), спектр выходного сигнала определяется как произведение:

\[ U_2(j\omega) = H(j\omega) S(j\omega) \]

Затем, применив к \((U_2(j\omega))\) обратное преобразование Фурье, можно определить зависимость выходного сигнала от времени \((u_2(t))\).

АЧХ и ФЧХ: Спектр функции \((S(j\omega))\), передаточная функция \((H(j\omega))\) и любая другая частотная характеристика являются комплексными величинами. Их можно представить в нескольких видах, например, в алгебраической \((B(\omega) + jM(\omega))\) или показательной форме:

\[ H(j\omega) = H(\omega) e^{j\theta(\omega)} \]

Здесь:

\(\mathbf{H(\omega)}\) — амплитудно-частотная характеристика (АЧХ), или модуль комплексной функции. Она показывает, как цепь усиливает или ослабляет различные частотные составляющие сигнала.
\(\mathbf{\theta(\omega)}\) — фазочастотная характеристика (ФЧХ), или аргумент комплексной функции. Она показывает, какой фазовый сдвиг вносит цепь для каждой частотной составляющей.

Сравнение спектрального и операторного методов

Хотя оба метода служат для анализа переходных процессов, они имеют ключевые различия, делающие их более или менее предпочтительными в разных ситуациях.

Параметр	Спектральный метод (Фурье)	Операторный метод (Лаплас)
Математическая основа	Интеграл Фурье	Интеграл Лапласа
Комплексная переменная	\(\omega\) (чисто мнимая \((j\omega)\))	\(p = \sigma + j\omega\) (комплексная)
Учет начальных условий	Возможен, но вводится в исходные уравнения (как в формуле (1.3))	Вводится автоматически при дифференцировании (например, \((pU_C(p) — u_C(0))\))
Требования к сигналу	Сигнал должен быть абсолютно интегрируемым (\(\int \|f(t)\| dt < \infty\))	Менее строгие требования (сигнал должен расти не быстрее экспоненты)
Физическая интерпретация	Прямая: \(\omega\) — реальная угловая частота. АЧХ и ФЧХ имеют ясный физический смысл.	Абстрактная: \((p)\) — комплексная частота, не имеет прямой физической интерпретации.

Преимущества и недостатки спектрального метода

Преимущества

Физическая наглядность: Метод оперирует реальными частотами, АЧХ и ФЧХ, которые можно измерить экспериментально (например, с помощью генератора и осциллографа или анализатора спектра).
Работа с экспериментальными данными: Если передаточная функция \((H(j\omega))\) цепи неизвестна аналитически, но снята ее АЧХ и ФЧХ, спектральный метод позволяет рассчитать реакцию цепи.
Анализ искажений: Идеально подходит для качественной оценки того, как цепь исказит форму сигнала, путем сравнения спектра сигнала и АЧХ цепи.
Энергетический анализ: Теорема Рейли (рассмотрена ниже) напрямую связывает спектр с энергией сигнала.

Недостатки

Строгие ограничения: Неприменим к сигналам, которые не затухают со временем (например, к постоянному току или функции-ступеньке), в то время как метод Лапласа легко с ними справляется.
Сложность обратного преобразования: Нахождение оригинала \((f(t))\) по спектру \((S(j\omega))\) через интеграл Фурье часто оказывается математически более сложной задачей, чем взятие обратного преобразования Лапласа (например, по теореме разложения).

Частотные спектры типовых одиночных сигналов

Рассмотрим спектры двух наиболее распространенных импульсных сигналов.

1. Прямоугольный импульс

Определим спектр, амплитудно-частотный (АЧС) и фазо-частотный (ФЧС) спектры для прямоугольного импульса амплитудой \((A)\) и длительностью \((t_и)\) (рис. 1а).

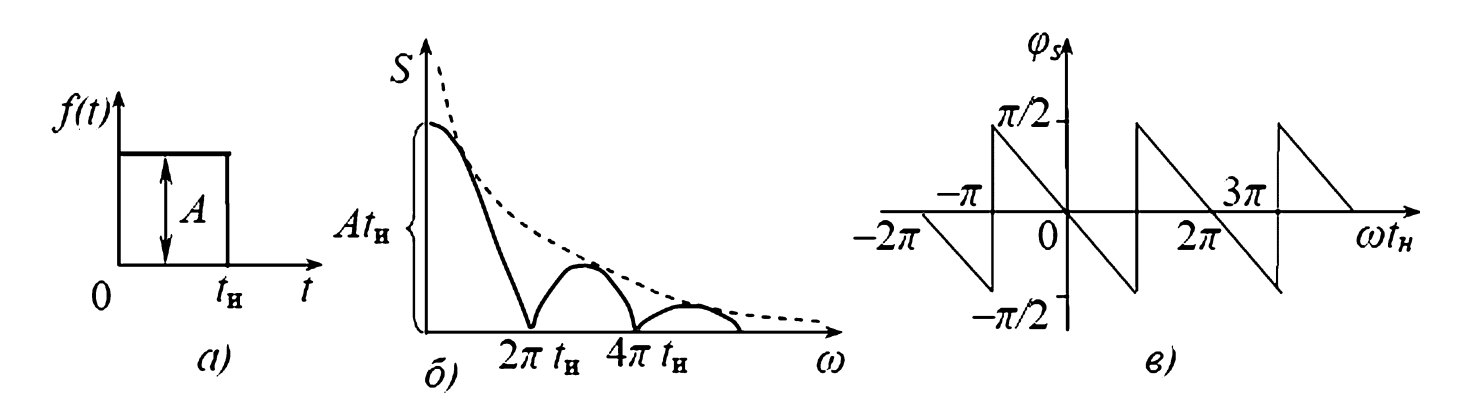
Рис. 1. Спектр прямоугольного импульса:

а — форма импульса; б — АЧС импульса; в — ФЧС импульса.

По общей формуле \((1.1)\), считая, что импульс начинается в \((t=0)\), определим спектр:

\[ S(j\omega) = \int_{0}^{t_и} A e^{-j\omega t} dt = A \left[ \frac{e^{-j\omega t}}{-j\omega} \right]_{0}^{t_и} = \frac{A}{-j\omega} (e^{-j\omega t_и} — 1) = \frac{A}{j\omega} (1 — e^{-j\omega t_и}) \]

Преобразуем это выражение, вынеся \((e^{-j\omega t_и / 2})\) за скобки, чтобы получить стандартную форму:

\[ S(j\omega) = \frac{A}{j\omega} e^{-j\omega t_и / 2} (e^{j\omega t_и / 2} — e^{-j\omega t_и / 2}) \]

Используя формулу Эйлера \((e^{jx} — e^{-jx} = 2j \sin(x))\), получаем:

\[ S(j\omega) = \frac{A}{j\omega} e^{-j\omega t_и / 2} (2j \sin(\frac{\omega t_и}{2})) = A t_и \frac{\sin(\frac{\omega t_и}{2})}{\frac{\omega t_и}{2}} e^{-j\omega t_и / 2} \]

Отсюда, амплитудно-частотный спектр (АЧС) \((S(\omega) = |S(j\omega)|)\) имеет вид (рис. 1б):

\[ S(\omega) = A t_и \left| \frac{\sin(\omega t_и / 2)}{\omega t_и / 2} \right| \]

Фазо-частотный спектр (ФЧС) \(\phi_S(\omega)\) определяется аргументом этого выражения. Он имеет линейную зависимость \((-\omega t_и / 2)\) с разрывами (скачками) на \(\pi\) в точках, где \(\sin(\omega t_и / 2)\) меняет знак (т.е. \(\omega t_и = 2\pi k\)) (рис. 1в).

2. Треугольный импульс

Для треугольного импульса (рис. 2а) с амплитудой \((A)\) и длительностью \((t_и)\) (основание треугольника), расчет спектра (путем интегрирования кусочно-заданной функции) дает следующий результат:

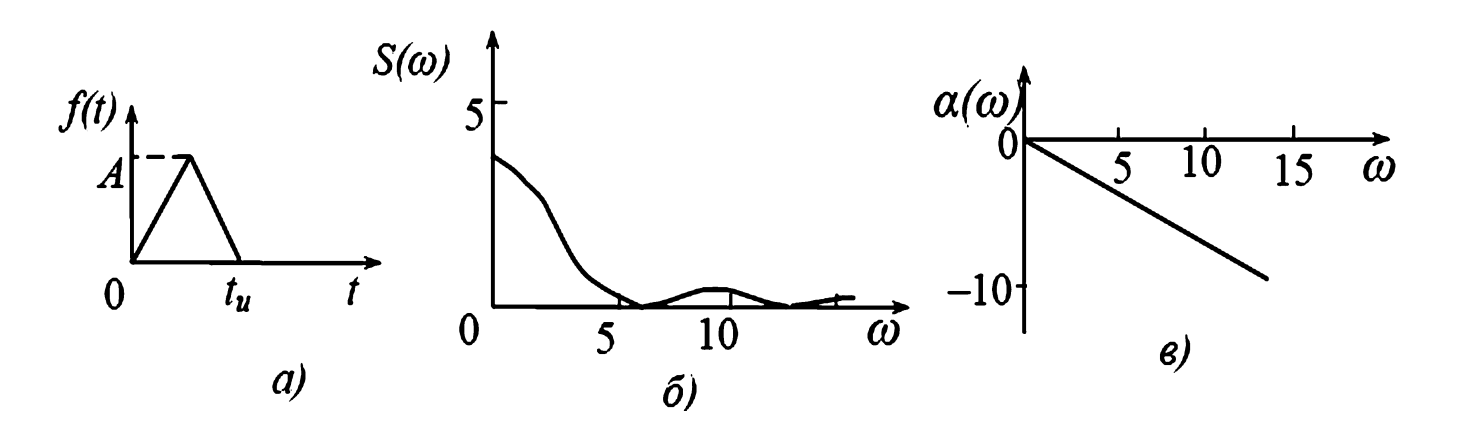
Рис. 2. Спектр треугольного импульса:

а — форма импульса; б — АЧС импульса; в — ФЧС импульса.

Спектральная плотность \((S(j\omega))\) имеет вид:

\[ S(j\omega) = \frac{A t_и^2}{2} \left[ \frac{\sin(\omega t_и / 4)}{\omega t_и / 4} \right]^2 e^{-j\omega t_и / 2} \]

Амплитудно-частотный спектр (АЧС) (рис. 2б):

\[ |S(j\omega)| = \frac{A t_и^2}{2} \left[ \frac{\sin(\omega t_и / 4)}{\omega t_и / 4} \right]^2 \]

Фазо-частотный спектр (ФЧС) (рис. 2в):

\[ \phi(\omega) = -\frac{\omega t_и}{2} \]

При подстановке в полученные выражения параметров треугольного импульса \((A = 4, t_и = 2)\) графики АЧС и ФЧС будут иметь вид, показанный на рис. 2 (б, в).

Принцип неопределенности: Сравнивая формы сигналов и их спектров, можно заметить важную закономерность: чем больше длительность сигнала \((t_и)\), тем уже его спектр, и наоборот, очень короткие импульсы (близкие к дельта-функции) имеют очень широкий (в пределе — бесконечный) спектр. Это проявление фундаментального принципа, связывающего длительность сигнала во времени \(\Delta t\) и ширину его спектра \(\Delta \omega\).

Теорема Рейли

Теорема Рейли (также известная как равенство Парсеваля для преобразования Фурье) устанавливает энергетическое соотношение между сигналом во временной и частотной областях. Для функции \((f(t))\), которая равна нулю при \((t < 0)\), теорему записывают следующим образом:

\[ \int_{0}^{\infty} f(t)^2 dt = \frac{1}{\pi} \int_{0}^{\infty} S(\omega)^2 d\omega \]

Здесь \((S(\omega))\) представляет собой модуль спектра \((S(j\omega))\) функции \((f(t))\).

Физический смысл: Если принять, что \((f(t))\) есть напряжение, приложенное к активному сопротивлению \((R = 1 \text{ Ом})\), то \((f(t)^2 / R = f(t)^2)\) — это мгновенная мощность. Тогда левая часть \(\int f(t)^2 dt\) представляет собой полную энергию \((W)\), выделяющуюся в этом сопротивлении за все время.

Таким образом, теорема Рейли гласит, что полная энергия сигнала, рассеиваемая в активном сопротивлении, равна интегралу от квадрата модуля спектра, деленному на \(\pi\). Величина \(\mathbf{S^2(\omega)}\) называется спектральной плотностью энергии сигнала, так как она показывает, как энергия сигнала распределена по частотам.

Применение спектрального метода

Спектральный метод используется для решения двух основных классов задач: прямого расчета переходных процессов и качественного анализа искажений.

Расчет переходных процессов

Расчет переходных процессов в обычных электрических цепях (с известными R, L, C) спектральным методом выполняют сравнительно редко, предпочитая использовать для этих целей операторный метод как более универсальный (особенно при наличии ненулевых начальных условий и не затухающих воздействий).

Однако применение спектрального метода становится вполне оправданным и эффективным в следующих случаях:

Когда частотная характеристика \((H(j\omega))\) исследуемой цепи (например, сложного фильтра или линии передачи) снята экспериментально, а ее аналитическое выражение \((H(p))\) неизвестно.
Когда входное воздействие имеет характер отдельных импульсов сложной формы, для которых спектр \((S(j\omega))\) известен или легко находится.

При этом, определив спектр выходной величины (например, \((U_2(j\omega))\)), ее оригинал \((u_2(t))\) определяют, используя обратное преобразование Фурье, часто с применением теоремы разложения.

Качественный анализ искажений в цепи

Частотные спектры сигналов позволяют проводить качественный анализ цепей в частотной области, то есть определить характер искажений сигнала при прохождении его через электрическую цепь без выполнения сложного обратного преобразования Фурье.

Простейшую оценку возможных искажений сигнала на выходе цепи можно получить, сопоставив амплитудно-частотный спектр (АЧС) входного сигнала с амплитудно-частотной характеристикой (АЧХ) функции передачи цепи.

Допустим, на вход цепи, функция передачи \((H(j\omega))\) которой известна, подается прямоугольный сигнал \((u_1(t))\). Требуется определить, каковы будут искажения сигнала \((u_2(t))\) при прохождении его через цепь.

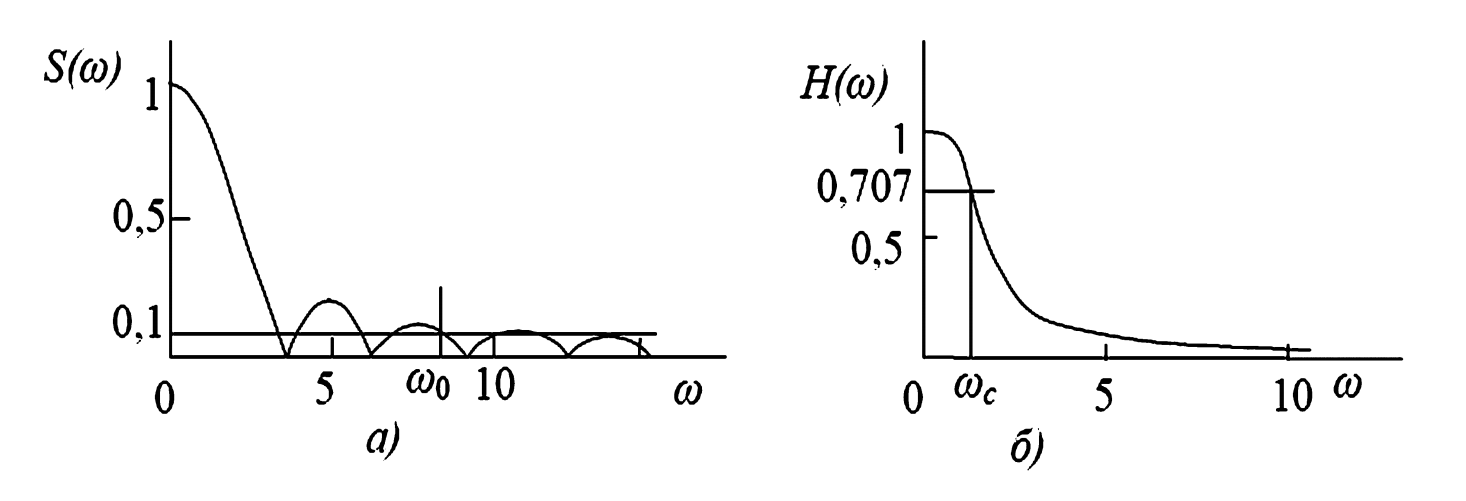
Рис. 3. Оценка искажений импульса при прохождении через электрическую цепь:

а — АЧС сигнала; б — АЧХ передаточной функции цепи.

Для качественной оценки искажений следует:

Построить АЧС входного сигнала \((S(\omega))\). Для прямоугольного сигнала он имеет вид, показанный на рис. 3а.
На графике АЧС определить эффективную ширину спектра \(\Delta\omega_{сигн}\). Практически ее можно определить, проведя линию, параллельно оси абсцисс на уровне 0,1 (10%) от максимального значения АЧС. Частота, на которой происходит последнее пересечение этой линии с графиком \((S(\omega))\), определит ширину спектра.
Построить АЧХ передаточной функции цепи \((H(\omega))\) (рис. 3б).
На графике АЧХ определить полосу пропускания цепи \(\Delta\omega_{цеп}\). Стандартно она определяется на уровне 0,707 (или \(-3 \text{ дБ}\)) от максимального значения. Диапазон частот, в котором график АЧХ лежит выше этой линии, является полосой пропускания.

Сопоставляя ширину спектра сигнала \(\Delta\omega_{сигн}\) с полосой пропускания цепи \(\Delta\omega_{цеп}\), можно дать качественную оценку искажениям сигнала на выходе цепи:

Если \(\Delta\omega_{сигн} < \Delta\omega_{цеп}\) (спектр сигнала уже полосы пропускания): цепь пропускает все значимые частотные компоненты сигнала. Искажения будут минимальными.
Если \(\Delta\omega_{сигн} \approx \Delta\omega_{цеп}\) (ширина спектра сравнима с полосой): цепь будет ослаблять и «срезать» высокочастотные компоненты спектра. Это приведет к заметным искажениям, в частности, к «затягиванию» фронтов импульса (увеличению времени нарастания и спада).
Если \(\Delta\omega_{сигн} > \Delta\omega_{цеп}\) (спектр сигнала намного шире полосы): цепь пропустит только малую, низкочастотную часть спектра. Искажения будут очень сильными, и форма сигнала на выходе может не иметь ничего общего с входной.

Интересные факты по теме

Фурье изучал тепло, а не электричество. Изначально Жозеф Фурье разработал свой математический аппарат в 1822 году для описания процессов распространения тепла в твердых телах, а не для анализа электрических сигналов.
Принцип неопределенности в сигналах. Замеченная закономерность «чем короче импульс, тем шире спектр» — это прямое следствие принципа неопределенности для сигналов. Невозможно создать сигнал, который был бы одновременно очень коротким во времени и очень узким по частоте.
«Звон» на изображениях. Эффект Гиббса, или «звон» (появление ложных контуров) на сжатых JPEG-изображениях или при цифровой обработке звука, является прямым следствием «среза» высокочастотных компонент спектра, аналогично тому, как электрическая цепь с узкой полосой пропускания искажает импульс.
Почему \((j)\), а не \((i)\)? В электротехнике и электронике для обозначения мнимой единицы \(\sqrt{-1}\) используется буква \((j)\), а не \((i)\), чтобы избежать путаницы с обозначением мгновенного значения тока \((i(t))\).
Основа цифрового мира. Быстрое преобразование Фурье (БПФ, или FFT) — это высокоэффективный алгоритм, разработанный в 1965 году для вычисления преобразования Фурье. Именно он лежит в основе почти всей современной цифровой обработки сигналов: от Wi-Fi и 4G/5G до сжатия музыки в MP3 и анализа медицинских снимков.

Часто задаваемые вопросы (FAQ)

1. Зачем нужен спектральный метод, если есть более универсальный операторный метод (Лапласа)?

Спектральный метод незаменим в двух областях. Во-первых, для анализа систем с неизвестной моделью: если у вас нет схемы (R, L, C), но вы можете измерить АЧХ и ФЧХ устройства (например, фильтра, усилителя или кабеля), вы можете предсказать его реакцию на любой импульс. Во-вторых, он дает физическую наглядность: он позволяет «увидеть», из каких частот состоит сигнал и как полоса пропускания цепи его исказит, что очень важно для качественного инженерного анализа.

2. В чем разница между АЧХ и АЧС?

Это ключевое различие:

АЧС (Амплитудно-частотный спектр) — это характеристика сигнала \((S(\omega))\). Она показывает, какую амплитуду имеет каждая частотная составляющая в самом сигнале.
АЧХ (Амплитудно-частотная характеристика) — это характеристика цепи \((H(\omega))\). Она показывает, как цепь изменяет (усиливает или ослабляет) амплитуду сигнала на каждой частоте.

Выходной спектр = (Входной АЧС) × (АЧХ цепи).

3. Почему короткий импульс имеет широкий спектр?

Короткий импульс (например, прямоугольный) имеет очень резкие фронты — напряжение меняется почти мгновенно. Чтобы математически описать такой резкий скачок, необходимо сложить вместе очень большое количество синусоид, включая синусоиды с очень высокой частотой. Чем резче скачок, тем более высокие частоты нужны для его «прорисовки». Медленный, плавный сигнал можно описать, используя в основном низкие частоты, поэтому его спектр будет узким.

4. Что физически означает теорема Рейли?

Теорема Рейли утверждает, что полная энергия сигнала одинакова, независимо от того, как мы ее считаем — во временной области (интегрируя квадрат напряжения по времени) или в частотной (интегрируя спектральную плотность энергии по частоте). Это фундаментальный закон сохранения энергии при переходе между двумя «представлениями» одного и того же сигнала.

5. Можно ли использовать метод Фурье для анализа цепи с постоянным током?

Строго говоря, нет. Постоянное напряжение \((U = const)\) не является абсолютно интегрируемой функцией (\(\int |U| dt \to \infty\)), и его классическое преобразование Фурье не существует. Для таких сигналов (а также для единичной ступеньки, синусоиды и т.д.) и был разработан операторный метод (преобразование Лапласа), который имеет лучшие свойства сходимости.

Заключение

Спектральный (частотный) метод, основанный на преобразовании Фурье, является мощным аналитическим инструментом для изучения поведения электрических цепей под воздействием непериодических и импульсных сигналов. Хотя для прямого расчета переходных процессов он часто уступает в удобстве операторному методу, его ценность заключается в непревзойденной наглядности и прямой связи с физически измеряемыми частотными характеристиками цепи — АЧХ и ФЧХ.

Возможность качественно оценить искажения сигнала путем простого сопоставления спектра сигнала и полосы пропускания цепи делает этот метод незаменимым для инженера. Понимание принципов спектрального анализа закладывает фундамент для изучения более сложных тем, включая теорию фильтрации и цифровую обработку сигналов (DSP), где преобразование Фурье является краеугольным камнем.

Нормативная база

При анализе и терминологии в области электрических цепей и сигналов рекомендуется опираться на следующие действующие стандарты:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». (Устанавливает основные термины, в том числе для электрических цепей).
ГОСТ 16465-70 «Сигналы радиотехнические измерительные. Термины и определения». (Определяет терминологию, связанную с параметрами сигналов, включая импульсные).

Список литературы

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Высшая школа, 2007.
Зевеке Г.В., Ионкин П.А., Нетушил А.В. Основы теории цепей. — М.: Энергоатомиздат, 1989.
Атабеков Г.И. Теоретические основы электротехники. Линейные электрические цепи. — СПб.: Лань, 2009.
Гоноровский И. С. Радиотехнические цепи и сигналы. — М.: Радио и связь, 1986.