Электрические моторы (двигатели). Мощность, вращение, момент, нагрузка электродвигателя.
Электрические моторы занимают настолько большую часть повседневной жизни, что мы редко задумываемся об этом. Когда мы включаем электрическую дрель, например, мы с уверенностью ожидаем возрастания оборотов до заданной скорости и не задаёмся вопросом, как она знает с какой скоростью работать, или как получается, что достаточное количество энергии, взятое из сети чтобы достигнуть заданной скорости, падает до очень низкого уровня непосредственно после разгона. Когда мы начинаем сверлить, она потребляет больше энергии, а когда мы заканчиваем сверлить, потребление от сети уменьшается автоматически без вмешательства с нашей стороны.
Безропотный двигатель, состоящий не более чем из конструкции медных обмоток и спрессованной стали, очевидно, представляется как умный преобразователь энергии, что является основанием для серьёзного изучения. Достигнув базового понимания работы двигателя, мы будем способны оценить его потенциал и ограничения, а также (в последующих главах) увидеть, как его замечательные характеристики могут быть улучшены с помощью добавления внешнего электронного управления.
Эта глава посвящена основополагающему механизму работы двигателя, поэтому читатели, которые уже знакомы с такими вопросами как магнитный поток, магнитные и электрические сети, момент и электродвижущая сила могут, вероятно, позволить себе пропустить её основную часть. В продолжение обсуждения, тем не менее, появляются несколько очень важных принципов и ориентиров. Они применяются ко всем типам двигателей и собраны в Части 1.8. Опыт показывает, что любой кто разобрался в этих базовых принципах будет хорошо подготовлен чтобы взвешивать все за и против различных типов двигателей, таким образом все читатели приглашаются познакомиться с ними до того как браться за другие части книги.
1.2 ВОЗНИКНОВЕНИЕ ВРАЩЕНИЯ
Почти все двигатели используют силу, которая возникает в токопроводящем проводе, помещённом в магнитное поле. Эта сила демонстрируется расположением бруска магнита около провода, проводящего ток (Фигура 1.1), но каждый, кто пытается провести эксперимент будет вероятно разочарован, обнаружив насколько слаба эта сила, и в удивлении усомнится в возможности такого мало обещающего эффекта быть использованным в изготовлении эффективных моторов.
Мы увидим, что необходимо очень сильное магнитное поле и много проводников, с как можно большим током, взаимодействующих с ним, чтобы получить максимальный эффект этого явления. Мы увидим также, что хотя магнитное поле (или «возбуждение») является важным для работы двигателя, оно работает только как катализатор, а вся механическая энергия выхода идёт от электрического питания проводников, на которых эта сила возникает. Позже выяснится, что в некоторых двигателях части ответственные за возбуждение и функции преобразования энергии ясны и самоочевидны. Например, в двигателях постоянного тока возбуждение, обеспечивается или постоянными магнитами или полем обмоток намотанных на явно выступающие полюса  неподвижной части, в то время как проводники, на которых возникает сила, располагаются на роторе и питаются током через щётки скольжения. Для многих моторов, тем не менее, нет чётко определённого разграничения между частями «возбуждения» и «преобразования энергии» двигателя, обычная стационарная обмотка служит двум целям. Несмотря на это, мы обнаружим, что определение и разделение функций возбуждения и преобразования энергии всегда помогают в понимании работы всех типов двигателей.
неподвижной части, в то время как проводники, на которых возникает сила, располагаются на роторе и питаются током через щётки скольжения. Для многих моторов, тем не менее, нет чётко определённого разграничения между частями «возбуждения» и «преобразования энергии» двигателя, обычная стационарная обмотка служит двум целям. Несмотря на это, мы обнаружим, что определение и разделение функций возбуждения и преобразования энергии всегда помогают в понимании работы всех типов двигателей.
Возвращаясь к вопросу силы в отдельном проводнике, прежде всего, посмотрим, что определяет величину и направление этой силы, до того как займёмся рассмотрением того как это явление используется для производства вращения. Чтобы понять, почему двигатели имеют такие формы, концепция магнитной цепи будет использована. Краткое введение в магнитное поле, магнитный поток и плотность потока приводятся для тех, кто не знаком с этими понятиями.
1.2.1 Магнитное поле и магнитный поток
Когда токопроводящий провод помещается в магнитное поле, то это порождает силу. Эксперимент показывает, что сила прямо зависит от тока в проводнике и силы магнитного поля, и что сила максимальна, когда магнитное поле перпендикулярно проводнику.

В эксперименте, показанном на Фигуре 1.1, источником магнитного поля является брусок магнита, который производит магнитное поле, изображённое на Фигуре 1.2.
Понятие «магнитное поле» окружающее магнит является абстрактной идеей помогающей восприятию загадочного феномена магнетизма:
это не только даёт нам возможность графически представить направление, но также позволяет делать количественную оценку «силы» магнетизма и, следовательно, позволяет предсказать различные эффекты созданные полем.
Пунктирными линиями на Фигуре 1.2 обозначаются линии магнитного потока или просто линии потока. Они показывают, как расположатся металлические опилки (или маленькие кусочки металла) в поле бруска магнита. Кусочки металла не имеют собственного магнитного поля, поэтому безразлично, каким концом к какому полюсу бруска магнита они повернутся.
Однако когда вы разместите в магнитном поле стрелку компаса (который сам является постоянным магнитом) то обнаружим, что он сам ориентируется, как показано на Фигуре 1.2. В верхней половине фигуры конец S ромбовидной стрелки компаса притягивается ближе к N полюсу магнита, в то время как в нижней части фигуры N конец компаса ищет S полюс магнита. Это наводит на мысль, что существует направленность линий потока, которая обозначается стрелками на линиях потока, за положительное направление принято направление от N полюса бруска магнита к S полюсу.
Глядя на эскиз Фигуры 1.2 можно предположить, что существует некий исток на верху бруска магнита, из которого линии потока выходят, прежде чем идти вниз. Но, если бы мы посмотрели на линии потока внутри магнита, то обнаружили бы их непрерывность без начала и конца. (На Фигуре 1.2 внутренние линии потока были опущены для простоты, но очень похожий образец поля создаётся круглой обмоткой провода проводящей постоянный ток. Посмотрите на Фигуру 1.6, на которой непрерывность линий потока очевидна.). Линии магнитного потока всегда формируют замкнутые пути, мы это увидим когда посмотрим на «магнитную цепь» и проведём параллель с электрической цепью, в которой ток также замкнут. (Конечно, должна быть «причина» возникновения магнитного потока, для постоянного магнита объяснения обычно на уровне токов атомов в материале магнита. К счастью, объяснения на таком физическом уровне не являются необходимыми для нашей цели.)
1.2.2 Плотность магнитного потока
Одновременно с указанием направления, график потока также передаёт информацию об интенсивности магнитного поля. Чтобы добиться этого мы вводим допущение, о том, что между любыми парами линий потока (в толще бумаги графика также) имеется одинаковое «количество» магнитного потока. Для некоторых людей нет трудностей с таким представлением, но для других представление количества чего-нибудь так абстрактно создаёт проблему. Однако кажется такой подход ясным или нет, удобство его практического применения к количественной оценке этого загадочного вещества названного нами – магнитный поток, несомненно, и ведёт к следующему очень важному понятию – плотность магнитного потока (B).
Когда линии потока располагаются ближе друг к другу, «труба» потока сжимается в меньшем пространстве, в сравнении с линиями этой же трубы в соседнем месте, где больше жизненного пространства. Плотность потока (B) есть просто поток в «трубе» (Ф) делённый на поперечное сечение площади (A) трубы, т.е.

![]()
Плотность потока есть векторная величина и поэтому часто пишется жирным шрифтом: его величина определяется выражением (1.1), а его направление есть результирующее направление линий потока в каждой точке. Около верхушки магнитного бруска на Фигуре 1.2, например, плотность потока будет больше (поскольку поток сжат в маленьком пространстве) и направлен вверх, в то время как в середине замкнутого кольца далеко от магнита плотность потока будет маленькой и направленной вниз.
Позже будет показано, как для того чтобы получить высокую плотность потока в двигателях, поток будет располагаться в основном внутри чётко определённой «магнитной цепи» сделанной из металла или стали, в этой цепи линии потока распределены равномерно, чтобы полностью использовать имеющееся пространство. В примере, показанном на Фигуре 1.3, площадь поперечного сечения по bb’ вдвое больше чем по aa’, а поток постоянный и поэтому плотность потока по bb’ есть половина от aa’.
Осталось определить единицу измерения для потока и плотности потока. В системе СИ единицей измерения магнитного потока является вебер (Wb). Если поток в один вебер распределен равномерно на площади 1м2 расположенной перпендикулярно потоку, то плотность потока будет один вебер на один квадратный метр (Wb/m2). Это определение было единицей измерения плотности магнитного потока на протяжении 40 лет, когда было решено назвать его – один тесла (T), в честь Никола Тесла, которому приписывается изобретение асинхронного двигателя. Широкое использование B (выраженной в теслах) на стадии конструирования всех типов электромагнитных аппаратов означает, что мы постоянно будем сталкиваться с важностью тесла; в тоже время надо отметить преимущество старой единицы измерения, которая ясно

показывала, что плотность потока есть поток, делённый на площадь.
В мире двигателей мы, к сожалению должны будем встречаться с потоками около нескольких милливеберов, а маленький брусок магнита, вероятно, создаёт только несколько микровеберов. В тоже время величина плотности потока обычно около 1T в большинстве моторов, это отражает тот факт, что хотя сам поток маленький, но распространяется он также в маленьком пространстве.
1.2.3 Сила на проводнике
Теперь вернёмся к возникновению силы на токопроводящем проводе, помещённом в магнитное поле, как было показано в опыте на Фигуре 1.1.
Направление силы показано на Фигуре 1.1: под прямыми углами к протекающему току и плотности магнитного потока. При плотности направленной горизонтально вправо и токе, вытекающем из листа, сила действует вертикально вверх. Если поле или ток направить в другую сторону, то направление действия силы изменится вниз, если поле и ток одновременно изменят направление, то направление действия силы останется без изменений вверх.
Экспериментально мы можем установить, что если увеличить вдвое ток или плотность потока, то сила увеличится вдвое, а если увеличить вдвое и ток и плотность потока, то сила увеличится в четыре раза. Но в каких единицах измеряется сила? Нам необходимо выразить силу в единицах её составляющих: тока и плотности магнитного потока, если мы работаем в системе СИ всё вполне определённо.
Сила на проводе длиной l проводящем ток I помещённом в однородном поле с плотностью магнитного потока B по всей его длине определяется простой формулой
![]()
где F в ньютонах, B в теслах, I в амперах, а l в метрах. Это превосходно простая формула, и вероятно для некоторых читателей будет сюрпризом отсутствие коэффициентов пропорциональности в выражении 1.2. Эта простота не случайна, а следует из того факта, что единица тока (ампер) в действительности определяется в терминах силы. Строго говоря, выражение 1.2 применяется только, когда ток перпендикулярен полю. Если это условие не выполняется, сила на проводнике будет меньше; в крайнем случае, когда ток течёт в том же направлении что и поле сила уменьшится до нуля. Поскольку каждый разумный конструктор двигателей знает это, то можно предположить в дальнейших обсуждениях, что B и I всегда перпендикулярны друг другу. В оставшейся части книги плотность потока и ток взаимно перпендикулярны, поэтому, хотя B вектор (должен обозначаться жирным шрифтом) мы можем опустить это обозначение, поскольку направление неявно задано и нас интересует только величина.
Причина очень маленькой силы в эксперименте с бруском магнита объясняется выражением 1.2. Чтобы получить большую силу мы должны иметь большую плотность потока и много тока. Плотность потока на концах бруска магнита маленькая, вероятно 0.1 тесла, поэтому провод, по которому течёт ток 1 ампер, будет создавать силу только 0.1 N/m (примерно 100 грамм веса). А поскольку плотность потока ограничена в пространстве 1см поперечного сечения магнита, реальная сила на проводе будет только 1 грамм. Такую величину трудно обнаружить и как-то использовать в нормальном моторе. Как же получают больше силы?
Первый шаг состоит в том, чтобы увеличить до максимально возможного плотность потока. Это достигается конструированием «хорошей» магнитной сети, как обсуждается далее. Во-вторых, как можно больше проводников должно быть размещено там, где существует магнитное поле, и по каждому проводнику должен течь ток максимально возможный величины, только чтобы не нагревать его до опасной температуры. Таким путем могут быть получены впечатляющие силы от устройств небольших размеров, каждый, кто попытается затормозить патрон дрели может убедиться в этом.
1.3 МАГНИТНЫЕ ЦЕПИ
До сих пор мы полагали, что источником магнитного поля является магнит. Это удобная отправная точка, поскольку все из нас знакомы с магнитами, даже если это знакомство в виде двери холодильника. Но в большинстве моторов рабочее магнитное поле создаётся обмоткой провода с протекающим по ней током. Поэтому будет уместным, если мы потратим некоторое время и рассмотрим, как должны быть устроены обмотки и связанное с ними железо «магнитной цепи», чтобы произвести сильное магнитное поле, способное взаимодействуя с токопроводящими проводниками создать силу, а значит и вращение.

Прежде всего, посмотрим на простейшее магнитное поле окружающее изолированный длинный и прямой провод, проводящий постоянный ток (Фигура 1.4). (На этой фигуре символ + обозначает ток, протекающий в направлении от нас в страницу, а символ точка обозначает направление от страницы к нам: эти символы можно запомнить с помощью образа стрелы, где + это вид сзади оперения, а точка это наконечник). Линии потока образуют круги с центром на проводе, чем ближе к проводу, тем сильнее поле. Можно предположить, что сила поля прямо пропорциональна току. Правило для определения направления поля гласит, что положительным будет направление закручивания буравчика по току.
Фигура 1.4 несколько упрощена, поскольку ток может течь только в замкнутой цепи, поэтому обратный путь тока также предполагается. Если мы изобразим рядом прямой и обратный путь тока, то поле получится наложением двух полей от прямого и обратного тока как показано на Фигуре 1.5.
Отметим, как поле увеличилось в области между проводниками и уменьшилось снаружи. Хотя Фигура 1.5, обозначает только пару бесконечно длинных прямых проводников, не будет трудно усвоить, что виток провода прямоугольной или круглой формы имеет такое же поле как на Фигуре 1.5. Это позволит нам нарисовать картину поля,

создаваемую в воздухе обмотками двигателей, обычно обмотки имеют много витков как показано на Фигуре 1.6.
Сама обмотка показана слева на Фигуре 1.6, тогда как изображение потока созданного ею справа.

Каждый виток обмотки создаёт элемент поля и когда все элементы складываются, мы видим, что поле внутри обмотки значительно увеличилось, и что замкнутый магнитный путь очень похож на то, что мы видели вокруг бруска магнита ранее. Окружающий воздух является однородным пространством для распространения потока, поэтому поток, выходя из обмотки, свободно распространяется во всём окружающем пространстве. Напомним, что между каждой парой линий потока имеется одинаковое количество потока, мы видим, как линии расходятся, покидая ограниченное пространство обмотки, плотность потока значительно меньше снаружи обмотки: например, если расстояние “b” в четыре раза больше чем “a” плотность потока Bb будет четверть от Ba.
Хотя плотность потока внутри обмотки выше, чем снаружи мы видим, что это всё равно не достаточно для использования в двигателе. Прежде всего, нам нужно увеличить плотность потока, а это означает концентрацию потока, предотвращение его распространения в окружающем пространстве.
1.3.1 Магнитодвижущая сила (MMF)
Один из способов увеличить плотность потока это увеличить ток в обмотке или добавить больше витков. Мы увидим, что если удвоить ток или число витков, то удвоится поток и плотность повсюду. Способность обмотки создавать поток оценивается по её магнитодвижущей силе (MMF). MMF обмотки есть просто произведение количества витков (N) и тока (I), и поэтому выражается в ампер-витках. Нужная MMF может быть получена большим количеством витков тонкого провода, проводящего малый ток или малым количеством витков толстого провода, проводящего большой ток: если произведение NI постоянно и MMF, следовательно, тоже.
1.3.2 Аналогия электрической цепи
Мы увидели, что полученный магнитный поток пропорционален возбуждающей MMF. Этот вывод аналогичен электрической цепи, где протекающий ток (амперы) пропорционален EMF (электродвижущей силе в вольтах) возбуждающей его.
В электрической цепи отношения между током и EMF определяются законом Ома

Для данной EMF (вольты) ток зависит от сопротивления цепи, поэтому, чтобы получить больший ток, сопротивление цепи должно быть уменьшено.
Мы можем использовать как эквивалент «магнитный закон Ома», введя понятие магнитного сопротивления (R). Магнитное сопротивление является мерой того насколько трудно магнитному потоку замкнуть свою цепь, точно также как сопротивление показывает насколько большое противодействие току в электрической сети. Тогда магнитный закон Ома

Из формулы 1.4 мы видим, что для увеличения потока при заданной MMF нам необходимо уменьшить сопротивление магнитной цепи. В случае нашего примера (Фигура 1.6), это означает, что мы должны заменить как можно больше путь по воздуху (он является плохим магнитным материалом и создаёт большое сопротивление) другим путём с хорошим магнитным материалом, уменьшая магнитное сопротивление и, следовательно, увеличивая поток, при заданной MMF.
Материал, который мы выбираем это высококачественная магнитная сталь, исторически используется название «железо». Это приводит к ряду впечатляющих и желательных выгод как показано на Фигуре 1.7. Во-первых, магнитное сопротивление железных путей значительно меньше, чем воздушных, которые они заменили, поэтому общий поток созданный той же MMF значительно больше. (Короче говоря, если MMF и поперечные сечения катушек на Фигурах 1.6 и 1.7 одинаковы, гораздо больше линий потока должно быть показано на Фигуре 1.7, чем на Фигуре

1.6, но для простоты это не делается.) Во-вторых, почти весь поток сосредоточен внутри железа, а не в окружающем воздухе. Поэтому мы можем придавать такую форму железным частям магнитной цепи, на Фигуре 1.7, которая необходима потоку. И последнее, мы видим, что внутри железа, плотность потока равномерно распределена по поперечному сечению, поскольку сопротивление так мало, что нет заметной тенденции к скоплению потока не какой-то стороне.
Перед тем как мы перейдем к вопросу воздушного зазора, мы должны усвоить ответ на часто задаваемый вопрос: имеет ли значение, как плотно к железу намотана обмотка, а в случае с многослойной обмоткой: одинаково ли эффективны обмотки внутреннего и наружного слоёв. Ответ, к счастью, такой, что для MMF важно только количество витков и ток в них, и не важно, насколько плотно они намотаны. Конечно, имеет смысл наматывать обмотку плотнее, поскольку это уменьшает её сопротивление (и, следовательно, уменьшает потери тепла), а также облегчает отвод тепла на корпус двигателя.
1.3.3 Воздушный зазор
В двигателях мы планируем использовать поток с высокой плотностью, чтобы создать силу на токопроводящих проводах. Мы увидели, как создать поток большой плотности в железных частях магнитной цепи, но, конечно, физически невозможно разместить токопроводящие провода внутри железа. Поэтому мы предусматриваем воздушный зазор в магнитной цепи как показано на Фигуре 1.7. Вскоре мы увидим как провода, на которых возникает сила, будут размещаться в области воздушного зазора.
Если воздушный зазор относительно маленький, что справедливо для двигателей, то мы обнаружим, что поток перепрыгивает через воздушный зазор как показано на Фигуре 1.7, с очень маленькой тенденцией к разбуханию в окружающем воздухе. Основная часть линий потока идёт прямо через зазор, плотность потока в воздушном зазоре имеет такую же большую величину, как и в железе.
В большинстве магнитных цепей состоящих из железных частей и одного или нескольких воздушных зазоров, магнитное сопротивление железных частей значительно меньше чем зазоров. На первый взгляд это может показаться странным, поскольку расстояние зазора значительно меньше, чем остального пути в железе. Тот факт, что воздушный зазор определяет магнитное сопротивление, просто показывает, насколько плохим проводником для потока является воздух в сравнении с железом. Для сравнения, если посчитать магнитное сопротивление двух участков цепи одинаковой длины и поперечного сечения из воздуха и железа, то магнитное сопротивление воздуха будет примерно в 1000 раз больше чем железа. (Расчёт магнитного сопротивления будет обсуждаться в Части 1.3.4.)
Возвращаясь к аналогии с электрической цепью, роль железных частей магнитной цепи можно уподобить медным проводам электрической цепи. Обе оказывают маленькое сопротивление потоку (такое, что незначительная часть движущей силы (MMF или EMF) тратится на транспортировку потока туда, где он используется), и обе могут быть сконфигурированы так чтобы направить поток к месту назначения. Тем не менее, имеется одно важное отличие, В электрической сети ток не течёт, пока цепь не замкнута. После замыкания весь ток течёт внутри электрических проводов. В магнитной цепи поток может течь (в окружающем воздухе) даже до того как железо установлено. И хотя впоследствии поток найдёт лёгкий путь через железо, некоторая часть будет рассеиваться в воздухе, как показано на Фигуре 1.7. Мы не будем рассматривать здесь утечку потока, хотя иногда это важно, как будет показано позже.
1.3.4 Магнитное сопротивление и плотность потока в воздушном зазоре
Если пренебречь сопротивлением железных частей магнитной цепи, то будет легко оценить плотность потока в воздушном зазоре. Поскольку железные части в действительности «идеальные проводники» потока, источник MMF (NI) не затрачивается на прохождение потока через железные части, а весь расходуется, чтобы протолкнуть поток через воздушный зазор. Ситуация изображённая на Фигуре 1.7 увеличена на Фигуре 1.8, где MMF величиной NI непосредственно прикладывается к воздушному зазору длинной g.

Чтобы определить величину потока пересекающего зазор нам нужно знать его магнитное сопротивление. Можно предположить, что сопротивление любой части магнитной цепи зависит от её размеров и магнитных свойств, поэтому сопротивление прямоугольной призмы воздуха с поперечным сечением A и длиной g как показано на Фигуре 1.8 определяется формулой

где µ0 есть так называемая «основная магнитная постоянная» или «магнитная проницаемость пустого места». Строго говоря, как следует из названия, µ0 определяет магнитные свойства вакуума, но для всех инженерных расчётов коэффициент проницаемости воздуха тоже µ0 . Величина основной магнитной постоянной (µ0) в системе СИ есть
4π х 10-7 H/m; трудно найти более странное обозначение для единицы измерения магнитного сопротивления.
Попутно заметим, что если мы хотим включить сопротивление железной части магнитной цепи в наши расчёты, то её сопротивление даётся формулой

и нам надо будет добавить это сопротивление к сопротивлению воздушного зазора, чтобы получить общее сопротивление. Тем не менее, поскольку проводимость железа (µfe) гораздо больше µ0, то сопротивление железа будет значительно меньше чем сопротивление воздушного зазора, несмотря на то, что длина пути существенно больше чем путь (g ) по воздуху.
Выражение 1.5 демонстрирует ожидаемый результат, о том, что удвоение воздушного зазора удваивает сопротивление (поскольку поток должен дважды пересечь зазор), в то время как удвоение поперечного сечения уменьшало бы сопротивление вдвое (поскольку поток имел бы два параллельных пути). Чтобы рассчитать поток, мы используем магнитный закон Ома (Формула 1.4), которая дает

Обычно мы интересуемся плотностью потока в зазоре, а не общим потоком поэтому, используя формулу 1.1, имеем

Формула 1.7 приятно проста, пользуясь этой формулой, мы можем вычислить плотность потока в воздушном зазоре, если известны MMF обмотки (NI) и длина зазора (g). Нам не нужно знать ни подробности конструкции обмотки, если мы знаем количество витков и ток, ни поперечное сечение магнитной цепи, чтобы получить плотность потока (тем не менее, мы можем узнать общий поток по формуле 1.6).
Например, предположим, что намагничивающая обмотка имеет 250 витков, протекающий ток 2 А, а зазор 1 мм. Плотность потока вычисляется как

(мы, конечно, могли бы получить тот же результат, используя мощную обмотку с 50 витками и током 50 А, или какую-нибудь другую комбинацию витков и тока, дающую MMF 500 ампер-витков).
Если поперечное сечение железа одинаково по всей цепи, плотность потока была бы 0.63 Т везде. Иногда, как уже упоминалось, поперечное сечение железа уменьшается в местах далёких от воздушного зазора, как показано, например, на Фигуре 1.3. Поскольку поток сжимается в узких местах, плотность потока выше, но как видно на Фигуре 1.3 плотность потока в воздушном зазоре и смежных полюсах опять становится 0.63 Т, тогда как в сечении aa’ (где поперечное сечение составляет только половину от сечения около воздушного зазора) плотность потока будет 2 х 0.63 = 1.26 Т.
1.3.5 Насыщение
Будет резонным задать вопрос, а где находится предел плотности потока, при котором железо может работать. Мы можем предвидеть, что должен быть предел, и ещё, что возможно втолкнуть поток в бесконечно маленькое поперечное сечение, такое, что не используется на практике. Предел существует, хотя и не очень чётко определённый.
Ранее мы упоминали, что железо почти не имеет сопротивления, по крайней мере, в сравнении с воздухом. К несчастью такое сравнение справедливо только до 1.6 – 1.8 Т в зависимости от железа. Если мы попытаемся использовать железо при большей плотности потока, оно начнёт демонстрировать значительное сопротивление, и не ведёт себя более как идеальный проводник потока. При таких больших плотностях потока значительная часть источника MMF расходуется на прохождение потока через железо. Такое положение не желательно, поскольку меньше MMF остаётся для прохождения потока через воздушный зазор. Таким образом, точно также как мы не рекомендовали использовать питающую цепь, с большим сопротивлением ведущую к перегрузке электрической цепи, мы должны избегать перегрузки железных частей в магнитной цепи.
Появление значительного сопротивления с ростом плотности потока иллюстрируется качественно на Фигуре 1.9.

Когда сопротивление становится заметным, говорят, что железо «насыщается». Термин подходящий потому, что если продолжить увеличивать MMF или уменьшать сечение железа, то, в конце концов, мы достигнем почти постоянной плотности потока обычно около 2 Т. Чтобы избежать нежелательного эффекта насыщения, размеры железных частей магнитной цепи обычно выбираются так, чтобы плотность потока не достигала 1.5 Т. На этом уровне плотности потока сопротивление железных частей будет небольшим в сравнении с воздушным зазором.
1.3.6 Магнитные цепи в двигателях
Читатель может удивиться, почему такое большое внимание сконцентрировано на С-образных магнитных цепях с зазором, пока не обнаружит схожесть с магнитными цепями двигателей. Сейчас мы увидим, что не требуется никаких новых идей для маленького шага от С-образных магнитных цепей с зазором к магнитным цепям двигателей.
Эволюция от С-образной геометрии к двигательной геометрии показана на Фигуре 1.10, которая сама по себе всё объясняет на примере двигателя постоянного тока.
Отметим, что на первом этапе эволюции (Фигура 1.10 слева) исходный зазор длиной g разделяется на два зазора длиной g /2, отражая необходимость для ротора вращаться. В тоже время одна

намагничивающая обмотка разделяется на две симметричных. (Перемещение намагничивающей катушки в другое место магнитной цепи, конечно, не создаёт проблемы, точно также как батарея может размещаться где угодно в электрической цепи). На следующем шаге (Фигура 1.10 в центре) одинарный магнитный контур разделяется на два параллельных контура с поперечным сечением в половину от исходного, каждый контур проводит половину исходного потока. Окончательно (Фигура 1.10 справа), контуры потоков и полюсов изгибаются, чтобы подходить для ротора. Катушка теперь имеет несколько слоёв, чтобы разместиться в имеющемся пространстве, однако, как говорилось ранее, это не создаёт негативного эффекта на MMF. Воздушный зазор по прежнему маленький и магнитный поток пересекает его по радиусу к ротору.
1.4 СОЗДАНИЕ МОМЕНТА
Сконструировав магнитную цепь, чтобы создать высокую плотность потока под полюсами, мы хотим получить максимальную пользу от этого. Для этого нам надо разместить на роторе ряд проводников, как показано на Фигуре 1.11, и обеспечить положительный ток (в поверхность страницы) под N-полюсом (на верху Фигуры 1.11) и отрицательный ток под S-полюсом. Тангенциальная электромагнитная сила (B Il ) (смотри формулу 1.2) созданная на всех положительных проводниках, будет направлена влево, а на отрицательных вправо. Пара сил или момент создаются на роторе, что приведёт к вращению.
(Наблюдательный читатель, заметивший отсутствие тока в некоторых проводниках найдёт объяснение позже в Главе 3.)
В этом месте нам надо прерваться и задать три вопроса, которые часто возникают при рассмотрении этих идей. Первый это почему мы не упоминаем магнитное поле наведённое током, протекающим по проводникам ротора. Без сомнения, они также будут создавать магнитное поле, которое вероятно будет пересекаться с основным в воздушном зазоре, можно предположить, что в этом случае, формула для вычисления силы на проводниках не верна.
Ответ на этот чувствительный вопрос в том, что поле, созданное протекающим в проводниках ротора током, определённо будет искажать основное поле (т.е. поле, созданное при отсутствии тока в проводниках ротора). Но в большинстве двигателей, сила на проводнике может

рассчитываться правильно на основании действующего тока и «оригинального» поля. Это не только удача с точки зрения вычисления силы, но также логично. Например, на Фигуре 1.1 мы не ожидаем какой-либо силы на токопроводящем проводе, если нет внешнего поля, хотя поле будет создаваться током, протекающим по проводнику (с одной стороны проводника вверх, с другой вниз). Поэтому кажется логичным вывод, что сила создаётся только при наличии внешнего поля, любая сила есть следствие единственно внешнего поля.
Второй вопрос возникает, когда мы задумываемся о законе действия и противодействия. Когда имеется момент на роторе, вероятно, имеется такой же, но противоположно направленный момент на статоре; мы можем удивиться, поскольку механизм создания момента на статоре точно такой же, как на роторе. Ответ на второй вопрос будет да; всегда имеется эквивалентный и противоположно направленный момент на статоре, вот почему обычно важно надёжно закреплять двигатель. В некоторых двигателях (например, асинхронных) легко видеть, что момент создаётся на статоре взаимодействием плотности потока в воздушном зазоре и токами статора, точно также как плотность потока взаимодействует с токами ротора, чтобы создать момент на роторе. Для других двигателей, (например для рассматриваемых двигателей постоянного тока) нет простого физического объяснения, которое может определить момент на статоре но, тем не менее, он равен и противоположно направлен моменту ротора.
Последний вопрос относится к сходству между устройством, показанным на Фигуре 1.10, и видом поля созданного, например, электромагнитом чтобы поднимать корпуса автомобилей на свалке. Из этого примера мы знаем, какая большая сила притяжения может быть создана подъёмным магнитом, можем ли мы ожидать такую же большую силу между полюсом статора и железным корпусом ротора? И если да, то, что может предотвратить притягивание ротора к статору?
Ответ опять положительный, поскольку действительно имеется радиально направленная сила, вызванная магнитным притяжением, точно также как в подъёмном магните или реле, хотя механизм, согласно которому магнитное поле вызывает притяжение, проникая в железо или сталь, полностью отличается от «B Il » силы, которую мы рассматривали до сих пор.
Оказывается, что сила притяжения, приходящаяся на единицу площади сечения полюса, пропорциональна квадрату радиальной плотности потока, при типичных плотностях потока в воздушном зазоре двигателей до 1 Т, сила на единицу площади составляет около 40 Н/cм2. Отсюда следует, что радиальная сила может быть очень большой: например сила притяжения маленького полюса 5 х 10 см составляет 2000Н или около 200 Кг. Эта сила никак не участвует в создании момента, а является просто не желательным побочным продуктом «B Il » механизма, который мы используем для создания тангенциальной силы на проводниках ротора.
В большинстве двигателей радиальная магнитная сила под каждым полюсом в действительности значительно больше, чем тангенциальная электромагнитная сила на проводниках ротора, и как предполагает вопрос, это приводит к притягиванию ротора к полюсу. Однако большинство двигателей сконструированы с парным количеством полюсов равномерно расположенных вокруг ротора, а плотность потока одинакова для каждого полюса, поэтому (по крайней мере, в теории) результирующая сила, действующая на ротор равна нулю. На практике, даже маленький эксцентриситет будет создавать более сильное поле под полюсом с меньшим воздушным зазором, что создаст рост несбалансированного притяжения, и как следствие шум при работе, а также быстрый износ подшипников.
1.4.1 Величина момента
Возвращаясь к первоначальному обсуждению, сила на каждом проводнике определяется формулой 1.2, из которой следует, что результирующая тангенциальная сила F зависит от плотности потока созданного обмотками возбуждения, количества проводников на роторе, тока в каждом из них и длины ротора. Результирующий момент или пара сил (Т) зависит от радиуса ротора (r), определяется формулой
![]()
Мы продолжим это рассмотрение далее в Части 1.5, после того как убедимся в замечательных выгодах размещения проводников в пазах.
1.4.2 Преимущество пазов
Если бы проводники были размещены на поверхности ротора как на Фигуре 1.11, то высота воздушного зазора должна была бы быть, по крайней мере, равной диаметру провода, а проводники должны были бы быть закреплены на роторе чтобы передать ему вращающую силу. Первые двигатели были сделаны таким образом с проводниками, привязанными к ротору верёвкой или лентой.
К несчастью в результате воздушный зазор имел большое магнитное сопротивление и много витков обмоток с большим током были необходимы, чтобы создать достаточную плотность тока в воздушном зазоре. Это означает, что обмотка возбуждения становится очень громоздкой и потребляет много энергии. Ранним изобретателям (19 век) пришла идея частично опустить проводники ротора в углубления, сделанные на роторе параллельно валу, целю было уменьшить воздушный зазор, чтобы обмотка возбуждения стала меньше. Это сработало исключительно хорошо, поскольку было создано лучшее место для проводников и передачи от них силы ротору. Вскоре проводники начали утапливать в равномерно глубокие пазы и, в конце концов (смотри Фигуру 1.12) они больше не выступают над поверхностью ротора и величина воздушного зазора может устанавливаться исходя из требований механики. Новые «пазовые» двигатели работали очень хорошо и их прагматичные производители не беспокоились по поводу бесконечной шумихи скептичных теоретиков.

Теоретики того времени приняли погружение проводников в пазы и как следствие маленький воздушный зазор, но заметили, что как видно из Фигуры 1.12, почти весь поток теперь проходит через зубья с маленьким магнитным сопротивлением, оставляя проводники для очень маленького потока в пазах. Они уверенно заявляли, что будет создаваться маленькая (или вообще не будет) «B Il » сила на проводниках, поскольку теперь они доступны только для очень маленькой плотности потока.
Скептики были правы в то, что поток действительно должен течь через зуб; но не отрицалось и то, что двигатели с пазовым ротором создают такой же момент, как и с проводниками в воздушном зазоре при условии, что средняя плотность потока на поверхности ротора была одинакова. Не слишком ли хорошее объяснение чтобы быть правдой?
Поиск объяснения занимал умы ведущих мыслителей в течении долгого времени после того как пазы стали нормой, и в конце концов стало возможным теоретически доказать, что в целом, сила остаётся такой же как если бы проводники были в потоке, однако теперь почти вся тангенциальная сила воздействовала на зуб, а не на сам проводник.
Это замечательные новости. Уложив проводники в пазы, мы одновременно сделали возможным уменьшение сопротивления магнитной цепи, и перенесли воздействие силы непосредственно с проводников на стенки зуба, которые надёжны и лучше приспособлены для передачи результирующего момента на вал. Другая выгода в том, что изоляции вокруг проводников не надо больше передавать тангенциальную силу на ротор, и таким образом, требования к её механическим характеристикам менее критичны. Как-нибудь можно провести опыт по определению полезного действия в каком-либо значимом направлении.
Имеется ряд затруднений, тем не менее. Чтобы максимизировать момент мы будем желать как можно больший ток в проводниках ротора. Естественно мы будем работать с медью при максимально возможной плотности тока (обычно между 2 и 8 A/мм2), также мы будем хотеть увеличить поперечное сечение паза, чтобы разместить в нём максимально возможное количество меди. Это заставит нас сделать широкий паз и, следовательно, узкий зуб. Но напомним, что поток должен идти радиально вниз к зубу, поэтому если мы сделаем зуб узким, то железо зуба будет насыщаться, что приведёт к плохой магнитной цепи. Имеется возможность увеличить глубину паза, но мы не можем идти слишком близко к центру ротора, поскольку железо ротора, проводя поток от одного полюса к другому, становится слишком облегчённым, и также будет насыщаться.
В следующей части мы рассмотрим, что определяет момент при заданном размере ротора, также посмотрим, как скорость играет ключевую роль в определении выходной мощности.
1.5 СРЕДНИЕ НАГРУЗКИ И СРЕДНАЯ МОЩНОСТЬ
1.5.1 Средние нагрузки
Компромисс при конструировании в области воздушного зазора неизбежен, конструктор постоянно должен применять свои знания, чтобы достигнуть наилучшего баланса между противоречивыми требованиями в пространстве потока (радиальном) и тока (аксиальном).
Как часто бывает при конструировании, направление дизайна проясняется как компромисс между конкретными размерами и типами двигателей, конструктор двигателей обычно работает в терминах двух параметров: средней магнитной нагрузки и средней электрической нагрузки. Эти параметры непосредственно определяют выход двигателя, как мы сейчас увидим.

Средняя магнитная нагрузка (![]() ) есть средная величина радиальной плотности потока, проходящей через всю цилиндрическую поверхность ротора. По причине наличия пазов, средная плотность потока всегда меньше плотности потока в зубе, но для расчёта магнитной нагрузки мы рисуем ротор гладким и расчитываем средную плотность потока деля общий радиальный поток от каждого «полюса» на поверхность под ним.
) есть средная величина радиальной плотности потока, проходящей через всю цилиндрическую поверхность ротора. По причине наличия пазов, средная плотность потока всегда меньше плотности потока в зубе, но для расчёта магнитной нагрузки мы рисуем ротор гладким и расчитываем средную плотность потока деля общий радиальный поток от каждого «полюса» на поверхность под ним.
Средняя электрическая нагрузка ( обычно обозначается символом (![]() ), измеряемая в Амперах) есть аксиальный ток на метр длины окружности ротора. На пазовом роторе аксиальный ток концентрируется в проводниках внутри каждого зуба, но для расчёта
), измеряемая в Амперах) есть аксиальный ток на метр длины окружности ротора. На пазовом роторе аксиальный ток концентрируется в проводниках внутри каждого зуба, но для расчёта ![]() мы изображаем общий ток равномерно распределённым по длине окружности (в манере аналогичной представленной на Фигуре 1.12, но с отдельными проводниками, обозначенными под каждым полюсом с равномерно распределённым «токовым графиком»). Например, если под полюсом с дугой шириной 10 см имеется пять пазов, в каждом из которых протекает ток 40 А, электрическая нагрузка будет:
мы изображаем общий ток равномерно распределённым по длине окружности (в манере аналогичной представленной на Фигуре 1.12, но с отдельными проводниками, обозначенными под каждым полюсом с равномерно распределённым «токовым графиком»). Например, если под полюсом с дугой шириной 10 см имеется пять пазов, в каждом из которых протекает ток 40 А, электрическая нагрузка будет:
![]()
Много факторов влияет на величины, которые могут использоваться при конструировании двигателя, но по существу средние магнитная и электрическая нагрузки ограничиваются свойствами материалов (железа для потока и меди для тока), а также системой охлаждения используемой для отвода тепловых потерь.
Средняя магнитная нагрузка не сильно отличается для разных двигателей, поскольку условия насыщения для большинства сталей аналогичны. С другой стороны довольно большие вариации наблюдаются для средней электрической нагрузки связанные с типом используемого охлаждения.
Несмотря на низкое сопротивление медных проводников, протекающий ток генерирует тепло, поэтому ток должен быть ограничен до величины, при которой изоляция не разрушается под действием чрезмерной температуры. Чем эффективнее охлаждающая система, тем выше может быть электрическая нагрузка. Например, если двигатель полностью закрыт и не имеет внутреннего вентилятора, плотность тока в меди должна быть гораздо меньше, чем для аналогичного двигателя с вентилятором, обеспечивающим постоянный поток вентилируемого воздуха. Аналогично, обмотки возбуждения полностью импрегнированные лаком могут работать более напряжённо, чем те, которые окружены воздухом, так как твёрдое тело оболочки лака создаёт гораздо лучший термальный путь, вдоль которого тепло может перетекать в тело статора. Габаритный размер также играет свою роль в определении допустимой электрической нагрузки, в общем, чем больше размер, тем больше нагрузка.
На практике, важный момент, который надо иметь в виду состоит в том, что во всех случаях, когда не используется какая-нибудь экзотическая система охлаждения, двигатели одинаковых размеров (асинхронные, постоянного тока и т.д.) имеют примерно одинаковые средние нагрузки независимо от типа. Как мы увидим, это ведёт, в свою очередь, к тому, что двигатели одинаковых размеров имеют одинаковые моментные возможности. Этот факт не очень-то оценивается пользователями, но всегда присутствует.
1.5.2 Момент и размеры двигателя
В свете предыдущих обсуждений, мы можем получить общую тангенциальную силу, в первом приближении, в области поверхности ротора шириной w и длиной L. Аксиальный ток, протекающий по участку ротора шириной w, определяется как I = w ![]() , и в среднем весь этот ток взаимодействует с радиальным потоком плотности
, и в среднем весь этот ток взаимодействует с радиальным потоком плотности ![]() , поэтому тангенциальная сила определяется (из формулы 1.2) как
, поэтому тангенциальная сила определяется (из формулы 1.2) как ![]() х w
х w![]() x L. Площадь поверхности определяется как wL, поэтому сила на единицу площади будет
x L. Площадь поверхности определяется как wL, поэтому сила на единицу площади будет ![]() х
х![]() . Мы видим, что произведение двух средних нагрузок выражает среднее тангенциальное усилие по всей поверхности ротора.
. Мы видим, что произведение двух средних нагрузок выражает среднее тангенциальное усилие по всей поверхности ротора.
Чтобы получить общую тангенциальную силу мы должны умножить силу единичной площади на всю площадь поверхности ротора, а чтобы получить общий момент мы перемножим общую силу на радиус ротора. Следовательно, для ротора диаметром D и длиной L, общий момент даётся как

Эта формула исключительно важна. Выражение D2 L пропорционально объему ротора, отсюда мы видим, что для заданных величин средних магнитной и электрической нагрузок, момент для любого двигателя пропорционален объему ротора. Мы свободны в выборе длинного и тонкого ротора или короткого и толстого, но как только мы определились с объемом ротора, мы задали и момент.
Ценно, что мы не фокусировались на типе двигателя, а рассматривали создание момента, исключительно основываясь на базовых принципах. Суть наших выводов отражает тот факт, что все двигатели делаются из железа и меди, а отличаются только способом их расположения. Мы должны признать, что на практике габаритные размеры двигателя более важны, чем размеры только ротора. Однако очевидна вполне определённая связь между размерами двигателя и ротора для любого типа двигателей. Поэтому мы можем сделать дерзкое, но достаточно точное заключение о том, что общий объем двигателя определяет момент, который он может создать. Имеются, конечно, исключения из этого правила, но в целом для выбора двигателя это правило вполне применимо.
Обнаружив зависимость момента двигателя от объема ротора, теперь мы должны обратить внимание на вопрос выходной мощности.
1.5.3 Средняя выходная мощность – важность скорости
Перед тем как вывести выражение мощности, короткое отступление для тех, кто больше знаком с линейным движением чем с круговым.
В системе СИ единицей работы или энергии является Джоуль (J).
Один джоуль это работа выполненная силой в 1 ньютон на расстоянии 1 метр в направлении действия силы. Следовательно, выполненная силой F на расстоянии d работа (W) определяется как

Здесь F в ньютонах и d в метрах, W очевидно в ньютонах на метр (Nm), откуда мы видим, что ньютон на метр то же самое, что и джоуль.
При круговом движении более удобно определять работу в терминах момента и углового расстояния, чем в терминах силы и линейного расстояния, однако эти понятия тесно связаны друг с другом как мы можем увидеть, представив момент как тангенциальную силу F действующую на расстоянии r от центра вращения

Теперь представим, что эта сила продвинулась по окружности на угол θ, окружное расстояние пройденное силой будет r x θ. Работа проделанная силой будет

Мы видим, что в то время как при линейном движении работа есть сила, умноженная на расстояние, при круговом движении работа есть момент, умноженный на угол. Единицей измерения момента есть ньютон на метр, а угол измеряется в радианах (он безразмерен), поэтому, как и ожидалось, единицей измерения работы является Nm, или Джоуль. (Тот факт, что момент и работа (или энергия) измеряются в тех же самых единицах, не кажется автору очевидным!).
Чтобы найти мощность, или оценку работоспособности, мы разделим выполненную работу на затраченное время. При линейном движении, предполагая скорость постоянной, имеем

где v линейная скорость. Эквивалент для кругового движения будет

где ω (постоянная) угловая скорость в радианах в секунду.
Теперь мы можем выразить выходную мощность в терминах размеров ротора и средних нагрузок, используя формулу 1.9, которая даёт

Формула 1.13 подчёркивает важность скорости в определении выходной мощности. Для заданных средних нагрузок, если мы хотим получить требуемую мощность, у нас есть выбор между большим (и поэтому дорогим) низкоскоростным двигателем и маленьким (дешёвым) но высокоскоростным. Последняя опция более предпочтительна для большинства применений, даже если требуется снижение скорости (используя шкивы или редукторы) поскольку маленький мотор дешевле. Общеизвестные примеры включают ручной электрический инструмент, где скорость ротора 12000 об/мин или больше позволяет получить мощность сотни ватт и электрическую тяговитость: где всегда высокая скорость двигателя снижается редуктором для окончательного использования. В этих примерах, где объем и вес, являются определяющими, непосредственный привод вообще не рассматривается.
Важность скорости подчёркивается, когда мы преобразуем формулу 1.13 чтобы получить выражение для средней выходной мощности (мощность на единицу объема ротора), Q

Чтобы получить максимально возможный средний выход для заданных величин средних магнитной и электрической нагрузок, необходимо использовать двигатель при максимально возможной скорости. Одним очевидным недостатком маленьких высокоскоростных двигателей и редукторов является акустический шум (как самого двигателя, так и трансмиссии), который больше чем больших двигателей с непосредственным приводом. В случаях, когда шум должен быть минимизирован (например, для вентилятора на потолке), двигатель с непосредственным приводом предпочтительнее, несмотря на больший размер.
1.6 ПРЕОБРАЗОВАНИЕ ЭНЕРГИИ – ЭЛЕКТРОДВИЖУЩАЯ СИЛА (ЭДС)
Сейчас мы уйдём от рассмотрения того, что определяет в целом возможности двигателя, к другой крайности, исследуя поведение простого линейного двигателя, который, несмотря на простоту, вобрал в себя весь процесс преобразования электромагнитной энергии, имеющий место в электрических двигателях. Мы увидим, как процесс преобразования энергии из электрической в механическую форму элегантно представляется «эквивалентной схемой». Все ключевые аспекты поведения двигателя могут быть рассчитаны с её помощью. Эта цепь будет давать ответы на такие вопросы как «как двигатель автоматически создаёт больше мощности, чем требуется для работы», или «что определяет постоянную скорость и ток». Центральным вопросом является вопрос об электродвижущей силе, которая рассматривается далее.
Мы уже видели, что сила (а, следовательно, и момент) создаются на токопроводящих проводниках, взаимодействующих с магнитным полем. Сила определяется формулой 1.2, которая показывает, что пока плотность потока и ток остаются постоянными, сила также будет постоянной. В частности мы видим, что сила не зависит от того движется проводник или стационарен. С другой стороны, относительный момент является существенным требованием для выработки выходной механической мощности (очевидно из момента). Мы увидели, что выходная мощность даётся формулой P = T ω. Сейчас мы увидим, что присутствие относительного движения между проводниками и полем всегда создаёт электродвижущую силу; мы увидим, что электродвижущая сила играет ключевую роль в определении количества преобразованной энергии.
1.6.1 Элементарный двигатель – стационарные условия, (v=0)
Примитивный линейный двигатель изображен художественно на Фигуре 1.13 и схематично на Фигуре 1.14.
Он состоит из проводника, с активной длиной l который может перемещаться в горизонтальной плоскости перпендикулярной плотности магнитного потока B.
Предполагается, что проводник имеет сопротивление (R), и через него протекает постоянный ток (I), а также, что он движется с постоянной

скоростью (v) в направлении перпендикулярном полю и току (смотри Фигуру 1.14). К проводнику одним концом прикреплена нить, пропущенная через шкив, на втором конце которой подвешен груз: натяжение нити действует как механическая «нагрузка» на стержень проводника. Трение предполагается равным нулю.
Нам нет нужды беспокоиться о многих практических трудностях изготовления такого двигателя, ни о том, как обеспечить электрическое соединение с движущимся проводником. Важным является только то, что несмотря на всю гипотетичность устройства, оно отражает природу реального двигателя и позволяет нам получить ясное понимание его поведения до того как мы возьмёмся за более сложные устройства.
Мы начнём рассмотрение входной электрической мощности при неподвижном проводнике (т.е. v = 0). Для целей нашего рассмотрения можно полагать, что магнитное поле (B) создаётся постоянными магнитами.

После того как поле было создано (имеются ввиду изготовление и размещение магнитов) для его поддержания не требуется никакой энергии, поскольку очевидно, что нейтральный магнит не в состоянии постоянно поставлять энергию. Отсюда следует, что когда мы получим механическую энергию на выходе двигателя, ни какая её часть не будет взята от магнита. Это исключительно важный вывод: поле, не важно, созданное постоянным магнитом или катушками возбуждения, является только катализатором процесса преобразования энергии и не добавляет ничего к выходной механической мощности.
Когда проводник неподвижен сила, возникающая на нём (BIl) не создаёт работы, следовательно, нет выходной механической мощности, а требуется только электрическая мощность чтобы создать движение тока в проводнике. Сопротивление проводника – R, ток через него – I, поэтому напряжение, которое должно быть подведено к концам стержня даётся выражением V1 = I R, а электрическая входная мощность будет V1 I или I2 R . При этих условиях вся электрическая входная мощность пойдёт на нагревание проводника, а баланс мощности может быть выражен равенством:
электрическая входная мощность (V1 I) = величина, выделенного
тепла в проводнике (I2 R). (1.15)
Хотя работа не была произведена, поскольку нет движения, стационарные условия могут поддерживаться только при равенстве сил. Натяжение нити (T) будет равно силе притяжения земли для массы (mg), а она, в свою очередь, должна компенсироваться электромагнитной силой на проводнике (BIl). Следовательно, для стационарных условий ток определяется из выражения

Впервые в этой книге формула показывает связь между механическим и электронным миром, мы видим, что для поддержания стационарных условий ток в проводнике определяется массой механической нагрузки. Мы вернёмся к этой связи позже.
1.6.2 Отношения мощности – при движении проводника с постоянной скоростью
Теперь представим случай, когда проводник движется с постоянной скоростью (v) в направлении действия электромагнитной силы его толкающей. Какой ток должен быть в проводнике, какое напряжение должно прикладываться к его концам?
Мы начнём с уточнения о том, что постоянная скорость проводника означает движение вверх массы (m) с постоянной скоростью, т.е. без ускорения. Следовательно, согласно закону Ньютона на массу не действует несбалансированная сила и натяжение нити (T) определяется весом (mg). Аналогично, проводник не ускоряется и его несбалансированная сила также равна нулю. Нить натягивается тормозящей силой (T), поэтому электромагнитная сила (BIl) должна быть равна T. Учитывая эти условия, выводим

Это точно такое же выражение, что мы получили для стационарных условий, и согласуется с тем фактом, что установившийся ток определяется механической нагрузкой. Когда мы построим эквивалентную схему, мы должны будем учесть тот факт что установившееся состояние электрических переменных (тока) определяется механической нагрузкой.
С поднятием массы при постоянной скорости, выполняется механическая работа, поскольку потенциальная энергия массы увеличивается. Эта работа выполняется движущимся проводником. Выходная механическая мощность равна величине этой работы, т.е. силе (T = BIl) умноженной на скорость (v). Мощность потерянная как тепло в проводнике будет такой же, как и в стационарных условиях, так как тоже сопротивление и тот же ток. Подводимая электрическая мощность должна питать проводник непрерывно, чтобы обеспечить эту тепловую потерю, а также обеспечить выходную механическую мощность. Поскольку мы ещё не знаем какое напряжение должно питать проводник, обозначим его как V2. Уравнение сохранения мощности теперь становится таким
входная электрическая энергия (V2I) = величина выделенного в проводнике тепла + механическая выходная мощность
= I2 R + (BIl)v (1.18)
Мы отмечали, что первое слагаемое в правой части уравнения 1.18 отражает эффект нагревания, который точно такой как в случае со стационарным проводником, в тоже время второе слагаемое отражает дополнительную мощность необходимую для создания механического выхода. Поскольку ток тот же, что и в первом случае, а входная мощность больше, напряжение V2 должно быть больше чем V1. Вычитая уравнение 1.15 из уравнения 1.18, мы получим

Выражение 1.19 определяет дополнительное напряжение, которое необходимо обеспечить от внешнего источника для поддержания постоянного тока в проводнике при его движении. Это увеличение напряжения от внешнего источника отражает тот факт, что как только происходит перемещение проводника в магнитном поле, ЭДС (E) возникает в нём.
Из уравнения 1.19 мы видим, что ЭДС прямо пропорциональна плотности потока, скорости движения проводника относительно магнитного поля и активной длине проводника. Внешний источник должен преодолеть это дополнительное напряжение чтобы обеспечить тот же ток: если питающее напряжение не увеличивается ток уменьшится, как только проводник начнёт движение, вследствие эффекта ЭДС.
Мы установили наличие ЭДС из-за движения проводника, вывели уравнение для неё, основываясь на принципе сохранения энергии, и получили результат

часто представляемый как «обрезание потока» в законе Фарадея, который определяет, что когда проводник движется сквозь магнитное поле, заданная уравнением 1.20 ЭДС, индуцируется в нём. Поскольку движение является основополагающей частью этого механизма, ЭДС называют: электродвижущей силой. Термин «обрезание потока» возникает в связи с происхождением ЭДС, когда движение проводника пересекает силовые линии магнитного потока. Это удобная идеализация для линий потока, но не стоит слишком увлекаться, простыми объяснениями в попытке осмыслить вопросы магнетизма.
Перед тем как перейти к эквивалентной цепи примитивного двигателя есть смысл сделать два общих замечания. Во-первых, всякий раз, когда происходит преобразование электрической энергии в механическую энергию, индуцируемая ЭДС действует противоположно питающему напряжению. Это отражается в термине «ПротивоЭДС» чтобы описать ЭДС в двигателях. Во-вторых, хотя мы рассматривали пример, в котором по проводнику течёт ток, в общем случае это не является необходимым для возникновения ЭДС: всё, что требуется так это движение проводника по отношению к магнитному полю.
1.7 ЭКВИВАЛЕНТНАЯ СХЕМА
Мы можем представить электрические взаимодействия в примитивном двигателе эквивалентной схемой показанной на Фигуре 1.15.
Сопротивление проводника и ЭДС вместе моделируют процессы, происходящие в проводнике (хотя в реальности ЭДС и сопротивление распределены по проводнику, а не собраны в какие-то отдельные центры). Внешний питающий источник, который обеспечивает ток, моделируется напряжением V указанным на левой стороне схемы (используется старый символ батареи, чтобы было различие с индуцированной ЭДС). Отметим, что источник ЭДС включен встречно с питающим напряжением, как обсуждалось ранее, это соответствует «двигательному» варианту возникновения ЭДС.
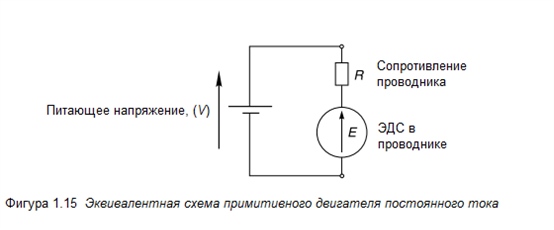
Применяя закон Кирхгофа, получим выражение для напряжения

Умножая формулу 1.21 на ток, получаем уравнение для мощности

(Отметим, что термин «потери в меди» использованный в уравнении 1.22 относится к обозначению тепла выделенного в проводнике под действием тока в обмотках: все такого рода потери в электрических двигателях обозначаются, таким образом, даже если проводники сделаны из алюминия или бронзы!)
Стоит изучить эти уравнения поскольку, как сказано ранее, этот примитивный двигатель вобрал в себя существенные особенности реальных двигателей. Выводы, которые появляются на данный момент, будут полезны позже, когда мы рассмотрим работу реальных двигателей.
Если ЭДС E меньше чем питающее напряжение V, ток будет положительный и электрическая мощность от источника, в конце концов, будет преобразована в работу двигателя. В другом случае, если E больше чем V ток будет течь, наоборот, в источник и мотор будет работать как генератор. Эта прирождённая способность переключаться из двигательного в генераторный режим без всякого вмешательства пользователя является исключительно желательной для электромагнитных преобразователей. Наше примитивное устройство является просто машиной способной работать дома либо как двигатель, либо как генератор.
Следующий важный момент, который нужно учесть это то, что механическая мощность (первое слагаемое в правой части уравнения 1.22) есть простое произведение ЭДС на ток. Этот результат опять же является универсальным и легко запоминаемым. Иногда нам надо будет быть внимательными с ЭДС и током, если это не постоянный ток, но основная идея всё равно остаётся в силе.
И в заключении, очевидно, наше желание для двигателя чтобы как можно больше входной электрической энергии было преобразовано в выходную механическую энергию и как можно меньше в тепло в проводнике. Поскольку выходная мощность есть EI , а потери тепла есть I 2R, мы видим, что в идеале желательно, чтобы EI было как можно больше чем I 2R , или другими словами, E должно быть значительно больше чем IR. Для эквивалентной схемы (Фигура 1.15) это означает, что основная часть питающего напряжения V должна расходоваться на ЭДС (E) и только малая часть на преодоление сопротивления.
1.7.1 Режим двигателя
В режиме двигателя проводник перемещается в том же направлении что и электромагнитная сила (BI l), а скорость такова, что ЭДС (B lv) меньше чем питающее напряжение V. В наших рассуждениях до сих пор мы предполагали, что нагрузка постоянна, поэтому в установившемся режиме ток тот же самый для всех скоростей, напряжение увеличивалось вместе с ростом скорости, чтобы компенсировать ЭДС. Такое допущение помогает понять связь между мощностями в стационарном режиме, однако редко имеет место на практике. Поэтому рассмотрим поведение проводника в ситуации, когда питающее напряжение V постоянно, поскольку это больше соответствует реальности.
Рассматриваемые в следующей части вопросы неизбежно более сложные, чем были до этого, поскольку мы рассматриваем двигатель при изменении скорости и достижении установившегося режима. Как и в любой другой области динамики, рассмотрение переходного процесса в нашем примитивном двигателе приводит к необходимости рассматривать дополнительный параметр, такой как масса проводника (это эквивалент инерции реального двигателя), который отсутствовал при рассмотрении стационарного режима.
1.7.2 Поведение без механической нагрузки
В этой части мы предполагаем, что подвешенный груз был снят, а на проводник действует только его собственная электромагнитная сила. Наш главный интерес в том чтобы узнать – что определяет установившуюся скорость примитивного двигателя, но сначала мы рассмотрим – что происходит при подаче питающего напряжения.
При неподвижном проводнике, когда подаётся питающее напряжение V, ток немедленно увеличится до величины V/R, поскольку нет ЭДС, и только сопротивление проводника ограничивает ток. (Строго говоря, мы должны учитывать индуктивность при возрастании тока, но для простоты сейчас это игнорируется). Сопротивление будет маленьким, поэтому ток большим и, следовательно, большая электродвижущая сила возникнет на проводнике. Проводник начнёт двигаться с ускорением равным силе делённой на его массу. Одновременно с началом движения начнёт расти ЭДС (формула 1.20) пропорционально скорости. Поскольку ЭДС действует против питающего напряжения, ток начнёт уменьшаться (формула 1.21), а за ним сила и ускорение движения также, но рост скорости будет продолжаться, однако не так быстро как в начале. Скорость будет увеличиваться, пока существует ускоряющая сила, т.е. пока есть ток в проводнике. Мы можем видеть из формулы 1.21, что ток упадёт до нуля, когда скорость достигнет величины, при которой ЭДС станет равной питающему напряжению. Поэтому скорость и ток изменяются, как показано на Фигуре 1.16: обе кривые имеют экспоненциальную форму, которая характерна для систем описываемых дифференциальными уравнениями первого порядка. Тот факт, что установившийся ток равен нулю согласуется с предыдущим выводом о том, что установившийся ток определяется механической нагрузкой (в данном случае это ноль).

В такой идеализированной ситуации (когда нет нагрузки и сил трения) проводник будет двигаться с постоянной скоростью, так как нет силы действующей на него, и значит ускорения. Конечно, не производится механическая мощность, поскольку нет никакой противодействующей силы приложенной к проводнику, и не потребляется входная мощность, поскольку ток равен нулю. Тем не менее, эта гипотетическая ситуация очень близка к реальному режиму «холостого хода», отличие только в том, что реальный двигатель имеет трение (и следовательно это создаст небольшой ток), а мы трение исключили для простоты рассуждений.
Хотя условия отсутствия трения и нагрузки на проводник предполагают отсутствие потребляемой мощности, во время переходного процесса питающее напряжение остаётся постоянным, а ток уменьшается, поэтому потребляемая входная мощность была большой в первый момент и уменьшалась с ростом скорости. В течение времени этого разгона энергия постоянно потреблялась от источника: часть её была потеряна в виде тепла в проводнике, но основная часть преобразована и запасена в виде кинетической энергии проводника, и как мы увидим позже, может быть возвращена.
Как видно элегантный механизм саморегулирования работает здесь. Сначала, когда проводник неподвижен, на него воздействует большая сила, но она уменьшается с ростом до заданной скорости, при которой ЭДС равна питающему напряжению. Из формулы для ЭДС (формула 1.19) мы можем получить выражение для скорости без нагрузки (v0) приравнивая питающее напряжение и ЭДС

Уравнение 1.23 показывает, что установившаяся скорость без нагрузки прямо пропорциональна питающему напряжению, это подсказывает возможность управлять скоростью с помощью питающего напряжения. Позже мы увидим, что одной из основных причин, почему двигатели постоянного тока доминировали в области управления скоростью так долго, является возможность контролировать скорость простым управлением питающим напряжением.
Это удивительно, но уравнение 1.23 обнаруживает обратно пропорциональную зависимость скорости от плотности магнитного потока, это означает, что чем слабее поле, тем выше установившаяся скорость. Этот вывод может вызвать удивление по понятным причинам. Действительно, поскольку сила возникает под действием поля логично предположить, что проводник не может двигаться быстрее, если поле слабее. Это предположение ошибочно, хотя и понятно. Поток в основании уравнения для того чтобы сбалансировать силу со скоростью. При подаче питающего напряжения, сила на проводнике, определённо будет меньше, если поле слабее, и ускорение также будет меньше. Но в любом случае ускоренное движение будет продолжаться, пока ток не упадёт до нуля, а это произойдёт только, когда индуцированная ЭДС возрастет и станет равной питающему напряжению. При ослабленном поле, большая скорость нужна, чтобы получить такую же ЭДС. Таким образом, уменьшение потока приводит к равенству ЭДС и питающего напряжения при большей скорости. Этот эффект показан на Фигуре 1.17,

где видно как скорость будет возрастать до заданного питающего напряжения для «полного» и «половинного» потоков соответственно. Обратите внимание, что первоначальное ускорение (т.е. наклон кривой скорость-время) при половине потока будет вдвое меньше чем при полном потоке, но окончательная установившаяся скорость вдвое больше. В реальных двигателях постоянного тока метод уменьшения плотности потока для увеличения скорости известен под названием «ослабление поля».
1.7.3 Поведение с механической нагрузкой
Предположим, что мы присоединили нить с весом к примитивному линейному двигателю, работавшему без механической нагрузки, появляется сила (T = mg) направленная против движения проводника. В этот момент только сила T воздействует на проводник, поскольку ток равен нулю. По этой причине проводник начнёт замедляться в своём движении. Но как только скорость начнёт падать, ЭДС становиться меньше V, и ток начнёт течь через проводник, создавая электродвижущую силу. Чем больше падение скорости, тем больше ток, а значит и сила, возникающая на проводнике. Когда эта сила на проводнике станет равной нагрузке (T), замедление движения проводника прекратится и будет достигнуто новое равновесие. Скорость будет меньше, чем была без нагрузки, а проводник теперь будет вырабатывать постоянную выходную механическую мощность, т.е. работать как двигатель.
Поскольку электромагнитная сила на проводнике прямо пропорциональна току, то отсюда следует, что установившееся значение тока прямо пропорционально действующей нагрузке, как мы видели ранее. Если бы мы захотели смоделировать математически переходный процесс, то получили бы туже экспоненциальную кривую что и при разгоне ранее. Снова очевидно свойство саморегулирования, когда возникает нагрузка, скорость падает ровно на столько, чтобы возник достаточный ток для возникновения силы балансирующей эту нагрузку. Вряд ли мы хотели бы что-нибудь лучше, поскольку проводник всё делает без нашего участия. Читатели, которые знакомы с замкнутыми системами управления, вероятно, заметят, что причиной таких великолепных свойств является наличие отрицательной обратной связи в примитивном двигателе посредством ЭДС. Этот вопрос рассматривается более обстоятельно в Приложении.
Возвращаясь к уравнению 1.21, отметим, что ток напрямую зависит от разницы между V и E, но обратно пропорционален сопротивлению. Далее, для заданного сопротивления, чем больше нагрузка (а значит и установившийся ток), тем больше требуемая разница между V и E, следовательно, меньше установившаяся скорость, как показано на Фигуре 1.18.
Мы также можем видеть из уравнения 1.21, что чем выше сопротивление проводника, тем больше падение скорости при возникновении нагрузки. И наоборот, чем меньше сопротивление, тем больше проводник способен поддерживать скорость холостого хода при наличии нагрузки. Это тоже иллюстрируется на Фигуре 1.18. Можно сделать вывод о существовании только одного пути для получения постоянной скорости этого типа двигателя, сопротивление проводника должно быть равно нулю, это, конечно же, не возможно.

Тем не менее, реальные двигатели постоянного тока обычно имеют маленькое сопротивление, и их скорость не сильно падает под нагрузкой – для большинства применений характеристики хорошие.
Мы дополним наше изучение характеристик под нагрузкой, задав вопрос, а как плотность потока влияет на них? Вспоминая, что электромагнитная сила пропорциональна плотности потока и току, можно сделать вывод - чтобы получить заданную силу, при слабом потоке, нужен больший ток, чем при сильном потоке. Следовательно, учитывая, что всегда существует предел максимального тока, который может безопасно протекать через проводник, максимальная сила зависит от плотности потока, причём, чем больше плотность потока, тем больше максимальная сила. Это подчёркивает важность работы при максимально возможной плотности потока.
Можно увидеть и другой недостаток в работе при маленькой плотности потока, отмечая, что для достижения заданной силы падение скорости будет не пропорционально большим при маленькой плотности потока. Это легче понять, если представить, что будто мы хотим получить какую-то силу сначала при полном потоке, а потом при половине потока. При полном потоке будет некоторое падение скорости и как следствие также ЭДС с допустимым возрастанием тока, до требуемого. Но при половине потока, вдвое больший ток нужен, чтобы получить туже силу. А значит, ЭДС должна упасть в два раза сильнее, чем при полном потоке. Как результат, поскольку плотность потока только половина, падение скорости должно быть в четыре раза больше в сравнении с полным потоком. «Двигатели» с половинным потоком, поэтому имеют нагрузочные характеристики с градиентом в четыре раза более падающим, чем для полного потока. Это показано на Фигуре 1.19; питающие напряжения были выровнены, чтобы скорость холостого хода была одинакова в обоих случаях. Двигатель с половиной потока определённо хуже в смысле его способности удерживать скорость при нагрузке.

Можно подумать, чем выше скорость, которую мы можем получить, уменьшая поток, тем лучше энергетическая характеристика, но это не так. Деля поток пополам, например, скорость холостого хода удваивается для заданного напряжения, но при возрастании нагрузки до номинального тока сила возрастает только на половину, поэтому мощность остаётся той же. Скорость торгуется с силой, но не предлагается получить что-нибудь за ничего.
1.7.4 Относительные значения V и E, и эффективность
Мы всегда хотим двигатели с высокой эффективностью. Из уравнения 1.20 мы видим, чтобы достичь высокой эффективности, потери в меди (I 2R) должны быть маленькими в сравнении с механической мощностью (EI), что означает малое падение напряжения (I R) на сопротивлении в сравнении с ЭДС (E) или питающим напряжением (V). Другими словами мы хотим, чтобы основная часть питающего напряжения предназначалась для «полезной» ЭДС, а не для бесполезного падения напряжения на проводе. Поскольку ЭДС пропорциональна скорости, а падение напряжения на проводнике зависит от его сопротивления, то для хорошего преобразователь энергии необходимо иметь как можно меньшее сопротивление и как можно большую скорость.
Чтобы лучше почувствовать сказанное, предлагается несколько примеров, мы рассмотрим проводник с сопротивлением 0.5 Ом проводящий ток 4 А и двигающийся с такой скоростью, что ЭДС равно 8 В.Из уравнения 1.19 питающее напряжение будет

Следовательно, электрическая входная мощность (VI) ,будет 40 ватт, механическая выходная мощность (EI) будет 32 ватта, а потери в меди (I 2R) будут 8 ватт, давая эффективность 80%.
Если питающее напряжение было увеличено (например, V = 20 вольт), а сила сопротивления предполагается той же (такой что установившийся ток по-прежнему 4 А), ЭДС из уравнения 1.19 будет

это показывает, что скорость возросла более чем в два раза, как и ожидалось. Электрическая входная мощность теперь 80 ватт, механическая выходная мощность 72 ватта, потери в меди по-прежнему 8 ватт. Эффективность возросла до 90%, подчёркивая тот факт, что процесс преобразования энергии идёт лучше при более высоких скоростях.
Идеальная ситуация когда выражение IR в уравнении 1.19 пренебрежимо мало, настолько что ЭДС равно питающему напряжению. Мы бы имели идеальную машину с эффективностью 100% и установившейся скоростью прямо пропорциональной питающему напряжению и независимой от нагрузки.
На практике степень приближения к идеалу, упомянутому выше, зависит от размеров машины. Миниатюрные двигатели, такие как в наручных часах ужасны, основная часть питающего напряжения идёт на покрытие сопротивления в проводниках, а ЭДС очень маленькая: такие двигатели лучше производят тепло, чем выходную механическую мощность! Маленькие двигатели, такие как используются в ручном электроинструменте, работают лучше с ЭДС около 70-80% питающего напряжения. Промышленные двигатели значительно лучше: наиболее крупные (много сотен киловатт) расходуют только один или два процента питающего напряжения на преодоление сопротивления, и поэтому имеют очень высокую эффективность.
1.7.5 Анализ примитивного двигателя – выводы
Почти для всех двигателей в оставшейся части этой книги мы найдём явные параллели со свойствами рассмотренного примитивного двигателя, поэтому есть смысл повторить основные моменты.
Во-первых, мы будем делать частые ссылки на формулу силы (F), на проводнике в магнитном поле

и на формулу ЭДС (E)

где B плотность магнитного потока, I - ток, l – длина проводника, а v – скорость перпендикулярная полю. Эти уравнения формируют теоретическую основу, на которой располагается наше понимание двигателей.
Во-вторых, мы увидели, что скорость, с которой примитивный двигатель работал на холостом ходу, определяется питающим напряжением, тогда как ток, который двигатель потребляет, определяется механической нагрузкой. Точно такие же результаты имеют силу при рассмотрении реальных двигателей постоянного тока, и очень похожие при рассмотрении асинхронного двигателя.
1.8 ОБЩИЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ДВИГАТЕЛЕЙ
Все электрические двигатели подчиняются законам электромагнетизма и в основном одним и тем же ограничениям наложенным материалами (медь и железо), из которых они сделаны. Поэтому мы не должны удивляться, когда обнаружим, что фундаментальный предел для всех двигателей – независимо от типа – в основном общий.
Эти похожие характеристики, большинство из которых было затронуто в этой главе, не являются чем-то особенным. В книгах подчёркиваются различия между разными типами двигателей, а производители обычно заинтересованы в продвижении особенностей конкретного двигателя в условиях усиливающейся конкуренции. Такое подчёркивание частных случаев затеняет наличие общности, оставляя пользователю мало возможностей приобрести знания для обоснованных суждений.
Поэтому наиболее полезные знания даются далее с кратким пояснением для каждого случая. Опыт показывает, что пользователи, крепко усвоившие эти базовые идеи, будут способны понимать, почему один двигатель, кажется лучше, чем другой, будут чувствовать себя более уверенными, когда столкнутся с трудной задачей взвесить все за и против конкурирующих предложений.
1.8.1 Рабочая температура и охлаждение
Устройство охлаждения является главным и наиболее важным фактором определяющим выход любого двигателя.
 Любой двигатель даст больше выходной мощности, если его электрическая сеть работает более напряжённо (т.е. если ток может быть увеличен). Обычно, ограничивающим фактором является допустимый рост температуры обмоток, который зависит от класса изоляции.
Любой двигатель даст больше выходной мощности, если его электрическая сеть работает более напряжённо (т.е. если ток может быть увеличен). Обычно, ограничивающим фактором является допустимый рост температуры обмоток, который зависит от класса изоляции.
Для класса F (наиболее широко распространённого) допустимый рост температуры 100K, тогда как для класса H 125K. Таким образом, если охлаждение одинаковое, больше выхода можно получить, просто используя изоляцию более высокого класса. Наоборот, при заданной изоляции выход можно увеличить, если улучшить охлаждение. Например, двигатель со сквозной вентиляцией может дать примерно вдвое больше выходной мощности, чем идентичный, но полностью закрытый.
1.8.2 Момент на единицу объёма
Для двигателей с одинаковыми охлаждающими системами, номинальный момент примерно пропорционален объёму ротора, который в свою очередь примерно пропорционален объёму двигателя.
Это следует из факта, что для данной охлаждающей системы, заданные и магнитные нагрузки двигателей разных типов будут, примерно одинаковы. Момент на единицу длины, поэтому зависит прежде и больше всего от квадрата диаметра, отсюда от двигателей примерно одинакового диаметра и длины можно ожидать примерно одинаковые моменты.
1.8.3 Мощность на единицу объёма – важность скорости
Выходная мощность прямо пропорциональна скорости.
Низко скоростные двигатели не привлекательны потому, что они большие, а значит дорогие. Обычно гораздо лучше использовать высокоскоростные двигатели с механическим уменьшением скорости. Например, двигатель с непосредственным приводом для ручного шуруповёрта был бы неразумным предложением.
1.8.4 Эффекты размера – заданные момент и эффективность
Большие моторы имеют больший заданный момент (момент на единицу объёма) и более эффективны, чем маленькие.
В больших моторах заданная электрическая нагрузка обычно значительно больше, чем у маленьких, а заданная магнитная нагрузка немного больше. Эти два фактора обеспечивают более высокий заданный момент.
Очень маленькие двигатели являются по существу очень не эффективными (например, 1% в наручных часах), тогда как двигатели свыше 100 кВт имеют эффективность более 95%. Причины такого разброса не просты, но основаны на том факте, что падение напряжения на сопротивлении можно сделать относительно маленьким в больших электромагнитных устройствах, в то время как в маленьких это сопротивление становится доминирующим фактором.
1.8.5 Эффективность и скорость
Эффективность двигателей повышается с увеличением скорости.
Для заданного момента, выходная мощность растёт прямо пропорционально скорости, хотя электрические потери, вообще-то, остаются постоянны. В этих условиях, эффективность растёт со скоростью.
1.8.6 Номинальное напряжение
Двигатель можно приспособить для любого напряжения.
В определённых пределах двигатель всегда можно перемотать для различного напряжения без воздействия на его характеристики. Двигатель 200 В, 10 А может быть перемотан для 100 В, 20А просто используя половину витков провода с вдвое большим поперечным сечением. Общее количество используемого материала, а значит и характеристики, будут те же.
1.8.7 Кратковременная перегрузка
Большинство двигателей могут быть кратковременно перегружены без повреждений.
Длительная электрическая нагрузка (например, ток) не может быть превышена без повреждений изоляции, однако, если двигатель работал некоторое время при пониженном токе, допускается для тока (и момента) перегрузка на короткий промежуток времени. Принципиальными факторами, влияющими на величину и продолжительность допустимой перегрузки, являются температурная постоянная (которая определяется степенью роста температуры) и предыдущий режим работы двигателя. Диапазон температурных постоянных от нескольких секунд, для маленьких двигателей, до нескольких минут и даже часов для больших двигателей. Режимы работы очевидно очень разные, поэтому предпочитают не ограничиваться рекомендациями, а обеспечить двигатель устройством защиты от перегрева (например, термистором) который включает тревогу и (или) выключает напряжение, если безопасная температура превышена.
| Свет: основные понятия и их практическое применение |
| Что такое БКТП? |
| Сварка. Основные виды сварки. Сварка различных металлов с сплавов. |

