Зонная теория электропроводности твердых материалов

Содержание страницы

1. Атомная структура вещества: Базовые определения
2. Квантово-механические основы
3. Формирование энергетических зон
4. Классификация материалов по зонной теории
5. Природа электрического сопротивления в металлах
6. Практические выводы
7. Интересные факты о природе проводимости
8. Часто задаваемые вопросы (FAQ)
Заключение

Что заставляет медь проводить ток, стекло — изолировать его, а кремний — переключаться между этими состояниями? Ответ лежит глубоко в структуре материи, на уровне, где классическая ньютоновская физика перестает работать, уступая место законам квантовой механики. Данный материал представляет собой всеобъемлющее руководство по зонной теории твердого тела — фундаментальной концепции, лежащей в основе всей современной электроники, энергетики и материаловедения.

Историческая справка: Попытки объяснить проводимость предпринимались еще в 1900 году П. Друде, создавшим классическую электронную теорию. Однако она не могла объяснить многие явления, например, зависимость сопротивления от температуры в полупроводниках или теплоемкость металлов. Революция произошла с появлением квантовой механики в 1920-х годах. Фундамент зонной теории был заложен Феликсом Блохом в 1928 году (теорема Блоха) и развит Аланом Вильсоном в 1931 году, что позволило четко разделить металлы, полупроводники и диэлектрики.

Замечание: Зонная теория объясняет, почему греется проводка, как работают транзисторы в процессоре вашего компьютера и почему сварной шов имеет иное сопротивление, чем основной металл.

1. Атомная структура вещества: Базовые определения

Для глубокого понимания процессов переноса заряда необходимо спуститься на атомарный уровень. Природа электропроводности твердых электротехнических материалов неразрывно связана с их внутренней архитектурой.

1.1. Атом как строительный блок

Атом — это наименьшая частица химического элемента, являющаяся носителем его свойств. Несмотря на свое название (от греч. atomos — неделимый), атом имеет сложную внутреннюю структуру.

Рис. 1. Изображение атомов, полученное с помощью атомно-силового микроскопа. Визуализация показывает периодическую структуру поверхности кристалла, где светлые пятна соответствуют положению атомов.

Современная физика описывает атом как систему, состоящую из:

Ядра: Положительно заряженный центр, концентрирующий в себе более 99.9% массы атома. Состоит из протонов и нейтронов.
Электронного облака: Отрицательно заряженной оболочки, окружающей ядро. Размеры электронного облака определяют эффективный диаметр атома, который для большинства элементов составляет порядка $ 0,1 $ нм ($ 10^{-10} $ м или 1 Ангстрем).

В невозбужденном (основном) состоянии атом электрически нейтрален: суммарный заряд отрицательных электронов компенсирует заряд положительного ядра. Нарушение этого баланса приводит к ионизации.

Аналогия: Если представить ядро атома размером с вишню, помещенную в центр футбольного стадиона, то электроны будут летать по самым верхним трибунам этого стадиона. Все остальное пространство — это физический вакуум, пронизанный полями. Именно в этом «пустом» пространстве и происходят взаимодействия, определяющие ток.

1.2. Ионы и их роль

В процессе химических реакций или под воздействием внешних полей атомы могут менять свой зарядовый статус:

Положительный ион (катион): Атом, утративший один или несколько электронов. В металлах именно положительные ионы образуют узлы кристаллической решетки.
Отрицательный ион (анион): Атом, захвативший лишние электроны (характерно для неметаллов).

2. Квантово-механические основы

Классическая механика не способна описать поведение микрочастиц. На этом уровне вступают в силу законы квантовой физики, постулирующие дуализм материи.

2.1. Корпускулярно-волновой дуализм

Согласно квантовой механике, элементарные частицы (электроны) проявляют свойства и частицы (корпускулы), и волны. Это означает, что электрон при движении ведет себя подобно световой волне, испытывая дифракцию и интерференцию.

Движение частицы сопровождается так называемыми волнами де Бройля. Длина такой волны $ \lambda $ связана с импульсом частицы $ p $ соотношением:
$$ \lambda = \frac{h}{p} = \frac{h}{mv} $$
где $ h $ — постоянная Планка ($ 6.626 \times 10^{-34} $ Дж·с).

2.2. Принцип неопределенности Гейзенберга

Следствием волновой природы является невозможность точного одновременного определения координат и импульса частицы. Это фундаментальное ограничение сформулировано в принципе неопределенности Гейзенберга:

\Delta x \cdot \Delta p_x \geq \frac{h}{4\pi}

Это означает, что нельзя точно сказать, где находится электрон и куда он летит. Можно лишь говорить о вероятности его нахождения в той или иной области пространства.

2.3. Уравнение Шредингера

Для описания состояния квантовых частиц используется основное уравнение нерелятивистской квантовой механики — уравнение Шредингера. В общем виде для стационарных состояний (с учетом обозначений из вашего курса) оно выглядит так:

\frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} + \frac{\partial^2 \psi}{\partial z^2} + \frac{8\pi^2 m}{h^2}(W — W_p)\psi = 0

Расшифровка параметров уравнения (2.1):

$ h $ — постоянная Планка;
$ m $ — масса частицы (электрона);
$ \psi $ (пси) — волновая функция. Сама по себе она не имеет физического смысла, но квадрат ее модуля $ |\psi|^2 $ определяет плотность вероятности нахождения электрона в данной точке пространства;
$ x, y, z $ — пространственные координаты;
$ W $ — полная энергия частицы;
$ W_p $ — потенциальная энергия частицы (зависит от координат);
Разность $ W — W_p = W_k $ представляет собой кинетическую энергию.

Уравнение Шредингера — это дифференциальное уравнение в частных производных второго порядка. В общем виде оно не имеет аналитического решения. Точные решения существуют только для простейших моделей: свободная частица, частица в прямоугольной потенциальной яме, гармонический осциллятор и атом водорода. Для сложных систем используются приближенные методы.

3. Формирование энергетических зон

Как мы переходим от отдельного атома к твердому телу? Это ключевой момент теории.

3.1. От уровней к зонам

В изолированном атоме электроны находятся на строго определенных дискретных энергетических уровнях. Но когда атомы сближаются, образуя кристаллическую решетку твердого тела, их электрические поля начинают взаимодействовать.

Согласно принципу запрета Паули, в одной квантовой системе (кристалле) не может быть двух электронов с абсолютно одинаковым набором квантовых чисел. Поэтому, когда $ N $ атомов объединяются в кристалл, каждый атомный уровень расщепляется на $ N $ подуровней, расположенных очень близко друг к другу.

Совокупность этих близко расположенных подуровней образует энергетическую зону.

Аналогия: Представьте многоквартирный дом (кристалл). В каждом отдельном доме (атоме) есть 3-й этаж (энергетический уровень). Если построить огромный комплекс из миллиардов домов, то «3-й этаж» превратится в единый высотный пояс — зону.

3.2. Зоны разрешенной и запрещенной энергии

Решение уравнения Шредингера для электрона, движущегося в периодическом поле кристаллической решетки (потенциал Кронига-Пенни), показывает наличие разрывов в спектре возможных энергий.

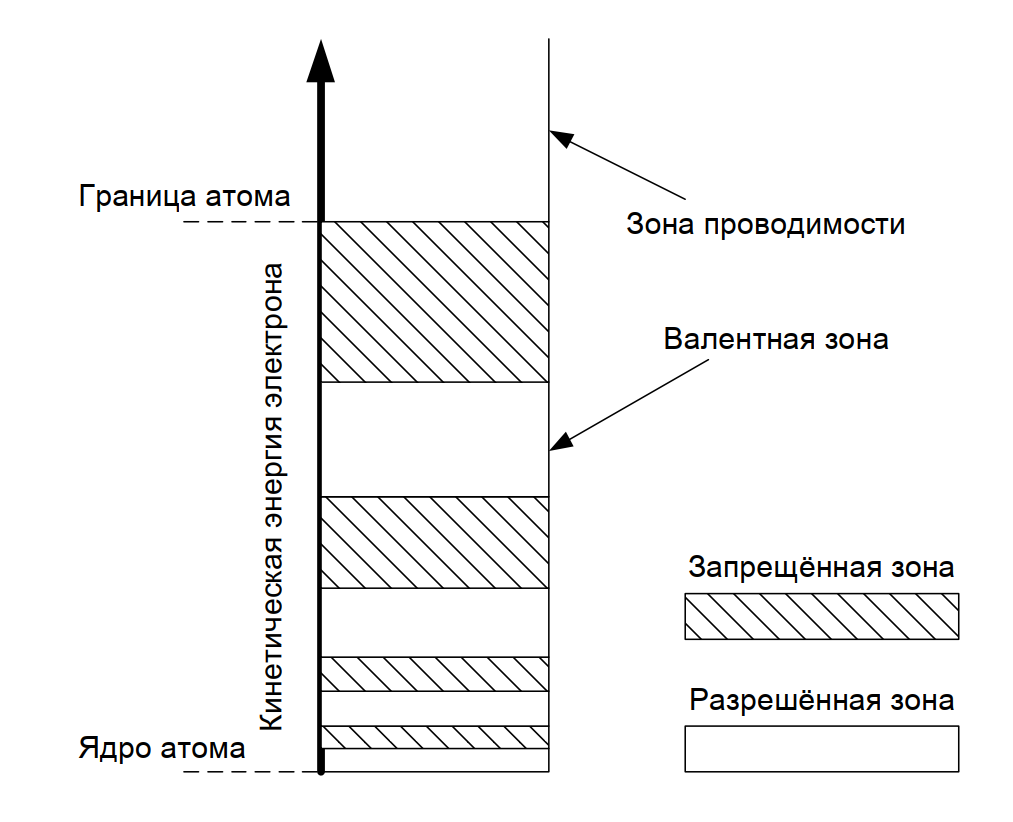
Рис. 2. Энергетическая диаграмма для кинетической энергии электрона. Показана зависимость энергии от расстояния при периодическом потенциале атомов решетки.

Описание диаграммы (Рис. 2):
На рисунке представлена зависимость энергии электрона от его положения в кристалле.

В нижней части расположены Ядра атомов, создающие потенциальные ямы.
Огибающая кривая показывает ход потенциальной энергии.
Выделены диапазоны энергий: Разрешённая зона (где электрон может находиться) и Запрещённая зона (значения энергии, которые электрон иметь не может).
Нижняя заполненная зона обозначена как Валентная зона.
Верхняя зона, куда могут переходить электроны, — Зона проводимости.
Вертикальная ось отражает Кинетическую энергию электрона.

3.3. Валентная зона и зона проводимости

Валентная зона (ВЗ): Самая верхняя из зон, полностью или частично заполненная электронами при абсолютном нуле температуры (0 К). Электроны здесь участвуют в химических связях (ковалентных, металлических), они «привязаны» к атомам и не участвуют в направленном движении заряда (токе) без дополнительной энергии.
Запрещенная зона (ЗЗ): Энергетический промежуток между потолком валентной зоны и дном зоны проводимости. В идеальном кристалле электроны не могут иметь энергию, соответствующую этому диапазону. Ширина запрещенной зоны обозначается $ \Delta W $ или $ E_g $ и измеряется в электрон-вольтах (эВ).
Зона проводимости (ЗП): Расположена выше запрещенной зоны. Электроны, попавшие сюда, освобождаются от связи с конкретным атомом и могут свободно перемещаться по всему кристаллу под действием внешнего электрического поля, создавая ток проводимости.

4. Классификация материалов по зонной теории

Именно ширина запрещенной зоны ($ \Delta W $) является главным критерием, определяющим, будет ли материал проводить ток, будет ли он изолятором или полупроводником.

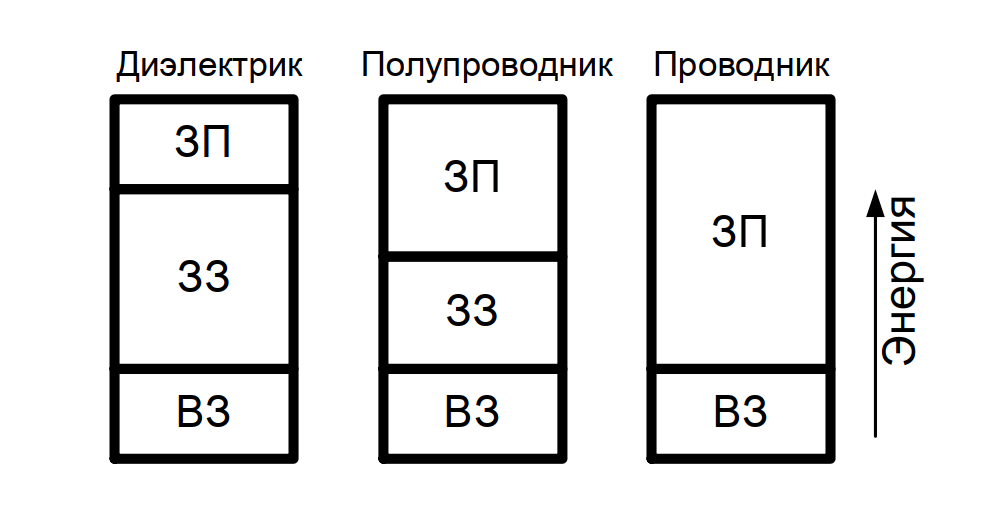
Рис. 3. Энергетические диаграммы различных классов материалов. Обозначения: ЗП – зона проводимости; ЗЗ – запрещенная зона; ВЗ – валентная зона.

4.1. Диэлектрики (Изоляторы)

У диэлектриков (рис. 3, слева) запрещенная зона очень широкая ($ \Delta W > 3…5 $ эВ).

Механизм: Валентная зона полностью заполнена, а зона проводимости пуста. Чтобы перебросить электрон через такую широкую «пропасть», требуется огромная энергия (высокая температура или сильное электрическое поле).
Результат: В обычных условиях свободных носителей заряда нет, ток не течет.
Примеры: Кварц ($ SiO_2 $, ~9 эВ), Алмаз (~5.5 эВ), Полимеры.

4.2. Полупроводники

У полупроводников (рис. 3, центр) ширина запрещенной зоны сравнительно невелика ($ 0.1 < \Delta W < 3 $ эВ).

Механизм: При 0 К полупроводник ведет себя как диэлектрик. Однако при комнатной температуре тепловой энергии ($ kT $) достаточно, чтобы часть электронов преодолела запрещенную зону и перешла в зону проводимости.
Особенность: При уходе электрона в валентной зоне образуется вакантное место — «дырка», которая также участвует в проводимости.
Примеры: Германий ($ Ge $, 0.66 эВ), Кремний ($ Si $, 1.12 эВ), Арсенид галлия ($ GaAs $, 1.42 эВ).

4.3. Проводники (Металлы)

У проводников (рис. 3, справа) запрещенная зона отсутствует ($ \Delta W \approx 0 $).

Вариант А: Валентная зона заполнена не полностью.
Вариант Б: Зона проводимости перекрывается с валентной зоной (гибридизация зон).
Механизм: Электронам не нужно преодолевать энергетический барьер, чтобы стать свободными. Даже при очень низких температурах в металле огромное количество свободных носителей заряда.

Сравнительная таблица материалов

Параметр	Диэлектрики	Полупроводники	Проводники
Ширина ЗЗ ($ \Delta W $)	Большая (> 3-5 эВ)	Средняя (0.1 — 3 эВ)	Отсутствует (0 эВ) или перекрытие
Наличие свободных зарядов (при 20°C)	Ничтожно мало	Умеренное количество	Огромная концентрация (~ $ 10^{22} $ см$^{-3}$)
Зависимость сопротивления от температуры	Падает при сильном нагреве	Резко падает (экспоненциально)	Растет линейно
Основное применение	Изоляция, конденсаторы	Транзисторы, диоды, процессоры	Провода, контакты, шины

5. Природа электрического сопротивления в металлах

Если в металлах так много свободных электронов, почему они вообще обладают сопротивлением? Идеальная кристаллическая решетка не должна оказывать сопротивления движению электронной волны. Сопротивление возникает только из-за нарушений периодичности структуры решетки.

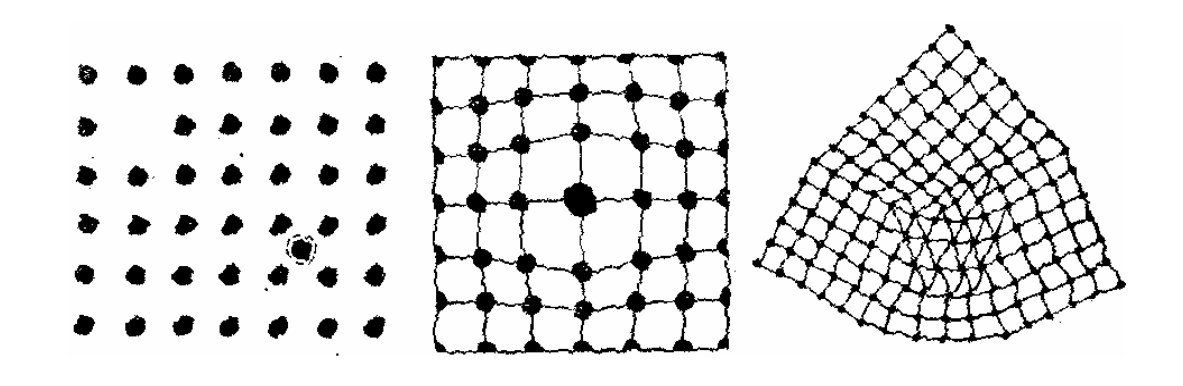
Рис. 4. Дефекты кристаллической решетки, препятствующие движению электронов. Показаны точечные вакансии и внедренные атомы, искажающие поле.

Эти нарушения называются дефектами. Электронная волна де Бройля рассеивается на дефектах, теряя импульс и энергию. Этот процесс рассеяния макроскопически воспринимается как электрическое сопротивление.

Полное удельное сопротивление металла описывается правилом Матиссена:
$$ \rho_{total} = \rho_{therm} + \rho_{res} $$
где $ \rho_{therm} $ — сопротивление, вызванное тепловыми колебаниями (динамические дефекты), а $ \rho_{res} $ — остаточное сопротивление (статические дефекты).

5.1. Статические дефекты (Структурные)

Это постоянные нарушения структуры, не зависящие от температуры (рис. 4):

Примеси и легирование: Чужеродные атомы искажают электрическое поле решетки. Атом примеси может быть больше или меньше атомов основного металла, создавая механические напряжения.
Именно поэтому чистая медь проводит ток лучше, чем латунь (сплав меди с цинком). В сплавах с соотношением компонентов 50:50 хаос в структуре максимален, и сопротивление достигает пика. Это свойство используется для создания высокоомных сплавов (манганин, константан).
Вакансии и междоузлия: Отсутствие атома в узле или наличие лишнего атома в междоузлии.
Дислокации и границы зерен: Линейные и поверхностные дефекты. Поликристаллические материалы (состоящие из множества мелких кристаллитов) проводят хуже монокристаллов из-за рассеяния на границах зерен.
Механические деформации: Наклеп, удары, изгибы создают новые дислокации. В месте удара или перегиба провода кристаллическая решетка искажается, локальное сопротивление растет, что может привести к перегреву в этой точке.

5.2. Динамические дефекты (Тепловые)

Даже в идеально чистом металле атомы не стоят на месте. Они колеблются около положений равновесия. Кванты этих тепловых колебаний называются фононами.

Чем выше температура, тем больше амплитуда колебаний ионов в узлах решетки.
Колеблющиеся ионы чаще «сталкиваются» с электронами (рассеивают электронные волны).
Следствие: С ростом температуры электрическое сопротивление металлов растет. Это фундаментальное свойство учитывается при расчете нагрузочной способности кабелей и при конструировании термометров сопротивления.

Внимание! Радиационное облучение создает как статические дефекты (выбивает атомы из узлов), так и ионизацию. В долгосрочной перспективе это приводит к деградации проводимости материалов, работающих в зоне реакторов или в космосе.

6. Практические выводы

Понимание зонной теории и физики дефектов позволяет сформулировать четкие правила для работы с электротехническими материалами:

Чистота — залог проводимости. Для проводников (кабели, обмотки) следует использовать металлы максимальной чистоты (электротехническая медь M1, M0). Любая примесь ухудшает проводимость.
Сплавы для резисторов. Если нужно высокое сопротивление (нагреватели, реостаты), используйте сплавы с неупорядоченной структурой (нихром, фехраль).
Механическая осторожность. Избегайте лишних изгибов, ударов и перетяжки болтовых соединений. Деформация металла создает области повышенного сопротивления, которые станут очагами нагрева («горячими точками»).
Температурный фактор. При проектировании линий электропередач учитывайте, что в жаркую погоду сопротивление проводов выше, а пропускная способность ниже, чем зимой.
Технология соединений. Сварка меняет структуру металла в зоне шва (рекристаллизация), что может изменить локальное сопротивление. Качественный обжим или пайка минимизируют переходное сопротивление.

7. Интересные факты о природе проводимости

Мир квантовой физики и материаловедения полон явлений, которые кажутся парадоксальными с точки зрения обыденной логики.

Скорость улитки. Хотя электрическое поле распространяется по проводам почти со скоростью света (около 300 000 км/с), сами электроны движутся невероятно медленно. Их «дрейфовая скорость» в медном проводе при обычном токе составляет доли миллиметра в секунду. Лампочка загорается мгновенно не потому, что электрон добежал от выключателя, а потому что «сдвинулась» вся электронная цепь целиком.
Алмазный парадокс. Алмаз является одним из лучших диэлектриков (идеальный изолятор), но при этом он обладает феноменальной теплопроводностью, превышающей теплопроводность меди. Это редкий случай, когда тепло переносится не электронами, а исключительно колебаниями кристаллической решетки (фононами).
Туннельный эффект. В современной Flash-памяти (флешки, SSD) запись информации происходит благодаря квантовому туннелированию. Электроны проходят сквозь слой диэлектрика, который по законам классической физики является для них непреодолимой стеной. Они буквально «телепортируются» сквозь барьер.
Нулевое сопротивление. При температурах, близких к абсолютному нулю, некоторые материалы (сверхпроводники) полностью теряют электрическое сопротивление. Если запустить ток в кольце из такого материала, он будет циркулировать вечно без источника питания.
Золотой миф. Золото проводит ток хуже, чем медь или серебро (удельное сопротивление золота — 0,022, меди — 0,017 мкОм·м). Золотые контакты в электронике используют не из-за проводимости, а исключительно из-за химической инертности — золото не окисляется, обеспечивая надежный контакт годами.
Стекло-проводник. Обычное стекло — отличный диэлектрик при комнатной температуре. Но если его расплавить, кристаллическая решетка разрушается, и ионы натрия и кальция получают подвижность. Раскаленное жидкое стекло становится проводником электрического тока.
Человек-электролит. Электропроводность человеческого тела имеет ионную природу (как в соленой воде), а не электронную (как в металле). Именно поэтому мы обладаем сопротивлением, которое сильно зависит от влажности кожи и даже настроения (психогальванический рефлекс, используемый в детекторах лжи).

8. Часто задаваемые вопросы (FAQ)

1. Почему при нагревании металл хуже проводит ток, а полупроводник — лучше?

В металлах уже есть море свободных электронов. При нагреве атомы решетки начинают сильнее колебаться и чаще «сталкиваются» с электронами, мешая их движению (сопротивление растет). В полупроводниках свободных носителей изначально мало. Нагрев дает электронам энергию для выхода из валентной зоны в зону проводимости. Этот прирост количества носителей перекрывает эффект от колебаний решетки, поэтому проводимость резко возрастает.

2. Что такое «дырка» в физике полупроводников? Это реальная частица?

Дырка — это квазичастица. Физически это пустое место (вакансия) в электронной оболочке атома, откуда ушел электрон. Поскольку это место имеет нескомпенсированный положительный заряд ядра, оно притягивает соседние электроны. Перемещение электронов на вакантные места выглядит так, будто движется сам положительный заряд. Для расчетов удобно считать дырку реальной частицей с положительным зарядом.

3. Может ли диэлектрик стать проводником?

Да, может. Это происходит при явлении электрического пробоя. Если подать очень высокое напряжение, энергия поля станет достаточной, чтобы насильно вырвать электроны из атомов даже через широкую запрещенную зону. Материал теряет изолирующие свойства, часто с физическим разрушением (прожиг, искра).

4. Почему провода гудят под напряжением?

Гул (обычно 50 Гц) вызывается не самим движением электронов, а магнитострикцией и электростатическими силами. Переменное магнитное поле заставляет металлические сердечники трансформаторов и сами провода микроскопически сжиматься и разжиматься, порождая звуковую волну в воздухе.

5. Верно ли, что ток течет от плюса к минусу?

Исторически принято считать, что ток течет от плюса к минусу (так решили до открытия электрона). В реальности в металлах отрицательно заряженные электроны движутся от минуса к плюсу. В жидкостях и газах могут двигаться и положительные ионы (к минусу), и отрицательные (к плюсу) одновременно. Для инженерных расчетов историческая условность «плюс → минус» сохраняется, так как это не влияет на результат уравнений.

Заключение

Зонная теория твердого тела — это триумф человеческого разума, позволивший связать абстрактные уравнения квантовой механики с работой бытовой розетки и смартфона. Она объясняет, что электрический ток — это не просто поток шариков по трубе, а сложное волновое движение в периодическом потенциале.

Мы выяснили, что разделение на проводники, полупроводники и диэлектрики обусловлено шириной запрещенной энергетической зоны. Мы также установили, что реальное сопротивление проводников определяется дефектами кристаллической решетки: как врожденными (примеси), так и приобретенными (деформация, нагрев).

Нормативная база

ГОСТ 859-2014 «Медь. Марки». Определяет химический состав и чистоту меди, используемой в электротехнике.
ГОСТ 11069-2019 «Алюминий первичный. Марки». Аналогичный стандарт для алюминия.

Список литературы

Киттель, Ч. Введение в физику твердого тела / Ч. Киттель. — М.: Наука, 1978. — 792 с.
(Классический учебник, подробно описывающий теорию зон и свойства кристаллов).
Пасынков, В. В. Материалы электронной техники: учебник / В. В. Пасынков, В. С. Сорокин. — 6-е изд., стер. — СПб.: Лань, 2010. — 400 с.
(Базовый учебник для инженеров, связывающий физику с конкретными электротехническими материалами).
Савельев, И. В. Курс общей физики. В 3 т. Том 3. Квантовая оптика. Атомная физика. Физика твердого тела / И. В. Савельев. — СПб.: Лань, 2019. — 320 с.
(Фундаментальный курс, где доступным языком объясняются основы квантовой механики и уравнений Шредингера).