Законы Ома и Кирхгофа в комплексной форме: Теория и расчет

Содержание страницы

1. Последовательная RLC-цепь: Закон Ома и второй закон Кирхгофа
2. Пример практического расчета (Последовательная цепь)
3. Параллельная RLC-цепь: Первый закон Кирхгофа и проводимости
4. Сравнение методов расчета
5. Пример сложного расчета (Параллельная цепь)
6. Преимущества и недостатки символического метода
7. Интересные факты об электротехнике и комплексных числах
8. FAQ: Часто задаваемые вопросы
Заключение

Что это? Это метод анализа электрических цепей переменного тока, при котором синусоидальные величины (ток и напряжение) заменяются комплексными числами (векторами или фазорами). Это позволяет свести сложные дифференциальные уравнения к простым алгебраическим, аналогичным расчету цепей постоянного тока.

Краткая история: Метод был предложен в 1893 году выдающимся инженером Чарльзом Протеусом Штейнмецем. Его революционная идея позволила инженерам рассчитывать сложные системы переменного тока (AC), что стало решающим фактором в победе переменного тока над постоянным в «Войне токов».

1. Последовательная RLC-цепь: Закон Ома и второй закон Кирхгофа

Рассмотрим последовательную цепь, состоящую из резистора $ R $, катушки индуктивности $ L $ и конденсатора $ C $. Если через такую цепь протекает синусоидальный ток:

i(t) = I_m \sin(\omega t + \psi_i)

То, как было установлено в теории электрических цепей, мгновенные значения напряжений на каждом элементе будут следующими:

На резисторе: Напряжение совпадает по фазе с током.
$ u_R = R \cdot i = R I_m \sin(\omega t + \psi_i) = U_{Rm} \sin(\omega t + \psi_i) $.
На катушке индуктивности: Напряжение опережает ток на $ 90^\circ $ ($ \pi/2 $).
$ u_L = L \frac{di}{dt} = \omega L I_m \cos(\omega t + \psi_i) = U_{Lm} \sin(\omega t + \psi_i + \frac{\pi}{2}) $.
На конденсаторе: Напряжение отстает от тока на $ 90^\circ $ ($ \pi/2 $).
$ u_C = \frac{1}{C} \int i \, dt = \frac{I_m}{\omega C} (-\cos(\omega t + \psi_i)) = U_{Cm} \sin(\omega t + \psi_i — \frac{\pi}{2}) $.

Амплитуды напряжений определяются как:
$ U_{Rm} = R I_m $; $ U_{Lm} = \omega L I_m = X_L I_m $; $ U_{Cm} = \frac{I_m}{\omega C} = X_C I_m $.

Действующие значения соответственно равны:
$ U_R = R I $; $ U_L = X_L I $; $ U_C = X_C I $.

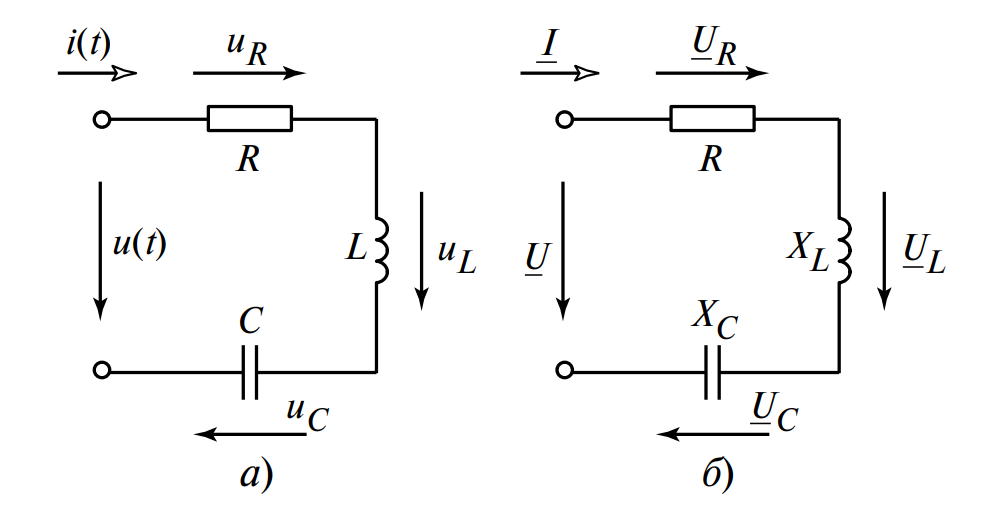
Напряжения и ток в последовательной RLC-цепи и векторная диаграмма

а) Схема цепи: Источник напряжения $ u(t) $, резистор $ R $, катушка $ L $, конденсатор $ C $ соединены последовательно. Ток $ i $ общий.
б) Векторная диаграмма напряжений: Вектор $ U_R $ совпадает с током, $ U_L $ направлен вверх (+90°), $ U_C $ направлен вниз (-90°).

Рис. 1. Напряжения и ток в последовательной RLC-цепи (а) и векторная диаграмма (б).

Переход к комплексной форме

Для упрощения расчетов перейдем от временных функций к комплексным амплитудам. Учитывая, что умножение на мнимую единицу $ j $ соответствует повороту вектора на $ +90^\circ $ ($ e^{j\pi/2} = j $), а $ -j $ — на $ -90^\circ $ ($ e^{-j\pi/2} = -j $):

\underline{U}_{Rm} = R \underline{I}_m \) \( \underline{U}_{Lm} = \omega L I_m e^{j(\psi_i + \pi/2)} = j \omega L \underline{I}_m = j X_L \underline{I}_m \) \( \underline{U}_{Cm} = \frac{1}{\omega C} I_m e^{j(\psi_i — \pi/2)} = -j \frac{1}{\omega C} \underline{I}_m = -j X_C \underline{I}_m

Аналогичные соотношения справедливы и для комплексных действующих значений напряжений:

\underline{U}_R = R \underline{I} \); \quad \( \underline{U}_L = j \omega L \underline{I} = j X_L \underline{I} \); \quad \( \underline{U}_C = \frac{1}{j \omega C} \underline{I} = -j X_C \underline{I}

По второму закону Кирхгофа для мгновенных значений сумма падений напряжений равна ЭДС источника:

\( u = u_R + u_L + u_C \)

Записав это уравнение в комплексной форме для действующих значений, получаем:

\underline{U} = \underline{U}_R + \underline{U}_L + \underline{U}_C = R \underline{I} + j \omega L \underline{I} — j \frac{1}{\omega C} \underline{I}

Вынесем ток $ \underline{I} $ за скобки:

\underline{U} = \left[ R + j \left( \omega L — \frac{1}{\omega C} \right) \right] \underline{I} = \left[ R + j(X_L — X_C) \right] \underline{I}

Закон Ома в комплексной форме

Из полученного уравнения следует закон Ома для цепи переменного тока:

\underline{I} = \frac{\underline{U}}{\underline{Z}}

Где $ \underline{Z} $ — комплексное сопротивление последовательной RLC-цепи:

$ X_L = \omega L $ — индуктивное сопротивление;
$ X_C = \frac{1}{\omega C} $ — емкостное сопротивление;
$ X = X_L — X_C $ — реактивное сопротивление;
$ R $ — активное сопротивление;
$ Z = \sqrt{R^2 + X^2} $ — модуль полного сопротивления (импеданс);
$ \phi = \text{arctg}\frac{X}{R} $ — аргумент комплексного сопротивления (угол сдвига фаз).

Аналогия для понимания: Представьте, что вы идете к цели. Активное сопротивление $ R $ — это путь прямо на восток. Индуктивное $ X_L $ — путь строго на север, а емкостное $ X_C $ — строго на юг. Реактивное сопротивление $ X $ — это итоговое смещение по оси «север-юг». Полное сопротивление $ Z $ — это расстояние по прямой от старта до финиша (гипотенуза).

2. Пример практического расчета (Последовательная цепь)

Задача: В неидеальной катушке, индуктивность которой равна 12 мГн, а активное сопротивление 9 Ом, протекает ток $ i(t) = 2 \sin(1000t) $ А (см. рис. 2, а). Чему равно мгновенное значение приложенного напряжения?

а) Схема замещения катушки: последовательно соединенные $ R $ и $ L $.
б) Комплексная схема: резистор с сопротивлением $ R $ и реактивный элемент $ j\omega L $.

Рис. 2. Напряжение и ток в неидеальной катушке

Решение: Применим символический метод.

Перейдем к комплексной схеме на частоте $ \omega = 1000 $ рад/с.
Рассчитаем комплексное сопротивление катушки: $$ \underline{Z} = R + j\omega L = 9 + j(1000 \cdot 12 \cdot 10^{-3}) = 9 + j12 $ Ом.$
Переведем в показательную форму:
$ |Z| = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15 $ Ом.
$ \phi = \text{arctg}(12/9) \approx 53,13^\circ $.
Итого: $ \underline{Z} = 15 \angle 53,13^\circ $ Ом.
Комплексная амплитуда тока:
Так как начальная фаза тока равна 0, то $ \underline{I}_m = 2 \angle 0^\circ = 2 $ А.
Найдем комплексную амплитуду напряжения по закону Ома: $$ \underline{U}_m = \underline{Z} \cdot \underline{I}_m = (15 \angle 53,13^\circ) \cdot 2 = 30 \angle 53,13^\circ $ В.$
Запишем мгновенное значение напряжения (возвращаемся во временную область):
$ u(t) = 30 \sin(1000t + 53,13^\circ) $ В.

3. Параллельная RLC-цепь: Первый закон Кирхгофа и проводимости

При анализе цепей с параллельным соединением элементов (рис. 3) удобнее оперировать не сопротивлениями, а проводимостями.

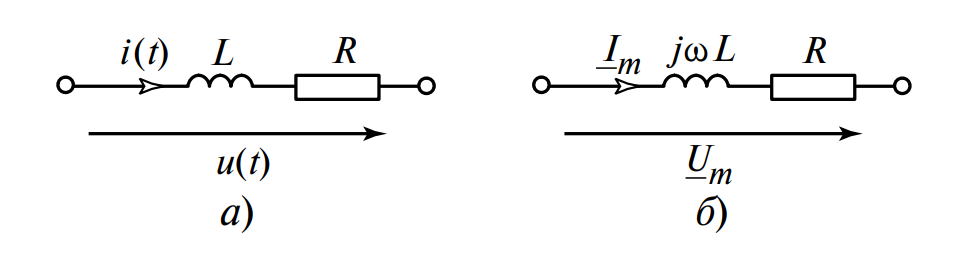
а) Схема цепи: Элементы $ R $, $ L $ и $ C $ подключены параллельно к источнику $ u $. Ток $ i $ разветвляется на $ i_R, i_L, i_C $.
б) Схема с проводимостями: Представление элементов через $ G $, $ B_L $, $ B_C $.

Рис. 3. Напряжение и токи в цепи с параллельным соединением элементов R, L, C

Пусть напряжение на входе $ u = U_m \sin(\omega t + \psi_u) $ представлено комплексным действующим значением $ \underline{U} $. Токи в ветвях определяются следующим образом:

\underline{I}_R = \frac{\underline{U}}{R} = G \underline{U} \) \( \underline{I}_L = \frac{\underline{U}}{j\omega L} = \frac{\underline{U}}{j X_L} = -j B_L \underline{U} \) \( \underline{I}_C = \frac{\underline{U}}{1/(j\omega C)} = j \omega C \underline{U} = j B_C \underline{U}

Где:

$ G = 1/R $ — активная проводимость;
$ B_L = \frac{1}{\omega L} $ — индуктивная проводимость;
$ B_C = \omega C $ — емкостная проводимость.

По первому закону Кирхгофа сумма токов в узле равна нулю (или входящий ток равен сумме исходящих):

\underline{I} = \underline{I}_R + \underline{I}_L + \underline{I}_C = (G — j B_L + j B_C) \underline{U} = [G + j(B_C — B_L)] \underline{U}

Отсюда получаем выражение для полной комплексной проводимости $ \underline{Y} $:

\underline{Y} = G — j(B_L — B_C) = G + j B_{\text{рез}}

(Примечание: Знак перед мнимой частью зависит от того, что считать результирующей реактивной проводимостью $ B $. Обычно принимают $ B = B_C — B_L $ или наоборот, важно следить за знаками токов). В исходном выражении принято:

\underline{I} = \underline{Y} \underline{U}

Модуль полной проводимости: $ Y = \sqrt{G^2 + (B_L — B_C)^2} $.

Важно помнить: Величины $ B_L $ и $ B_C $ сами по себе положительны. Реактивная проводимость цепи $ B $ — величина алгебраическая и может быть как положительной (емкостный характер), так и отрицательной (индуктивный характер).

4. Сравнение методов расчета

Характеристика	Последовательная RLC-цепь	Параллельная RLC-цепь
Основной закон	II закон Кирхгофа (сумма напряжений)	I закон Кирхгофа (сумма токов)
Ключевой параметр	Импеданс (Сопротивление) $ \underline{Z} $	Адмиттанс (Проводимость) $ \underline{Y} $
Общий параметр	Ток $ \underline{I} $ одинаков для всех	Напряжение $ \underline{U} $ одинаково для всех
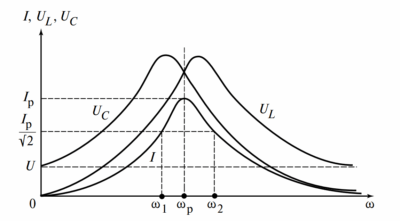
Резонанс	Резонанс напряжений ($ U_L = U_C $)	Резонанс токов ($ I_L = I_C $)
Формула	$ \underline{Z} = R + j(\omega L — \frac{1}{\omega C}) $	$ \underline{Y} = G + j(\omega C — \frac{1}{\omega L}) $

5. Пример сложного расчета (Параллельная цепь)

Пример 1. Сопротивление $ R $ неидеального конденсатора постоянному току равно 10 кОм (утечка). При переменном токе частотой $ f_1 = 1600 $ Гц известен тангенс угла потерь $ \text{tg} \, \delta = 0,05 $. Для параллельной схемы замещения конденсатора определить $ \text{tg} \, \delta $, полную мощность $ S $, активную $ P $ и реактивную $ Q $ при новой частоте $ f_2 = 3200 $ Гц и напряжении $ U = 380 $ В. Активное сопротивление считать постоянным.

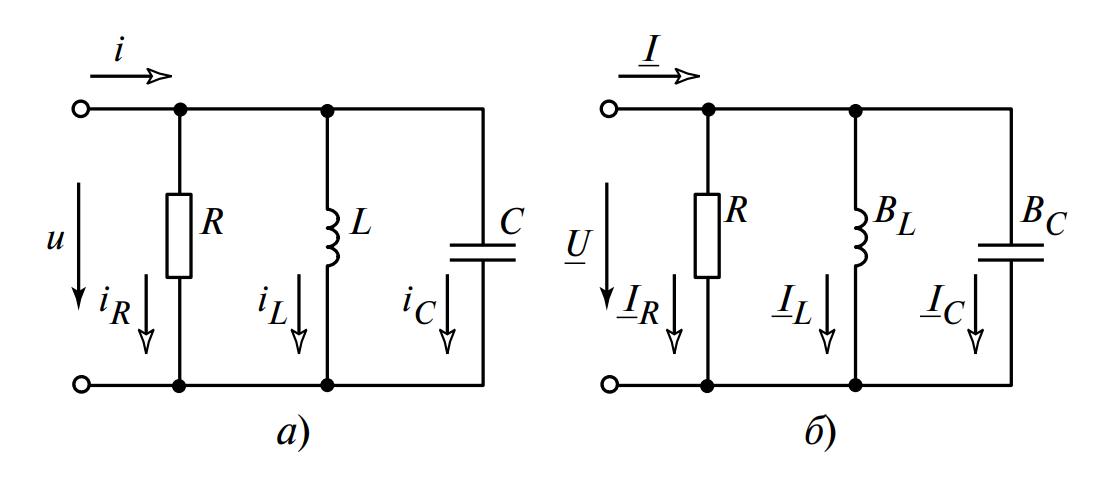
а) Параллельная схема замещения конденсатора: Резистор утечки $ R $ параллельно с идеальной емкостью $ C $.
б) Векторная диаграмма токов: Активный ток $ I_R $ совпадает с напряжением $ U $, емкостный ток $ I_C $ опережает на 90°. Угол $ \delta $ дополняет фазовый сдвиг до 90°.

Рис. 4. Параллельная схема замещения конденсатора (а) и векторная диаграмма (б)

Решение:

Найдем емкость конденсатора.
Для параллельной схемы замещения $ \text{tg} \, \delta = \frac{I_R}{I_C} = \frac{U/R}{U \omega C} = \frac{1}{R \omega C} $.
На частоте $ f_1 = 1600 $ Гц:
$C = \frac{1}{R \cdot 2\pi f_1 \cdot \text{tg} \, \delta} = \frac{1}{10^4 \cdot 2\pi \cdot 1600 \cdot 0,05} \approx 0,198 \cdot 10^{-6} \text{ Ф} = 0,198 \text{ мкФ}.$
Расчет на новой частоте $ f_2 = 3200 $ Гц.
Так как частота увеличилась в 2 раза, а $ R $ и $ C $ неизменны, новый угол потерь:
$\text{tg} \, \delta_2 = \frac{1}{R \cdot 2\pi f_2 \cdot C} = \frac{1}{10^4 \cdot 2\pi \cdot 3200 \cdot 0,198 \cdot 10^{-6}} \approx 0,025.$
(Тангенс уменьшился в 2 раза).
Расчет мощностей при $ U = 380 $ В.
Активная мощность (рассеивается на R):
$P = \frac{U^2}{R} = \frac{380^2}{10000} = 14,44 \text{ Вт}.$
Реактивная мощность (на C):
$Q = U^2 \omega_2 C = 380^2 \cdot (2\pi \cdot 3200) \cdot 0,198 \cdot 10^{-6} \approx 577,6 \text{ ВАр}.$
Полная мощность:
$S = \sqrt{P^2 + Q^2} = \sqrt{14,44^2 + 577,6^2} \approx 577,8 \text{ ВА}.$

6. Преимущества и недостатки символического метода

Преимущества:
- Замена интегро-дифференциальных уравнений простыми алгебраическими.
- Возможность использования векторных диаграмм для наглядности.
- Универсальность законов Ома и Кирхгофа (работают как для DC, так и для AC).
Недостатки:
- Применим только для линейных цепей.
- Работает только для установившегося синусоидального режима (не подходит для переходных процессов без применения преобразования Лапласа).
- Требует знаний алгебры комплексных чисел.

7. Интересные факты об электротехнике и комплексных числах

1. Магия «J»: Электротехники используют букву $ j $ для мнимой единицы вместо математической $ i $, чтобы не путать её с символом мгновенного тока $ i(t) $.
2. Штейнмец — спаситель GE: Чарльз Штейнмец, внедривший этот метод, был горбатым карликом с гигантским интеллектом. Когда General Electric не могли починить генератор, он пришел, поставил мелом крестик на корпусе и выставил счет на $10,000. «1 доллар за мел, 9999 за знание, куда поставить».
3. Реальность мнимого: Хотя числа называются «мнимыми», реактивная мощность $ Q $, рассчитываемая с их помощью, вполне реальна — она греет провода, но не совершает полезной работы в нагрузке.
4. Эйлер всему голова: Формула $ e^{j\phi} = \cos \phi + j \sin \phi $, лежащая в основе метода, считается одной из самых красивых в математике.
5. Скин-эффект: На высоких частотах комплексное сопротивление провода меняется, так как ток вытесняется на поверхность. Обычный закон Ома $ U=IR $ здесь дает сбой без учета поля.
6. Резонанс-разрушитель: Если $ X_L = X_C $, сопротивление цепи падает до минимума (только R). В мощных сетях это может вызвать токи короткого замыкания и взрывы, хотя «на бумаге» все элементы целы.
7. 50 vs 60 Гц: Выбор частоты (омега в формулах) исторически случаен. Тесла хотел 60 Гц, немцы — 50 Гц. Это влияет на $ X_L $ и $ X_C $ во всем мире до сих пор.

8. FAQ: Часто задаваемые вопросы

1. Почему нельзя просто складывать амплитуды напряжений $ U_R + U_L + U_C $?

Потому что максимумы напряжений наступают в разное время. Когда на резисторе максимум, на конденсаторе может быть ноль. Складывать нужно векторы, учитывая сдвиг фаз.

2. Что такое $ j $ физически?

В контексте векторных диаграмм умножение на $ j $ — это оператор поворота вектора на 90 градусов против часовой стрелки. Физически это отражает сдвиг фазы сигнала на четверть периода.

3. В чем разница между Z и R?

$ R $ (активное сопротивление) безвозвратно преобразует энергию в тепло. $ Z $ (импеданс) включает в себя и $ R $, и реактивные элементы $ L, C $, которые накапливают и возвращают энергию, не расходуя её.

4. Можно ли применять эти формулы для несинусоидального тока?

Напрямую — нет. Но любой периодический сигнал можно разложить в ряд Фурье (сумму синусоид), и для каждой гармоники рассчитать цепь отдельно этим методом, а затем сложить результаты (метод наложения).

5. Зачем нужен «минус» в формуле для конденсатора?

Минус перед $ j $ (или $ 1/j $) показывает, что напряжение на конденсаторе отстает от тока на 90 градусов. У индуктивности оно опережает, поэтому там знак плюс.

Заключение

Символический метод расчета цепей переменного тока, основанный на законах Ома и Кирхгофа в комплексной форме, является фундаментальным инструментом современного инженера. Он позволяет элегантно обходить сложности дифференциального исчисления, превращая анализ динамических процессов в RLC-цепях в решение линейных алгебраических уравнений. Понимание природы активного и реактивного сопротивления, а также фазовых сдвигов, критически важно для проектирования любых систем — от простейших фильтров до глобальных энергосетей.

Нормативная база

При проектировании и оформлении схем следует руководствоваться действующими стандартами:

ГОСТ IEC 60050-131-2015 — Международный электротехнический словарь. Часть 113. Физика в электротехнике.
ГОСТ 2.702-2011 — ЕСКД. Правила выполнения электрических схем.
ГОСТ 2.723-68 — Обозначения условные графические в схемах. Катушки индуктивности, дроссели, трансформаторы.
ГОСТ 2.728-74 — Обозначения условные графические. Резисторы, конденсаторы.

Законы Ома и Кирхгофа в комплексной форме: Расчет цепей переменного тока