Векторные диаграммы и комплексные числа в электротехнике

Содержание страницы

1. Представление синусоидальных величин на комплексной плоскости
2. Связь временной и комплексной форм
3. Операции с векторами: сложение синусоид
4. Преимущества и недостатки метода комплексных амплитуд
5. Сравнительная таблица представлений
6. Примеры практических расчетов
7. Интересныех факты о методе комплексных диаграмм
8. Часто задаваемые вопросы (FAQ)
Заключение

Использование комплексных чисел в электротехнике — это не просто математическая абстракция, а фундаментальный инструмент, превращающий сложные интегро-дифференциальные уравнения цепей переменного тока в относительно простые алгебраические уравнения. Этот метод, популяризированный Чарльзом Стейнмецем в конце XIX века, является стандартом для инженерных расчетов установившихся режимов.

Анализ электрических цепей синусоидального тока требует эффективных математических инструментов для представления величин, изменяющихся во времени. Векторные диаграммы на комплексной плоскости обеспечивают наглядное и точное описание амплитуд и фазовых соотношений между токами и напряжениями.

1. Представление синусоидальных величин на комплексной плоскости

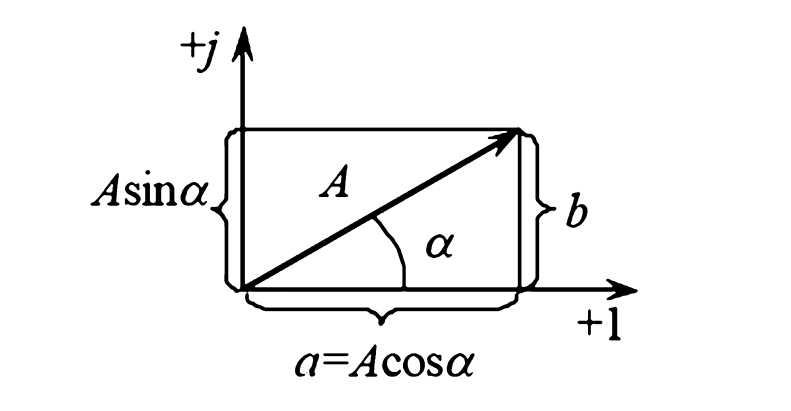
На комплексной плоскости (см. рис. 1) любой вектор может быть однозначно определен комплексным числом. В электротехнике для этого используются три основные формы записи:

Алгебраическая форма: удобна для сложения и вычитания векторов.
Тригонометрическая форма: наглядно демонстрирует связь с геометрическими проекциями.
Показательная (экспоненциальная) форма: идеальна для умножения, деления и возведения в степень.

Комплексное число $\dot{A}$ записывается следующим образом:

$$ \dot{A} = a + jb = A\cos\alpha + jA\sin\alpha = Ae^{j\alpha} $$

Где взаимосвязь параметров определяется формулами Эйлера и теоремой Пифагора:

$$ A = \sqrt{a^2 + b^2}, \quad \alpha = \text{arctg}\left(\frac{b}{a}\right) $$

Здесь $A$ — модуль комплексного числа (длина вектора), $\alpha$ — аргумент (угол наклона к действительной оси), $a$ — вещественная составляющая, $b$ — мнимая составляющая. В электротехнике мнимая единица обозначается буквой $j$ (чтобы не путать с током $i$), где $j^2 = -1$.

Рисунок демонстрирует комплексную плоскость с осями: горизонтальная Re (действительная, +1), вертикальная Im (мнимая, +j). Из начала координат выходит вектор A под углом $\alpha$ к оси Re. Его проекция на ось Re равна $a$, а на ось Im равна $b$. Показано, что $A = \sqrt{a^2 + b^2}$.

Рисунок 1 — Изображение комплексных величин на комплексной плоскости

1.1. Оператор поворота

Умножение комплексного числа на экспоненциальный множитель $e^{j\alpha}$ не изменяет его модуля, но приводит к изменению его аргумента. Геометрически это соответствует повороту вектора на угол $\alpha$ в положительном направлении (против часовой стрелки).

Важные частные случаи поворота вектора, используемые при анализе реактивных элементов (индуктивностей и емкостей):

Умножение на $j$ (или $e^{j\pi/2}$) поворачивает вектор на $+90^\circ$ (в сторону опережения).
Умножение на $-j$ (или $e^{-j\pi/2}$) поворачивает вектор на $-90^\circ$ (в сторону отставания).

1.2. Сопряженные комплексные числа

Два комплексных числа называются сопряженными, если они имеют равные модули и равные по величине, но противоположные по знаку аргументы. Если исходное число $\dot{A} = a + jb = Ae^{j\alpha}$, то сопряженное ему число обозначается звездочкой $\overset{*}{\dot{A}}$:

$$ \overset{*}{\dot{A}} = a — jb = Ae^{-j\alpha} $$

Произведение взаимно сопряженных чисел дает квадрат их модуля — всегда действительное положительное число:

$$ \dot{A} \cdot \overset{*}{\dot{A}} = A^2 $$

Важность сопряжения: В электроэнергетике сопряженные комплексы токов используются при вычислении полной комплексной мощности $ \dot{S} = \dot{U}\overset{*}{\dot{I}} $, что позволяет получить правильный знак для реактивной мощности $Q$.

2. Связь временной и комплексной форм

Аргумент комплексного числа может быть функцией времени: $\alpha(t) = \omega t + \psi$. В этом случае мы получаем вращающийся вектор (комплексную временную функцию):

$$ \dot{I}(t) = I_m e^{j(\omega t + \psi)} = I_m \cos(\omega t + \psi) + j I_m \sin(\omega t + \psi) $$

Мнимая часть этого выражения (обозначается оператором $Im[\cdot]$) полностью совпадает с уравнением мгновенного значения синусоидального тока:

$$ i(t) = I_m \sin(\omega t + \psi) = Im[I_m e^{j(\omega t + \psi)}] $$

При изменении времени $t$ вектор $\dot{I}(t)$ вращается на комплексной плоскости с угловой скоростью $\omega$ против часовой стрелки. Проекция этого вектора на мнимую ось в любой момент времени дает мгновенное значение физической величины.

2.1. Комплексная амплитуда и действующее значение

Поскольку в линейных цепях частота $\omega$ одинакова для всех токов и напряжений, все векторы вращаются синхронно, сохраняя взаимное расположение. Это позволяет «остановить» время (принять $t=0$) и оперировать неподвижными векторами.

Условная запись перехода от оригинала (функции времени) к изображению (комплексному числу) имеет вид:

$$ i(t) \leftrightarrow \dot{I}_m e^{j\omega t} \quad \text{(1)} $$

Комплексная амплитуда — это вектор, модуль которого равен амплитуде, а аргумент — начальной фазе:

$$ \dot{I}_m = I_m e^{j\psi} = I_m \cos\psi + j I_m \sin\psi \quad \text{(2)} $$

Однако в практических расчетах чаще используют комплексное действующее значение (или просто комплексный ток), так как именно действующие значения измеряются большинством приборов:

$$ \dot{I} = \frac{\dot{I}_m}{\sqrt{2}} = \frac{I_m}{\sqrt{2}}e^{j\psi} = Ie^{j\psi} = I\cos\psi + jI\sin\psi \quad \text{(3)} $$

Аналогично определяются комплексы напряжений и ЭДС:

$$ \dot{U} = Ue^{j\psi_u}; \quad \dot{E} = Ee^{j\psi_e} $$

3. Операции с векторами: сложение синусоид

Одно из главных преимуществ векторного метода — простота суммирования колебаний. Если необходимо сложить два синусоидальных тока одной частоты:

$$ i_\Sigma = i_1 + i_2 = I_{m1}\sin(\omega t + \psi_1) + I_{m2}\sin(\omega t + \psi_2) \quad \text{(4)} $$

Вместо громоздких тригонометрических преобразований достаточно сложить соответствующие им комплексные числа:

$$ \dot{I}_{m\Sigma} = \dot{I}_{m1} + \dot{I}_{m2} = (I_{m1}e^{j\psi_1}) + (I_{m2}e^{j\psi_2}) \quad \text{(5)} $$

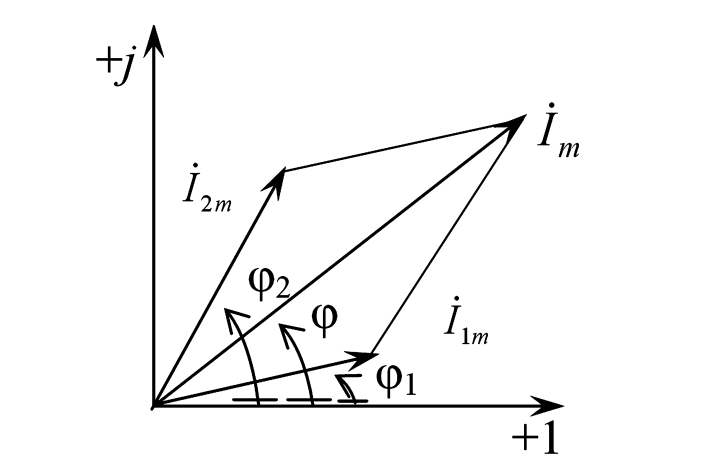
Результирующий вектор $\dot{I}_{m\Sigma}$ затем легко преобразуется обратно во временную форму. Геометрически это соответствует правилу параллелограмма (или треугольника) при сложении векторов.

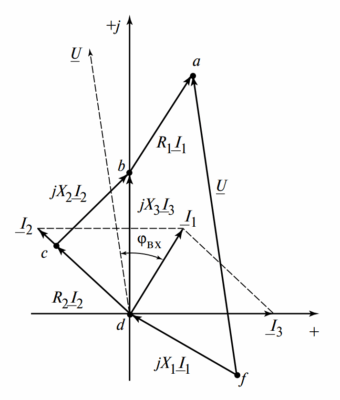
[Рисунок показывает сложение двух векторов на комплексной плоскости. Вектор I_m1 под углом $\psi_1$ и вектор I_m2 под углом $\psi_2$ складываются по правилу параллелограмма, образуя результирующий вектор I_{m\Sigma} с углом $\psi_\Sigma$.]

Рисунок 2 — Суммирование векторов на комплексной плоскости

4. Преимущества и недостатки метода комплексных амплитуд

Преимущества:

Алгебраизация задач: Дифференциальные уравнения переходят в алгебраические, что кардинально упрощает расчет цепей.
Наглядность: Векторные диаграммы позволяют визуально оценить фазовые сдвиги и соотношения величин.
Универсальность: Применим для расчета цепей любой сложности в установившемся режиме.

Недостатки и ограничения:

Только для линейных цепей: Метод некорректен при наличии нелинейных элементов, искажающих форму синусоиды.
Только установившийся режим: Не подходит для прямого расчета переходных процессов (для них используется операторный метод Лапласа).
Фиксированная частота: Все источники в расчитываемой подсхеме должны иметь одну частоту.

5. Сравнительная таблица представлений

Характеристика	Временная область (мгновенные значения)	Частотная область (комплексный метод)
Математическое представление	$ i(t) = I_m \sin(\omega t + \psi) $	$ \dot{I} = I e^{j\psi} $
Тип уравнений	Интегро-дифференциальные	Алгебраические (линейные)
Элемент индуктивности (L)	$ u_L = L \frac{di}{dt} $	$ \dot{U}_L = j\omega L \cdot \dot{I} $
Элемент емкости (C)	$ i_C = C \frac{du}{dt} $	$ \dot{I}_C = j\omega C \cdot \dot{U}_C $ или $ \dot{U}_C = \frac{\dot{I}}{j\omega C} $
Сложение сигналов	Сложные тригонометрические формулы	Сложение векторов: $ \dot{I}_\Sigma = \dot{I}_1 + \dot{I}_2 $

6. Примеры практических расчетов

Пример 3.1. Переход от комплексной формы к мгновенной

Дано: Комплекс действующего значения тока $ \dot{I} = 3 + j4 $ А. Частота сети стандартная (50 Гц, $\omega \approx 314$ рад/с).

Задание: Записать уравнение мгновенного значения тока $i(t)$.

Решение:

Найдем модуль действующего значения тока:
$$ I = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ А} $$
Найдем начальную фазу (аргумент):
$$ \psi = \text{arctg}\left(\frac{4}{3}\right) \approx 53,1^\circ $$
Комплекс тока в показательной форме: $ \dot{I} = 5e^{j53,1^\circ} $ А.
Амплитуда тока $ I_m = I \cdot \sqrt{2} = 5 \cdot 1,414 \approx 7,07 $ А.
Мгновенное значение:
$$ i(t) = 7,07 \sin(314t + 53,1^\circ) \text{ А} $$

Примечание: В исходном кратком условии использовалось упрощение $5\sqrt{2}$, которое можно оставить в символьном виде для точности.

Пример 3.2. Сложение напряжений

Дано: Мгновенные значения двух напряжений:
$ u_1(t) = 311\sin(314t + 30^\circ) $ В,
$ u_2(t) = 220\sin(314t + 45^\circ) $ В.

Задание: Определить суммарное напряжение $ u_\Sigma(t) $.

Решение:

Запишем комплексные амплитуды напряжений:
$$ \dot{U}_{m1} = 311e^{j30^\circ} = 311(\cos30^\circ + j\sin30^\circ) \approx 269,3 + j155,5 \text{ В} $$
$$ \dot{U}_{m2} = 220e^{j45^\circ} = 220(\cos45^\circ + j\sin45^\circ) \approx 155,6 + j155,6 \text{ В} $$
Сложим полученные комплексы (отдельно действительные и мнимые части):
$$ \dot{U}_{m\Sigma} = (269,3 + 155,6) + j(155,5 + 155,6) = 424,9 + j311,1 \text{ В} $$
Переведем результат обратно в показательную форму:
$$ U_{m\Sigma} = \sqrt{424,9^2 + 311,1^2} \approx 526,5 \text{ В} $$
$$ \psi_\Sigma = \text{arctg}\left(\frac{311,1}{424,9}\right) \approx 36,2^\circ $$
Итоговое мгновенное значение:
$$ u_\Sigma(t) = 526,5\sin(314t + 36,2^\circ) \text{ В} $$

7. Интересныех факты о методе комплексных диаграмм

Термин «мнимая»: Исторически сложившееся название «мнимая единица» для $j$ неудачно, так как в электротехнике мнимая составляющая отражает вполне реальную реактивную мощность, которая циркулирует в цепи, но не совершает полезной работы.
Почему J, а не I? В математике мнимая единица — это $i$. В электротехнике символ $i$ уже был занят для обозначения мгновенного тока, поэтому инженеры договорились использовать $j$.
Вектор или Фазор? Строго говоря, вращающийся вектор на комплексной плоскости в зарубежной литературе называют «фазором» (phasor — от phase vector), чтобы отличать его от пространственных векторов в механике.
Стейнмец — гений метода: Чарльз Стейнмец, внедривший этот метод, был горбуном с врожденными проблемами со здоровьем, но его математический гений позволил компании General Electric обойти конкурентов, которые не могли эффективно рассчитывать сложные цепи переменного тока.
Отрицательная частота: Математически, при использовании полной формулы Эйлера $\cos x = \frac{e^{jx} + e^{-jx}}{2}$, появляется понятие «отрицательной частоты», что имеет физический смысл при спектральном анализе сигналов.
Трехфазные системы: Векторные диаграммы незаменимы при анализе трехфазных цепей, позволяя мгновенно определить перекос фаз или обрыв нулевого провода графическим методом.
Связь с мощностью: На комплексной плоскости можно изображать не только токи и напряжения, но и сопротивления (треугольник сопротивлений) и мощности (треугольник мощностей), хотя они и не являются синусоидальными функциями времени в том же смысле.

8. Часто задаваемые вопросы (FAQ)

1. В чем разница между $\dot{I}_m$ и $\dot{I}$?

$\dot{I}_m$ — это комплексная амплитуда (длина вектора равна пиковому значению тока), а $\dot{I}$ — комплексное действующее значение (длина в $\sqrt{2}$ раз меньше). В расчетах мощности и потерь используют именно действующие значения.

2. Почему индуктивное сопротивление записывают как $jX_L$?

Множитель $j$ означает поворот на $+90^\circ$. Это отражает физический факт: напряжение на идеальной индуктивности опережает ток ровно на $90^\circ$.

3. Можно ли применять этот метод для несинусоидальных токов?

Напрямую — нет. Однако несинусоидальный сигнал можно разложить в ряд Фурье на сумму синусоид (гармоник) и применить комплексный метод для каждой гармоники отдельно.

4. Что такое «топографическая диаграмма»?

Это особый вид векторной диаграммы напряжений, где каждая точка на комплексной плоскости соответствует реальной точке электрической цепи. Она позволяет найти напряжение между любыми двумя точками схемы, просто измерив расстояние между ними на диаграмме.

5. Зависит ли векторная диаграмма от выбора начальной фазы?

Диаграмма может поворачиваться целиком в зависимости от того, какой вектор мы примем за базовый (с нулевой начальной фазой), но взаимное расположение векторов (углы между ними) останется неизменным.

6. Как связаны комплексные числа и показания мультиметра?

Обычный мультиметр показывает только модуль комплексного числа (действующее значение). Для определения фазового угла (аргумента) требуются более сложные приборы — фазометры или осциллографы.

7. Что произойдет, если перепутать $+j$ и $-j$?

Это приведет к грубой ошибке: индуктивность «превратится» в емкость, характер реактивной мощности изменится на противоположный, и расчет цепи будет полностью неверен.

Заключение

Метод комплексных амплитуд и векторных диаграмм является краеугольным камнем современной теоретической электротехники. Он позволяет инженерам переходить от сложных дифференциальных уравнений к наглядным геометрическим построениям и простым алгебраическим вычислениям. Глубокое понимание взаимосвязи между временным представлением сигнала и его образом на комплексной плоскости необходимо любому специалисту, работающему с цепями переменного тока, от проектирования энергосистем до разработки аналоговой электроники.

Нормативная база и литература

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий. (Действующий стандарт, устанавливающий корректную терминологию для векторных и комплексных величин).
ГОСТ 2.701-2008 — Единая система конструкторской документации (ЕСКД). Схемы. Виды и типы. Общие требования к выполнению.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2024.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Том 1. — Л.: Энергоиздат, 1981.