Содержание страницы
- 1. Трехфазная симметричная система ЭДС
- 2. Схемы соединения в трехфазных цепях
- 3. Расчет трехфазных цепей при симметричной нагрузке
- 4. Мощность трехфазной симметричной цепи
- 5. Несимметричные режимы в трехфазных цепях
- 6. Измерение мощности в трехфазных цепях
- Интересные факты о трехфазных системах
- FAQ: Часто задаваемые вопросы
- Заключение
Трехфазная цепь — это система производства, передачи и потребления электрической энергии переменного тока, состоящая из трех отдельных цепей (фаз), в которых действуют синусоидальные ЭДС (электродвижущие силы) одинаковой частоты и амплитуды. Ключевой особенностью является то, что эти ЭДС сдвинуты по фазе друг относительно друга на 120 градусов (или \( 2\pi/3 \) радиан).
В современной промышленности и в быту для электроснабжения потребителей используются преимущественно трехфазные цепи. Широкое распространение трехфазных систем объясняется главным образом тремя основными причинами:
- Экономичность. Передача энергии на дальние расстояния трехфазным током экономически более выгодна, чем переменным током с иным числом фаз. Например, для передачи той же мощности требуется 3 или 4 провода вместо 6 (для трех независимых однофазных систем).
- Эффективность оборудования. Элементы системы — трехфазный синхронный генератор, трехфазный асинхронный и синхронный двигатели, а также трехфазный трансформатор — конструктивно проще в производстве, более экономичны и надежны в работе по сравнению с однофазными аналогами.
- Стабильность мощности. Трехфазная система обладает свойством неизменности значения мгновенной мощности за период синусоидального тока, если нагрузка во всех трех фазах симметрична. Это обеспечивает плавную, без вибраций, работу электродвигателей.
Трехфазные цепи являются частным случаем разветвленных цепей, и их можно рассчитывать общими методами (например, методами контурных токов или узловых потенциалов). Однако для наиболее распространенных симметричных режимов существуют значительно более простые методы расчета.
1. Трехфазная симметричная система ЭДС
Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на 120°. Графики их мгновенных значений изображены на рисунке 1а, а векторная диаграмма — на рисунке 1б.
Принцип получения трехфазной системы ЭДС иллюстрирует рисунок 1в. В равномерном магнитном поле с постоянной угловой скоростью \( \omega \) вращаются три одинаковых, жестко скрепленных друг с другом катушки. Плоскости катушек смещены в пространстве друг относительно друга на 120°. В каждой катушке наводится синусоидальная ЭДС одинаковой амплитуды. По фазе ЭДС катушек оказываются сдвинуты на 120°. Аналогичным путем можно получить двух- и четырехфазную систему ЭДС и более. На практике наиболее распространена трехфазная система.
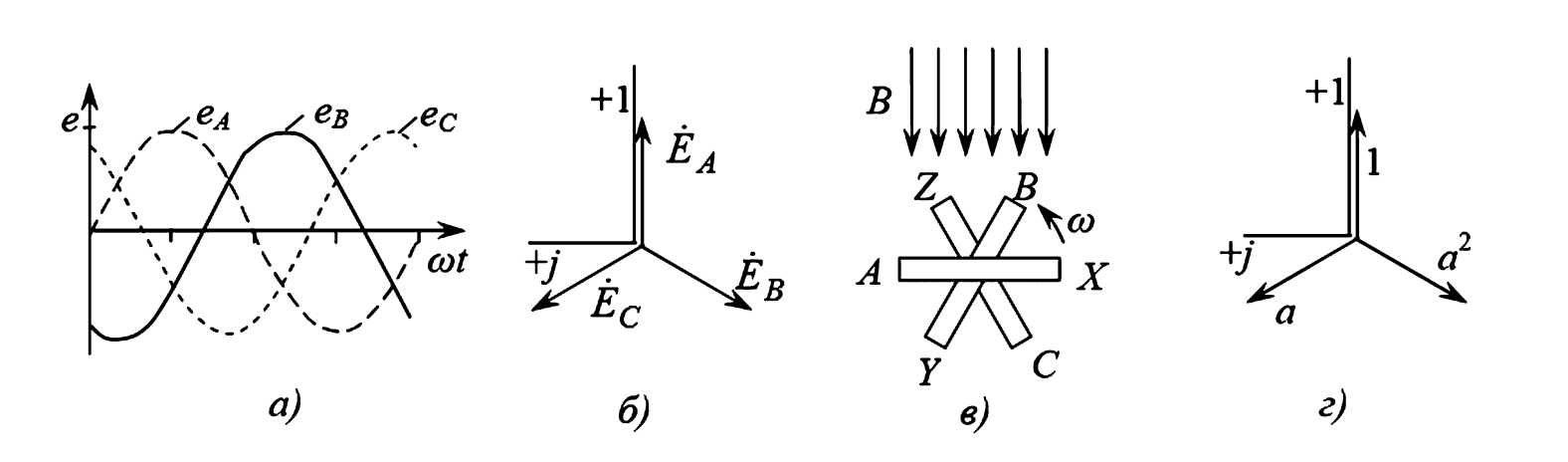
Рис. 1. Трехфазная система ЭДС: а — графики; б — векторная диаграмма; в — схема получения; г — операторы трехфазной системы.
ЭДС трехфазного генератора обозначают следующим образом: одну из ЭДС обозначают \( E_A \), на 120° отстающую от нее — \( E_B \), а \( E_C \) опережает \( E_A \) на 120° (что эквивалентно отставанию на 240°). Последовательность прохождения ЭДС через одинаковые значения (например, через нулевое значение при переходе в область положительных значений) называют последовательностью фаз. Стандартной является последовательность A-B-C.
1.1. Комплексное представление и оператор ‘a’
Для удобства расчетов синусоидальные величины представляют в виде комплексных чисел. Вводится специальный фазный оператор \( a \) — комплексное число, по модулю равное единице, с аргументом 120°:
$$ a = e^{j120^\circ} = 1 \angle 120^\circ = \cos(120^\circ) + j\sin(120^\circ) = -0.5 + j0.866 $$
Тогда:
$$ a^2 = e^{j240^\circ} = e^{-j120^\circ} = 1 \angle 240^\circ = -0.5 — j0.866 $$
$$ a^3 = e^{j360^\circ} = 1 $$
Три вектора (1, \( a \) и \( a^2 \)) образуют симметричную трехфазную систему (рис. 1г). Их сумма равна нулю, что является фундаментальным свойством симметричной системы:
$$ 1 + a + a^2 = 0 $$
Умножение какого-либо вектора (комплексного числа) на оператор \( a \) поворачивает его без изменения модуля на угол 120° против часовой стрелки. Умножение вектора на \( a^2 \) поворачивает его на угол 240° против часовой стрелки (или, что то же самое, поворачивает его по часовой стрелке на 120°).
С помощью оператора \( a \) можно выразить комплексные ЭДС \( \dot{E}_B \) и \( \dot{E}_C \) симметричной трехфазной системы через ЭДС \( \dot{E}_A \), принятую за базовую (с нулевой начальной фазой):
- \( \dot{E}_A = E \angle 0^\circ \)
- \( \dot{E}_B = \dot{E}_A \cdot a^2 = E \angle 0^\circ \cdot e^{-j120^\circ} = E \angle -120^\circ \) (отстает на 120°)
- \( \dot{E}_C = \dot{E}_A \cdot a = E \angle 0^\circ \cdot e^{j120^\circ} = E \angle +120^\circ \) (опережает на 120°)
Определение термина «фаза»: В электротехнике термин «фаза» имеет несколько значений. Это может быть:
- Аргумент синусоидально изменяющейся величины (например, «сдвиг по фазе»).
- Одна из обмоток генератора или нагрузки.
- Участок трехфазной цепи (совокупность проводов и оборудования), по которому протекает один и тот же фазный ток.
В дальнейшем под фазой будем понимать именно последний смысл, если не указано иное.
2. Схемы соединения в трехфазных цепях
Существуют различные способы соединения обмоток генератора с нагрузкой. Самым неэкономичным способом явилось бы соединение каждой обмотки генератора с нагрузкой двумя проводами, на что потребовалось бы шесть соединительных проводов. С целью экономии проводов и материалов обмотки трехфазного генератора и нагрузки соединяют по схеме «звезда» или по схеме «треугольник». При этом число соединительных проводов (линии электропередачи) от генератора к нагрузке уменьшается с шести до трех или четырех.
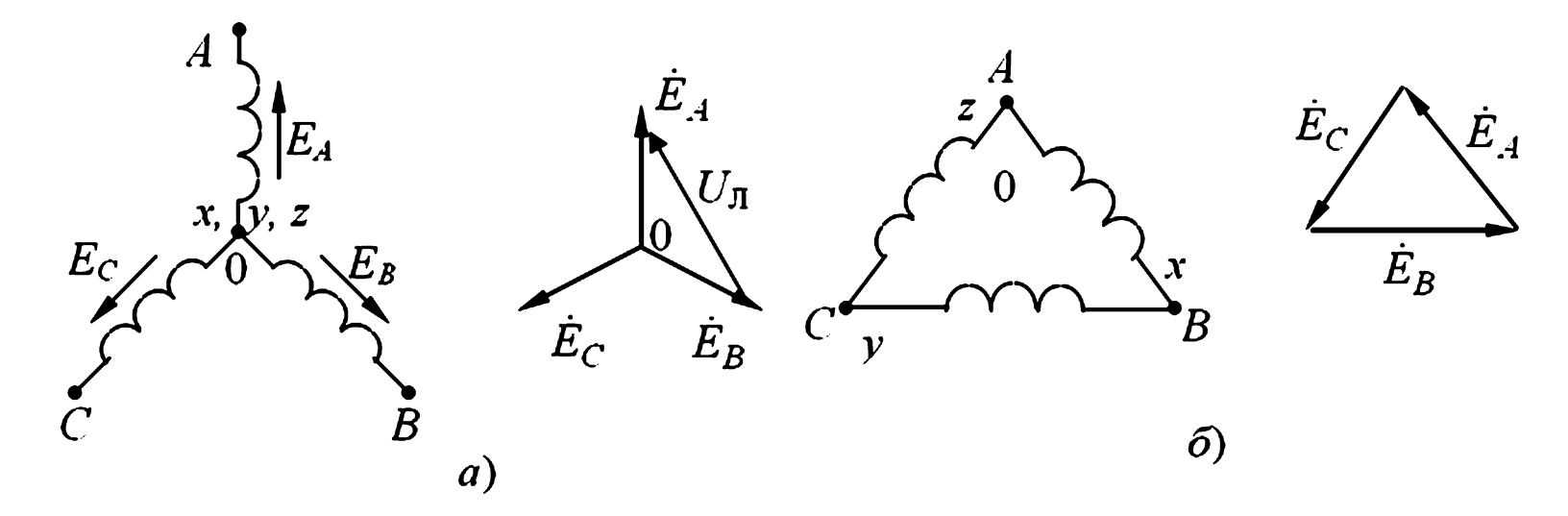
Рис. 2. Схемы соединений трехфазного генератора: а — «звезда»; б — «треугольник».
2.1. Соединение по схеме «Звезда» (Y)
На электрической схеме трехфазный генератор (или нагрузку) принято изображать в виде трех обмоток, расположенных друг к другу под углом 120°. При соединении по схеме «звезда» (рис. 2а) одноименные зажимы (например, концы обмоток X, Y, Z) трех обмоток объединяют в одну точку, которую называют нулевой (или нейтральной) точкой генератора и обозначают 0. Начала обмоток (A, B, C) подключаются к линии.
Нагрузку тоже можно включить по схеме «звезда». Точку, в которой объединены три конца трехфазной нагрузки, называют нулевой точкой нагрузки и обозначают 0′. Провод, соединяющий нулевые точки генератора (0) и нагрузки (0′), называют нулевым (или нейтральным) проводом. Ток в нем обозначают \( I_0 \). Такая система называется четырехпроводной. Если нейтральный провод отсутствует, система трехпроводная.
Провода, соединяющие точки A, B, C генератора с нагрузкой, называют линейными. Токи в линейных проводах называют линейными; их обозначают \( I_A, I_B, I_C \). Их модуль часто обозначают \( I_Л \). Напряжение между линейными проводами (например, \( U_{AB} \), \( U_{BC} \), \( U_{CA} \)) называют линейным; его модуль обозначают \( U_Л \). Напряжение между линейным и нейтральным проводом (например, \( U_{A0} \), \( U_{B0} \), \( U_{C0} \)) называют фазным; его модуль \( U_Ф \).
Для симметричной системы «звезда» справедливы следующие соотношения:
- Линейный ток равен фазному току: \( I_Л = I_Ф \).
- Линейное напряжение в \( \sqrt{3} \) раз больше фазного: \( U_Л = \sqrt{3} \cdot U_Ф \).
Последнее следует из векторного сложения. Например, \( \dot{U}_{AB} = \dot{U}_{A0} — \dot{U}_{B0} \). Из векторной диаграммы (равнобедренный треугольник с углом 120° при вершине) следует, что \( U_Л \) (основание) равно:
$$ U_Л = 2 \cdot U_Ф \cdot \cos(30^\circ) = 2 \cdot U_Ф \cdot (\sqrt{3}/2) = \sqrt{3} \cdot U_Ф $$
В основу формирования ряда трехфазных напряжений положен коэффициент \( \sqrt{3} \approx 1,732 \). Например: \( 127 \text{ В} \cdot \sqrt{3} \approx 220 \text{ В} \); \( 220 \text{ В} \cdot \sqrt{3} \approx 380 \text{ В} \); \( 380 \text{ В} \cdot \sqrt{3} \approx 660 \text{ В} \).
Согласно межгосударственному стандарту ГОСТ 29322-2014 (IEC 60038:2009) «Напряжения стандартные», рекомендованным стандартным напряжением для сетей низкого напряжения является 230/400 В (фазное/линейное), что является результатом эволюции систем 220/380 В. Однако системы 220/380 В продолжают широко применяться.
Нормы качества электроэнергии, включая допустимые отклонения напряжения (обычно ±10% от номинального), устанавливаются ГОСТ 32144-2013.
2.2. Соединение по схеме «Треугольник» (Δ)
При соединении обмоток генератора по схеме «треугольник» (рис. 2б) конец первой обмотки генератора (X) соединяют с началом второй (B), конец второй (Y) — с началом третьей (C), конец третьей (Z) — с началом первой (A). Линейные провода подключаются к точкам соединения (узлам A, B, C).
В симметричной системе геометрическая (векторная) сумма ЭДС в замкнутом треугольнике равна нулю ( \( \dot{E}_{AB} + \dot{E}_{BC} + \dot{E}_{CA} = 0 \) ). Поэтому, если к зажимам A, B, C не присоединена нагрузка (режим холостого хода), ток по обмоткам генератора протекать не будет (отсутствует уравнительный ток).
Для симметричной системы «треугольник» справедливы следующие соотношения:
- Линейное напряжение равно фазному: \( U_Л = U_Ф \).
- При симметричной нагрузке линейный ток в \( \sqrt{3} \) раз больше фазного: \( I_Л = \sqrt{3} \cdot I_Ф \).
Линейные токи определяются по первому закону Кирхгофа для узлов A, B, C. Например, для узла A:
$$ \dot{I}_A = \dot{I}_{AB} — \dot{I}_{CA} $$
При симметричной нагрузке векторная разность этих токов дает модуль \( I_Л \), который в \( \sqrt{3} \) раз больше \( I_Ф \).
2.3. Сравнение схем «Звезда» и «Треугольник»
Выбор схемы соединения зависит от конкретной задачи, напряжения сети и параметров нагрузки.
| Характеристика | Схема «Звезда» (Y) | Схема «Треугольник» (Δ) |
|---|---|---|
| Соотношение напряжений | \( U_Л = \sqrt{3} \cdot U_Ф \) | \( U_Л = U_Ф \) |
| Соотношение токов (симм. нагрузка) | \( I_Л = I_Ф \) | \( I_Л = \sqrt{3} \cdot I_Ф \) |
| Нейтральный провод | Возможен (4-проводная система) | Отсутствует (3-проводная система) |
| Преимущества | Два уровня напряжения (U_Ф и U_Л). Возможность подключения несимметричной нагрузки (при наличии нейтрали). | Выше надежность (возможна работа в «открытом треугольнике»). Выше фазные токи (при том же U_Л). |
| Недостатки | Опасность «смещения нейтрали» при обрыве нуля и несимметрии. | Только один уровень напряжения. Чувствительность к несимметрии ЭДС (уравнительные токи). |
| Применение | Сети 0.4 кВ (220/380 В), осветительные сети, смешанная нагрузка. | Двигатели, нагреватели, высоковольтные сети (для снижения фазного напряжения). |
Возможны пять основных способов соединения трехфазного генератора с трехфазной нагрузкой: «звезда — звезда» с нулевым проводом (Y–Y), «звезда — звезда» без нулевого провода (Y–Y), «звезда — треугольник» (Y–Δ); «треугольник — треугольник» (Δ–Δ), «треугольник — звезда» (Δ–Y).
3. Расчет трехфазных цепей при симметричной нагрузке
Симметричный режим является основным и наиболее желательным. В этом режиме комплексные сопротивления всех трех фаз нагрузки одинаковы: \( Z_A = Z_B = Z_C = Z_Ф \). Расчет такой системы значительно упрощается.
3.1. Схема «Звезда — звезда» (Y–Y)
Рассмотрим схему (рис. 3) с нейтральным проводом. Из-за полной симметрии (симметрия ЭДС и симметрия нагрузки), токи в фазных проводах (\( \dot{I}_А, \dot{I}_В, \dot{I}_С \)) будут одинаковы по значению и последовательно смещены по фазе на 120°, т. е.
$$ \dot{I}_B = \dot{I}_A \cdot a^2 \text{ (отстает на 120°)} $$
$$ \dot{I}_C = \dot{I}_A \cdot a \text{ (опережает на 120°)} $$
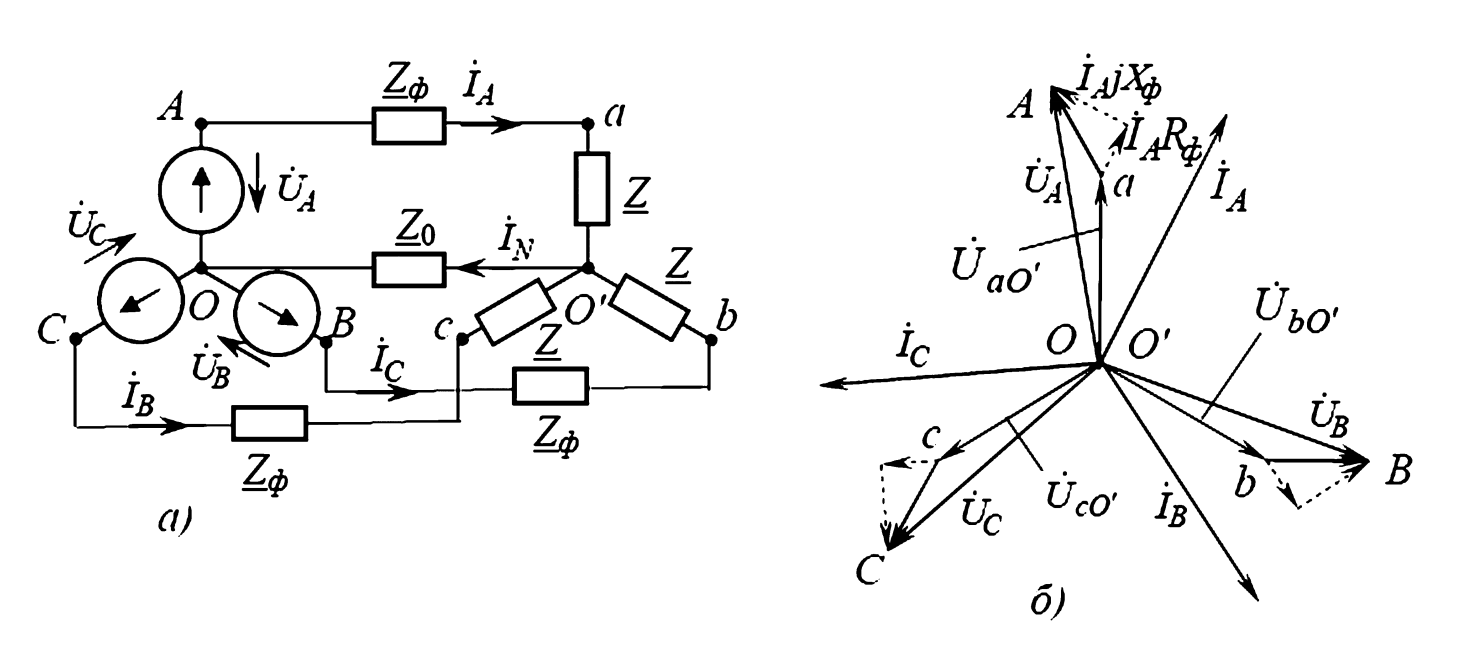
Рис. 3. Трехфазная цепь при симметричной нагрузке: а — схема; б — векторная диаграмма.
Ток в нулевом проводе \( \dot{I}_0 \) по первому закону Кирхгофа равен сумме трех фазных токов:
$$ \dot{I}_0 = \dot{I}_A + \dot{I}_B + \dot{I}_C = \dot{I}_A + \dot{I}_A \cdot a^2 + \dot{I}_A \cdot a = \dot{I}_A (1 + a^2 + a) $$
Поскольку \( 1 + a + a^2 = 0 \), то при симметричной нагрузке ток в нейтральном проводе равен нулю: \( \dot{I}_0 = 0 \).
Если это так, то потенциалы точек 0 и 0′ совпадают. Следовательно, полное фазное напряжение генератора \( \dot{U}_Ф \) (например, \( \dot{U}_{A0} \)) подается на последовательно включенные сопротивления фазы нагрузки \( Z_Ф \) и линии \( Z_Л \). По закону Ома:
$$ \dot{I}_A = \frac{\dot{U}_{A0}}{Z_{линии} + Z_Ф} \quad \dot{I}_B = \frac{\dot{U}_{B0}}{Z_{линии} + Z_Ф} $$
Это позволяет вести расчет для одной фазы (метод однофазного эквивалента), как будто это обычная однофазная цепь (рис. 4). В других фазах токи и напряжения будут такие же по модулю, но сдвинуты на ±120°.
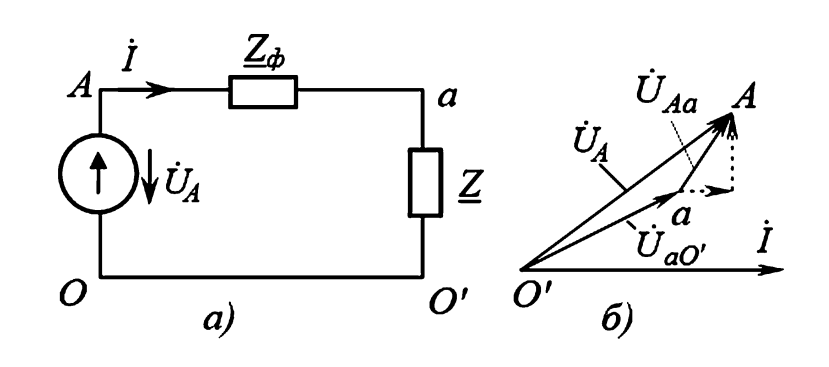
Рис. 4. Расчет на одну фазу: а — схема цепи; б — векторная диаграмма.
Отсутствие тока в нулевом проводе при симметричной нагрузке позволяет применять схемы «звезда — звезда» без нулевого провода (трехпроводные) для заведомо симметричной нагрузки (например, для питания трехфазных двигателей). Расчет такой цепи выполняется аналогично рассмотренному выше.
3.2. Схема с нагрузкой «Треугольник» (Δ)
При включении симметричной нагрузки по схеме «треугольник» (рис. 5а) напряжения на фазах нагрузки равны линейным напряжениям генератора: \( U_{ab} = U_{AB} = U_Л \). Тогда фазные токи в нагрузке равны:
$$ \dot{I}_{ab} = \frac{\dot{U}_{ab}}{Z_{ab}} \quad \dot{I}_{bc} = \frac{\dot{U}_{bc}}{Z_{bc}} \quad \dot{I}_{ca} = \frac{\dot{U}_{ca}}{Z_{ca}} $$
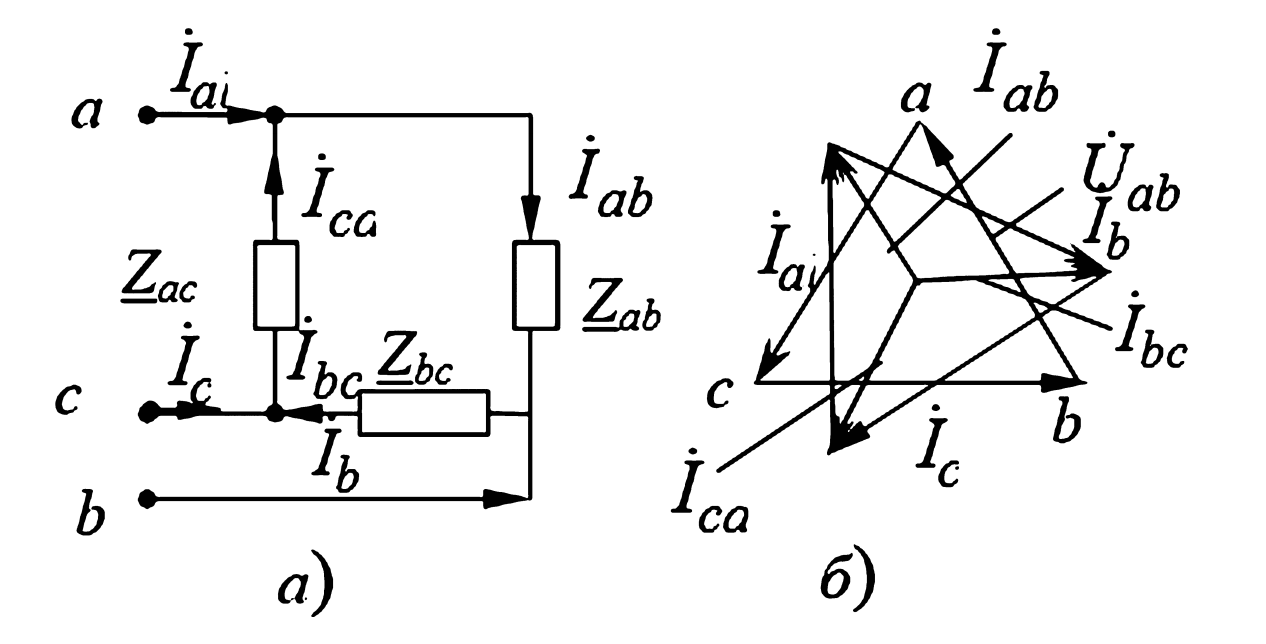
Рис. 5. Схема соединений треугольником: а — вариант графического изображения; б — векторная диаграмма.
Линейные токи определяются из векторной суммы фазных, например: \( \dot{I}_A = \dot{I}_{ab} — \dot{I}_{ca} \). Как было сказано, для симметричного режима \( I_Л = \sqrt{3} \cdot I_Ф \).
Для наглядности диаграмма (рис. 5б) построена для случая, когда сопротивления нагрузки активные (Z = R). Тогда фазные токи \( I_{ab}, I_{bc}, I_{ca} \) на диаграмме параллельны (совпадают по фазе) фазным напряжениям \( U_{ab}, U_{bc}, U_{ca} \). Линейные токи \( I_a, I_b, I_c \) определяются как разность фазных токов и образуют треугольник, повернутый относительно треугольника напряжений на 30°.
3.3. Расчет схемы «Треугольник» с учетом сопротивления линии
В тех случаях, когда сопротивлением линейных проводов \( Z_Л \) нельзя пренебречь (рис. 6), для расчета цепи применяют метод эквивалентного преобразования. Нагрузку, соединенную «треугольником» (\( Z_Δ \)), заменяют эквивалентной «звездой» (\( Z_Y \)).
При симметричной нагрузке сопротивление эквивалентной фазы «звезды» в 3 раза меньше сопротивления фазы «треугольника»:
$$ Z_Y = \frac{Z_Δ}{3} $$
После такой замены получается схема «звезда — звезда» (аналогичная рис. 3), которая, как показано выше, рассчитывается по методу одной фазы. При этом сразу определяются линейные токи \( I_a, I_b, I_c \). Фазные токи (в исходном треугольнике нагрузки) по модулю будут в \( \sqrt{3} \) раз меньше линейных и будут отставать от них на угол 30° (для стандартной последовательности фаз).
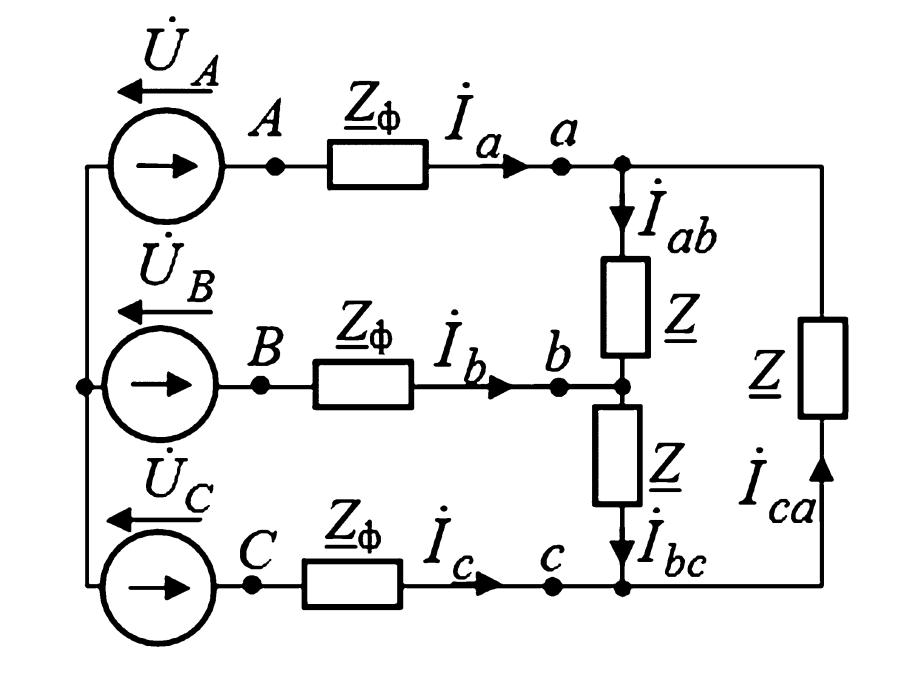
Рис. 6. Электрическая схема к примеру 1.
Пример 1
В цепи (рис. 6) линейное напряжение на зажимах генератора \( U_Л = 220 \text{ В} \), сопротивление линейных проводов \( Z_Л = 10 \text{ Ом} \), сопротивление фаз нагрузки \( Z_Δ = 30 — j30 \text{ Ом} \). Определить фазный ток в нагрузке \( I_{ab} \) и линейное напряжение на нагрузке \( U_{ab} \).
Решение:
- Заменим «треугольник» нагрузки на эквивалентную «звезду»:
$$ Z_Y = \frac{Z_Δ}{3} = \frac{30 — j30}{3} = 10 — j10 \text{ Ом} $$ - Полученную схему «звезда-звезда» ведем расчетом на одну фазу. Фазное напряжение генератора:
$$ U_{Ф(ген)} = \frac{U_Л}{\sqrt{3}} = \frac{220}{1.732} \approx 127 \text{ В} $$
Примем вектор \( \dot{U}_{A0} \) за базовый: \( \dot{U}_{A0} = 127 \angle 0^\circ \text{ В} \). - Суммарное сопротивление одной фазы (линия + нагрузка):
$$ Z_{общ} = Z_Л + Z_Y = 10 + (10 — j10) = 20 — j10 \text{ Ом} $$ - Определяем линейный ток (он же ток в эквивалентной звезде):
$$ \dot{I}_A = \frac{\dot{U}_{A0}}{Z_{общ}} = \frac{127 \angle 0^\circ}{20 — j10} $$
В полярной форме: \( 20 — j10 \text{ Ом} = 22.36 \angle -26.57^\circ \text{ Ом} \).
$$ \dot{I}_A = \frac{127 \angle 0^\circ}{22.36 \angle -26.57^\circ} \approx 5.68 \angle 26.57^\circ \text{ А} $$ - Определяем фазный ток \( \dot{I}_{ab} \) в исходном треугольнике. Его модуль в \( \sqrt{3} \) раз меньше линейного, а фаза отстает на 30°:
$$ I_{ab} = \frac{I_A}{\sqrt{3}} = \frac{5.68}{1.732} \approx 3.28 \text{ А} $$
$$ \phi_{ab} = \phi_A — 30^\circ = 26.57^\circ — 30^\circ = -3.43^\circ $$
Ответ 1: \( \dot{I}_{ab} \approx 3.28 \angle -3.43^\circ \text{ А} \). - Определяем линейное напряжение на нагрузке \( U_{ab} \). Сначала найдем фазное напряжение на эквивалентной звезде нагрузки:
$$ \dot{U}_{a’0′} = \dot{I}_A \cdot Z_Y = (5.68 \angle 26.57^\circ) \cdot (10 — j10) $$
В полярной форме: \( 10 — j10 \text{ Ом} = 14.14 \angle -45^\circ \text{ Ом} \).
$$ \dot{U}_{a’0′} = (5.68 \cdot 14.14) \angle (26.57^\circ — 45^\circ) \approx 80.3 \angle -18.43^\circ \text{ В} $$ - Линейное напряжение на нагрузке \( U_{ab} \) (которое равно фазному напряжению \( U_{ab} \) для треугольника) в \( \sqrt{3} \) раз больше фазного напряжения эквивалентной звезды:
$$ U_{ab} = U_{a’0′} \cdot \sqrt{3} = 80.3 \cdot 1.732 \approx 139.1 \text{ В} $$
Ответ 2: \( U_{ab} \approx 139.1 \text{ В} \).
4. Мощность трехфазной симметричной цепи
При симметричной нагрузке мощности во всех трех фазах одинаковы. Полная мощность цепи равна утроенной мощности одной фазы.
Комплексная мощность одной фазы:
$$ \tilde{S}_Ф = \dot{U}_Ф \cdot \dot{I}_Ф^* = U_Ф I_Ф (\cos\phi + j\sin\phi) = P_Ф + jQ_Ф $$
где \( \phi \) — это угол сдвига фаз между фазным напряжением \( \dot{U}_Ф \) и фазным током \( \dot{I}_Ф \). \( \dot{I}_Ф^* \) — комплексно-сопряженный ток.
Полная комплексная мощность трехфазной нагрузки в 3 раза больше:
$$ \tilde{S} = 3 \cdot \tilde{S}_Ф = 3 U_Ф I_Ф (\cos\phi + j\sin\phi) = P + jQ $$
Отсюда, полная активная мощность \( P = 3 P_Ф = 3 U_Ф I_Ф \cos\phi \), а полная реактивная мощность \( Q = 3 Q_Ф = 3 U_Ф I_Ф \sin\phi \).
Эти выражения можно выразить через линейные токи и напряжения. Как для схемы «звезда», так и для схемы «треугольник» (при симметрии), преобразование приводит к универсальным формулам:
- Активная мощность: \( P = \sqrt{3} \cdot U_Л I_Л \cos\phi \)
- Реактивная мощность: \( Q = \sqrt{3} \cdot U_Л I_Л \sin\phi \)
- Полная (кажущаяся) мощность: \( S = \sqrt{P^2 + Q^2} = \sqrt{3} \cdot U_Л I_Л \)
Важное замечание: В формулах мощности через линейные величины \( (P = \sqrt{3} \cdot U_Л I_Л \cos\phi) \), угол \( \phi \) — это по-прежнему сдвиг по фазе между фазным напряжением и фазным током, а не между линейными.
Заметим, что мгновенная мощность всей симметричной трехфазной цепи постоянна и равна ее активной мощности, что является одним из главных преимуществ таких систем.
5. Несимметричные режимы в трехфазных цепях
Нарушение симметрии (несимметричный режим) возникает, когда комплексные сопротивления фаз нагрузки не равны друг другу: \( Z_a \neq Z_b \neq Z_c \). Расчет таких цепей усложняется, и их нельзя сводить к одной эквивалентной фазе.
5.1. Схема «Звезда — звезда» с нейтральным проводом
Из-за наличия нейтрального провода (считаем его сопротивление равным нулю) напряжение на каждой фазе нагрузки остается неизменным и равным фазному напряжению генератора (\( \dot{U}_{a0′} = \dot{U}_{A0} \)). Каждая фаза оказывается автономна. Токи в фазах будут различными и определяются по закону Ома для каждой фазы:
$$ \dot{I}_a = \frac{\dot{U}_{A0}}{Z_a}, \quad \dot{I}_b = \frac{\dot{U}_{B0}}{Z_b}, \quad \dot{I}_c = \frac{\dot{U}_{C0}}{Z_c} $$
Сумма этих токов не равна нулю, и в нейтральном проводе появляется ток \( \dot{I}_0 = \dot{I}_a + \dot{I}_b + \dot{I}_c \neq 0 \).
Большим преимуществом этой схемы является то, что напряжения на фазах нагрузки остаются неизменными и не зависящими от сопротивления нагрузки. Это защищает потребителей от перепадов напряжения.
5.2. Схема «Звезда — звезда» без нейтрального провода
Это самый опасный режим при несимметричной нагрузке. При обрыве или отсутствии нейтрали потенциалы точек 0 и 0′ перестают быть равными. Расчет ведется, например, методом двух узлов. Напряжение между нейтральными точками (напряжение смещения нейтрали) определяется как:
$$ \dot{U}_{O’O} = \frac{ \frac{\dot{E}_A}{Z_a} + \frac{\dot{E}_B}{Z_b} + \frac{\dot{E}_C}{Z_c} }{ \frac{1}{Z_a} + \frac{1}{Z_b} + \frac{1}{Z_c} } $$
(Здесь \( Z_a, Z_b, Z_c \) — полные сопротивления фаз, включая линию).
При этом напряжение на фазах нагрузки оказывается различным и не равным номинальному:
$$ \dot{U}_{aO’} = \dot{E}_A — \dot{U}_{O’O}, \quad \dot{U}_{bO’} = \dot{E}_B — \dot{U}_{O’O}, \quad \dot{U}_{cO’} = \dot{E}_C — \dot{U}_{O’O} $$
В одних фазах напряжение может быть пониженным, а в других — повышенным, что может привести к выходу из строя электроприборов.
5.3. Схема «Треугольник»
При несимметричной нагрузке в схеме «треугольник» напряжения на фазах нагрузки остаются неизменными и равными линейным напряжениям. Токи в фазах будут различными:
$$ \dot{I}_{ab} = \frac{\dot{U}_{ab}}{Z_{ab}}, \quad \dot{I}_{bc} = \frac{\dot{U}_{bc}}{Z_{bc}}, \quad \dot{I}_{ca} = \frac{\dot{U}_{ca}}{Z_{ca}} $$
Линейные токи также будут несимметричны и определяются по закону Кирхгофа:
$$ \dot{I}_a = \dot{I}_{ab} — \dot{I}_{ca} $$
Этот режим не так опасен для нагрузки, как Y-Y без нейтрали, так как перекоса фазных напряжений не происходит.
6. Измерение мощности в трехфазных цепях
Для измерения активной мощности трехфазной нагрузки в общем случае (4-проводная несимметричная цепь) используют схему трех ваттметров (рис. 7а). Каждый ваттметр измеряет мощность своей фазы, и полная мощность равна сумме их показаний:
$$ P = P_{W1} + P_{W2} + P_{W3} $$
При симметричной нагрузке достаточно одного ваттметра, включенного в одну из фаз; его показания нужно умножить на 3.
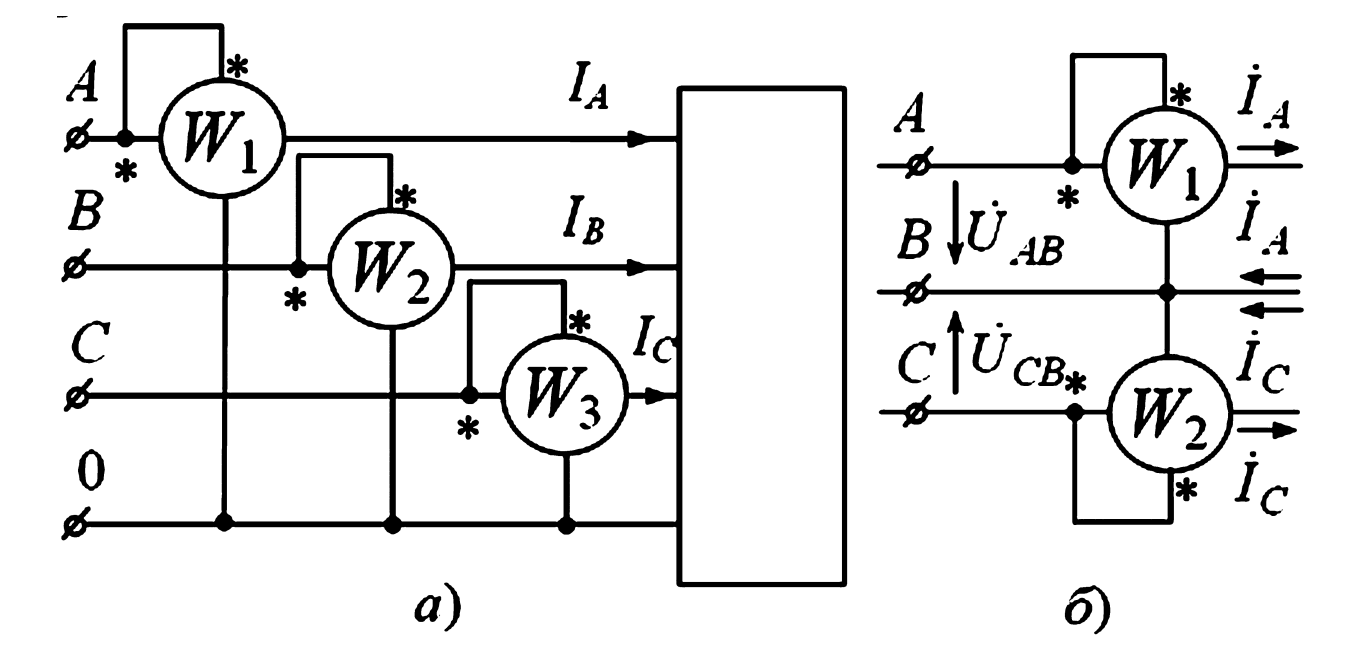
Рис. 7. Схема измерения мощности в трехфазной цепи: а — с помощью трех ваттметров; б — с помощью двух ваттметров.
В трехпроводной цепи (без нейтрали) активную мощность можно измерить с помощью схемы двух ваттметров (схема Арона), независимо от симметрии нагрузки (рис. 7б). Это следует из теоремы Блонделя, которая гласит, что для измерения мощности в N-проводной системе достаточно N-1 ваттметра.
Трехпроводную цепь всегда можно рассматривать как две двухпроводные линии, имеющие один общий провод (например, B). Ваттметр 1 (W1) измеряет мощность \( P_1 \), используя ток \( \dot{I}_A \) и напряжение \( \dot{U}_{AB} \). Ваттметр 2 (W2) измеряет \( P_2 \), используя ток \( \dot{I}_C \) и напряжение \( \dot{U}_{CB} \).
Полное значение передаваемой активной мощности равно алгебраической сумме показаний обоих ваттметров:
$$ P = P_{W1} + P_{W2} $$
При некоторых углах сдвига фаз (когда \( \cos\phi < 0.5 \)) один из ваттметров может показывать отрицательное значение; в этом случае его показания вычитаются. При чисто активной нагрузке (\( \phi = 0 \)) показания обоих ваттметров одинаковы.
Интересные факты о трехфазных системах
- Постоянная мощность: Суммарная мгновенная мощность в симметричной трехфазной системе постоянна и не пульсирует, как в однофазной. Это обеспечивает плавный крутящий момент в двигателях.
- Вращающееся магнитное поле: Именно пространственный сдвиг обмоток статора на 120° и временной сдвиг токов на 120° создают вращающееся магнитное поле — основу работы асинхронных двигателей.
- Направление вращения: Чтобы изменить направление вращения (реверсировать) трехфазного двигателя, достаточно поменять местами любые два из трех линейных проводов.
- Спор об изобретении: Хотя Никола Тесла широко известен своими патентами на многофазные системы (в основном двухфазные), именно Михаил Доливо-Добровольский создал первую работоспособную и экономически эффективную трехфазную систему.
- Режим «открытого треугольника»: Если в группе из трех однофазных трансформаторов, соединенных треугольником, один выйдет из строя, система может продолжать работать (с двумя трансформаторами), выдавая около 58% от первоначальной мощности.
- Экономия на материалах: Для передачи одинаковой мощности на одинаковое расстояние трехфазная система требует примерно на 25% меньше меди для проводов, чем однофазная система.
- Число \( \sqrt{3} \): Коэффициент \( \sqrt{3} \approx 1.732 \) является «магическим числом» в трехфазных цепях, связывая линейные и фазные величины в звезде и треугольнике.
FAQ: Часто задаваемые вопросы
Трехфазная система представляет собой оптимальный компромисс между экономичностью (меньший расход меди по сравнению с 1- и 2-фазными системами) и сложностью конструкции. При увеличении числа фаз (4, 6, 12) дальнейшая экономия на проводах становится незначительной, а конструкция генераторов, трансформаторов и двигателей резко усложняется.
Это напряжения в четырехпроводной сети, соединенной «звездой». 220 В (или 230 В по ГОСТ 29322-2014) — это фазное напряжение (между любым линейным проводом A, B, или C и нейтральным проводом N). 380 В (или 400 В) — это линейное напряжение (между двумя линейными проводами, A-B, B-C или C-A). Они связаны соотношением: \( 220 \text{ В} \cdot \sqrt{3} \approx 380 \text{ В} \).
Это аварийная ситуация в схеме «звезда-звезда» с нейтральным проводом (самая частая в жилых домах). Если нейтральный провод обрывается, а нагрузка на фазах несимметрична (что почти всегда так: в одной комнате включен чайник, в другой — только лампочка), происходит «перекос фаз». Напряжение на фазах с малой нагрузкой резко возрастает (до 380 В), а на фазах с большой нагрузкой — падает. Это приводит к массовому выходу из строя бытовой техники.
Да, это возможно, но не напрямую. Требуется создать «искусственную» третью фазу. Чаще всего это делают с помощью фазосдвигающего конденсатора (потеря мощности до 40%) или, что более современно и эффективно, с помощью частотного преобразователя (ЧПУ или VFD), который преобразует однофазное напряжение в полноценное трехфазное с возможностью регулировки оборотов.
Это коэффициент мощности. Он показывает, какая доля полной мощности (S), потребляемой из сети, превращается в полезную (активную) работу (P). Он равен косинусу угла \( \phi \) между фазным напряжением и фазным током. Если \( \cos\phi = 1 \) (идеально для активной нагрузки типа ТЭНа), то вся мощность идет в работу. Если \( \cos\phi = 0 \) (идеально для конденсатора или катушки), работа не совершается. У асинхронных двигателей \( \cos\phi \) обычно 0.8-0.9.
Он равен их векторной сумме (разности). Фазные токи \( \dot{I}_{ab} \) и \( \dot{I}_{ca} \), втекающие в узел A, сдвинуты по фазе друг относительно друга (на 120° при симметричной нагрузке). Сложение двух векторов, сдвинутых на 120°, дает результирующий вектор, который в \( \sqrt{3} \) раз больше каждого из них (при их равенстве).
Это следует из теоремы Блонделя. В 3-проводной системе ток в одном из проводов (например, B) всегда равен сумме токов в двух других с обратным знаком: \( \dot{I}_B = -(\dot{I}_A + \dot{I}_C) \). Так как один из токов линейно зависим, для полного описания мощности системы достаточно знать параметры только двух независимых линий (A и C), используя третий (B) как общий обратный провод.
Заключение
Трехфазные системы являются фундаментальной основой современной электроэнергетики. Их доминирование обусловлено высокой экономической эффективностью передачи энергии и превосходными эксплуатационными характеристиками трехфазных электрических машин.
Понимание двух основных схем соединения — «звезда» (Y) и «треугольник» (Δ) — и соотношений между фазными и линейными величинами (\( \sqrt{3} \)) является ключевым для расчета и анализа таких цепей. В то время как симметричные режимы позволяют использовать простой метод однофазного эквивалента, анализ несимметричных режимов требует более сложных подходов и выявляет потенциальные опасности, такие как смещение нейтрали.
Нормативная база
- ГОСТ 29322-2014 (IEC 60038:2009) «Напряжения стандартные» — Устанавливает стандартные номинальные напряжения для систем электроснабжения, включая 230/400 В.
- ГОСТ 32144-2013 «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения» — Регламентирует показатели качества электроэнергии, в том числе отклонения напряжения.
- ПУЭ (Правила устройства электроустановок) — Основной свод правил, регламентирующий проектирование, монтаж и эксплуатацию электроустановок в РФ, включая требования к трехфазным сетям.
Список рекомендуемой литературы
- Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Высшая школа, 2007.
- Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов. — М.: Энергоатомиздат, 2005.
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. — М.: Энергоатомиздат, 1989.