Расчет тепловых режимов электрических аппаратов: теория, примеры

Содержание страницы

1. Источники теплоты: Физика возникновения потерь
2. Задачи тепловых расчетов и Механизмы теплопередачи
3. Конструктивные методы улучшения охлаждения
4. Динамика нагрева: Переходные процессы
5. Режимы работы электрических аппаратов
6. Термическая стойкость при коротких замыканиях (КЗ)
7. Практический пример: Комплексный тепловой расчет шинопровода
8. Сравнительный анализ эффективности систем охлаждения и материалов
9. Интересные факты о тепловых процессах
10. FAQ: Часто задаваемые вопросы
Заключение

Тепловые процессы в электрических аппаратах — это совокупность физических явлений, связанных с выделением, распространением и отводом тепловой энергии, возникающей при работе электротехнического устройства.

Исторически проблема нагрева встала перед инженерами одновременно с появлением первых мощных генераторов в XIX веке. Закон Джоуля-Ленца (1841 г.) стал отправной точкой, однако с ростом мощностей выяснилось, что простой формулы \( I^2R \) недостаточно. Инженеры столкнулись с тем, что массивные проводники плавились при токах, которые теоретически должны были выдерживать, а изоляция разрушалась из-за неочевидных тепловых полей.

В современной электроэнергетике тепловой расчет — это ключевой этап проектирования. От него зависит класс изоляции, габариты устройства, выбор материалов контактов и, в конечном счете, пожарная безопасность объекта. Неверный расчет приводит к ускоренному старению изоляции (правило 8 градусов: повышение температуры на 8°C сокращает срок службы изоляции вдвое) или к аварийным взрывам при коротких замыканиях.

1. Источники теплоты: Физика возникновения потерь

Любой электрический аппарат с точки зрения термодинамики является телом с внутренними источниками тепловыделения. Эти источники делятся на основные (в токоведущих частях) и дополнительные (в конструктивных элементах). Рассмотрим их детально.

1.1. Активная мощность и зависимость сопротивления от температуры

Базовым источником тепла является протекание тока по проводнику. На постоянном токе мощность потерь определяется омическим сопротивлением: \( P = I^2 R \). Однако важно понимать, что само сопротивление \( R \) не является константой. С ростом температуры кристаллическая решетка металла начинает колебаться интенсивнее, чаще сталкиваясь с носителями заряда (электронами), что увеличивает сопротивление.

Зависимость сопротивления от температуры описывается формулой: \[ R_t = R_{20} [1 + \alpha (\vartheta — 20)] \] где: \( R_{20} \) — сопротивление при 20°C; \( \alpha \) — температурный коэффициент сопротивления (для меди и алюминия \(\approx 0.004 \, 1/^\circ C\)); \( \vartheta \) — текущая температура проводника.

Это создает положительную обратную связь: ток греет проводник -> сопротивление растет -> выделяемая мощность растет (при источнике тока) -> проводник греется еще сильнее.

1.2. Особенности переменного тока: Скин-эффект и Эффект близости

На переменном токе ситуация усложняется. Активное сопротивление \( R_{\approx} \) всегда больше омического \( R_{=} \). Это вызвано явлениями электромагнитной индукции внутри самого проводника.

Поверхностный эффект (Скин-эффект)

Переменный магнитный поток, пронизывающий проводник, индуцирует в нем вихревые токи. В центре сечения проводника эти токи направлены против основного тока, а на периферии — совпадают с ним. В результате плотность тока в центре снижается практически до нуля, а основная масса электронов перемещается в тонкий поверхностный слой (скин-слой).

Аналогия: толпа людей в коридоре
Представьте широкий коридор, по которому движется толпа людей.
Спокойное, однонаправленное движение (постоянный ток):
Люди равномерно используют всю ширину коридора. Никто никому не мешает, и пропускная способность максимальна.
Частая смена направления движения (переменный ток высокой частоты):
Поток людей начинает постоянно разворачиваться вперёд-назад.
В центре коридора встречные потоки чаще сталкиваются, мешают друг другу и резко замедляются — движение там становится неэффективным.
У стен коридора ситуация иная:
С одной стороны нет встречного потока, поэтому люди могут двигаться быстрее и согласованнее.
В итоге большая часть людей инстинктивно смещается к стенам, а центр коридора остаётся почти пустым.

Это явление учитывается коэффициентом \( K_П \). Для массивных шин на частоте 50 Гц он может достигать значений 1.1–1.2, а на высоких частотах — десятков единиц.

Эффект близости

Этот эффект возникает в системе из нескольких проводников (например, трехфазная система шин). Магнитное поле одного проводника наводит вихревые токи в соседнем. Это приводит к перераспределению плотности тока по сечению: ток «прижимается» к той стороне шины, которая ближе (или дальше, в зависимости от направления токов) к соседу. Коэффициент близости \( K_Б \) может значительно увеличить потери в крайних фазах шинопроводов.
Суммарная мощность потерь на переменном токе:
\[ P_{\approx} = K_П K_Б I^2 R_{=} \]
Пренебрежение коэффициентами \( K_П \) и \( K_Б \) при проектировании мощных токопроводов (на токи свыше 1000 А) недопустимо и ведет к перегреву.

1.3. Потери в нетоковедущих частях и изоляции

Помимо проводников, греются и другие элементы:

Ферромагнитные детали (сталь): Корпуса, скобы, магнитопроводы греются из-за вихревых токов и гистерезиса (перемагничивания).
Изоляция: Диэлектрические потери возникают из-за периодической поляризации диэлектрика. Для аппаратов высокого напряжения это значимый фактор.
Электрическая дуга: Специфический источник тепла в коммутационных аппаратах. Температура столба дуги достигает 6000–12000 К, что требует мгновенного отвода тепла и гашения.

2. Задачи тепловых расчетов и Механизмы теплопередачи

Инженерная задача сводится к поиску баланса: мощность, выделяемая внутри, должна быть успешно отдана наружу, при этом температура самой горячей точки не должна превысить лимит для выбранного класса изоляции.

Существует два класса задач теплового расчета:

Прямая задача (Поверочный расчет): Известна конструкция, размеры и ток. Нужно найти температуру. Если она ниже допустимой — аппарат годен.
Обратная задача (Проектировочный расчет): Известна допустимая температура и ток. Нужно найти минимально необходимые размеры поверхности охлаждения \( S_{охл} \). Это более сложная задача, решаемая часто методом последовательных приближений.

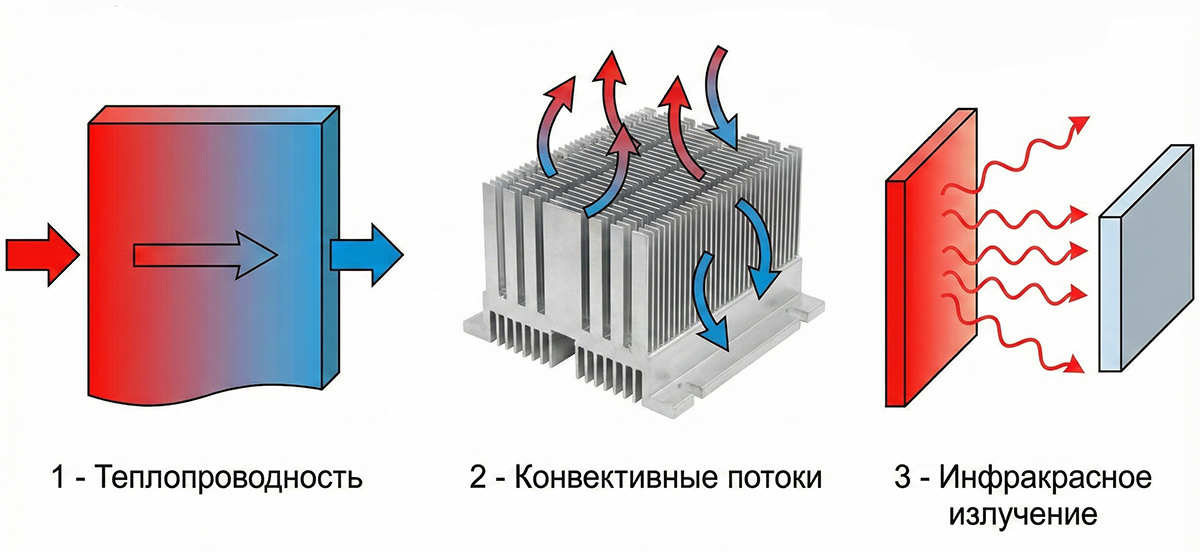
схематично изображены три вида теплопередачи: 1 - Теплопроводность через стенку металла, 2 - Конвективные потоки воздуха, обтекающие радиатор, 3 - Инфракрасное излучение от нагретой поверхности

Рисунок 1 – Основные способы распространения теплоты в электрических аппаратах.

2.1. Теплопроводность

Передача энергии от более нагретых частей тела к менее нагретым при непосредственном контакте. В металлах за это отвечают свободные электроны. Этот механизм критически важен для отвода тепла от внутренних слоев многовитковой катушки к ее поверхности. Плохая теплопроводность воздуха внутри катушки (пустоты) может создать «тепловой мешок» и пробой изоляции, поэтому катушки часто пропитывают компаундами (вакуумная пропитка).

2.2. Конвекция

Унос тепла движущимися массами газа (воздуха) или жидкости (масла).

Естественная конвекция: Нагретый воздух становится легче и поднимается вверх. Эффективность зависит от расположения поверхностей (вертикальные ребра охлаждаются лучше горизонтальных).
Принудительная конвекция: Использование вентиляторов или насосов. Позволяет уменьшить габариты аппарата в разы при той же мощности.

2.3. Тепловое излучение

Передача энергии электромагнитными волнами. Любое нагретое тело излучает инфракрасные лучи. Мощность излучения зависит от состояния поверхности. Черное матовое тело излучает намного эффективнее, чем полированное блестящее.

Именно поэтому радиаторы силовой электроники часто анодируют в черный цвет. Это повышает коэффициент теплоотдачи излучением.

2.4. Тепловой закон Ома

Для упрощения стационарных расчетов (когда температура не меняется во времени) сложный процесс конвекции и излучения объединяют в один коэффициент теплоотдачи \( k_{ТО} \). Уравнение Ньютона-Рихмана записывается так:

P = k_{ТО} S_{охл} (\vartheta_А — \vartheta_О) \] Или в виде, аналогичном закону Ома: \[ \Delta \vartheta = \frac{P}{k_{ТО} S_{охл}}

Здесь \( \frac{1}{k_{ТО} S_{охл}} \) играет роль теплового сопротивления. Чтобы уменьшить нагрев \( \Delta \vartheta \), нужно либо снижать потери \( P \), либо уменьшать тепловое сопротивление (увеличивать площадь \( S_{охл} \) или интенсивность обдува \( k_{ТО} \)).

3. Конструктивные методы улучшения охлаждения

Как инженер может повлиять на тепловой режим?

Выбор материала: Медь имеет меньшее удельное сопротивление, чем алюминий, а значит, выделяет меньше тепла при том же токе.
Форма проводников: Трубчатые или коробчатые шины имеют большую поверхность охлаждения при том же сечении и меньший коэффициент поверхностного эффекта.
Радиаторы: Искусственное увеличение поверхности \( S_{охл} \) путем оребрения.
Окраска: Применение красок с высоким коэффициентом излучения (неметаллические эмали).
Шихтовка магнитопроводов: Для снижения вихревых токов в «железе» его набирают из тонких изолированных листов электротехнической стали.

Таблица 1 – Сравнение эффективности материалов и конструкций
Параметр	Медная шина (прямоугольная)	Алюминиевая шина (трубчатая)	Влияние на нагрев
Удельное сопротивление	Низкое (0.017 мкОм·м)	Среднее (0.028 мкОм·м)	Медь греется меньше при прочих равных.
Скин-эффект	Заметен в толстых шинах	Минимален (нет сердцевины)	Труба эффективнее использует материал.
Теплоотдача	Средняя (зависит от периметра)	Высокая (обдув снаружи и изнутри)	Трубчатая конструкция лучше охлаждается.

4. Динамика нагрева: Переходные процессы

Аппарат никогда не нагревается мгновенно. Из-за наличия теплоемкости материала \( C \) (аналог электрической емкости) процесс растянут во времени.

4.1. Уравнение теплового баланса

Рассмотрим включение холодного аппарата под нагрузку. В каждый бесконечно малый момент времени \( dt \) выделяемая энергия распределяется на две части:

\[ P dt = C d\vartheta + k_{ТО} S_{охл} \vartheta dt \] Где: \( P dt \) — пришедшая энергия (Джоулево тепло); \( C d\vartheta \) — энергия, поглощенная телом (идет на рост температуры); \( k_{ТО} S_{охл} \vartheta dt \) — энергия, рассеянная в среду.

В начальный момент (\( t=0, \vartheta=0 \)) вся энергия идет на нагрев (теплоотдачи нет, так как нет разницы температур). В конце процесса (\( t=\infty \)) вся энергия уходит в среду, температура перестает расти.

4.2. Экспонента нагрева и постоянная времени

Решением дифференциального уравнения является экспонента:
\[ \vartheta(t) = \vartheta_{У} (1 — e^{-t/T}) \]
Ключевой параметр здесь — Постоянная времени нагрева \( T \):
\[ T = \frac{C}{k_{ТО} S_{охл}} \]
Физический смысл \( T \): это время, за которое аппарат достиг бы установившейся температуры \( \vartheta_{У} \), если бы теплоотдача полностью отсутствовала (адиабатный нагрев).
В реальности за время \( t = T \) аппарат нагревается до 63% от максимума. За \( t = 3T \) — до 95%. Полным установлением режима считается время \( 4T \dots 5T \).

Рисунок 2 – Кривые нагрева (1) и охлаждения (2) электрического аппарата.
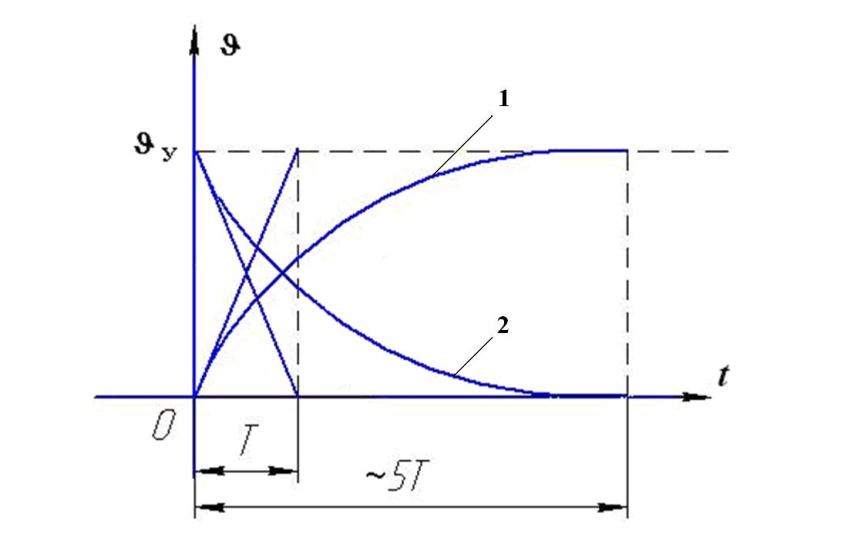
Описания:
1 – процесс нарастания температуры при включении под нагрузку;
2 – процесс спада температуры после отключения источника тепла.

При отключении питания происходит обратный процесс — охлаждение:
\[ \vartheta(t) = \vartheta_{У} e^{-t/T} \]
Важно отметить, что постоянная времени охлаждения может отличаться от постоянной нагрева, если меняются условия охлаждения (например, самовентилируемый двигатель останавливается, и обдув прекращается).

5. Режимы работы электрических аппаратов

Выбор аппарата зависит не только от величины тока, но и от того, как долго этот ток протекает. ГОСТ выделяет несколько режимов:

Продолжительный (S1): Время работы \( t_p > 4T \). Температура успевает достигнуть максимума \( \vartheta_{У} \). Все номинальные параметры указываются для этого режима.
Кратковременный (S2): Время работы мало (\( t_p < 4T \)), аппарат не успевает нагреться до максимума, но затем следует долгая пауза, за которую он полностью остывает. В этом режиме аппарат можно перегружать током выше номинального, так как перегрев не будет достигнут.
Повторно-кратковременный (S3): Режим циклов «Работа — Пауза». Характеризуется параметром ПВ (Продолжительность Включения).

ПВ\% = \frac{t_p}{t_p + t_П} \cdot 100\%

Стандартные значения ПВ: 15%, 25%, 40%, 60%.
В этом режиме допустима перегрузка по току. Коэффициент перегрузки \( k_I \) показывает, во сколько раз ток может быть больше номинального тока продолжительного режима:
\[ k_I = \sqrt{\frac{100}{ПВ\%}} \]
Например, при ПВ=25% ток можно увеличить в \( \sqrt{4} = 2 \) раза.

6. Термическая стойкость при коротких замыканиях (КЗ)

Режим КЗ — самый опасный аварийный режим. Токи могут возрастать в десятки раз. Тепловые процессы здесь протекают иначе.

6.1. Адиабатный процесс

Так как КЗ длится очень мало (доли секунд), тепло не успевает уйти от проводника в изоляцию или воздух. Считается, что все выделенное тепло идет только на повышение температуры металла. Этот процесс называется адиабатным.

Критерием выживания аппарата является Термическая стойкость — способность выдержать тепловой удар без разрушения.
Предельные температуры при КЗ (кратковременно!):

Медные шины: до 300°C (при длительной норме 70–90°C).
Алюминиевые шины: до 200°C.

Важно: Превышение этих температур ведет к необратимому отжигу меди (потере механической прочности), плавлению алюминия и взрывообразному разрушению изоляции.

Рисунок 3 – Адиабатные кривые нагрева проводников. Видно, что при одинаковом воздействии сталь нагревается быстрее алюминия, а алюминий быстрее меди из-за разной теплоемкости и сопротивления.

6.2. Интеграл Джоуля и расчет

Мерой теплового воздействия тока КЗ является Интеграл Джоуля \( B_k \) — суммарная энергия, прошедшая через цепь:

B_k = \int_{0}^{t_{откл}} i^2 dt

Он учитывает и периодическую (синусоидальную), и апериодическую (затухающую) составляющие тока КЗ.
Условие термической стойкости аппарата:
\[ B_k \le I^2_{тер} \cdot t_{тер} \]
где \( I_{тер} \) и \( t_{тер} \) — паспортные данные аппарата (ток и время термической стойкости).

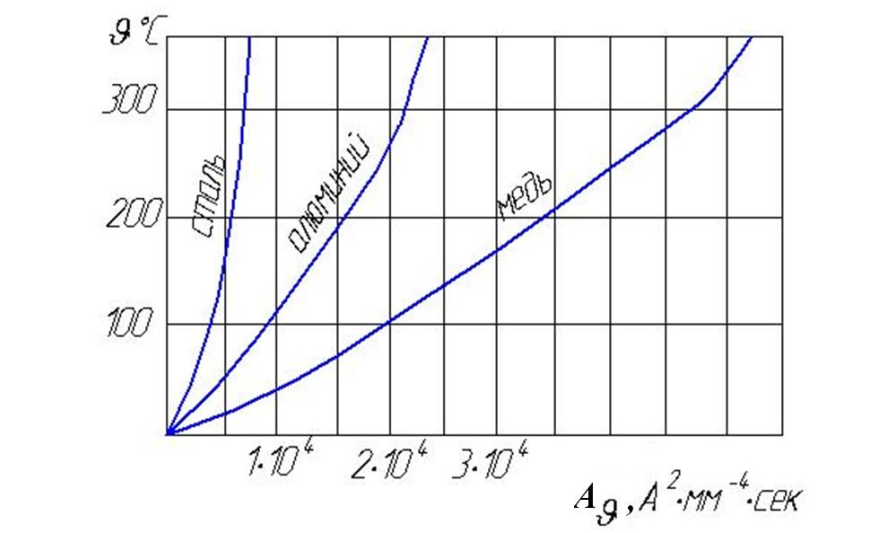
6.3. Графический метод определения температуры

Для практических расчетов используют диаграммы с вспомогательной функцией \( A(\vartheta) \).

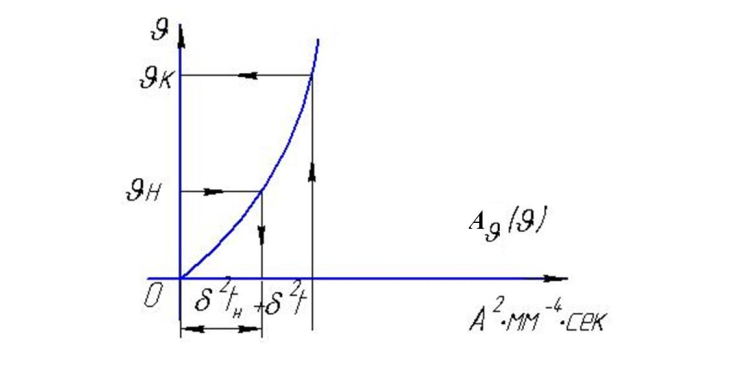
Рисунок 4 – Пример определения конечной температуры проводника при КЗ.
а – определение начального параметра \( A_{\vartheta_H} \);
б – добавление величины нагрева (пропорциональной интегралу Джоуля);
в – нахождение конечной температуры \( \vartheta_K \).

Алгоритм:

1. По начальной температуре \( \vartheta_H \) находим по кривой значение \( A_{\vartheta_H} \).
2. Вычисляем добавку: \( \Delta A = \frac{B_k}{S^2} \) (где \( S \) — сечение).
3. Находим конечное значение \( A_K = A_H + \Delta A \).
4. По графику возвращаемся к температуре и находим \( \vartheta_K \).
5. Сравниваем \( \vartheta_K \) с допустимой по ГОСТ 30323-95.

7. Практический пример: Комплексный тепловой расчет шинопровода

Рассмотрим реальную инженерную задачу. Нам необходимо проверить тепловой режим медной шины распределительного устройства 0.4 кВ и убедиться в её стойкости к токам короткого замыкания (КЗ).

Исходные данные:

Материал: Медь твердая (М1Т).
Сечение шины: \( 100 \times 10 \) мм (одиночная полоса).
Рабочий ток (S1): \( I_{раб} = 2000 \) А.
Ток короткого замыкания: \( I_{к} = 40 \) кА (действующее значение).
Время отключения КЗ: \( t_{откл} = 0.5 \) с.
Температура среды: \( \vartheta_{0} = 25^\circ C \).
Допустимая температура (ГОСТ): \( [\vartheta]_{дл} = 90^\circ C \) (длительная), \( [\vartheta]_{кз} = 300^\circ C \) (при КЗ).

Этап 1: Геометрические и электрические параметры

Сначала определим активное сопротивление шины длиной 1 метр.

1. Площадь поперечного сечения \( S \) и периметр охлаждения \( P_{охл} \):

S = 100 \cdot 10 = 1000 \, \text{мм}^2 = 10^{-3} \, \text{м}^2 \] \[ P_{охл} = 2 \cdot (0.1 + 0.01) = 0.22 \, \text{м}^2/\text{м} \quad (\text{периметр на 1 метр длины})

2. Сопротивление постоянному току при 20°C (\( \rho_{20} = 0.0175 \, \text{Ом} \cdot \text{мм}^2/\text{м} \)):

R_{20} = \frac{\rho_{20}}{S} = \frac{0.0175}{1000} = 17.5 \cdot 10^{-6} \, \text{Ом/м}

Этап 2: Учет нагрева и скин-эффекта

Тепловой расчет — процесс итерационный. Мы должны предположить температуру шины, найти сопротивление при этой температуре, вычислить потери, а затем проверить, нагреется ли шина до предполагаемой температуры.

Предположим, что шина нагреется до \( \vartheta = 85^\circ C \).

1. Сопротивление постоянному току при 85°C:

R_{85} = R_{20} [1 + \alpha (\vartheta — 20)] = 17.5 \cdot 10^{-6} [1 + 0.004 (85 — 20)] \] \[ R_{85} = 17.5 \cdot 10^{-6} \cdot 1.26 = 22.05 \cdot 10^{-6} \, \text{Ом/м}

Как видим, нагрев увеличил сопротивление на 26%.

2. Сопротивление переменному току (50 Гц). Для шин сечением \( 100 \times 10 \) мм коэффициент поверхностного эффекта \( K_{П} \approx 1.02 \) (скин-эффект невелик), а коэффициент близости (для средней фазы при расстоянии между фазами 100 мм) \( K_{Б} \approx 1.1 \).

R_{\approx} = R_{85} \cdot K_{П} \cdot K_{Б} = 22.05 \cdot 1.02 \cdot 1.1 \approx 24.7 \cdot 10^{-6} \, \text{Ом/м}

Этап 3: Расчет установившейся температуры

1. Мощность тепловых потерь на 1 метр длины:

P = I^2 \cdot R_{\approx} = 2000^2 \cdot 24.7 \cdot 10^{-6} = 4 \cdot 10^6 \cdot 24.7 \cdot 10^{-6} = 98.8 \, \text{Вт/м}

Каждый метр шины работает как нагреватель мощностью почти 100 Вт.

2. Определим температуру перегрева.
Применим упрощенный коэффициент теплоотдачи для окрашенной шины в спокойном воздухе: \( k_{ТО} \approx 12 \, \text{Вт}/(\text{м}^2 \cdot ^\circ \text{C}) \).
Используем «Тепловой закон Ома» (2):

\Delta \vartheta = \frac{P}{k_{ТО} \cdot S_{охл}} = \frac{98.8}{12 \cdot 0.22} = \frac{98.8}{2.64} \approx 37.4^\circ C

3. Итоговая температура шины:
\[ \vartheta_{рез} = \vartheta_{0} + \Delta \vartheta = 25 + 37.4 = 62.4^\circ C \]

Вывод по режиму S1: Расчетная температура \( 62.4^\circ C \) значительно ниже допустимых \( 90^\circ C \).

Почему мы получили меньше 85°C? Потому что сечение выбрано с запасом. Инженер может принять решение уменьшить сечение (для экономии меди) или оставить запас на случай ухудшения вентиляции.

Этап 4: Проверка на термическую стойкость (КЗ)

Теперь представим, что произошла авария. Ток \( I_k = 40 \) кА течет 0.5 секунды. Проверим, не расплавится ли наша шина.
Воспользуемся критерием термической стойкости через плотность тока, упрощая метод интеграла Джоуля.

1. Минимальное сечение проводника по термической стойкости определяется формулой:

S_{min} = \frac{I_k \cdot \sqrt{t_{откл}}}{C_{тер}}

Где \( C_{тер} \) — термический коэффициент материала (функция от допустимой температуры). Для меди (при нагреве от длительной до предельной температуры 300°C) \( C_{тер} \approx 170 \).

S_{min} = \frac{40000 \cdot \sqrt{0.5}}{170} = \frac{40000 \cdot 0.707}{170} = \frac{28280}{170} \approx 166 \, \text{мм}^2

2. Сравнение:
Наше фактическое сечение \( S_{факт} = 1000 \, \text{мм}^2 \).
Требуемое минимальное сечение \( S_{min} = 166 \, \text{мм}^2 \).

Аналогия:
Представьте, что ток КЗ — это мощный поток воды (цунами), а сечение провода — это ширина русла реки. Нам нужно русло шириной минимум 166 метров, чтобы вода не вышла из берегов (не перегрела провод). У нас есть русло шириной 1000 метров.

Итоговое заключение инженера:
Шина \( 100 \times 10 \) мм выбрана с большим запасом.1. В рабочем режиме она нагреется всего до \( \approx 62^\circ C \) (норма).2. При коротком замыкании она нагреется незначительно (всего на 5-10 градусов), так как её масса велика для такого импульса энергии.
Конструкция надежна.

8. Сравнительный анализ эффективности систем охлаждения и материалов

Выбор способа охлаждения и материала токоведущих частей — это всегда поиск экономического оптимума. Увеличение интенсивности охлаждения позволяет уменьшить габариты аппарата (сэкономить медь и сталь), но усложняет конструкцию (добавляет вентиляторы, насосы, радиаторы) и снижает общую надежность системы.

8.1. Сравнение методов охлаждения

В таблице ниже приведены эмпирические данные по эффективности различных сред. Ключевым параметром является коэффициент теплоотдачи \( k_{TO} \), показывающий, сколько ватт тепла уходит с одного квадратного метра поверхности при разнице температур в 1 градус.

Таблица 2. Сравнительная характеристика способов охлаждения в электрических аппаратах
Способ охлаждения	Коэфф. теплоотдачи \( k_{TO} \), \( \frac{Вт}{м^2 \cdot K} \)	Преимущества	Недостатки	Типовое применение
Естественное воздушное (Конвекция + Излучение)	5 … 15	Максимальная надежность (нет движущихся частей). Бесшумность. Нулевые эксплуатационные расходы.	Низкая эффективность. Требует больших габаритов аппарата. Сильная зависимость от положения в пространстве.	Распределительные щиты, разъединители, сухие трансформаторы малой мощности.
Принудительное воздушное (Вентиляторы)	20 … 50	Уменьшение массы аппарата на 30-40%. Возможность управления потоком (вкл/выкл).	Шум. Засасывание пыли внутрь. Риск перегрева при отказе вентилятора.	Силовые шкафы, частотные преобразователи, тяговые двигатели.
Масляное естественное (ONAN)	50 … 150	Высокая теплоемкость носителя. Масло является отличным диэлектриком (защита изоляции).	Пожароопасность. Необходимость герметичного бака. Экологические риски протечек.	Силовые трансформаторы, масляные выключатели.
Водяное охлаждение (Непосредственное или через теплообменник)	500 … 2500+	Колоссальная эффективность. Минимальные габариты устройства.	Сложность (насосы, фильтры, деионизация воды). Риск коррозии и электролиза. Высокая стоимость обслуживания.	Генераторы ГЭС/ТЭС, тиристорные блоки, индукционные печи.

Примечание: Переход от естественного воздушного охлаждения к водяному позволяет увеличить плотность тока в проводнике с \( 2..3 \, А/мм^2 \) до \( 15..20 \, А/мм^2 \). Однако стоимость системы охлаждения при этом возрастает на порядок.

8.2. Сравнение материалов токоведущих частей

Правильный выбор материала — это баланс между проводимостью (снижение источника тепла) и теплоемкостью (способностью поглотить тепловой удар при КЗ).

Таблица 3. Теплофизические параметры проводниковых материалов
Параметр	Медь (M1)	Алюминий (АД31)	Сталь (Ст3)	Латунь (Л63)
Удельное сопротивление \( \rho_{20} \), \( \frac{Ом \cdot мм^2}{м} \) (Чем меньше, тем меньше тепла выделяется)	0.0172	0.028	0.10 … 0.15	0.07
Теплопроводность \( \lambda \), \( \frac{Вт}{м \cdot K} \) (Способность выводить тепло из зоны нагрева)	390	220	50	110
Удельная теплоемкость \( c \), \( \frac{Дж}{кг \cdot K} \) (Тепловая инерция)	385	900	460	380
Температура плавления, °C	1083	660	~1500	906
Коэфф. линейного расширения, \( 10^{-6} K^{-1} \) (Риск механического разрушения при нагреве)	16.7	23.8	12.0	18.5

Обратите внимание: Хотя у алюминия удельная теплоемкость выше, чем у меди (900 против 385), его плотность в 3.3 раза меньше. Поэтому объемная теплоемкость (способность 1 кубического сантиметра поглощать тепло) у алюминия ниже. Это значит, что при одинаковом объеме алюминиевая шина при КЗ нагреется быстрее и сильнее, чем медная. К тому же, у алюминия высокий коэффициент теплового расширения — при частом циклировании (нагрев-остывание) болтовые контакты «текут» и ослабевают, что требует регулярной подтяжки.

9. Интересные факты о тепловых процессах

Правило 8 градусов. В электротехнике существует эмпирическое «правило Монтзингера»: превышение рабочей температуры изоляции всего на 8 °C сверх допустимой нормы сокращает срок службы трансформатора или двигателя ровно в два раза.
Температура Солнца. Температура электрической дуги при размыкании мощных контактов может достигать 12 000 – 18 000 К. Это в 2-3 раза выше, чем температура на поверхности Солнца (около 6000 К).
Черный цвет. Радиаторы силовых трансформаторов и транзисторов часто красят в черный цвет не для красоты. Черная матовая поверхность излучает тепло на 15–25% эффективнее, чем блестящая металлическая.
Водород. Мощные турбогенераторы на электростанциях охлаждают не воздухом, а водородом. Его теплопроводность в 7 раз выше, чем у воздуха, а плотность намного ниже, что уменьшает потери на трение ротора о газ.
Серебряная ловушка. Хотя серебро проводит ток лучше меди (и греется меньше), чистое серебро в контактах используют редко. Причина — низкая температура плавления и мягкость. Чаще применяют металлокерамику «серебро-кадмий» или «серебро-вольфрам».
Скин-эффект. На частоте 50 Гц ток проникает в медь на глубину около 10 мм. Если сделать шину толщиной 50 мм, ток будет течь только по краям, а сердцевина будет работать лишь как балласт и теплоотвод, не участвуя в проводимости.
Жидкие провода. Существуют токопроводы, которые вообще не боятся перегрева контактов, потому что они жидкие. Сплав галлия, индия и олова (галинстан) используется в скользящих контактах, обеспечивая идеальное прилегание и теплоотвод.

10. FAQ: Часто задаваемые вопросы

Почему трансформаторы гудят и греются даже без нагрузки?

Даже если к трансформатору не подключены потребители, по его первичной обмотке течет ток холостого хода. Он вызывает перемагничивание стального сердечника 50 раз в секунду. Тепло выделяется из-за гистерезиса (трения магнитных доменов) и вихревых токов в стали. Гудение — это механическая вибрация (магнитострикция) того же сердечника.

Можно ли заменить медную шину на алюминиевую того же сечения?

Категорически нет. Удельное сопротивление алюминия выше, чем у меди (0,028 против 0,017 Ом·мм²/м). При том же сечении алюминиевая шина будет иметь сопротивление в 1,6 раза больше, выделит в 1,6 раза больше тепла и, скорее всего, расплавится или вызовет пожар. Для замены сечение алюминия нужно увеличить минимум на 60-70%.

Зачем нужен тепловизор при осмотре электрощита?

Тепловизор позволяет увидеть невидимое инфракрасное излучение. Он мгновенно выявляет «горячие точки» — плохие контакты, перегруженные кабели или неисправные автоматы — до того, как появится запах гари или произойдет авария. Это основной инструмент бесконтактной диагностики.

Что такое класс нагревостойкости изоляции (B, F, H)?

Это буквенная маркировка, указывающая на максимальную температуру, при которой изоляция может работать 20 000 часов. Например, класс B — 130°C, F — 155°C, H — 180°C. Если ваш двигатель класса F нагрелся до 100°C, это абсолютно нормально и безопасно.

Поможет ли вентилятор, если кабель греется в стене?

Нет. Вентилятор охлаждает только поверхность. Если кабель замурован в стену (штукатурку, бетон), теплоотдача происходит только за счет теплопроводности материала стены. Установка вентилятора в комнате не охладит жилу внутри стены. Единственное решение — снизить нагрузку или заменить кабель на большее сечение.

Заключение

Тепловой расчет — это искусство баланса между материалоемкостью и надежностью. Понимание физики процессов (скин-эффект, тепловое излучение, адиабатный нагрев) позволяет инженерам создавать безопасные электроустановки. В современных условиях, когда плотность монтажа растет, роль точных тепловых расчетов становится критической. Применение правильных методик проверки на термическую стойкость гарантирует, что при аварии оборудование не станет причиной пожара, а сможет быть восстановлено или безопасно заменено.

Нормативная база и литература

ГОСТ 30323-95 «Короткие замыкания в электроустановках. Методы расчета электродинамического и термического действия тока короткого замыкания».
ГОСТ 8024-90 «Аппараты и электротехнические устройства переменного тока на напряжение свыше 1000 В. Нормы нагрева».
ГОСТ IEC 60034-1-2014 «Машины электрические вращающиеся. Номинальные данные и рабочие характеристики» (Классификация режимов S1-S10).
ПУЭ (Правила устройства электроустановок), Издание 7. Глава 1.4.
Чунихин А.А. «Электрические аппараты»: Учебник для ВУЗов. — Фундаментальная теория аппаратостроения.
Неклепаев Б.Н. «Электрическая часть электростанций и подстанций» — Справочные материалы по расчетам КЗ.