Методы анализа линейных электрических цепей

Содержание страницы

1. Принцип наложения (суперпозиции)
2. Принцип взаимности
3. Принцип компенсации
4. Принцип линейности
5. Сравнительный анализ принципов
6. Преимущества и недостатки линейных методов
7. Интересные факты о свойствах линейных цепей
8. Часто задаваемые вопросы (FAQ)
Заключение

Линейные электрические цепи составляют основу классической электротехники. Цепь считается линейной, если она состоит из компонентов, параметры которых (сопротивление $R$, индуктивность $L$, емкость $C$) не зависят от величины протекающего через них тока или приложенного напряжения. Поведение таких цепей описывается системой линейных алгебраических или дифференциальных уравнений.

Исторически, формулировка основных свойств линейных цепей связана с развитием теории электромагнетизма в XIX веке. Принцип суперпозиции, изначально примененный в механике, был адаптирован для электричества благодаря работам Германа фон Гельмгольца (1853 г.), который также внес значительный вклад в обоснование теоремы Тевенина (эквивалентного генератора). Понимание этих свойств позволяет инженерам не просто рассчитывать схемы, но и качественно предсказывать их поведение при изменении параметров, что критично при проектировании надежных электронных устройств.

В данной статье мы подробно разберем четыре ключевых принципа, которые формируют фундамент анализа линейных цепей: наложения, взаимности, компенсации и линейности.

1. Принцип наложения (суперпозиции)

Принцип суперпозиции является прямым следствием линейности системы уравнений Кирхгофа. Он утверждает, что в любой линейной цепи, содержащей несколько независимых источников энергии, реакция (ток или напряжение) в любой ветви равна алгебраической сумме реакций, вызванных каждым источником в отдельности.

Для линейных цепей ток в $k$-ветви $I_k$ определяется как сумма частичных токов:

$$ I_k = \sum_{i=1}^{N} I_{ki} $$

где $I_{ki}$ — ток в $k$-ветви, вызванный действием только $i$-го источника.

Метод наложения

Этот принцип лежит в основе метода расчета, который позволяет свести сложную задачу с множеством источников к нескольким простым. Алгоритм метода:

Поочередно оставляем в схеме только один источник.
Остальные источники исключаем: источники ЭДС заменяем коротким замыканием ($E=0$), источники тока — разрывом цепи ($J=0$). При этом внутренние сопротивления источников остаются в схеме.
Рассчитываем частичные токи от действующего источника.
Алгебраически (с учетом направления) суммируем частичные токи для получения реального токораспределения.

Критически важно: Принцип наложения применим только к линейным величинам (ток, напряжение). Мощность $P$ зависит от тока квадратично ($P = I^2R$), поэтому мощности от частичных токов суммировать нельзя. В баланс мощностей должны входить только полные, результирующие значения токов и напряжений.

Пример 1: Расчет цепи методом наложения

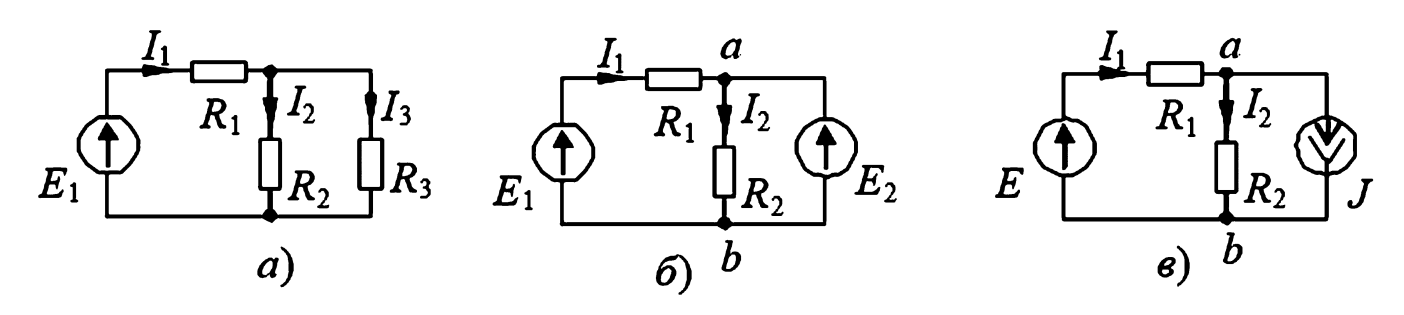
Дано: Для схемы на рисунке 1а параметры составляют: $R_1 = 2$ Ом, $R_2 = 4$ Ом, $R_3 = 6$ Ом, источник тока $J = 5$ А, источник ЭДС $E = 20$ В. Необходимо определить токи в ветвях.

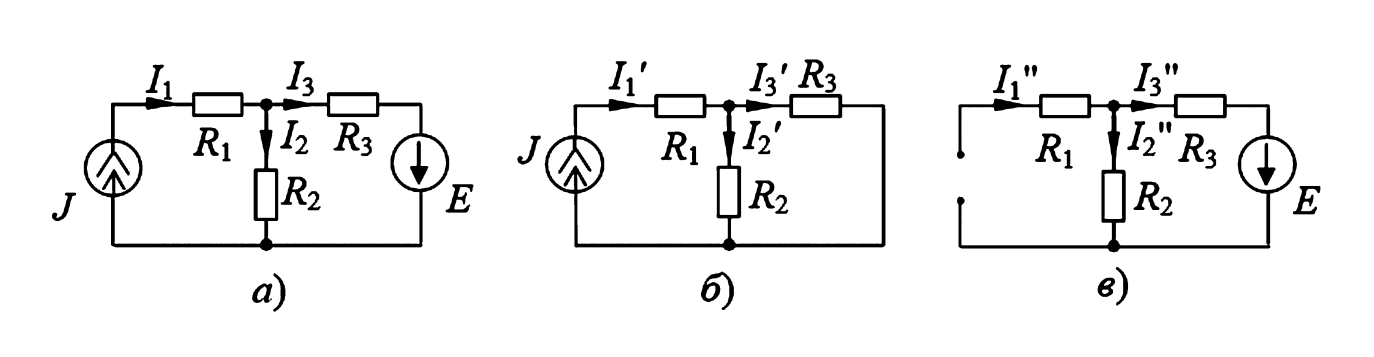
Рисунок 1. Схемы электрической цепи к примеру 1: а — исходная схема; б — источник ЭДС исключен (закорочен); в — источник тока исключен (разорван).

Решение:

Задаем положительные направления токов в исходной схеме (рис. 1а).
Этап 1 (Рис. 1б): Оставляем только источник тока $J$. Рассчитываем частичные токи (обозначены одним штрихом):
$$ I’_1 = 5 \text{ А}; \quad I’_2 = 3 \text{ А}; \quad I’_3 = 2 \text{ А} $$
(Примечание: значения получены исходя из распределения тока J по параллельным ветвям в конкретной топологии схемы).
Этап 2 (Рис. 1в): Оставляем только источник ЭДС $E$. Источник тока заменяем разрывом. Ветвь с источником тока разрывается, поэтому ток $I»_1 = 0$. Рассчитываем остальные частичные токи (обозначены двумя штрихами):
$$ I»_1 = 0 \text{ А}; \quad I»_2 = -2 \text{ А}; \quad I»_3 = 2 \text{ А} $$
Этап 3: Суммируем частичные токи для получения истинных значений:
$$ I_1 = I’_1 + I»_1 = 5 + 0 = 5 \text{ А} $$
$$ I_2 = I’_2 + I»_2 = 3 + (-2) = 1 \text{ А} $$
$$ I_3 = I’_3 + I»_3 = 2 + 2 = 4 \text{ А} $$
Проверка балансом мощностей:
$$ P_{ист} = E \cdot I_3 + J \cdot U_{J} $$
$$ P_{потр} = I_1^2 R_1 + I_2^2 R_2 + I_3^2 R_3 $$
Расчет показывает $P_{ист} = P_{потр} = 150$ Вт. Баланс сошелся.

2. Принцип взаимности

Принцип взаимности (или обратимости) свойственен только линейным пассивным цепям (не содержащим зависимых источников). Он гласит: ток в $k$-ветви $I_k$, вызванный единственным источником ЭДС $E_m$, находящимся в $m$-ветви, будет равен току $I_m$ в $m$-ветви, если тот же источник $E_m$ перенести в $k$-ветвь.

Математически это записывается через равенство взаимных проводимостей:

$$ I_k = E_m \cdot g_{km} \quad \text{и} \quad I_m = E_k \cdot g_{mk} $$
$$ \text{Если } E_m = E_k \text{, то } I_k = I_m \implies g_{km} = g_{mk} $$

Это свойство основано на симметрии матрицы узловых проводимостей или контурных сопротивлений пассивной цепи. При использовании принципа взаимности важно следить за соответствием направлений ЭДС и токов в ветвях — они должны быть согласованы одинаково в обоих случаях.

3. Принцип компенсации

Принцип компенсации позволяет заменить любой пассивный элемент цепи активным источником без изменения токораспределения во всей остальной цепи. В любой электрической цепи сопротивление $R$, по которому протекает ток $I$, можно заменить:

Источником ЭДС $E_k$ с напряжением, равным падению напряжения на этом сопротивлении ($E_k = I \cdot R$), и направленным навстречу току.
Источником тока $J_k$, равным току в этом сопротивлении ($J_k = I$) и направленным в ту же сторону.

Теоретически это следует из законов Кирхгофа: перенос слагаемого $IR$ из одной части уравнения в другую эквивалентен замене пассивного элемента на источник ЭДС.

Пример 2: Применение принципа компенсации

Дано: В схеме (рис. 2а) $E_1 = 5$ В, $R_1 = 1$ Ом, $R_2 = 2$ Ом, $R_3 = 1$ Ом. Требуется заменить $R_3$ эквивалентными источниками.

Рисунок 2. Схема к примеру 2: а — исходная; б — с компенсирующим источником ЭДС; в — с компенсирующим источником тока.

Решение:

Определяем исходные токи в схеме (например, методом контурных токов):
$$ I_1 = 3 \text{ А}; \quad I_2 = 1 \text{ А}; \quad I_3 = 2 \text{ А} $$
Компенсация ЭДС (Рис. 2б): Заменяем $R_3$ источником ЭДС $E_k$. Его величина равна падению напряжения на $R_3$:
$$ E_k = U_{R3} = I_3 \cdot R_3 = 2 \text{ А} \cdot 1 \text{ Ом} = 2 \text{ В} $$
Направляем $E_k$ навстречу исходному току $I_3$.
Компенсация током (Рис. 2в): Заменяем ветвь с $R_3$ источником тока $J_k$:
$$ J_k = I_3 = 2 \text{ А} $$
При такой замене проверка по первому закону Кирхгофа для узла дает: $I_1 — I_2 — J_k = 3 — 1 — 2 = 0$. Токораспределение не изменилось.

4. Принцип линейности

Это обобщающее свойство гласит, что в линейной цепи любые два значения токов или напряжений связаны между собой линейной зависимостью вида $y = ax + b$. Если в цепи изменяется только один параметр (например, одна ЭДС или одно сопротивление), то ток $I_1$ в одной ветви будет линейно зависеть от тока $I_2$ в другой ветви:

$$ I_1 = k \cdot I_2 + m $$
$$ U_1 = c \cdot U_2 + d $$

Если изменяются два параметра, зависимость принимает вид $y = ax + bz + c$.

Коэффициенты ($a, b, k, m$ и др.) можно определить экспериментально или расчетом, зная параметры режима цепи в двух разных точках. Это позволяет моделировать цепь как «черный ящик», не зная её внутренней структуры.

Пример 3: Использование свойства линейности

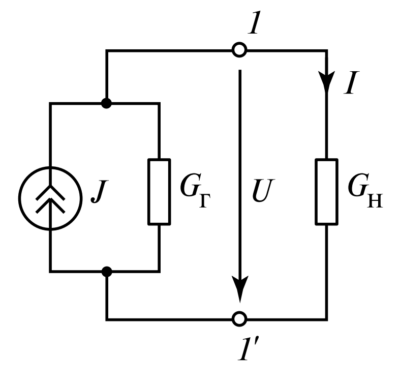
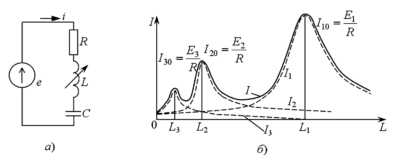
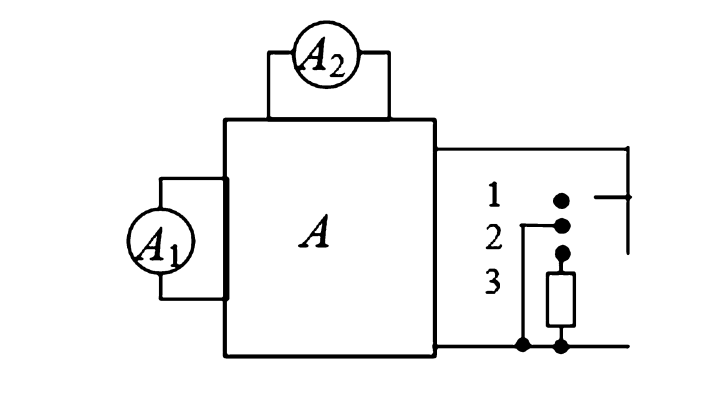
Дано: В схеме с переключателем (рис. 3) проведены два опыта:

1. Холостой ход (положение 1): $I_{1xx} = 1$ А, $I_{2xx} = 5$ А.

2. Короткое замыкание (положение 2): $I_{1к} = 2$ А, $I_{2к} = 4$ А.

Задача: Определить ток $I_1$ в третьем произвольном режиме, если известно, что $I_2 = 4.5$ А.

Рисунок 3. Электрическая схема к примеру 3 с изменяемой нагрузкой.

Решение:

Используем линейную зависимость $I_1 = a \cdot I_2 + b$. Составим систему уравнений по двум известным опытам:
$$ \begin{cases} 1 = a \cdot 5 + b \quad (\text{из опыта ХХ}) \\ 2 = a \cdot 4 + b \quad (\text{из опыта КЗ}) \end{cases} $$
Решаем систему. Вычитаем второе уравнение из первого:
$$ 1 — 2 = 5a — 4a \implies -1 = a $$
Подставляем $a = -1$ в первое уравнение:
$$ 1 = (-1) \cdot 5 + b \implies b = 6 $$
Получили уравнение связи: $I_1 = 6 — I_2$.
Определяем искомый ток для третьего режима при $I_2 = 4.5$ А:
$$ I_1 = 6 — 4.5 = 1.5 \text{ А} $$

5. Сравнительный анализ принципов

Принцип	Суть принципа	Основное применение	Ограничения
Наложения (Суперпозиции)	Реакция цепи есть сумма реакций от каждого источника в отдельности.	Расчет цепей с множеством источников, особенно разных частот.	Не применим для расчета мощностей (нелинейная зависимость).
Взаимности	Ток не изменится при переносе ЭДС из ветви A в ветвь B и наоборот.	Проверка правильности расчетов, упрощение анализа четырехполюсников.	Только для пассивных цепей (без зависимых источников и усилителей).
Компенсации	Пассивный элемент можно заменить источником с тем же напряжением/током.	Анализ чувствительности цепи, доказательство других теорем (Тевенина).	Требует предварительного знания тока или напряжения на заменяемом элементе.
Линейности	Параметры режима в разных ветвях связаны линейным уравнением $y=ax+b$.	Экспериментальное определение параметров «черного ящика», экстраполяция данных.	Справедлив только пока элементы цепи остаются на линейном участке ВАХ.

6. Преимущества и недостатки линейных методов

Преимущества

Упрощение расчетов: Сложные задачи разбиваются на простые подзадачи.
Аналитичность: Дают общее решение в виде формул, а не только численный результат.
Наглядность: Позволяют оценить вклад каждого источника в общий режим работы.
Универсальность: Работают как для постоянного, так и для переменного тока (в комплексной форме).

Недостатки и ограничения

Только линейные цепи: Не работают при наличии диодов, транзисторов в нелинейном режиме, насыщающихся катушек.
Трудоемкость при ручном счете: Для цепи с $N$ источниками нужно решить $N$ отдельных задач (метод наложения).
Ошибка с мощностью: Частая ошибка новичков — попытка применить суперпозицию к расчету мощности.

7. Интересные факты о свойствах линейных цепей

Разные частоты: Принцип суперпозиции — единственный способ ручного расчета цепей, где действуют источники с разными частотами (например, постоянный ток + гармоника 50 Гц).
Необратимость гираторов: Существуют специальные пассивные элементы — гираторы, которые нарушают принцип взаимности, что используется в СВЧ-технике.
Основа SPICE: Современные симуляторы (подобные SPICE) рассчитывают нелинейные цепи, заменяя их на каждом малом шаге времени линейными эквивалентными схемами, используя принцип линеаризации.
Связь с механикой: Многие из этих принципов имеют полные аналоги в механике (например, сложение сил в статике).
Теорема Телледжена: Является фундаментальным обобщением законов Кирхгофа и работает даже для нелинейных цепей, в отличие от рассмотренных выше принципов.
«Черный ящик»: Благодаря принципу линейности инженеру достаточно сделать всего два замера на выводах неизвестного линейного блока, чтобы полностью описать его внешние характеристики.
Ограничение реального мира: В реальности абсолютно линейных элементов не существует. Резистор нагревается и меняет сопротивление, катушка насыщается. Линейность — это всегда идеализация, допустимая в определенных границах.

8. Часто задаваемые вопросы (FAQ)

В: Почему нельзя применять принцип наложения для расчета мощности?

О: Мощность зависит от квадрата тока: $P = i^2R$. Если $i = i_1 + i_2$, то $P = (i_1 + i_2)^2 R = i_1^2 R + i_2^2 R + 2i_1i_2 R$. Слагаемое $2i_1i_2 R$ теряется, если просто складывать мощности от отдельных источников.

В: Работает ли принцип взаимности в цепях с операционными усилителями?

О: Нет, как правило, не работает. Операционный усилитель содержит зависимые источники, которые делают цепь активной и необратимой (сигнал проходит только со входа на выход).

В: Что делать, если в цепи есть зависимые источники, при использовании метода наложения?

О: Зависимые (управляемые) источники нельзя «отключать» так же, как независимые. Они должны оставаться в схеме при расчете действия каждого независимого источника.

В: Где на практике применяется принцип компенсации?

О: Он активно используется при измерении параметров активных двухполюсников методом замещения, а также служит теоретической базой для доказательства теоремы об эквивалентном генераторе.

В: Можно ли использовать эти принципы для цепей переменного тока?

О: Да, абсолютно все перечисленные принципы справедливы для цепей синусоидального тока, если проводить расчеты в комплексной форме (используя комплексные сопротивления $Z$).

В: Какова точность расчетов при использовании свойства линейности?

О: Точность зависит только от точности исходных замеров. Математически метод точен. Ошибки возникают, если реальный элемент выходит за пределы своего линейного диапазона.

В: Какой метод лучше всего подходит для компьютерного моделирования?

О: Для машинного расчета чаще используют методы узловых потенциалов, которые формируют систему линейных уравнений, решаемую матричными методами. Но эти уравнения сами базируются на свойствах линейности.

Заключение

Свойства линейных электрических цепей — наложения, взаимности, компенсации и линейности — это не просто абстрактные теоретические концепции, а мощный практический инструментарий инженера. Глубокое понимание этих принципов позволяет эффективно анализировать сложные схемы, выполнять проверку расчетов, полученных с помощью САПР, и интуитивно находить изящные решения нетривиальных электротехнических задач. Несмотря на развитие вычислительной техники, эти фундаментальные законы остаются «языком», на котором инженеры думают о схемах.

Нормативная база и литература

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Устанавливает базовую терминологию, включая определения линейных цепей и пассивных/активных элементов.
ГОСТ 19880-74 «Электротехника. Основные понятия. Термины и определения» (исторический, но фундаментальный стандарт).
Бессонов Л.А. «Теоретические основы электротехники. Электрические цепи» — классический учебник, детально описывающий данные принципы.