Связь заряда и напряженности поля: Закон Кулона, Теорема Гаусса

Содержание страницы

1. Закон Кулона: Основа электростатики
2. Напряженность электрического поля точечного заряда
3. Теорема Гаусса: Интегральная связь поля и заряда
4. Сравнение Закона Кулона и Теоремы Гаусса
5. Пример: Применение Теоремы Гаусса для расчета поля заряженного шара
6. Преимущества, недостатки и обобщение законов
7. Интересные факты по теме
8. Часто задаваемые вопросы (FAQ)
Заключение

Электрическое поле — основная форма материи, описывающая силовое взаимодействие между электрическими зарядами. Связь между источником (зарядом) и самим полем количественно выражается двумя ключевыми законами электростатики: Законом Кулона и Теоремой Гаусса.

Закон Кулона определяет силу, действующую между двумя точечными зарядами, в то время как Теорема Гаусса предоставляет более общий метод для нахождения напряженности поля, связывая поток электрического поля через замкнутую поверхность с суммарным зарядом внутри этой поверхности.

Основы электростатики были заложены в 1780-х годах Шарлем-Огюстеном де Кулоном, который экспериментально установил закон взаимодействия точечных зарядов. Позднее, в 1830-х годах (хотя математический аппарат был разработан им ранее), Карл Фридрих Гаусс сформулировал свою теорему, которая стала одним из четырех фундаментальных уравнений электродинамики — уравнений Максвелла.

1. Закон Кулона: Основа электростатики

Поскольку основным свойством электрического поля является его силовое воздействие на заряженную частицу, представляет интерес установление связи между зарядами частиц и основной характеристикой поля — его напряженностью. Для выявления такой связи воспользуемся экспериментально установленным законом Кулона.

Этот закон описывает силовое взаимодействие двух точечных частиц с зарядами $Q$ и $Q_0$, расположенных в вакууме (пустоте) на расстоянии $R$ одна от другой (Рисунок 1). На частицу с зарядом $Q_0$ со стороны частицы с зарядом $Q$ действует сила, значение которой:

Прямо пропорционально произведению модулей зарядов $|Q|$ и $|Q_0|$.
Обратно пропорционально квадрату расстояния между ними $R^2$.

Сила направлена по оси, соединяющей частицы. Она является силой отталкивания, если заряды $Q$ и $Q_0$ имеют одинаковые знаки, и силой притяжения, если заряды $Q$ и $Q_0$ имеют разные знаки.

Рисунок 1. Иллюстрация закона Кулона: силовое воздействие частицы с зарядом $Q$ на частицу с зарядом $Q_0$ (показан случай одноименных зарядов).

В векторной форме закон Кулона записывается следующим образом:

$$ \vec{F} = \frac{1}{4 \pi \varepsilon_0} \frac{Q Q_0}{R^2} \left( \frac{\vec{R}}{R} \right) $$

(Формула 1)

Здесь:

$\vec{F}$ — вектор силы, действующей на заряд $Q_0$.
$Q$ и $Q_0$ — величины зарядов (со знаками).
$R$ — расстояние между зарядами.
$\vec{R}$ — вектор, направленный от заряда $Q$ к заряду $Q_0$.
$\left( \frac{\vec{R}}{R} \right)$ — единичный безразмерный вектор (орт), задающий направление.
$\varepsilon_0$ — электрическая постоянная (диэлектрическая проницаемость вакуума), определяемая как:

$$ \varepsilon_0 \approx 8.854 \times 10^{-12} \text{ Ф/м} $$

(Формула 2)

Примечание о стандартизации: Значение электрической постоянной $\varepsilon_0$, а также определения всех основных единиц СИ (Международной системы единиц), таких как Кулон (Кл), Метр (м) и Фарад (Ф), в Российской Федерации регламентируются ГОСТ 8.417-2024 «Государственная система обеспечения единства измерений. Единицы величин». Этот стандарт гармонизирован с международными принципами СИ.

Замена в приведенной формулировке заряда $Q$ на заряд $Q_0$, а заряда $Q_0$ на заряд $Q$ (и $\vec{R}$ на $-\vec{R}$) определит силу, действующую на заряд $Q$ со стороны заряда $Q_0$, в полном соответствии с третьим законом Ньютона.

2. Напряженность электрического поля точечного заряда

Закон Кулона позволяет ввести количественную характеристику самого поля. Напряженность электрического поля $\vec{E}$ в данной точке — это векторная физическая величина, равная отношению силы $\vec{F}$, действующей на пробный точечный заряд $Q_0$, помещенный в эту точку, к величине этого заряда:

$$ \vec{E} = \frac{\vec{F}}{Q_0} $$

Зная силу (Формула 1), можно найти напряженность поля, которую создает частица с зарядом $Q$ в точке расположения частицы с зарядом $Q_0$:

$$ \vec{E} = \frac{1}{Q_0} \left[ \frac{1}{4 \pi \varepsilon_0} \frac{Q Q_0}{R^2} \left( \frac{\vec{R}}{R} \right) \right] = \frac{1}{4 \pi \varepsilon_0} \frac{Q}{R^2} \left( \frac{\vec{R}}{R} \right) $$

(Формула 3)

Эта формула описывает электрическое поле, создаваемое одиночным точечным зарядом $Q$ в вакууме. Напряженность поля убывает обратно пропорционально квадрату расстояния от заряда.

3. Теорема Гаусса: Интегральная связь поля и заряда

Закон Кулона неудобен, если нужно рассчитать поле от множества зарядов или от заряженного тела (например, пластины или сферы). В таких случаях используется более мощный и элегантный подход — Теорема Гаусса.

Эта теорема оперирует понятием потока вектора напряженности ($\Phi_E$) сквозь произвольную замкнутую поверхность (называемую «гауссовой поверхностью»). Поток можно интуитивно представить как «количество» линий напряженности поля, пронизывающих эту поверхность.

Рассмотрим вывод теоремы для точечного заряда $Q$, помещенного в центр сферы радиусом $R$ (Рисунок 2).

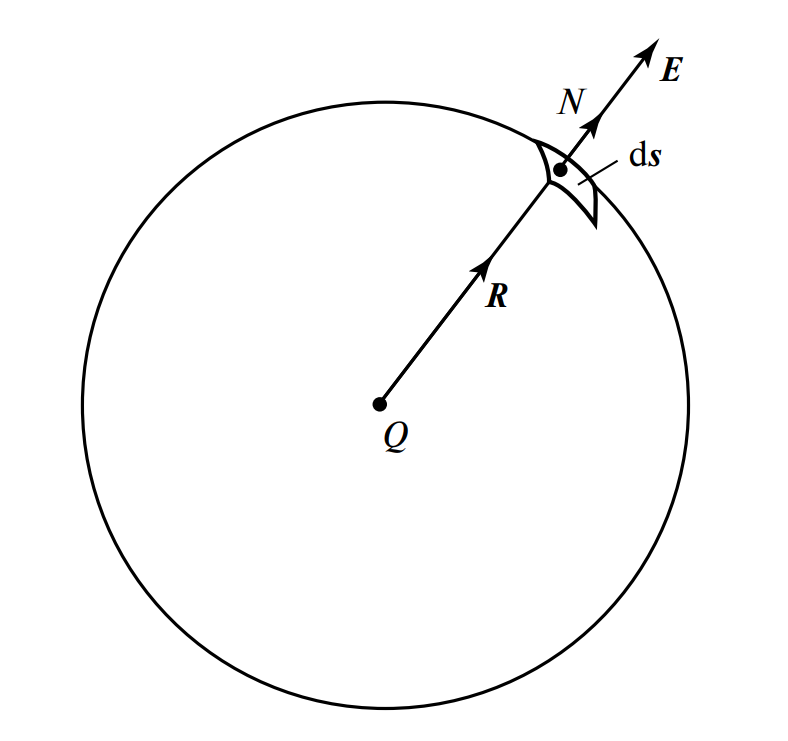
Рисунок 2. К вычислению потока вектора напряженности $\vec{E}$ через замкнутую сферическую поверхность $S$.

По определению, полный поток $\Phi_E$ — это интеграл вектора $\vec{E}$ по всей площади замкнутой поверхности $S$:

$$ \Phi_E = \oint_S \vec{E} \cdot d\vec{s} $$

Где $d\vec{s}$ — вектор элементарной площадки, равный по модулю $ds$ и направленный по нормали $\vec{N}$ наружу.

В нашем случае (сфера с зарядом в центре):

Вектор напряженности $\vec{E}$ (Формула 3) в любой точке сферы направлен радиально, так же как и вектор нормали $d\vec{s}$. Поэтому их скалярное произведение $\vec{E} \cdot d\vec{s} = E \, ds \cdot \cos(0) = E \, ds$.
Модуль напряженности $E$ во всех точках сферы одинаков (т.к. $R$ = const) и равен $E = \frac{Q}{4 \pi \varepsilon_0 R^2}$.

Поскольку $E$ — константа на поверхности сферы, ее можно вынести за знак интеграла:

$$ \Phi_E = \oint_S E \, ds = E \oint_S ds $$

Интеграл $\oint_S ds$ — это просто сумма всех элементарных площадок, т.е. полная площадь поверхности сферы, которая равна $S = 4 \pi R^2$.

Подставим значения $E$ и $S$:

$$ \Phi_E = \left( \frac{Q}{4 \pi \varepsilon_0 R^2} \right) \cdot (4 \pi R^2) = \frac{Q}{\varepsilon_0} $$

Мы получили результат, который не зависит от радиуса $R$ сферы. Карл Гаусс доказал, что этот результат верен для любой замкнутой поверхности произвольной формы и для любого распределения зарядов внутри нее.

Теорема Гаусса: Поток вектора напряженности электрического поля $\vec{E}$ сквозь произвольную замкнутую поверхность $S$ в вакууме равен алгебраической сумме зарядов ($Q_{вн}$), заключенных внутри этой поверхности, деленной на электрическую постоянную $\varepsilon_0$.

$$ \Phi_E = \oint_S \vec{E} \cdot d\vec{s} = \frac{Q_{вн}}{\varepsilon_0} $$

(Формула 4)

Примечание о терминах: Понятия «напряженность электрического поля», «электрический заряд» и «электрическое поле» являются базовыми в электротехнике. Их формальные определения и связь с другими физическими величинами закреплены в ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий».

4. Сравнение Закона Кулона и Теоремы Гаусса

Оба закона описывают одно и то же явление, но с разных точек зрения. Их ключевые различия и области применения приведены в таблице 1.

**Таблица 1.** Сравнительные характеристики Закона Кулона и Теоремы Гаусса
Характеристика	Закон Кулона	Теорема Гаусса
Основное назначение	Расчет силы $\vec{F}$ между дискретными (точечными) зарядами.	Расчет напряженности $\vec{E}$ от распределенных зарядов.
Форма закона	Векторный, алгебраический. Описывает локальное взаимодействие.	Интегральный. Описывает свойство поля на замкнутой поверхности.
Ключевая концепция	Сила $\vec{F}$.	Поток $\Phi_E$.
Основное применение	Задачи на взаимодействие 2-3 точечных зарядов.	Задачи с высокой степенью симметрии (сферы, цилиндры, плоскости).
Сложность	Прост для точечных зарядов, но требует сложного векторного суммирования (или интегрирования) для тел.	Бесполезна для расчета $\vec{E}$ при отсутствии симметрии, но тривиально решает сложные симметричные задачи.

5. Пример: Применение Теоремы Гаусса для расчета поля заряженного шара

Применим теорему Гаусса для расчета поля равномерно заряженного шара с общим зарядом $Q > 0$, радиусом $R_0$ и диэлектрической проницаемостью $\varepsilon = \varepsilon_0$ (Рисунок 3а).

Рисунок 3. Электрическое поле заряженного шара: (а) — геометрия задачи, показывающая шар с радиусом $R_0$ и гауссову поверхность радиусом $R$; (б) — график зависимости напряженности $E$ от расстояния $R$ от центра шара.

5.1. Поле вне шара ($R \ge R_0$)

Рассмотрим в качестве гауссовой поверхности сферу радиусом $R \ge R_0$ с центром, совпадающим с центром шара. Из соображений симметрии, вектор $\vec{E}$ в любой точке этой сферы направлен по радиусу (как и $d\vec{s}$) и одинаков по модулю $E$.

Тогда левая часть теоремы Гаусса (Формула 4) упрощается:

$$ \oint_S \vec{E} \cdot d\vec{s} = \oint_S E \, ds = E \oint_S ds = E \cdot (4 \pi R^2) $$

Заряд, заключенный внутри этой поверхности, — это весь заряд шара, $Q_{вн} = Q$.

Применяем теорему Гаусса:

$$ E \cdot (4 \pi R^2) = \frac{Q}{\varepsilon_0} $$

Отсюда, напряженность поля вне шара:

$$ E = \frac{Q}{4 \pi \varepsilon_0 R^2} $$

(Формула 5)

Вывод: Вне заряженного шара поле такое же, как у точечного заряда $Q$, помещенного в его центр. Значение напряженности убывает обратно пропорционально квадрату расстояния $R^2$.

5.2. Поле внутри шара ($R < R_0$)

Теперь выберем гауссову поверхность в виде сферы радиусом $R < R_0$ (внутри шара). Левая часть теоремы Гаусса остается такой же: $\oint \vec{E} \cdot d\vec{s} = E \cdot (4 \pi R^2)$.

Однако правая часть меняется. Нам нужно найти заряд $Q’$, заключенный только внутри сферы радиусом $R$.

Сначала найдем объемную плотность заряда $\rho$ (предполагая равномерное распределение):

$$ \rho = \frac{\text{Полный заряд}}{\text{Полный объем}} = \frac{Q}{V_0} = \frac{Q}{\frac{4}{3} \pi R_0^3} $$

(Формула 6)

Теперь заряд $Q’$ внутри гауссовой поверхности объемом $V’ = \frac{4}{3} \pi R^3$ равен:

$$ Q’ = \rho \cdot V’ = \left( \frac{Q}{\frac{4}{3} \pi R_0^3} \right) \cdot \left( \frac{4}{3} \pi R^3 \right) = Q \left( \frac{R^3}{R_0^3} \right) $$

Применяем теорему Гаусса для $R < R_0$:

$$ E \cdot (4 \pi R^2) = \frac{Q’}{\varepsilon_0} = \frac{1}{\varepsilon_0} Q \left( \frac{R^3}{R_0^3} \right) $$

Решаем относительно $E$:

$$ E = \frac{Q R^3}{4 \pi \varepsilon_0 R^2 R_0^3} = \frac{Q R}{4 \pi \varepsilon_0 R_0^3} $$

(Формула 7)

Вывод: Внутри шара напряженность $E$ растет линейно с ростом расстояния $R$ от центра (от $E=0$ при $R=0$).

Максимальное значение напряженности достигается на поверхности шара при $R = R_0$:

$$ E_{max} = \frac{Q R_0}{4 \pi \varepsilon_0 R_0^3} = \frac{Q}{4 \pi \varepsilon_0 R_0^2} $$

(Формула 8)

График изменения напряженности $E$ в зависимости от $R$ приведен на Рисунке 3б.

6. Преимущества, недостатки и обобщение законов

Рассмотренный материал показывает, что каждая заряженная частица или тело является источником электрического поля. Закон Кулона и Теорема Гаусса — это инструменты для его расчета, и у каждого есть свои сильные и слабые стороны.

Закон Кулона

Преимущества:

Интуитивная понятность и прямое применение для расчета сил.
Не требует симметрии; позволяет рассчитать силу в любой конфигурации точечных зарядов.

Недостатки:

Требует сложного векторного суммирования (или интегрирования) при работе с большим количеством зарядов или с распределенными зарядами.
Маскирует общие свойства поля (такие как поток).

Теорема Гаусса

Преимущества:

Чрезвычайно упрощает расчеты $\vec{E}$ для систем с высокой симметрией (сферы, бесконечные цилиндры, бесконечные плоскости).
Является фундаментальным законом (одно из уравнений Максвелла), показывающим, что источниками поля являются заряды.

Недостатки:

Практически бесполезна для прямого расчета $\vec{E}$, если в задаче отсутствует симметрия (например, для диполя или заряженного куба).
Требует понимания векторного анализа (поток, поверхностный интеграл).

Обобщение на диэлектрические среды

Закон Кулона и теорема Гаусса могут быть обобщены на случай, когда поле рассматривается не в вакууме, а в некоторой однородной диэлектрической среде. Для этого электрическую постоянную $\varepsilon_0$ заменяют на абсолютную диэлектрическую проницаемость среды $\varepsilon$, где $\varepsilon = \varepsilon_0 \varepsilon_r$ ($\varepsilon_r$ — относительная диэлектрическая проницаемость, показывающая, во сколько раз среда ослабляет поле).

Математические записи при этом примут вид:

Закон Кулона в среде:

$$ \vec{F} = \frac{1}{4 \pi \varepsilon} \frac{Q Q_0}{R^2} \left( \frac{\vec{R}}{R} \right) $$

(Формула 9)

Теорема Гаусса в среде (для вектора $\vec{E}$):

$$ \oint_S \vec{E} \cdot d\vec{s} = \frac{Q_{вн}}{\varepsilon} $$

(Формула 10)

Для корректного использования этих обобщений необходимо детальное изучение поляризации диэлектриков и введение вектора электрического смещения $\vec{D}$.

7. Интересные факты по теме

Фундаментальность: Теорема Гаусса для электрического поля (в несколько иной форме) является первым из четырех знаменитых уравнений Максвелла, составляющих полную основу классической электродинамики.
Связь с гравитацией: Закон Кулона имеет точно такую же математическую форму «обратных квадратов» ($1/R^2$), что и Закон всемирного тяготения Ньютона. Это указывает на глубокую геометрическую природу обоих полей.
Точность «двойки»: Точность показателя степени $2$ в законе Кулона ($1/R^2$) проверялась экспериментально. Современные измерения показывают, что он равен $2 \pm 10^{-16}$, что делает его одним из самых точно установленных законов физики.
Линии Фарадея: Концепция «потока» была введена Майклом Фарадеем в виде наглядных «силовых линий». Теорема Гаусса в этой модели гласит, что число линий, исходящих из замкнутой поверхности, прямо пропорционально заряду внутри нее.
Нулевой поток: Если поместить заряд *снаружи* замкнутой поверхности, то поток через нее будет равен нулю. Любая силовая линия, входящая в поверхность, обязательно из нее и выйдет в другом месте.

8. Часто задаваемые вопросы (FAQ)

1. Что произойдет, если заряд находится не в центре сферы в примере с Теоремой Гаусса?

Ответ: Сама теорема $\oint \vec{E} \cdot d\vec{s} = Q/\varepsilon_0$ останется верной. Однако расчет $\vec{E}$ усложнится. Поле $\vec{E}$ перестанет быть одинаковым во всех точках сферы и не будет везде перпендикулярно ей. Поэтому вынести $E$ из-под интеграла не получится, и теорема Гаусса в такой форме станет бесполезной для нахождения $\vec{E}$ (хотя сам поток мы все еще знаем).

2. Почему в Законе Кулона и Теореме Гаусса используется $\varepsilon_0$?

Ответ: Электрическая постоянная $\varepsilon_0$ — это фундаментальный коэффициент пропорциональности в системе СИ. Она связывает механические единицы (ньютон, метр) с электрическими (кулон). Ее наличие необходимо для того, чтобы формулы давали правильные численные ответы в принятых нами единицах измерения.

3. Теорема Гаусса всегда верна, или только для симметричных задач?

Ответ: Теорема Гаусса абсолютно всегда верна. Поток через любую воображаемую замкнутую поверхность всегда в точности равен $\frac{Q_{вн}}{\varepsilon_0}$. Однако она полезна для расчета $\vec{E}$ только в задачах с высокой симметрией (сферической, цилиндрической, плоской), где мы можем упростить интеграл $\oint \vec{E} \cdot d\vec{s}$ до $E \cdot S$.

4. Можно ли рассчитать поле заряженной пластины с помощью Закона Кулона?

Ответ: Да, но это очень сложная математическая задача. Потребуется разбить пластину на бесконечно малые точечные заряды $dQ$, рассчитать поле $d\vec{E}$ от каждого из них в нужной точке по Закону Кулона, а затем проинтегрировать (векторно!) все эти поля по всей поверхности пластины. С помощью Теоремы Гаусса эта же задача решается в несколько строк.

5. Что такое «диэлектрическая проницаемость» $\varepsilon$?

Ответ: Это характеристика материала (диэлектрика). Когда диэлектрик помещают во внешнее поле $\vec{E}$, его молекулы поляризуются, создавая собственное внутреннее поле, направленное против внешнего. В результате результирующее поле внутри материала ослабляется. Величина $\varepsilon$ (или $\varepsilon_r = \varepsilon / \varepsilon_0$) как раз и показывает, во сколько раз ослабляется поле в этом веществе.

Заключение

Закон Кулона и Теорема Гаусса являются двумя взаимодополняющими формулировками одного и того же фундаментального принципа — связи электрического заряда и порождаемого им электрического поля. Закон Кулона предоставляет прямой и интуитивно понятный метод расчета сил в простых конфигурациях точечных зарядов.

Теорема Гаусса, в свою очередь, предлагает более глубокий и универсальный взгляд, связывая общую структуру поля (через поток) с его источником (зарядом). Она не только служит мощнейшим инструментом для решения сложных задач в условиях симметрии, но и выступает в качестве одного из краеугольных камней всей современной теории электромагнетизма.

Нормативная база

ГОСТ 8.417-2024. Государственная система обеспечения единства измерений. Единицы величин.
ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий.

Связь электрического заряда и поля: Закон Кулона и Теорема Гаусса