Синусоидальный ток в идеальном индуктивном элементе

Содержание страницы

1. Связь напряжения и тока: Физический смысл
2. Индуктивное сопротивление и фазовые соотношения
3. Мгновенная мощность и энергетические процессы
4. Сравнение параметров элементов цепи
5. Преимущества и недостатки модели «Идеальная индуктивность»
6. Интересные факты
7. FAQ: Часто задаваемые вопросы
Заключение

Идеальный индуктивный элемент (индуктивность) — это теоретическая модель катушки, в которой отсутствует активное сопротивление (потери на нагрев) и межвитковая емкость. Вся энергия расходуется исключительно на создание магнитного поля.

Краткая история: Фундамент для понимания этих процессов заложили Майкл Фарадей (открывший электромагнитную индукцию в 1831 году) и Джозеф Генри. Их работы позволили описать, как переменный ток порождает электродвижущую силу самоиндукции, препятствующую изменению тока.

1. Связь напряжения и тока: Физический смысл

Чтобы понять процессы в цепях переменного тока, необходимо рассмотреть взаимосвязь мгновенных значений напряжения \( u \) и тока \( i \). В идеальном индуктивном элементе с индуктивностью \( L \) эта связь, согласно законам коммутации и электромагнитной индукции, определяется формулой:

u = L \frac{di}{dt}

Это фундаментальное уравнение означает, что напряжение на катушке пропорционально скорости изменения тока, а не самому току. Если ток синусоидальный и описывается выражением \( i(t) = I_m \sin(\omega t + \psi_i) \), то, продифференцировав его по времени, мы получим выражение для напряжения.

Математический вывод

Подставим функцию тока в формулу напряжения:

u(t) = L \frac{d}{dt} [I_m \sin(\omega t + \psi_i)]

Взяв производную синуса, получаем косинус и множитель \( \omega \) (угловая частота):

u(t) = \omega L I_m \cos(\omega t + \psi_i)

Используя тригонометрические формулы приведения, перейдем от косинуса к синусу, добавив \( 90^\circ \):

u(t) = U_m \sin(\omega t + \psi_i + 90^\circ) = U_m \sin(\omega t + \psi_u)

2. Индуктивное сопротивление и фазовые соотношения

Из полученных выше формул следует определение амплитуды напряжения:

U_m = \omega L I_m = X_L I_m

Здесь вводятся ключевые понятия электротехники:

\( X_L = \omega L \) — индуктивное сопротивление (измеряется в Омах). Оно показывает, насколько сильно элемент препятствует протеканию переменного тока. Чем выше частота \( \omega \), тем выше сопротивление.
\( B_L = \frac{1}{X_L} \) — индуктивная проводимость (измеряется в Сименсах).

Важно запомнить: Сдвиг фаз
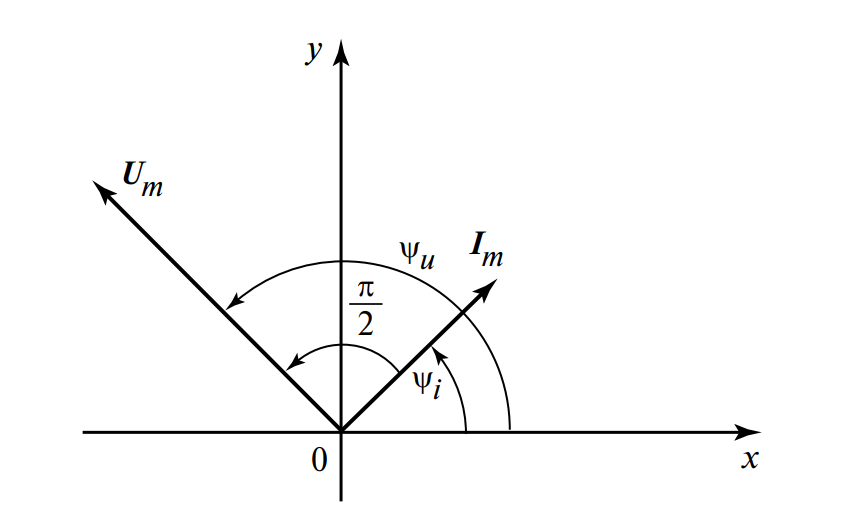
Начальная фаза напряжения определяется как \( \psi_u = \psi_i + 90^\circ \). Это означает, что напряжение на идеальной индуктивности опережает ток по фазе на \( 90^\circ \) (или на \( \pi/2 \) радиан).

Сдвиг по фазе между напряжением и током составляет:

\phi = \psi_u — \psi_i = \frac{\pi}{2}

Также можно выразить ток через напряжение, учитывая отставание тока:

i(t) = B_L U_m \sin(\omega t + \psi_u — \frac{\pi}{2})

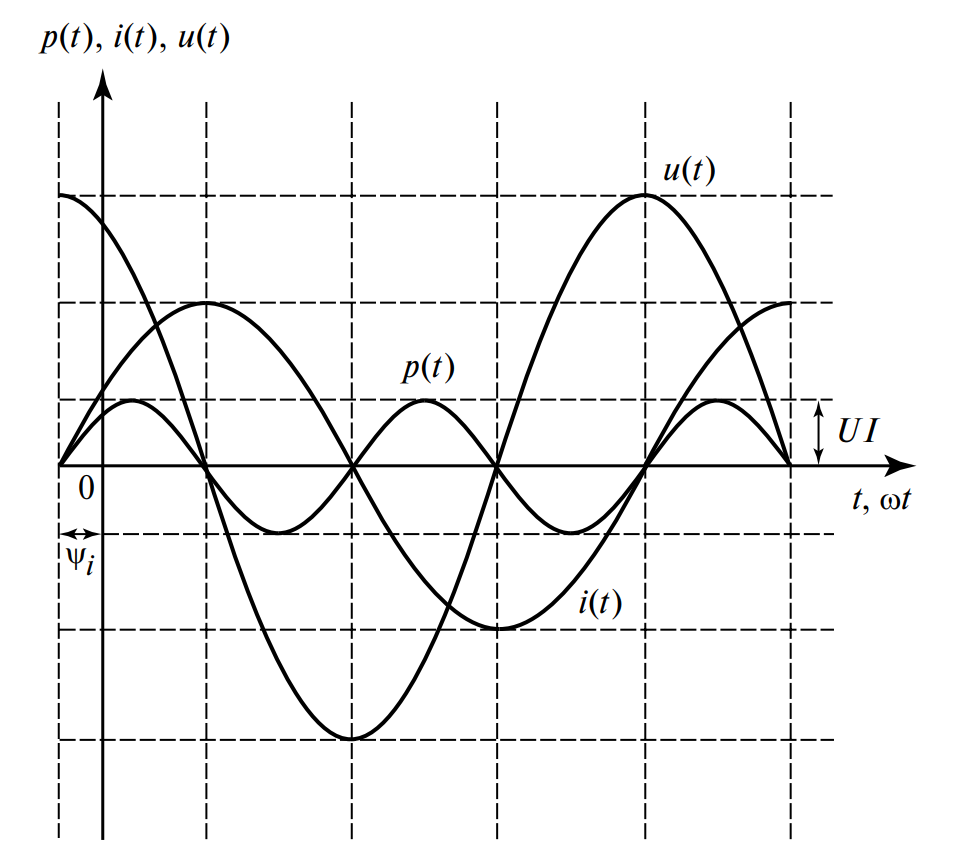
Графики тока, напряжения и мощности в индуктивном элементе

Рис. 1. Временные диаграммы мгновенных значений в индуктивном элементе.

Описание Рис. 1: На графике представлены зависимости \( u(t) \), \( i(t) \) и \( p(t) \). Синусоида тока \( i(t) \) отстает от синусоиды напряжения \( u(t) \) на четверть периода. Кривая мгновенной мощности \( p(t) \) имеет удвоенную частоту и располагается симметрично относительно оси времени.

3. Мгновенная мощность и энергетические процессы

Энергетические процессы в индуктивности имеют колебательный характер. Мгновенная мощность \( p(t) \) определяется произведением мгновенных значений напряжения и тока:

p(t) = u(t) \cdot i(t) = U_m \sin(\omega t + \psi_u) \cdot I_m \sin(\omega t + \psi_i)

Используя тригонометрические преобразования и учитывая, что \( \psi_u = \psi_i + \frac{\pi}{2} \), получаем:

p(t) = U I \sin(2(\omega t + \psi_i))

Где \( U \) и \( I \) — действующие значения напряжения и тока (\( U = U_m / \sqrt{2} \), \( I = I_m / \sqrt{2} \)).

Особенности мощности в индуктивности:

Удвоенная частота: Мощность изменяется с частотой \( 2\omega \).
Колебательный характер: В одну четверть периода (когда \( p > 0 \)) энергия забирается от источника и запасается в магнитном поле катушки. В следующую четверть (когда \( p < 0 \)) энергия магнитного поля возвращается обратно в источник.
Активная мощность равна нулю: \( P = 0 \). Поскольку за период среднее значение синусоиды равно нулю, индуктивность не потребляет энергию безвозвратно (не греется), а лишь обменивается ею с сетью.

Энергия магнитного поля \( W_м(t) \) также пульсирует с удвоенной частотой, так как связана с мощностью соотношением \( p(t) = \frac{dW_м}{dt} \).

Описание Рис. 2: Вектор тока \( \dot{I} \) отложен горизонтально (для примера). Вектор напряжения \( \dot{U}_L \) повернут относительно вектора тока на \( 90^\circ \) против часовой стрелки, что демонстрирует опережение напряжения.

4. Сравнение параметров элементов цепи

Для лучшего понимания места индуктивности в теории цепей, сравним её с резистором и конденсатором.

Параметр	Резистор (R)	Индуктивность (L)	Конденсатор (C)
Связь U и I	\( U = I \cdot R \) (Закон Ома)	\( U = L \frac{di}{dt} \)	\( I = C \frac{du}{dt} \)
Сдвиг фаз (\( \phi \))	\( 0^\circ \) (в фазе)	\( +90^\circ \) (U опережает I)	\( -90^\circ \) (U отстает от I)
Реактивное сопротивление	0	\( X_L = \omega L \)	\( X_C = \frac{1}{\omega C} \)
Активная мощность	\( P = I^2 R \) (тепло)	0	0
Энергия	Рассеивается	Магнитное поле (\( LI^2/2 \))	Электрическое поле (\( CU^2/2 \))

5. Преимущества и недостатки модели «Идеальная индуктивность»

Применение идеализированной модели имеет свои плюсы и минусы в инженерных расчетах.

Преимущества:

Упрощает математический аппарат (дифференциальные уравнения становятся линейными).
Позволяет легко оценить реактивную мощность и фазовые сдвиги.
Достаточна для расчетов силовых трансформаторов и реакторов с высокой добротностью.

Недостатки:

Не учитывает активное сопротивление провода (R), которое есть у любой реальной катушки.
Игнорирует межвитковую емкость, которая становится критичной на высоких частотах (может возникнуть паразитный резонанс).
Не учитывает потери в сердечнике (гистерезис, вихревые токи).

6. Интересные факты

ИНЕРЦИЯ ЭЛЕКТРИЧЕСТВА Индуктивность часто называют «электрической инерцией». Подобно тому, как масса тела мешает мгновенно изменить его скорость, индуктивность мешает мгновенно изменить силу тока.
МНЕМОНИЧЕСКОЕ ПРАВИЛО В англоязычной литературе используется фраза «ELI the ICE man», где ELI означает: E (напряжение) опережает I (ток) в L (индуктивности).
ОПАСНОСТЬ РАЗРЫВА Попытка мгновенно разорвать цепь с большой индуктивностью приводит к теоретически бесконечному скачку напряжения. На практике это вызывает электрическую дугу на контактах выключателя.
СВЕРХПРОВОДНИКИ В сверхпроводящих катушках активное сопротивление действительно равно нулю. Ток, запущенный в такое кольцо, может циркулировать годами без затухания.
ЗАВИСИМОСТЬ ОТ ЧАСТОТЫ Для постоянного тока (\( \omega = 0 \)) индуктивное сопротивление равно нулю. Катушка ведет себя как обычный проводник (короткое замыкание для идеальной модели).
РЕАКТИВНАЯ МОЩНОСТЬ Хотя индуктивность не потребляет активную энергию, она «загружает» линии электропередач реактивным током, что требует увеличения сечения проводов.
ИЗМЕРИТЕЛЬНЫЙ ПАРАДОКС Обычный бытовой счетчик электроэнергии не будет «крутиться», если подключить к нему идеальную индуктивность, даже если ток в цепи огромен.

7. FAQ: Часто задаваемые вопросы

1. Почему напряжение опережает ток именно на 90 градусов?

Это математическое следствие производной синуса. Физически это объясняется тем, что ЭДС самоиндукции максимальна тогда, когда скорость изменения тока максимальна. У синусоиды тока максимальная скорость изменения (крутизна графика) наблюдается в момент перехода через ноль. Именно в этот момент напряжение достигает максимума.

2. Что будет, если подать постоянный ток на идеальную катушку?

Поскольку частота \( \omega = 0 \), индуктивное сопротивление \( X_L = 0 \). Идеальная катушка станет коротким замыканием. В реальной жизни ток будет ограничен только активным сопротивлением провода, что может привести к перегоранию.

3. В чем измеряется реактивная мощность Q?

Реактивная мощность измеряется в вольт-амперах реактивных (вар, var), чтобы отличать её от активной мощности (ватт) и полной мощности (вольт-ампер).

4. Влияет ли материал сердечника на \( L \)?

Да, кардинально. Введение ферромагнитного сердечника (железо, феррит) увеличивает индуктивность \( L \) в тысячи раз благодаря магнитной проницаемости \( \mu \).

5. Что такое добротность катушки?

Это отношение реактивного сопротивления к активному (\( Q = \omega L / R \)). Чем выше добротность, тем ближе реальная катушка к идеальной модели, рассмотренной в этой статье.

Заключение

Рассмотрение синусоидального тока в идеальном индуктивном элементе является базовым этапом в изучении электротехники. Понимание того, как связаны ток, напряжение и магнитное поле, позволяет переходить к анализу более сложных RLC-цепей, резонансных явлений и работе трансформаторов. Несмотря на абстрактность понятия «идеальный элемент», эта модель с высокой точностью описывает процессы в мощных электрических машинах и высокочастотных компонентах.

Нормативная база и литература

При проектировании и анализе индуктивных элементов необходимо руководствоваться следующими стандартами:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». (Определяет понятия индуктивности, реактивного сопротивления).
ГОСТ 2.723-68 «Единая система конструкторской документации. Обозначения условные графические в схемах. Катушки индуктивности, дроссели, трансформаторы».
ГОСТ 19880-74 «Электротехника. Основные понятия. Термины и определения».

Список литературы:

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2020.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — Л.: Энергоиздат, 1981.