Комплексные числа в электротехнике: Теория, формулы и расчеты

Содержание страницы

1. Алгебраическая, показательная, полярная и тригонометрическая формы
2. Представление синусоидальных функций комплексными числами
3. Математические операции и законы цепей
4. Сравнительная таблица форм записи
5. Практические примеры с решениями
6. Интересные факты о комплексных числах в электротехнике
7. FAQ: Часто задаваемые вопросы
Заключение

Что это и зачем нужно? Символический метод (или метод комплексных амплитуд) — это мощнейший математический инструмент, который превращает сложные дифференциальные уравнения электрических цепей в простые алгебраические задачи. Суть метода заключается в замене синусоидальных функций времени (токов и напряжений) неподвижными векторами на комплексной плоскости. Это позволяет использовать законы Ома и Кирхгофа для цепей переменного тока так же легко, как и для постоянного.

Историческая справка: Метод был предложен выдающимся инженером и математиком Чарльзом Протеусом Штейнмецем (Charles Proteus Steinmetz) в 1893 году. Его доклад на Международном электрическом конгрессе совершил революцию в электротехнике, позволив инженерам быстро рассчитывать сложные системы переменного тока, которые ранее требовали громоздких вычислений.

1. Алгебраическая, показательная, полярная и тригонометрическая формы

Трудности расчета цепей синусоидального тока значительно облегчает применение символического метода. Он основан на замене операций с синусоидальными функциями времени операциями с комплексными числами. Именно поэтому символический метод часто называют комплексным методом.

Ранее в курсе теоретических основ электротехники (ТОЭ) рассматривались векторные диаграммы напряжений и токов. Они базируются на представлении синусоидальных функций с помощью вращающихся векторов на декартовой плоскости $x0y$. Однако векторы можно изображать не только в декартовой системе, но и на комплексной плоскости в виде комплексных чисел.

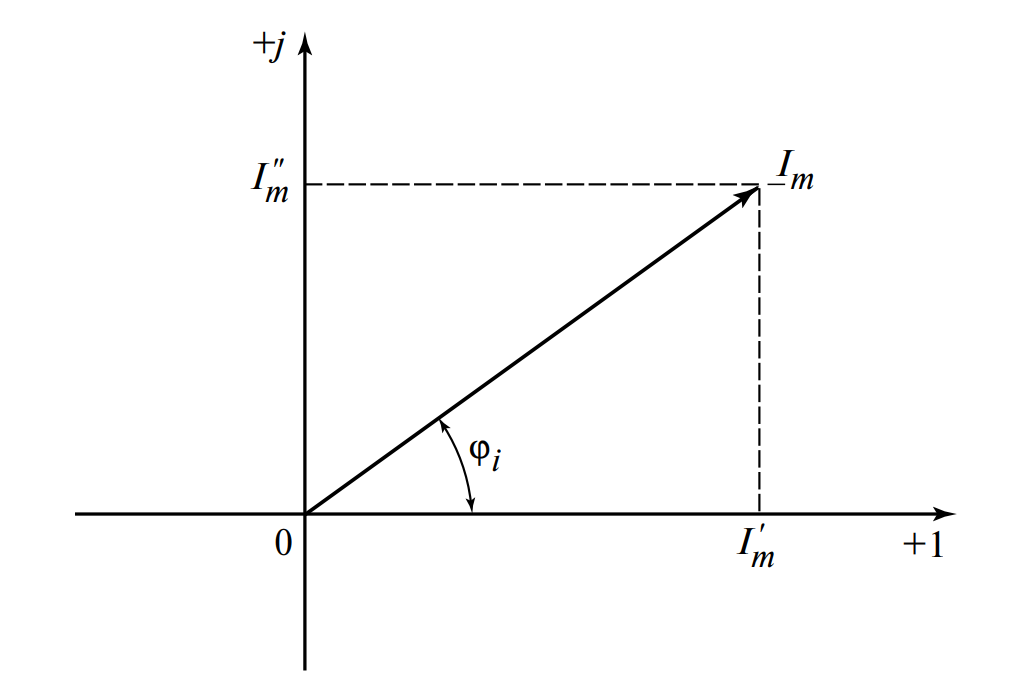
На рисунке изображена система координат: горизонтальная ось обозначена «+1» и «–1», вертикальная ось обозначена «+j» и «–j». Из начала координат выходит вектор, обозначенный как $\underline{I}_m$. Конец вектора имеет проекцию на горизонтальную ось $I’_m$ и на вертикальную ось $I»_m$. Угол между вектором и положительной вещественной полуосью обозначен $\psi_i$. Длина вектора обозначена $I_m$.

Рис. 1. Изображение комплексного числа на комплексной плоскости

Как показано на рис. 1, комплексное число состоит из двух частей:

Вещественная (действительная) часть: откладывается по оси абсцисс. Ось обозначают $+1$ и $-1$.
Мнимая часть: откладывается по оси ординат. Ось обозначают $+j$ и $-j$.

Важно! В электротехнике мнимая единица обозначается буквой $j$, чтобы не путать её с символом мгновенного значения тока $i$.

j = \sqrt{-1}

Комплексные амплитуды токов обозначаются прописной буквой с точкой или чертой снизу: $\underline{I}_m$. Для гармонических функций допускается обозначение точкой сверху $\dot{I}_m$. Комплексное число изображается вектором, соединяющим начало координат и точку на плоскости.

Алгебраическая форма

Координаты конца вектора определяются его проекциями:

Действительная составляющая: $I’_m = \text{Re}\{\underline{I}_m\}$.
Мнимая составляющая: $I»_m = \text{Im}\{\underline{I}_m\}$.

Запись в виде суммы этих составляющих называется алгебраической формой:

\underline{I}_m = I’_m + jI»_m

Тригонометрическая и полярная формы

Комплексное число также можно представить в полярной системе координат. Вектор характеризуется:

Модулем $I_m$ (длина вектора).
Аргументом $\psi_i$ (угол с полярной осью $+1$).

Связь между координатами и параметрами вектора очевидна из прямоугольного треугольника на рис. 1:

I’_m = I_m \cos \psi_i $$ $$ I»_m = I_m \sin \psi_i

Отсюда получаем тригонометрическую форму записи:

\underline{I}_m = I_m (\cos \psi_i + j \sin \psi_i)

Показательная форма

Используя знаменитую формулу Эйлера $e^{j\psi} = \cos \psi + j \sin \psi$, мы приходим к наиболее компактной, показательной форме:

\underline{I}_m = I_m e^{j\psi_i}

Иногда используют сокращенную полярную запись (с символом угла):

\underline{I}_m = I_m \angle \psi_i

Модуль и аргумент рассчитываются через алгебраические составляющие:

I_m = \sqrt{(I’_m)^2 + (I»_m)^2} $$ $$ \psi_i = \arctan \left( \frac{I»_m}{I’_m} \right)

2. Представление синусоидальных функций комплексными числами

Представим себе, что вектор $\underline{I}_m$ вращается на комплексной плоскости вокруг точки $0$ с угловой частотой $\omega$ против часовой стрелки (рис. 2).

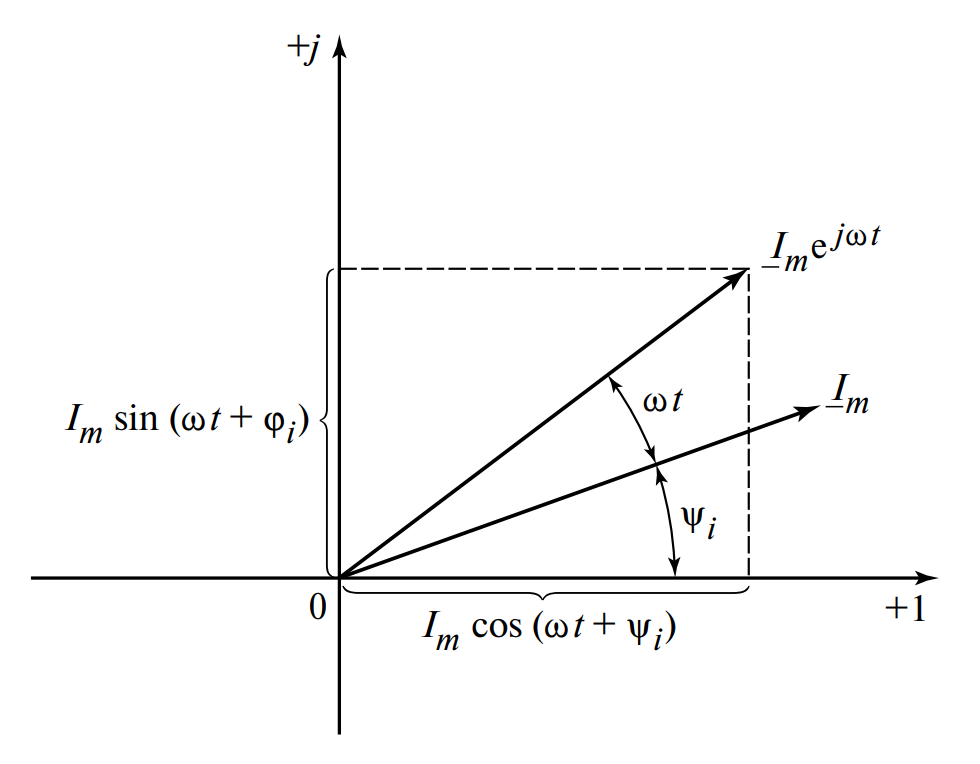
На рисунке показана комплексная плоскость с осями +1 и +j. Вектор длиной $I_m$ повернут на угол $\omega t + \psi_i$ относительно действительной оси. Проекция вектора на мнимую ось обозначена как $I_m \sin(\omega t + \psi_i)$, проекция на действительную ось — $I_m \cos(\omega t + \psi_i)$. Сам вектор обозначен как $\underline{I}_m e^{j\omega t}$.

Рис. 2. Представление синусоиды с помощью комплексной функции

Аналогия для понимания: Представьте стрелку часов, вращающуюся против обычного хода. Если мы посветим на эти часы фонариком сбоку, тень от стрелки на стене будет то удлиняться, то укорачиваться, совершая колебательные движения. Эта тень — и есть наша синусоида (или косинусоида), а стрелка — это вращающийся комплексный вектор.

Математически такому вращающемуся вектору соответствует комплексная функция времени:

\underline{I}(t) = \underline{I}_m e^{j\omega t} = I_m e^{j(\omega t + \psi_i)}

В произвольный момент времени $t$ этот вектор образует с действительной осью угол $\omega t + \psi_i$. Его проекции равны:

\text{Re}\{\underline{I}_m e^{j\omega t}\} = I_m \cos (\omega t + \psi_i) $$ $$ \text{Im}\{\underline{I}_m e^{j\omega t}\} = I_m \sin (\omega t + \psi_i)

Как видно, мнимая часть этой комплексной функции описывает синусоидальный ток:

i(t) = I_m \sin (\omega t + \psi_i)

Следует отметить важное различие в традициях:

В энергетике и электротехнике гармонические функции обычно описываются через синусы (мнимая часть комплексной функции).
В радиоэлектронике и теории связи — через косинусы (действительная часть).

Если представить, что сама комплексная плоскость вращается вместе с вектором с частотой $\omega$ против часовой стрелки, то вектор $\underline{I}_m = I_m \angle \psi_i$ будет казаться неподвижным. Это обстоятельство — ключ к методу. Оно позволяет утверждать, что синусоидальная функция может быть представлена неподвижным комплексным числом. Работать с числами (пусть и комплексными) гораздо проще, чем с громоздкими тригонометрическими функциями.

3. Математические операции и законы цепей

Представление синусоидальных токов, напряжений и ЭДС комплексными числами позволяет рассчитывать цепи переменного тока методами, аналогичными методам цепей постоянного тока (DC).

Законы Ома и Кирхгофа в комплексной форме

В уравнениях по первому и второму законам Кирхгофа мгновенные значения $i, u, e$ заменяются на комплексные:

Комплексные амплитуды: $\underline{I}_m, \underline{U}_m, \underline{E}_m$.
Или комплексные действующие значения: $\underline{I}, \underline{U}, \underline{E}$.

Соотношение между амплитудными и действующими значениями в комплексной области сохраняется (для синусоиды делим на $\sqrt{2}$):

\underline{I} = \frac{\underline{I}_m}{\sqrt{2}}; \quad \underline{U} = \frac{\underline{U}_m}{\sqrt{2}}; \quad \underline{E} = \frac{\underline{E}_m}{\sqrt{2}}

Важное условие: Комплексный метод используется для расчета токов и напряжений одной и той же частоты.

Операции с комплексными числами

Разные формы записи удобны для разных арифметических действий.

Сложение и вычитание

Удобнее производить в алгебраической форме. Пусть даны два числа $\underline{A} = A’ + jA»$ и $\underline{B} = B’ + jB»$:

\underline{A} \pm \underline{B} = (A’ \pm B’) + j(A» \pm B»)

Умножение и деление

Значительно легче выполнять в показательной (или полярной) форме. Пусть $\underline{A} = A \angle \alpha$ и $\underline{B} = B \angle \beta$:

\underline{A} \cdot \underline{B} = (A \cdot B) \angle (\alpha + \beta) $$ $$ \frac{\underline{A}}{\underline{B}} = \frac{A}{B} \angle (\alpha — \beta)

Однако можно умножать и делить и в алгебраической форме, раскрывая скобки как в обычных двучленах и помня, что $j^2 = -1$:

\underline{A} \cdot \underline{B} = (A’ + jA»)(B’ + jB») = (A’B’ — A»B») + j(A»B’ + A’B»)

Для деления в алгебраической форме числитель и знаменатель домножают на число, сопряженное знаменателю.

Комплексно-сопряженные числа: Числа с одинаковыми действительными частями и противоположными по знаку мнимыми называются сопряженными (например, $B’ + jB»$ и $B’ — jB»$).
Их произведение всегда дает действительное число:
$$ (B’ + jB»)(B’ — jB») = (B’)^2 + (B»)^2 $$

4. Сравнительная таблица форм записи

Для наглядности сведем все формы записи в одну таблицу, чтобы вы могли выбрать наиболее удобную для конкретной задачи.

Форма записи	Общий вид	Для чего удобна	Недостатки
Алгебраическая	$ \underline{Z} = a + jb $	Сложение и вычитание (законы Кирхгофа)	Неудобно умножать, делить, возводить в степень
Тригонометрическая	$ r(\cos\psi + j\sin\psi) $	Переход от полярной к алгебраической, визуализация	Громоздкая запись
Показательная (экспоненциальная)	$ r e^{j\psi} $	Умножение, деление, дифференцирование, интегрирование	Неудобна для сложения
Полярная	$ r \angle \psi $	Быстрая запись ответов, показания приборов	Нестандартная математическая запись (инженерный сленг)

5. Практические примеры с решениями

Ниже приведены решения задач. Проверьте свои вычисления.

Задача 1. Найти модуль и аргумент

Перевод из алгебраической формы $ \underline{Z} = a + jb $ в полярную $ \underline{Z} = r \angle \psi $.
Формулы: $ r = \sqrt{a^2 + b^2} $, $ \psi = \text{arctg}(b/a) $ (с учетом четверти координатной плоскости).

$ 60 + j80 $
Решение: $ r = \sqrt{60^2 + 80^2} = 100 $; $ \psi = \text{arctg}(80/60) \approx 53,1^\circ $
Ответ: $ 100 \angle 53,1^\circ $
$ 80 — j60 $
Решение: $ r = \sqrt{80^2 + (-60)^2} = 100 $; $ \psi = \text{arctg}(-60/80) \approx -36,9^\circ $
Ответ: $ 100 \angle -36,9^\circ $
$ -300 — j100 $ (III четверть)
Решение: $ r = \sqrt{(-300)^2 + (-100)^2} \approx 316,2 $; $ \psi = \text{arctg}(\frac{-100}{-300}) — 180^\circ \approx -161,6^\circ $
Ответ: $ 316,2 \angle -161,6^\circ $
$ -20 + j70 $ (II четверть)
Решение: $ r = \sqrt{(-20)^2 + 70^2} \approx 72,8 $; $ \psi = \text{arctg}(\frac{70}{-20}) + 180^\circ \approx 105,9^\circ $
Ответ: $ 72,8 \angle 105,9^\circ $
$ 9 — j0,5 $
Решение: $ r = \sqrt{9^2 + (-0,5)^2} \approx 9,01 $; $ \psi = \text{arctg}(-0,5/9) \approx -3,2^\circ $
Ответ: $ 9,01 \angle -3,2^\circ $
$ -0,003 + j0,0002 $ (II четверть)
Решение: $ r \approx 0,003 $; $ \psi \approx 176,2^\circ $
Ответ: $ 0,003 \angle 176,2^\circ $

Задача 2. Разложить на составляющие

Перевод из полярной формы $ r \angle \psi $ в алгебраическую $ a + jb $.
Формулы: $ a = r \cos \psi $, $ b = r \sin \psi $.

$ 5 \angle 30^\circ $
Ответ: $ 4,33 + j2,5 $
$ 10 \angle 70^\circ $
Ответ: $ 3,42 + j9,40 $
$ 0,2 \angle 100^\circ $
Ответ: $ -0,035 + j0,197 $
$ 0,035 \angle 170^\circ $
Ответ: $ -0,034 + j0,006 $
$ 250 \angle 195^\circ $
Ответ: $ -241,48 — j64,70 $
$ 30 \angle -112^\circ $
Ответ: $ -11,24 — j27,82 $
$ 2 \angle 275^\circ $ (или $ -85^\circ $)
Ответ: $ 0,17 — j1,99 $
$ 380 \angle -30^\circ $
Ответ: $ 329,09 — j190 $
$ 0,017 \angle 269^\circ $ (почти мнимая ось вниз)
Ответ: $ 0,0003 — j0,017 $
$ 1000 \angle -178^\circ $
Ответ: $ -999,39 — j34,90 $
$ -15 \angle 40^\circ $ (отрицательный модуль разворачивает вектор)
Решение: $ -15(\cos 40^\circ + j\sin 40^\circ) $
Ответ: $ -11,49 — j9,64 $

6. Интересные факты о комплексных числах в электротехнике

Обозначение j. Буква $i$ была «занята» током (intensity of current), поэтому инженеры взяли соседнюю букву $j$ для мнимой единицы.
История внедрения. Оливер Хевисайд и Чарльз Штейнмец встретили сопротивление научного сообщества, когда внедряли этот метод. Многим он казался «слишком абстрактным» и оторванным от реальности.
Термин «фазор». Phasor — это вектор на комплексной плоскости, представляющий гармоническую функцию. Это слияние англ. слов phase vector («фазовый вектор»).
Комплексная мощность. Полная мощность в цепи переменного тока $S$ — это тоже комплексное число: $S = P + jQ$, где $P$ — активная (греющая), а $Q$ — реактивная (колеблющаяся) мощность.
Оператор «a». В трехфазных сетях для упрощения записей оператор поворота на 120 градусов обозначается буквой $a$ и равен $e^{j120^\circ}$.
Импеданс vs Фазор. Импеданс (полное сопротивление) $\underline{Z} = R + jX$ не является фазором, так как он не вращается во времени, хотя и записывается как комплексное число. Это параметр цепи, а не функция времени.
Масштаб применения. Без символического метода расчет режимов современной Единой энергосистемы был бы невозможен — дифференциальные уравнения были бы нерешаемыми за разумное время.

7. FAQ: Часто задаваемые вопросы

Вопрос 1: Какой физический смысл у мнимой части тока?

В реальности тока «мнимого» не существует. Мнимая часть в расчетах показывает фазовый сдвиг компоненты тока на 90 градусов относительно выбранной базы. Вместе действительная и мнимая части описывают реальную синусоиду.

Вопрос 2: Можно ли использовать градусы в показательной форме?

В строгой математике в показателе степени экспоненты $e^{j\dots}$ должны стоять радианы. Однако в инженерной практике часто пишут градусы для наглядности, подразумевая перевод: $e^{j90^\circ}$.

Вопрос 3: Почему метод работает только для одной частоты?

Потому что реактивные сопротивления (катушек $X_L = \omega L$ и конденсаторов $X_C = 1/\omega C$) зависят от частоты $\omega$. Если частоты разные, параметры цепи меняются, и принцип суперпозиции требует расчета для каждой частоты отдельно.

Вопрос 4: Что делать, если у меня на калькуляторе нет комплексных чисел?

Для обучения придется считать вручную через формулы перехода (корень из суммы квадратов и арктангенс). Для работы лучше скачать инженерный калькулятор или использовать Python/Matlab.

Вопрос 5: Где применяется этот метод кроме электрики?

Везде, где есть колебания: акустика, квантовая механика, теория упругости, обработка сигналов, аэродинамика.

Заключение

Символический метод является фундаментом современной электротехники. Замена дифференцирования и интегрирования синусоид на алгебраические операции с комплексными числами позволяет инженерам эффективно проектировать и анализировать цепи любой сложности. Понимание форм записи (алгебраической, тригонометрической и показательной) — первый и самый важный шаг к мастерству в ТОЭ.

Нормативная база и литература

При оформлении технической документации и схем следует руководствоваться действующими стандартами:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». (Действующий). Определяет основные термины, включая комплексные величины.
ГОСТ 2.701-2008 «ЕСКД. Схемы. Виды и типы. Общие требования к выполнению».
Бессонов Л.А. «Теоретические основы электротехники. Электрические цепи». Классический учебник для ВУЗов.
Нейман Л.Р., Демирчян К.С. «Теоретические основы электротехники».