Резонансные режимы и частотные характеристики цепей RLC

Содержание страницы

1. Резонанс токов (параллельный резонанс)
2. Резонанс напряжений (последовательный резонанс)
3. Частотные характеристики и избирательность
4. Сравнительный анализ резонансных режимов
5. Преимущества и недостатки использования резонанса
6. Интересные факты о резонансе
7. Часто задаваемые вопросы (FAQ)
Заключение

Явление резонанса в электрических цепях представляет собой фундаментальный физический процесс, при котором пассивная электрическая цепь, содержащая ёмкостные и индуктивные элементы, ведет себя как чисто активная нагрузка при определенной частоте внешнего воздействия. В этом состоянии наблюдается взаимная компенсация реактивных мощностей, что приводит к экстремальным значениям токов или напряжений на отдельных участках цепи.

Исторически изучение резонансных явлений началось задолго до появления электротехники, в механике и акустике (работы Галилея). В электромагнетизме ключевую роль сыграли эксперименты Генриха Герца (1887 г.) с вибратором, подтвердившие теорию Максвелла, где резонанс использовался для генерации и детектирования электромагнитных волн. Понимание резонанса критически важно как для задач передачи энергии (где его стараются избегать или контролировать), так и для радиотехники и связи (где на нем основана вся селекция сигналов).

В электрической цепи, содержащей разнородные реактивные элементы (индуктивности $L$ и ёмкости $C$), возможны особые режимы работы, когда вектор общего напряжения и вектор общего тока на входе цепи совпадают по фазе. В таком режиме входное сопротивление (или проводимость) цепи становится чисто активным, а суммарная реактивная мощность, потребляемая от источника, равна нулю. Вся энергия, поступающая от источника, расходуется только на активных сопротивлениях.

Рассмотрим детально два основных вида резонансных режимов, их условия возникновения, векторные диаграммы и практическое применение, а также проанализируем частотные характеристики таких цепей.

1. Резонанс токов (параллельный резонанс)

Резонанс токов возникает в электрической цепи, образованной параллельным соединением ветвей, содержащих разнородные реактивные элементы. Классическим примером является цепь с двумя параллельными ветвями: одна содержит индуктивность, другая — ёмкость.

Условием возникновения резонанса токов является равенство реактивных проводимостей этих параллельных ветвей:
$$ b_L = b_C $$
где $b_L$ — индуктивная проводимость, $b_C$ — ёмкостная проводимость.

В общем случае, если ветви содержат также активные сопротивления, полная проводимость цепи $Y$ определяется как:
$$ Y = \sqrt{g^2 + (b_L — b_C)^2} $$
где $g = g_1 + g_2$ — суммарная активная проводимость ветвей. При резонансе, когда $b_L — b_C = 0$, полная проводимость становится минимальной и равной чисто активной проводимости $Y_{min} = g$.

Суммарный ток в неразветвленной части цепи при этом достигает своего минимального значения и совпадает по фазе с приложенным напряжением:

$$ \dot{I} = \dot{I}_g + \dot{I}_L + \dot{I}_C = U(g + j(b_L — b_C)) $$

При резонансе ($b_L = b_C$) реактивная составляющая тока равна нулю, и выражение упрощается до:

$$ \dot{I} = U \cdot g = \dot{I}_a $$

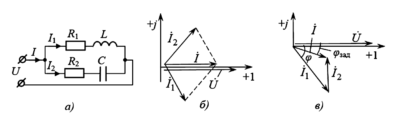
Рисунок 1. Резонанс токов: а — принципиальная схема цепи; б — векторная диаграмма при условии $b_L = b_C$; в — векторная диаграмма при компенсации индуктивной мощности батареей конденсаторов.

На Рисунке 1(б) показана векторная диаграмма при идеальном резонансе токов. Видно, что реактивные составляющие токов ветвей $\dot{I}_{L}$ и $\dot{I}_{C}$ равны по модулю и противоположны по фазе, компенсируя друг друга. Суммарный ток $\dot{I}$ совпадает с вектором напряжения $\dot{U}$.

Замечание: При малых активных проводимостях ветвей ($g_1, g_2 \to 0$) токи в реактивных элементах могут значительно (в $Q$ раз, где $Q$ — добротность контура) превышать общий ток, потребляемый от источника. Это явление потенциально опасно перегрузкой отдельных ветвей при кажущемся малом общем потреблении тока.

Проводимости ветвей при последовательном включении элементов внутри ветви (как на рис. 1а) рассчитываются по формулам:

$$ Y_1 = \frac{1}{Z_1} = \frac{1}{R_1 + jX_L} = \frac{R_1}{R_1^2 + X_L^2} — j\frac{X_L}{R_1^2 + X_L^2} = g_1 — jb_L $$
$$ Y_2 = \frac{1}{Z_2} = \frac{1}{R_2 — jX_C} = \frac{R_2}{R_2^2 + X_C^2} + j\frac{X_C}{R_2^2 + X_C^2} = g_2 + jb_C $$

Условие резонанса $b_1 = b_2$ в развернутом виде:

$$ \frac{X_L}{R_1^2 + X_L^2} = \frac{X_C}{R_2^2 + X_C^2} $$

Практическое применение: Компенсация реактивной мощности

Явление, аналогичное резонансу токов, широко используется в промышленном электроснабжении. Большинство промышленных потребителей (асинхронные двигатели, трансформаторы) представляют собой активно-индуктивную нагрузку. Это приводит к потреблению значительной реактивной мощности из сети, увеличению общего тока и потерям в линиях электропередачи.

Подключение батареи статических конденсаторов (БСК) параллельно такой нагрузке позволяет локально «генерировать» реактивную ёмкостную мощность, которая компенсирует индуктивную мощность потребителей. Это не обязательно полный резонанс, но приближение к нему.

На Рисунке 1(в) показана такая ситуация. Исходный ток цеха $\dot{I}_1$ отставал от напряжения на угол $\varphi$. После подключения конденсатора суммарный ток $\dot{I}$ уменьшился, а угол сдвига фаз снизился до $\varphi_{зад}$. Обычно стремятся достичь коэффициента мощности $\cos\varphi \approx 0,9…0,95$, избегая полной компенсации («перекомпенсации») во избежание неустойчивости режима при колебаниях нагрузки.

Пример расчета компенсации (Пример 1)

Дано: Активная мощность цеха $P = 200$ кВт. Напряжение сети $U = 380$ В. Потребляемый ток $I_1 = 1000$ А. Требуется определить ёмкость батареи конденсаторов для повышения коэффициента мощности до $\cos\varphi_{зад} = 0,9$.

Решение:

Определим исходный коэффициент мощности и угол сдвига фаз:
$$ \cos\varphi_1 = \frac{P}{U \cdot I_1} = \frac{200000}{380 \cdot 1000} \approx 0,526 $$
$$ \varphi_1 = \arccos(0,526) \approx 58,2^\circ $$
Определим исходную реактивную мощность:
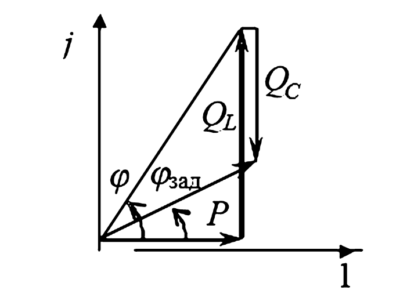
$$ Q_L = P \cdot \ tan \varphi_1 = 200 \cdot \ tan (58,2^\circ) \approx 322 \text{ квар} $$
Требуемая реактивная мощность после компенсации:
$$ Q_{рез} = P \cdot \ tan (\arccos 0,9) = 200 \cdot 0,484 \approx 96,8 \text{ квар} $$
Необходимая мощность конденсаторной батареи $Q_C$:
$$ Q_C = Q_L — Q_{рез} = P(\ tan \varphi_1 — \ tan \varphi_{зад}) = 322 — 96,8 = 225,2 \approx 226 \text{ квар} $$

Рисунок 2. Треугольник мощностей для расчета компенсации реактивной мощности.

Ёмкость батареи $C$ определяется из формулы реактивной мощности:
$$ Q_C = U^2 \cdot \omega C \implies C = \frac{Q_C}{\omega U^2} $$
При стандартной частоте 50 Гц ($\omega \approx 314$ рад/с):
$$ C = \frac{226000}{314 \cdot 380^2} \approx 0,005 \text{ Ф} = 5000 \text{ мкФ} $$

2. Резонанс напряжений (последовательный резонанс)

Резонанс напряжений возникает в последовательной RLC-цепи (Рисунок 3а). В этом режиме реактивные сопротивления индуктивности и ёмкости становятся равными по модулю:

$$ X_L = X_C \implies \omega L = \frac{1}{\omega C} $$

Частота, при которой выполняется это условие, называется резонансной частотой $\omega_0$:

$$ \omega_0 = \frac{1}{\sqrt{LC}} $$

В режиме резонанса напряжений полное сопротивление цепи $Z$ становится минимальным и чисто активным:
$$ Z = \sqrt{R^2 + (X_L — X_C)^2} = R $$
Следовательно, ток в цепи достигает своего максимума:
$$ I_0 = \frac{U}{R} $$

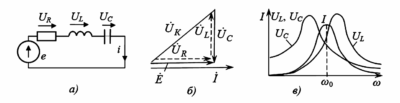
Рисунок 3. Резонанс напряжений: а — схема цепи; б — векторная диаграмма; в — резонансные кривые зависимости тока и напряжений от частоты.

Векторная диаграмма (Рисунок 3б) показывает, что напряжения на индуктивности $\dot{U}_L$ и ёмкости $\dot{U}_C$ равны по амплитуде и находятся в противофазе, взаимно компенсируя друг друга. Напряжение источника полностью приложено к активному сопротивлению $R$.

Критически важным параметром является добротность контура $Q$. Она показывает, во сколько раз напряжения на реактивных элементах при резонансе могут превышать напряжение источника:

$$ Q = \frac{U_{L0}}{U} = \frac{U_{C0}}{U} = \frac{I_0 \cdot \omega_0 L}{I_0 R} = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 C R} = \frac{\rho}{R} $$
где $\rho = \sqrt{L/C}$ — характеристическое (волновое) сопротивление контура.

Опасность резонанса напряжений: В высоковольтных цепях с малой активной составляющей $R$ (высокой добротностью) случайное возникновение резонанса может привести к катастрофическим последствиям. Напряжения на катушках и конденсаторах могут в десятки раз превысить номинальное напряжение сети, вызывая пробой изоляции и аварии.

3. Частотные характеристики и избирательность

Для анализа поведения цепей в широком диапазоне частот применяют комплексные частотные характеристики (КЧХ). КЧХ — это отношение комплексного отклика цепи к комплексному гармоническому воздействию в зависимости от частоты:

$$ H(j\omega) = \frac{\dot{Y}_{вых}(j\omega)}{\dot{X}_{вх}(j\omega)} = |H(\omega)| e^{j\psi(\omega)} $$

Различают две основные составляющие КЧХ:

Амплитудно-частотная характеристика (АЧХ): $ |H(\omega)| $ — зависимость модуля коэффициента передачи от частоты.
Фазо-частотная характеристика (ФЧХ): $ \psi(\omega) $ — зависимость фазового сдвига между выходом и входом от частоты.

Электрические резонансные цепи обладают свойством избирательности — способностью выделять сигналы определенных частот из спектра и подавлять остальные. Это свойство лежит в основе всей радиоприемной техники.

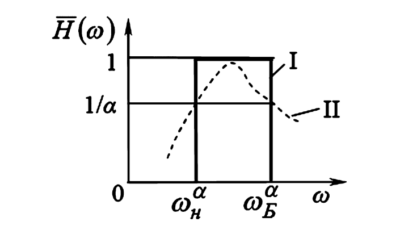
Рисунок 4. Нормированная АЧХ избирательной цепи: I — идеальная; II — реальная.

Для последовательного колебательного контура (ПСК) в качестве КЧХ часто рассматривают его входную проводимость. Однако более наглядна нормированная характеристика тока, которая совпадает по форме с АЧХ проводимости.

Для унификации анализа вводят понятие обобщенной расстройки $\xi$:

$$ \xi = Q \left( \frac{\omega}{\omega_0} — \frac{\omega_0}{\omega} \right) \approx \frac{2Q \Delta\omega}{\omega_0} $$
где $\Delta\omega = \omega — \omega_0$ — абсолютная расстройка (справедливо вблизи резонанса).

Нормированная АЧХ последовательного контура описывается универсальным уравнением:

$$ A(\xi) = \frac{I}{I_0} = \frac{1}{\sqrt{1 + \xi^2}} $$
а нормированная ФЧХ:
$$ \psi(\xi) = -\arctan(\xi) $$

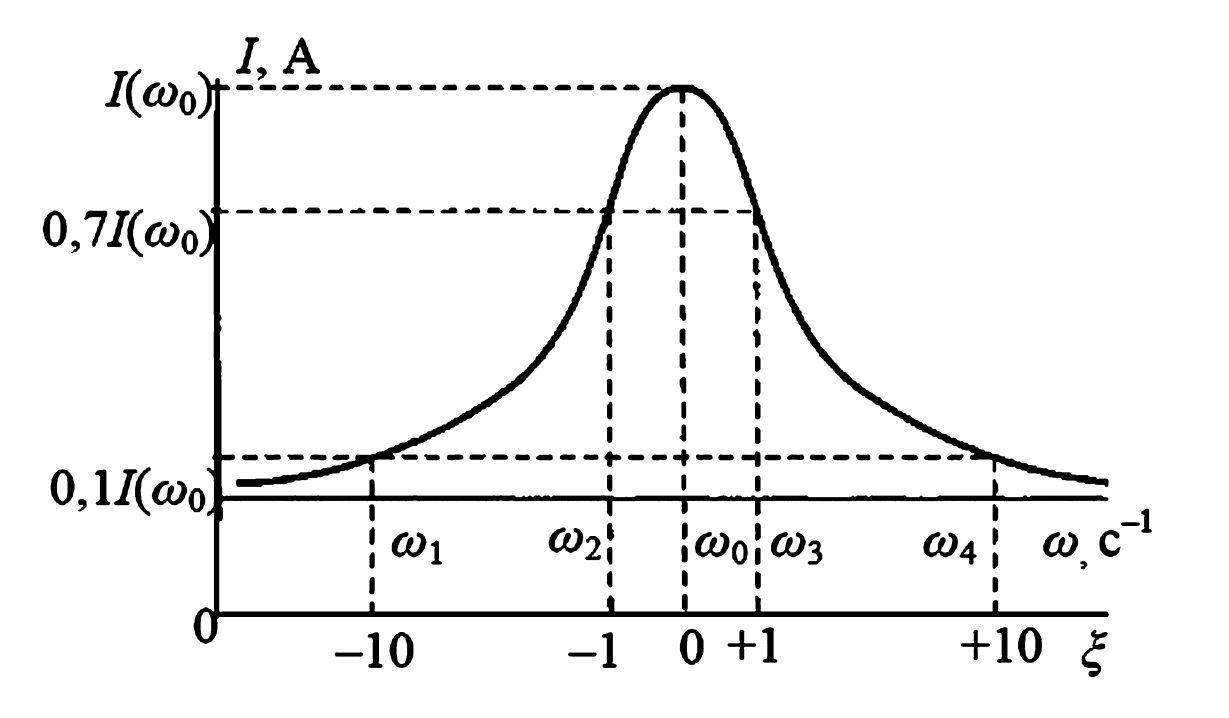
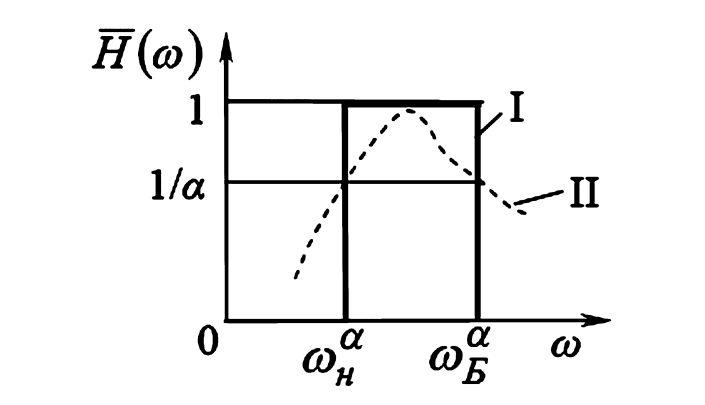
Рисунок 5. Входная резонансная характеристика последовательного колебательного контура.

Полоса пропускания ($\Delta\omega_{пр}$) определяется на уровне $1/\sqrt{2} \approx 0,707$ от максимального значения АЧХ. Этой полосе соответствует значение обобщенной расстройки $\xi = \pm 1$.
Ширина полосы пропускания связана с добротностью:

$$ \Delta\omega_{пр} = \frac{\omega_0}{Q} $$

Для оценки качества избирательности используют коэффициент прямоугольности $K_{пр}$, равный отношению полосы пропускания к полосе мешания (обычно на уровне 0,1):

$$ K_{пр} = \frac{\Delta\omega_{0.7}}{\Delta\omega_{0.1}} $$

Для одиночного колебательного контура этот коэффициент всегда равен приблизительно 0,1, что говорит о низкой селективности. Для улучшения избирательности применяют связанные контуры или специальные фильтры, где $K_{пр}$ может достигать значений 0,43 и выше, приближая форму АЧХ к идеальному прямоугольнику.

4. Сравнительный анализ резонансных режимов

Таблица 1. Сравнение последовательного и параллельного резонанса
Характеристика	Резонанс напряжений (Последовательный)	Резонанс токов (Параллельный)
Схема включения L и C	Последовательно	Параллельно
Условие резонанса	$X_L = X_C$	$b_L = b_C$ (или $X_L \approx X_C$ при малом R)
Полное сопротивление цепи (Z)	Минимальное ($Z_{min} = R$)	Максимальное ($Z_{max} = R_{экв}$)
Ток от источника	Максимальный ($I = U/R$)	Минимальный (в идеале 0)
Опасный фактор	Перенапряжение на L и C ($U_L, U_C \gg U_{вх}$)	Сверхтоки внутри контура ($I_L, I_C \gg I_{вх}$)
Основное применение	Входные цепи радиоприемников, фильтры	Заграждающие фильтры, компенсация реактивной мощности

5. Преимущества и недостатки использования резонанса

Преимущества

Высокая избирательность: Возможность выделения узкой полосы частот (полезного сигнала) из зашумленного спектра.
Коэффициент усиления напряжения: Пассивный RLC-контур может усиливать напряжение сигнала в $Q$ раз без использования активных усилительных элементов (транзисторов, ламп).
Энергоэффективность: Компенсация реактивной мощности в промышленных сетях снижает потери на нагрев проводов и разгружает трансформаторы.
Беспроводная передача энергии: Современные зарядные устройства используют резонансную индуктивную связь для повышения эффективности передачи.

Недостатки и опасности

Аварийные перенапряжения: В силовых сетях (6-35 кВ) непреднамеренный феррорезонанс трансформаторов напряжения с емкостью сети может привести к взрывам оборудования.
Перегрузки по току: Параллельный резонанс внутри фильтрокомпенсирующих устройств при неправильной настройке может вызвать термическое разрушение реакторов.
Нестабильность параметров: Высокодобротные контуры требуют точной настройки и чувствительны к температурному дрейфу номиналов компонентов.

6. Интересные факты о резонансе

Разрушение мостов: Хотя классический пример с мостом и солдатами часто преувеличен, резонанс механических конструкций под действием ветра (как в случае с Такомским мостом) имеет ту же физическую природу, что и электрический резонанс — совпадение частоты внешнего воздействия с собственной частотой системы.
Tesla Coil: Знаменитая катушка Теслы — это, по сути, высокодобротный резонансный трансформатор, работающий в режиме резонанса напряжений для генерации гигантских электрических разрядов.
RFID-метки: Пассивные метки в магазинах не имеют батареек. Они получают энергию от считывателя именно благодаря резонансу во встроенном LC-контуре, настроенном на частоту считывателя.
Взрыв конденсаторов: Если в сети много высших гармоник (от частотных преобразователей), конденсаторные батареи могут войти в резонанс на частоте одной из гармоник (например, 5-й или 7-й) и взорваться от перегрузки по току.
Кварцевый резонатор: Для получения сверхвысокой добротности (Q > 10000), недостижимой в обычных LC-контурах, используют механический резонанс кристалла кварца, который имеет электрический эквивалент последовательно-параллельного контура.
СВЧ-печи: Магнетрон генерирует волны, частота которых совпадает с резонансной частотой молекул воды, что и приводит к разогреву пищи. Это пример молекулярного резонанса.
Нулевой провод: В трехфазных сетях с нелинейной нагрузкой (компьютеры, LED-освещение) токи гармоник, кратных трем, суммируются в нулевом проводе, иногда вызывая его перегорание, даже если фазные нагрузки симметричны.

7. Часто задаваемые вопросы (FAQ)

Вопрос 1: Почему при резонансе токов общий ток минимален, а не максимален?

Потому что параллельный контур при резонансе имеет очень большое эквивалентное сопротивление. Токи ветвей (индуктивной и емкостной) находятся в противофазе и взаимно компенсируют друг друга во внешней цепи, замыкаясь внутри контура.

Вопрос 2: Что такое добротность простыми словами?

Добротность показывает, во сколько раз запасы энергии в контуре больше, чем потери энергии за один период колебаний. Чем выше добротность, тем «острее» резонансный пик и тем дольше затухают свободные колебания в контуре.

Вопрос 3: Можно ли получить резонанс в цепи без индуктивности или без емкости?

Нет, для электрического резонанса необходимы два типа накопителей энергии: электрического поля (емкость) и магнитного поля (индуктивность), между которыми происходит обмен энергией.

Вопрос 4: Как резонанс влияет на качество электроэнергии?

Неконтролируемый резонанс на частотах высших гармоник может существенно ухудшить качество электроэнергии, вызывая искажения синусоиды напряжения и перебои в работе чувствительного оборудования (согласно ГОСТ 32144-2013).

Вопрос 5: Зачем нужна расстройка контура?

Расстройка используется, когда нужно ослабить сигнал определенной частоты или для частотной модуляции/демодуляции сигналов.

Вопрос 6: Почему реальная резонансная частота отличается от формулы $\omega_0 = 1/\sqrt{LC}$?

Формула Томсона верна для идеального контура без потерь. В реальных цепях наличие активного сопротивления $R$ незначительно смещает резонансную частоту в сторону уменьшения.

Вопрос 7: Что такое «волновое сопротивление» контура?

Это характеристическое сопротивление $\rho = \sqrt{L/C}$, которое численно равно индуктивному (или емкостному) сопротивлению на резонансной частоте. Оно является важным параметром при согласовании контуров с линиями передачи.

Заключение

Понимание резонансных явлений является краеугольным камнем электротехники. От простейшего радиоприемника до гигантской энергосистемы — везде действуют одни и те же законы колебательных контуров. Грамотный инженер должен уметь не только рассчитывать параметры резонанса для полезного применения (фильтрация, компенсация реактивной мощности), но и предвидеть и предотвращать опасные резонансные режимы, способные привести к авариям.

Нормативная база и литература

ГОСТ IEC 60050-151-2014. Международный электротехнический словарь. Часть 151. Электрические и магнитные устройства. (Определения резонанса и связанных терминов).
ГОСТ 32144-2013. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения.
ГОСТ IEC 60831-1-2014. Конденсаторы шунтирующие силовые самовосстанавливающиеся для систем переменного тока на номинальное напряжение до 1000 В включительно.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2020.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — СПб.: Питер, 2019.