Компенсация реактивной мощности в сети: расчет, установки

Содержание страницы

1. Физика процесса: Визуализация сдвига фаз
2. Математическая модель: Треугольник мощностей
3. Две стороны коэффициента мощности: Displacement vs Distortion
4. Нормативное регулирование в РФ: Приказ № 380
5. Принцип компенсации: Векторная арифметика
6. Технологии компенсации: От Пассивных к Активным
7. Методика расчета компенсации
8. Интересные факты о реактивной мощности
9. Часто задаваемые вопросы (FAQ)
Заключение

В условиях ужесточения нормативной базы РФ (Приказ Минэнерго № 380) и роста стоимости технологического присоединения, игнорирование вопросов качества электроэнергии становится непозволительной роскошью. Данная статья представляет собой всестороннее техническое руководство по природе реактивной мощности, методам её расчета и современным стратегиям компенсации реактивной мощности.

Энергосистемы промышленных предприятий часто сталкиваются с парадоксом: потребление тока велико, кабели греются, трансформаторы работают на пределе, а полезная работа (вращение валов, нагрев печей) выполняется недостаточно эффективно. Виновником этого является реактивная мощность — «фантомная» энергия, которая циркулирует между источником и нагрузкой, не совершая необратимой работы.

Реактивная мощность — это один из самых сложных для понимания феноменов в электротехнике. Не совершая полезной работы, она загружает линии электропередач, вызывает перегрев изоляции и падение напряжения. Баланс между генерацией и потреблением этой энергии — ключ к энергоэффективности.

История этого понятия восходит к работам Чарльза Штейнмеца (1892 г.), который первым ввел комплексное представление мощности для анализа цепей переменного тока. Сегодня, спустя более 100 лет, с появлением нелинейных нагрузок (частотных приводов, LED-освещения), эта тема требует нового осмысления.

1. Физика процесса: Визуализация сдвига фаз

Чтобы понять природу реактивной мощности, необходимо взглянуть на осциллограммы напряжения $ U $ и тока $ I $. В идеальном мире эти синусоиды должны совпадать. Однако индуктивные нагрузки (двигатели) заставляют ток отставать от напряжения.

Рассмотрим три сценария, иллюстрирующие деградацию эффективности сети:

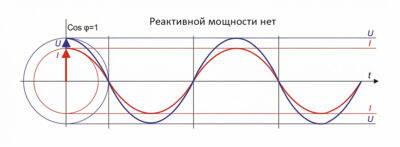
Осциллограмма тока, напряжения и реактивной мощности в сети при Cos Phi = 1

Вариант А: Идеал ($ \cos \varphi = 1 $)
Ток и напряжение синфазны. Вся энергия передается в нагрузку. Реактивной мощности нет.

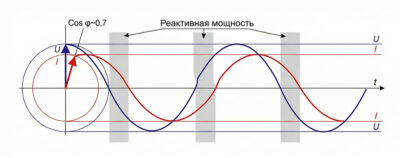
Осциллограмма тока, напряжения и реактивной мощности в сети при Cos Phi = 0.7

Вариант Б: Норма ($ \cos \varphi \approx 0.7 $)
Появляется сдвиг фаз. Обратите внимание на серые зоны — это периоды, когда ток и напряжение имеют разные знаки.

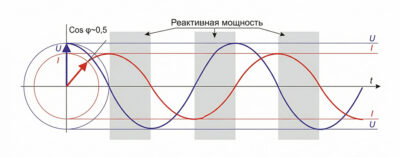
Осциллограмма тока, напряжения и реактивной мощности в сети при Cos Phi = 0.5

Вариант В: Плохо ($ \cos \varphi \approx 0.5 $)
Огромные серые зоны. Половину времени энергия течет от источника к нагрузке, а вторую половину — возвращается обратно.

Серые зоны на графиках Б и В — это визуализация возврата энергии. В эти моменты мгновенная мощность $ p(t) = u(t) \cdot i(t) $ становится отрицательной. Энергия «плещется» в проводах туда-сюда, нагревая их, но не выполняя работу. Это и есть реактивная мощность.

p(t) = \underbrace{\frac{V_m I_m}{2} \cos \phi \cdot (1 + \cos 2\omega t)}_{\text{Активный поток}} + \underbrace{\frac{V_m I_m}{2} \sin \phi \cdot \sin 2\omega t}_{\text{Реактивный поток (серые зоны)}}

Аналогия для понимания: Представьте, что вы толкаете тяжелую вагонетку (нагрузка).

Активная мощность (P): Это ваши усилия, направленные строго вперед, по рельсам. Вагонетка едет, работа совершается.

Реактивная мощность (Q): Представьте, что вы толкаете вагонетку под углом, упираясь плечом в бок. Часть ваших сил уходит на то, чтобы раскачивать вагонетку из стороны в сторону (вжимать её в рельс). Эта энергия не двигает вагонетку вперед, но вы все равно тратите силы (греетесь), и рельсы изнашиваются.

2. Математическая модель: Треугольник мощностей

Для инженерных расчетов мы используем векторное представление. Соотношение между активной ($ P $), реактивной ($ Q $) и полной ($ S $ или $ A $) мощностью описывается теоремой Пифагора.

$$A = \sqrt{P^2 + Q^2}$$

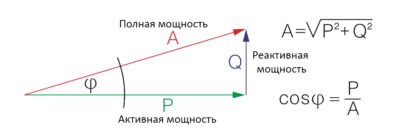
Треугольник мощностей и формула косинуса фи

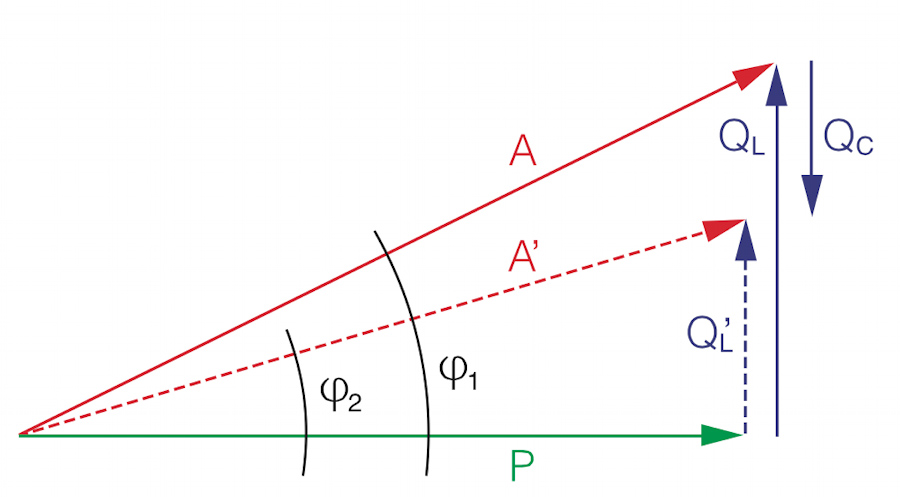
Рис. 1. Классический треугольник мощностей. Гипотенуза A всегда длиннее катета P, если угол φ отличен от нуля.

На диаграмме выше четко видно:

P (Зеленый вектор): Активная мощность, совершающая работу.
Q (Синий вектор): Реактивная мощность, «паразитная» нагрузка.
A (Красный вектор): Полная мощность. Именно на эту величину должны быть рассчитаны трансформаторы и кабели.

3. Две стороны коэффициента мощности: Displacement vs Distortion

Классическое определение $ \cos \phi $ (Power Factor) справедливо только для линейных нагрузок (ТЭНы, прямые пуски двигателей). В современных реалиях, насыщенных электроникой (ИБП, частотные преобразователи), необходимо разделять два понятия:

Коэффициент сдвига (Displacement Power Factor, DPF): Тот самый $ \cos \phi_1 $, учитывающий сдвиг фаз только основной гармоники (50 Гц). Корректируется конденсаторами.
Истинный коэффициент мощности (True Power Factor, $ \lambda $): Учитывает влияние высших гармоник тока.

\lambda = \frac{P}{S_{total}} = \frac{\text{DPF}}{\sqrt{1 + \text{THD}_I^2}}

Где $ \text{THD}_I $ — суммарный коэффициент гармонических искажений тока.

Замечание: Если вы установите конденсаторную установку (УКРМ) на вводе питания частотно-регулируемого привода, вы можете поднять $ \cos \phi $ до 1.0, но истинный коэффициент мощности останется низким из-за гармоник. Более того, конденсаторы могут перегреться и выйти из строя из-за высоких токов на частотах гармоник (150, 250, 350 Гц).

4. Нормативное регулирование в РФ: Приказ № 380

В Российской Федерации отношения между сетевыми организациями и потребителями в части реактивной мощности регулируются Приказом Минэнерго РФ от 23.06.2015 № 380. Важно отметить, что норматив устанавливается не для косинуса ($ \cos \phi $), а для тангенса ($ \tan \phi $), так как он линейно отражает соотношение $ Q/P $.

Таблица 1. Предельные значения коэффициента реактивной мощности ($ \tan \phi $)

Уровень напряжения	Нормативный $ \tan \phi $	Эквивалентный $ \cos \phi $	Комментарий
110 кВ и выше	0.50	0.89	Магистральные сети
35 кВ (60 кВ)	0.40	0.93	Субпередача
0.4 кВ (ниже 1 кВ)	0.35	0.94	Основной класс напряжения потребителей

Экономическая модель потерь

Прямых штрафов «за низкий косинус» в тарифах для большинства потребителей нет, однако существует обязательство оплачивать потери электроэнергии, возникшие из-за перетока реактивной мощности. Формула расчета дополнительных потерь ($ \Delta P $) выглядит следующим образом:

\Delta P = P_{fact} \cdot K_{loss} \cdot (\tan \phi_{fact} — \tan \phi_{norm})

Снижение $ \tan \phi $ с 1.0 (cos 0.7) до 0.35 (cos 0.94) позволяет не только избежать оплат за потери в адрес сетей, но и разгрузить собственный силовой трансформатор, позволив подключить до 30% новой активной нагрузки без замены подстанции (CAPEX).

5. Принцип компенсации: Векторная арифметика

5.1. Как работает конденсаторная установка

Суть компенсации — добавить вектор, направленный в противоположную сторону от индуктивной нагрузки. Конденсаторы генерируют ток, опережающий напряжение на 90°, что математически эквивалентно отрицательной реактивной мощности (или вектору, направленному вниз).

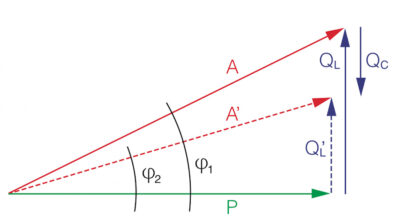
Рис. 2. Принцип компенсации. Добавление вектора Qc (конденсатор) уменьшает итоговый реактивный ток QL’ и сокращает полную мощность A’ (пунктирная линия).

Обратите внимание на Рис. 2: вектор $ A’ $ (новая полная мощность) стал значительно короче вектора $ A $, хотя полезная мощность $ P $ осталась неизменной. Это означает, что мы разгрузили трансформатор и уменьшили потери, просто добавив вектор $ Q_C $.

5.2. Расчет мощности установки

Требуемая мощность батареи $ Q_c $ рассчитывается как разница тангенсов углов $ \varphi_1 $ (до компенсации) и $ \varphi_2 $ (целевой):

Q_c = P \cdot (\tan \varphi_1 — \tan \varphi_2)

Внимание: Резонанс! Просто добавить конденсатор недостаточно. В сетях с гармониками (как на Рис. 2, где векторы идеальны) реальная картина сложнее. Конденсатор может войти в резонанс с индуктивностью сети. Обязательно используйте дроссели расстройки (Detuned Reactors) — 7% или 14%.

6. Технологии компенсации: От Пассивных к Активным

6.1. Конденсаторные установки (УКРМ) с расстройкой (Detuned)

Рис. 3. Конденсаторная установка (УКРМ).

Классические конденсаторы (KVAR) дешевы, но опасны в «грязных» сетях. Конденсатор и индуктивность трансформатора образуют последовательный колебательный контур с резонансной частотой:

f_{res} = f_{grid} \cdot \sqrt{\frac{S_{sc}}{Q_c}}

Для предотвращения резонанса используются дроссели расстройки (Detuned Reactors). Они сдвигают резонанс ниже частоты самой мощной гармоники.

Типовые коэффициенты расстройки (p):

p = 7% ($ f_{res} = 189 $ Гц): Самый популярный стандарт. Защищает от 5-й гармоники (250 Гц) и выше. Подходит для большинства промышленных предприятий.
p = 14% ($ f_{res} = 134 $ Гц): Используется при высоком уровне 3-й гармоники (150 Гц) — типично для офисных центров с однофазными нагрузками и освещением.
p = 5.67% ($ f_{res} = 210 $ Гц): Экономичный вариант, но ближе к опасной зоне 5-й гармоники.

6.2. Статические генераторы реактивной мощности (SVG / STATCOM)

SVG (Static Var Generator) — это революция в компенсации. Устройство представляет собой инвертор напряжения на IGBT-транзисторах. В отличие от конденсаторов, SVG не является пассивным элементом, а генерирует напряжение нужной фазы и амплитуды, формируя компенсирующий ток.

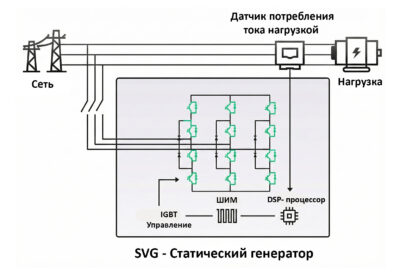
Схема Статического Генератора (SVG). Схема показывает IGBT-мосты, подключенные к сети. Контроллер измеряет ток нагрузки и мгновенно формирует противофазный ток.

Рис. 4. Принципиальная схема работы SVG: Цифровой процессор (DSP) анализирует ток нагрузки через датчик трансформатор тока (ТТ) и мгновенно формирует компенсирующий сигнал через IGBT-транзисторы.

Таблица 2. Сравнительный анализ: УКРМ vs SVG

Параметр	УКРМ (Конденсаторы + Дроссели)	SVG (Статический генератор)
Принцип работы	Ступенчатая коммутация емкости	Плавная генерация тока (Инвертор)
Время реакции	20 сек – 3 мин (время разряда)	< 10 мс (мгновенно)
Точность	Ступенчатая (грубая), возможна перекомпенсация	Плавная, удержание $ \cos \phi = 0.99 $
Работа с емкостью сети	Нет (может только генерировать Q)	Да (может потреблять Q, устраняя перенапряжения)
Резонанс	Возможен (требует тщательного расчета)	Исключен (SVG — источник тока)
Стоимость	Низкая	Высокая (в 2-3 раза дороже)

7. Методика расчета компенсации

Для подбора установки необходимо определить требуемую мощность $ Q_c $ (кВар). Базовая формула:

Q_c = P \cdot (\tan(\arccos(\cos \phi_1)) — \tan(\arccos(\cos \phi_2)))

Где:

$ P $ — Активная мощность нагрузки (кВт).
$ \cos \phi_1 $ — Фактический коэффициент мощности (до компенсации).
$ \cos \phi_2 $ — Целевой коэффициент мощности (обычно 0.95 — 0.98).

Практический пример: Завод потребляет 500 кВт с $ \cos \phi = 0.7 $. Цель: 0.96.
1. $ \tan \phi_1 $ (для 0.7) ≈ 1.02
2. $ \tan \phi_2 $ (для 0.96) ≈ 0.29
3. $ Q_c = 500 \cdot (1.02 — 0.29) = 365 $ кВар.
Выбираем стандартную установку 400 кВар с дросселями 7%.

8. Интересные факты о реактивной мощности

1. «Пена в пиве». Самая известная аналогия: Пиво — это активная мощность, пена — реактивная. Вы платите за полный бокал (Полная мощность S), но жажду утоляет только жидкость. Однако без пены (магнитного поля) пиво выдохнется (двигатель не запустится).
2. Кабель как генератор. Современные кабельные линии из сшитого полиэтилена (XLPE) 10-110 кВ обладают огромной емкостью. Ночью, на холостом ходу, они генерируют мегавары реактивной мощности, вызывая опасный рост напряжения в сети (Эффект Ферранти).
3. Влияние на пропускную способность. Повышение $ \cos \phi $ с 0.7 до 0.99 уменьшает ток в линии на 30%. Это позволяет передавать по тому же кабелю на 40% больше полезной активной мощности.
4. SVG для сварки. Обычные конденсаторы не успевают за сварочным роботом (сварка длится доли секунды). SVG реагирует за 5 мс, устраняя «мигание» света (фликер) в цеху.
5. Штрафы за «воздух». В некоторых странах Европы и Азии тариф за реактивную энергию может превышать тариф за активную, если превышен лимит. В России система работает через оплату потерь.
6. Гармоники убивают конденсаторы. Сопротивление конденсатора падает с ростом частоты ($ X_c = 1/2\pi fC $). Для 5-й гармоники (250 Гц) конденсатор становится почти коротким замыканием, вбирая в себя всю «грязь» из сети и взрываясь.
7. HVDC и ноль реактивки. Линии постоянного тока сверхвысокого напряжения не передают реактивную мощность. Это позволяет передавать энергию на тысячи километров без потерь на перемагничивание.

9. Часто задаваемые вопросы (FAQ)

1. Нужно ли ставить компенсацию в частном доме?

В 99% случаев — нет. Бытовые счетчики в РФ учитывают только активную энергию (кВт*ч). Вы не платите за реактивную мощность. Хотя установка маленького конденсатора может чуть разгрузить вашу проводку, экономически это не окупится никогда.

2. Почему установка греется и гудит?

Если гудят дроссели в УКРМ — это нормально (магнитострикция), но сильный перегрев может указывать на перегрузку гармониками. Если греются конденсаторы («бочонки») — это тревожный знак, возможно, они уже деградировали или работают в режиме резонанса. Требуется срочная проверка тепловизором.

3. Что такое перекомпенсация и чем она опасна?

Это ситуация, когда емкостной ток превышает индуктивный (сеть становится емкостной, $ Q < 0 $). Это вызывает повышение напряжения в сети выше номинала (например, 420В вместо 400В), что может сжечь электронику и привести к отключению вводных автоматов.

4. Можно ли использовать автомобильные конденсаторы для звука?

Категорически нет. Они рассчитаны на постоянный ток (DC) 12-24В. В сети переменного тока 230В они взорвутся мгновенно. Промышленные конденсаторы — это специальные устройства переменного тока (AC) с самовосстанавливающимся диэлектриком.

5. Где лучше ставить компенсацию: на ТП или у двигателей?

Индивидуальная (у двигателя): Лучшая технически. Разгружает кабель до самого мотора. Минус — дорого (много устройств).
Централизованная (на ТП): Дешевле всего. Убирает штрафы от сетей. Но кабели внутри цеха остаются загруженными реактивным током.
Гибридная: Оптимальный выбор. Мощные узлы компенсируем на месте, остальное «добираем» на вводе.

Заключение

Управление реактивной мощностью трансформировалось из простой задачи «экономии на счетах» в критический элемент надежности инфраструктуры. В современных условиях, когда сети насыщены нелинейной нагрузкой, применение устаревших решений (конденсаторов без дросселей) несет прямые риски аварий и пожаров.

Грамотный инженерный подход подразумевает обязательный аудит качества электроэнергии перед выбором оборудования, использование расстроенных фильтров (Detuned) как стандарта де-факто и переход на статические генераторы (SVG) там, где требуется быстродействие и высокая точность. Соблюдение требований ГОСТ 32144-2013 и Приказа № 380 — это не просто формальность, а гарантия долговечности дорогостоящего промышленного оборудования.

Нормативно-правовая база:

Приказ Минэнерго РФ от 23.06.2015 № 380 «О Порядке расчета значений соотношения потребления активной и реактивной мощности…».Устанавливает предельные значения $\tan \varphi$ (от 0.35 до 0.5).
ГОСТ 32144-2013 «Нормы качества электрической энергии в системах электроснабжения общего назначения».Определяет допустимые уровни гармоник и колебаний напряжения, что важно для выбора между УКРМ и SVG.
Правила устройства электроустановок (ПУЭ), 7-е издание (Глава 1.2. Электроснабжение и электрические сети). Базовые требования к надежности и выбору компенсирующих устройств.
ГОСТ IEC/TR 61000-3-6-2020 «Электромагнитная совместимость. Оценка норм эмиссии помех…». Норматив для оценки влияния «грязной» нагрузки (приводов, сварки) на общую сеть.

Список литературы

Железко Ю.С. Потери электроэнергии. Реактивная мощность. Качество электроэнергии. — М.: ЭНАС, 2009.
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2021.
Розанов Ю.К., Рябчицкий М.В. Силовая электроника. — М.: МЭИ, 2009.
Арриллага Дж., Брэдли Д. Гармоники в электрических системах. — М.: Энергоатомиздат, 1985.

Реактивная мощность и Косинус Фи cos(φ): теория, расчет и компенсация в сети